Particle Filter 알고리즘 기반 이산 웨이블릿 변환 기법의 경험적 모델 설계를 통한 리튬이온 배터리의 잔여 수명 예측
 ; Jinhyeong Park1)
; Jinhyeong Park1) ; Sanguk Kwon1)
; Sanguk Kwon1) ; Seunghwa Sin1)
; Seunghwa Sin1) ; Bumjong Kim2)
; Bumjong Kim2) ; Jonghoon Kim*, 1)
; Jonghoon Kim*, 1)
Copyright Ⓒ 2022 KSAE / 196-03
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
Electric vehicles(EVs) are being commercialized as practical alternatives to the Zero emission vehicle. Lithium-ion batteries(LIBs), the main source of energy for EVs, are one of the components that affect the economy and the safety of EVs due to LIB’s high energy density and long lifespan. However, LIBs can be problematic in terms of fading capacity and reduced life due to prolonged charging/discharging. Therefore, accurate remaining-useful-life(RUL) prediction is essential. In this paper, the discharge capacity of the lithium-polymer battery pack and the nickel manganese cobalt(NMC) battery were extracted through current signals. By using discrete wavelet transform(DWT), it is possible to induce capacity regeneration, such as the noise of the NMC battery, by compression and decomposition. To provide accurate batteries’ replacement time, RUL is implemented based on particle filter(PF). The result shows that the RUL prediction of the decomposed signals with noise improved by about 5% compared to the raw signal data. Therefore, in this paper, it was proposed that using decomposed signals can be an advantage in terms of data storage space and the effect of reduced RUL time.
Keywords:
Electric vehicle, Lithium-ion battery, Discrete wavelet transform, Particle filter algorithm, Remaining-useful-life prediction키워드:
전기 자동차, 리튬이온 배터리, 이산 웨이블릿 변환, 입자 필터 알고리즘, 잔여 수명 예측1. 서 론
최근 지구온난화 같은 환경 문제에 대한 대안책으로 내연기관을 대신한 전기자동차(Electric Vehicle; EV)에 대한 정책 및 규제들이 강화되고 있다. 전기자동차 구매를 지원하는 정부 정책 및 규제가 향후 전기자동차 판매량을 촉진할 전망이며, 이는 저탄소 배출 차량 구매 시 보조금 지원, 전기차 금전적 인센티브 지원 등에서 알 수 있다.1) 또한, 전기차 확대는 2015년에 체결된 파리 협약, 2021년 유럽에서 시행 예정인 이산화탄소 배출 감소 조치와 같이 기후 변화에 대응하기 위한 필수적 대안 중 하나로 자리잡았다.2) 이러한 전기자동차의 에너지원으로 리튬이온 배터리(Lithium-Ion Battery; LIB)가 많이 사용되고 있다. LIB는 친환경 에너지원이며, 고출력, 긴 수명, 높은 에너지 밀도 등의 장점으로 인해 온실가스 감축에 대한 대안책이 되었다. 이에 따라, LIB를 사용하는 전기자동차의 수용성 제고에 대한 주행거리 향상 목적을 이루기 위해 고용량의 배터리가 요구되고 있다. 이러한 대용량의 LIB를 관리하기 위해 배터리 관리 시스템(Battery Management System; BMS)이 필수적이다. 하지만, 대용량 전기자동차가 증가하면서 상용 중에 있는 BMS는 취득 가능한 데이터의 저장 용량이 부족하며, 수명 예측을 위한 물리적인 계산 능력의 한계점에 도달하였다.3)
이러한 BMS의 한계성과 대용량 시스템의 증가 및 신뢰성 문제의 해결책으로 수명 예측 및 관리기술(Prognostics and Health Management; PHM) 연구가 대두되고 있다.3) 수명 예측 및 관리기술은 배터리의 상태를 추정하고 현재 상태를 기반으로 미래의 상태를 예측한다. 또한, 데이터 측정, 건전성 지표 추출, 수명 상태 추정, 잔여 수명 예측으로 크게 나눌 수 있다. PHM의 목적은 시스템의 안정적인 제어 및 관리, 배터리의 유지 보수에 있다. 이에 따라 BMS의 안전 및 신뢰성에 크게 기여한다.4) PHM의 주요 연구는 배터리 충전 상태(State-of-Charge; SOC) 및(State-of-Health; SOH) 추정, 잔여 수명(Remaining-Useful-Life; RUL) 예측 등이 있다. 본 논문에서는 측정된 전류 데이터를 통해 방전 용량을 이산 시간에 표현하여 RUL을 진행한다.
전기자동차 장시간 운행 및 잦은 충전으로 인해 수명과 성능은 악화된다. 이는 용량 감소와 저항 증가와 같은 열화 형태로 나타난다. 따라서, 배터리 용량 감소에 대한 예측은 필수적이며, 전기자동차의 안전성 및 신뢰성에 기여할 수 있다. 구체적으로, 배터리 RUL 예측은 배터리가 초기 용량 대비 20 % 감소한 EOL(End-of-Life)까지의 도달 시간으로 정의된다. 대표적으로 RUL 예측의 방법은 데이터 기반(Data-driven), 모델 기반(Model-based), 적응형 제어 기반(Adaptive filter-based) 방식들로 분류할 수 있다.5) 이 중 데이터 기반의 방법 같은 경우 예측 성능은 오직 Train 데이터에 의존하기 때문에 다양한 온도 및 환경 조건에서 정확성을 보장하지 못한다.6) 모델 기반 방법 같은 경우 모델 파라미터를 통해 배터리의 열화 현상을 예측한다. 하지만, 배터리의 비선형적 용량 특성과 Non-Gaussian 노이즈에 대해 정확하지 않은 예측 성능을 보인다.7) 또한, 대용량의 데이터 수급이 필요한 단점이 존재한다. 이러한 개선점을 보완하기 위해 비선형 및 Non-Gaussian 노이즈의 상태 추정 및 예측에 적합한 Particle Filter(PF)가 주로 사용된다.5) PF 알고리즘의 특징은 배터리가 열화 되며 발생하는 용량 감소의 경향을 경험적 모델 설계를 통해 잔여 수명 예측을 진행한다. 따라서 정확한 용량 추정의 경험적 모델 설계가 필수적이다.
본 논문에서는 모델 설계를 위해 사용한 배터리는 리튬 폴리머(Lithium-polymer)와 양극재가 NCM(Nickel Cobalt Manganese) 계열인 배터리이다. NCM 배터리의 경우 Cycle이 진행됨에 따라 용량이 회복하는 현상이 발생한다. 이는 정확하지 않는 용량 정보이며, 경험적 모델 설계 시 잔여 수명 예측의 성능을 떨어뜨린다. 또한, 이러한 현상은 전기자동차 사용자의 성향에 따라 휴지 시간 및 외부 환경에 따라 발생할 수 있다. 따라서, 본 논문에서는 시간-주파수에 따라 신호를 분석하여 분해하는 이산 웨이블릿 변환(Discrete Wavelet Transform; DWT) 기법을 사용하였다.8) DWT 기법에서 배터리 용량의 회복 현상을 신호로 입력 받아 노이즈 현상을 제거한 데이터의 추출을 하였다. 출력 데이터를 통해 경험적 모델의 설계를 하여 잔여 수명 예측을 진행하였다. 또한, DWT 사용 시 저주파 필터에 의해 데이터를 압축 및 분해를 할 수 있다. 이를 통해 향후 다량의 셀로 구성된 배터리 팩 구성 시 취득 데이터에 대한 압축을 통해 BMS의 저장 공간의 한계성도 해결할 수 있다.
본 논문에서는 LIB의 잔여 수명 예측을 진행하기 위해 방전 용량 데이터를 각 사이클 별로 추출하였다. 이를 DWT 기법을 활용하여 데이터의 압축 및 분해를 진행하여 경험적 모델 설계를 진행하였다. 그리고 PF 알고리즘 기반 잔여 수명 예측을 배터리 종류 및 분해 데이터에 따라 정확도 비교를 진행하였다.
2장에서는 전기적 특성 실험과 방전 용량 데이터에 대한 설명을 진행한다. 3장에서는 DWT 기법에 대한 설명과 데이터의 압축 및 분해에 대한 설명을 진행한다. 4장에서는 PF 알고리즘 기반 잔여 수명 예측 정확도의 비교 분석을 진행한다. 마지막으로 연구한 주제에 대한 결론을 5장에 기술한다.
2. 배터리 전기적 특성 실험
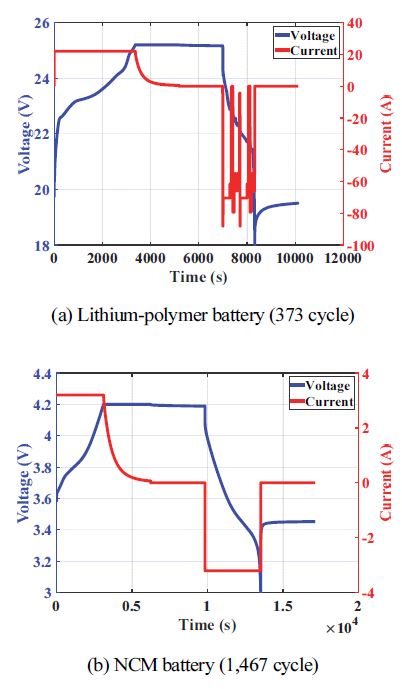
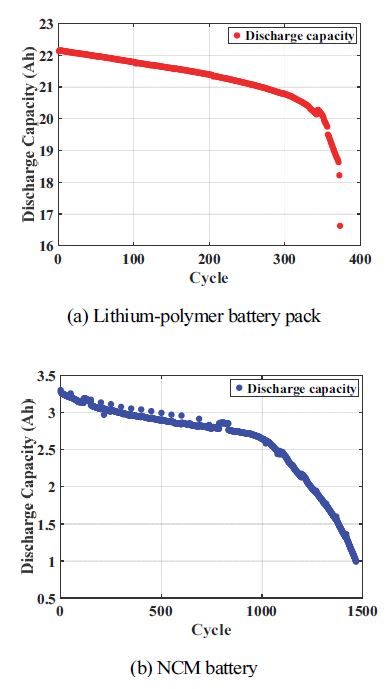
본 논문에서 사용한 배터리는 리튬 폴리머와 양극 소재가 NCM 계열인 배터리를 사용하였다. 리튬 폴리머 배터리 같은 경우 6개의 셀이 직렬로 구성된 22 Ah 팩이며, 양극 소재가 NMC 계열인 배터리는 INR 21700-33J 배터리이다. Table 1은 본 논문에서 사용한 배터리의 사양이다. 배터리 용량 감소에 대한 온도 조건의 영향성을 줄이고자 프로파일 및 열화 실험은 항온 챔버를 25 oC 조건에서 진행하였다.9) 리튬 폴리머 배터리는 용량 실험과 전기 자동차의 주행 환경을 묘사하기 위한 프로파일 실험을 진행하였다. 용량 실험은 0.2 C-rate(4.4 A)의 전류로 충/방전을 2번 반복하였으며, 휴지 시간을 30분으로 설정하였다. 프로파일 실험의 경우 정전류-정전압(Constant Current-Constant Voltage; CC-CV) 방식으로 충전하였고, 방전 시 가변적 조건의 전류를 설정하여 진행하였다. 이는 전기자동차의 속도가 변하는 상황을 묘사한 프로파일이다. 프로파일 방전 조건의 경우 총 13단계로 구성되어 있으며, Table 2에 표시하였다. 실험에 사용된 프로파일의 경우 Fig. 1(a)에 표시하였다. Fig. 2(a)에 각 사이클 별 방전 용량을 추출하였으며, 330 cycle 부근에서 용량이 급격이 감소하는 Knee point를 확인하였다.10) NMC 배터리의 경우 1C-rate(3.3 A)의 전류로 만충과 만방을 진행하였으며, 1,464 cycle의 열화 실험을 수행하였다. 그 결과 1,004 cycle에서 EOL에 도달하였다. Fig. 1(b)는 NMC 배터리의 충/방전 그래프이며, Fig. 2(b)는 각 사이클 별 방전 용량 그래프이다. NMC 배터리 방전 용량의 경우 용량 회복 현상이 700 cycle까지 발생하는 것을 확인할 수 있다. 이는 실험 과정 중 일정하지 않은 배터리 휴지 시간으로 인해 배터리의 비선형성이 심화되는 결과이다. 본 논문에서 이를 노이즈로 가정하고 3 장에서 소개할 이산 웨이블릿 변환 기법을 사용하여 노이즈를 감쇄하여 용량을 출력하였다.
3. 이산 웨이블릿 변환
3.1 이산 웨이블릿 변환 기법
웨이블릿 분석(Wavelet analysis)은 시간과 주파수에 관한 해석 기법으로 입력 신호에 따라 다른 Window의 영역을 설정하여 다해상도(Multi resolution) 분석을 한다. 이는 정지상태가 아닌 신호의 경우 푸리에(Fourier) 분석의 시간 정보가 손실되는 신호를 주파수 영역으로 변환하는 단점을 보완한다.11) 이러한 단점을 보완하기 위해 단시간 푸리에 변환(Short-time Fourier Transform; SFET)의 한 번에 신호의 작은 부분 즉, Window 설정을 분석할 수 있다. 하지만, 모든 주파수에 대해 시간 Window의 크기가 동일하다는 단점이 존재하여 웨이블릿 분석 기법을 사용하는 것이 효율적이다.12) 웨이블릿 변환은 다양한 시간과 주파수 영역에 대한 Window 크기를 원하는 신호에 부합하게 설정할 수 있다. 웨이블릿 변환 중 DWT는 연속시간으로 데이터를 처리하는 연속 웨이블릿 변환(Continuous Wavelet Transform; CWT)에 비해 연산량을 효과적으로 줄여 배터리 상태를 예측하는데 효율적이다. 또한, 배터리의 방전 용량 데이터의 경우 이산 시간의 데이터이기 때문에 본 논문에서는 DWT 기법을 사용하였다. 식 (1)은 DWT의 정의식이다.13)
| (1) |
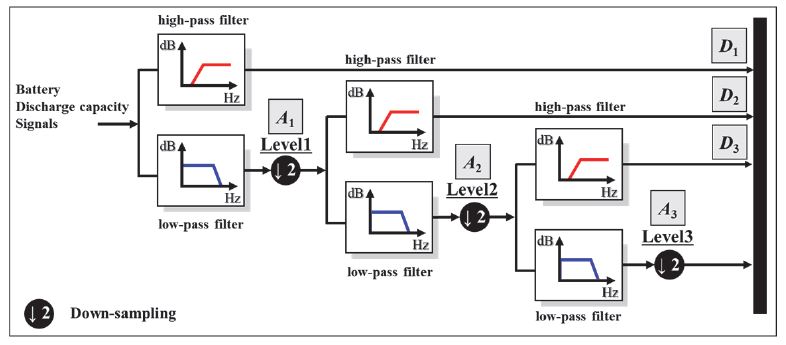
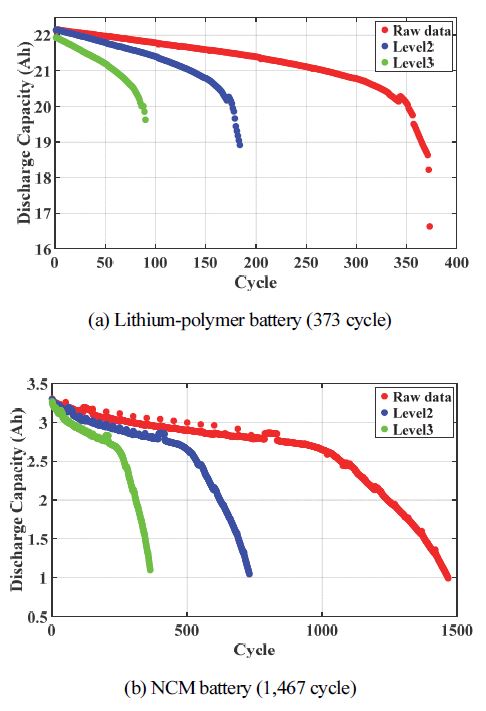
여기서 j, k는 켤레 복소수이고, Y(t)는 DWT에 의해 분해된 신호이며, j는 분해 Level이다. 본 논문에서 사용된 Level 수는 Level 3까지 사용하였다. ϕ(t)는 크기를 나타내는 함수이며, ψ(t)는 웨이블릿 함수이다. 이는 DWT의 모함수가 Window의 크기에 따라 변하도록 한다. 본 논문에서 사용한 모함수는 Daubechies를 사용하였다.14) 또한, hj(n)과 lj(n)은 각각 High-pass filter와 Low-pass filter이다. 본 논문에서는 배터리 방전 용량의 데이터의 압축과 분해를 위해 저주파 신호만 사용하였다. 또한, 전기자동차용 배터리의 경우 저주파 영역대의 운용 환경에서 동작한다. Fig. 3은 DWT를 사용하여 Level 3까지 배터리의 방전 용량 신호를 분해한 구조도이다. 데이터의 압축과 변환을 위해 Fig. 4와 같이 각 사이클 및 Level 별로 방전 용량 그래프를 출력하였다. 그 결과 리튬 폴리머 배터리 팩과 같은 경우 373개의 데이터가 Level 2에서 184개, Level 3에서 90개로 분해되는 것을 확인하였다. 또한, 원 신호의 특성 상 회복 현상이 발생하지 않아 노이즈에 대한 성분이 거의 존재하지 않았다. NMC 배터리와 같은 경우 1,467개의 데이터가 Level 2에서 731개, Level 3에서 364개로 분해되었다. 또한, NCM 배터리의 경우 일정하지 않은 휴지 시간으로 인해 용량 회복 현상이 일어나 노이즈 현상이 발생하였다. DWT를 사용한 결과 Level이 높아질수록 노이즈 현상이 줄어드는 것을 확인할 수 있었다. 이를 통해 원 신호 및 분해된 신호를 MATLAB 환경에서의 Fitting을 통해 모델을 생성하여 4 장에서 소개할 잔여 수명 예측을 진행하였다.
4. Particle Filter 알고리즘 기반 잔여 수명 예측
4.1 Particle Filter 알고리즘
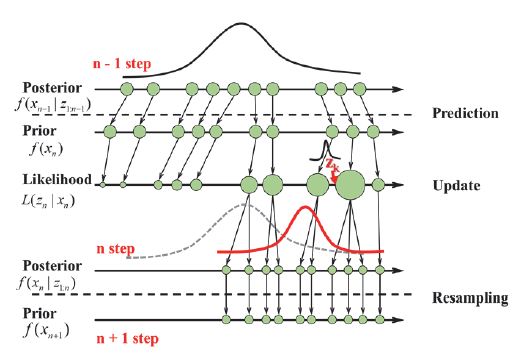
PF 방법은 몬테카를로(Monte Carlo) 시뮬레이션 방법을 사용하여 상태를 추정하는 알고리즘이다. PF 알고리즘은 확률론을 기반으로 연속된 상태를 갖는 경우에 시간의 흐름에 대해 재귀적으로 베이지안(Bayesian) 추정을 사용한다.15) 이는 가중치를 갖는 Particle 샘플 세트의 확률 밀도 함수(Probability Density Function; PDF)로 추정치를 예측한다. Fig. 5와 같이 PF 알고리즘은 예측(Prediction), 업데이트(Update), 재 생성(Resampling)의 단계로 구성되어 있다. 예측 단계에서 Posterior 확률 분포 기반 추정된 경험적 모델을 통하여 예측 값(Prior)을 추출한다. 업데이트 단계에서는 예측 값 확률 분포에 실제 값(zk)이 존재할 확률을 통해 가능도(Likelihood)함수를 업데이트한다. 또한, 업데이트 시 확률이 높은 Particle은 높은 가중치를 갖고, 확률이 낮은 Particle은 적은 가중치를 갖는다. 마지막은 재 생성 단계로 업데이트된 가능도 함수에서 Particle 샘플을 추출하며, 가중치가 적은 Particle은 사라진다. Table 3의 수식과 같이 세 가지 단계를 반복하며 진행된다. PF 알고리즘에서 배터리 방전 상태를 나타내는 상태 방정식이 사용되며, 식 (2)와 (3)과 같이 정의한다.16)
| (2) |
| (3) |
여기서 n은 cycle, xn은 배터리의 방전 상태, zn은 방전 용량 측정 값, vn은 PF 알고리즘의 자체 노이즈, wn은 측정 노이즈를 나타낸다. 본 논문에서는 PF 알고리즘의 자체 노이즈, 측정 노이즈의 영향을 배제한다. f(·)는 배터리 방전 상태를 나타내는 모델을 포함하는 상태 전이 함수이며, h(·)는 측정 함수를 나타낸다. 본 논문은 초기 Particle 개수를 5,000개로 설정하였고, 신뢰도 구간(Confidence Interval; CI)을 95 %로 설정하여 잔여 수명 예측을 진행하였다.
4.2 이산 웨이블릿 변환 기반 경험적 모델 설계
3장에서 소개한 DWT 저주파 기반 변환을 통해 리튬 폴리머 배터리 팩, NCM 배터리의 방전 용량 데이터를 Level 2, Level 3 분해로 출력하였다. 리튬 폴리머 배터리 팩의 경우 373 cycle의 데이터를 184, 90의 데이터로 각각 분해하였다. 또한, NCM 배터리의 경우 1,467 cycle의 데이터를 731, 364의 데이터로 각각 분해하였다. PF 알고리즘의 경우 예측 단계에서 Posterior 기반 Prior의 PDF를 예측한다. 이 과정에서 경험적 모델의 배터리 비선형적 열화 패턴 반영이 필수적이며, 잔여 수명 예측 진행 시 추정성능을 결정짓는다. 경험적 모델의 경우 배터리의 열화 패턴을 근사한 모델이다. 따라서, 열화에 따른 비선형적 특성을 반영할 수 있어 정확성이 우수하며, 적은 데이터에서 알고리즘 구동이 가능하기 때문에 계산 능력이 우수하다. 본 논문에서는 2차 지수함수 모델을 사용하여 배터리의 방전 용량 데이터를 근사하였다. 식 (4)는 2차 지수함수 모델이다.5) 배터리 방전 시 용량 거동 특성은 전기적 특성 실험 기반으로 분석하였으며, 용량이 선형적으로 감소 중 Knee point를 넘어서면 급격하게 감소하는 2 단계로 나뉘는 것을 확인하였다.17) 이러한 배터리의 특성을 2차 지수함수 모델을 적용할 시 높은 정확도로 추정한다.18)
| (4) |
where a, b, c, d: Model coefficients(95 % CI)
4.3 잔여 수명 예측 결과
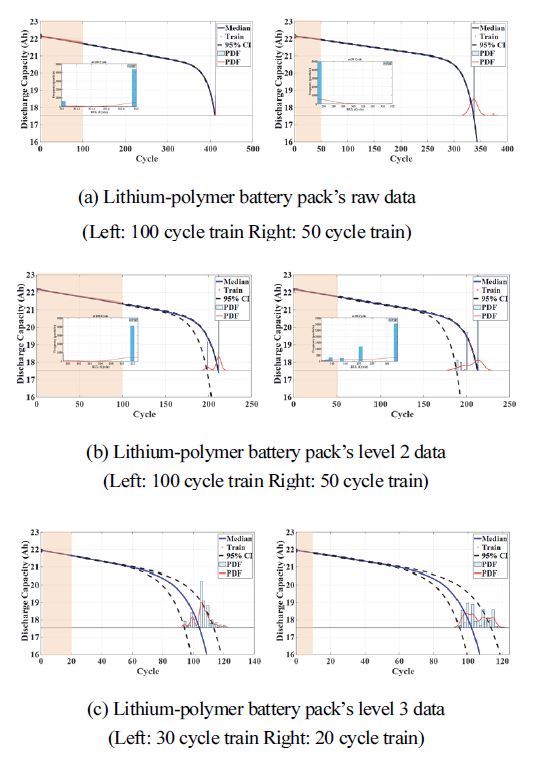
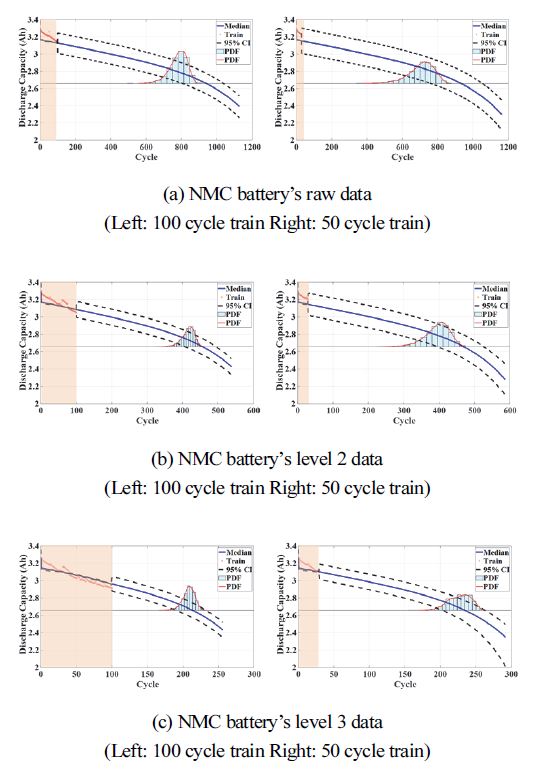
4.2절에서 소개한 2차 지수함수 모델을 사용하여 잔여 수명 예측을 PF 알고리즘 기반으로 진행하였다. Fig. 6과 7은 PF 알고리즘으로 잔여 수명을 예측한 그래프이다. 잔여 수명 예측 결과를 확률 밀도 함수로 표현하였으며, 95 % CI의 추정성능을 보였다. Median의 CI의 50 %를 의미하며, Train은 zk의 측정 데이터 값을 의미한다. Fig. 6과 7의 (a~c)는 각각 원 신호, Level 2 분해, Level 3 분해 데이터에 Train 데이터의 구성을 다르게 하여 잔여 수명 예측을 진행한 그래프이다. Table 4와 5는 잔여 수명 예측 결과를 나타낸 표이다. 리튬 폴리머 배터리의 EOL 도달 지점은 372 cycle이며, NCM 배터리의 EOL 도달 지점은 1,004 cycle이다. 또한, Level 2 데이터 같은 경우 원 신호로의 복귀를 위해 분해 신호에 2배 조건을 설정하였으며, Level 3 데이터 같은 경우 원 신호에 4배 조건을 설정하였다. 예측 결과 리튬 폴리머 배터리 팩은 원 신호와 분해된 데이터의 정확도 차이가 2 % 내외라는 것을 확인하였다. 이는 배터리의 방전 용량에 회복 현상과 같은 노이즈 현상이 없으면, 향후 배터리 팩의 용량 증가 시 데이터의 압축으로 활용한다. NCM 배터리는 원 신호와 분해된 신호들을 비교 시 Level 2, 3 데이터에서 100 cycle Train한 데이터의 추정 성능이 원 신호의 추정 성능보다 정확도가 5 % 증가한 것을 확인할 수 있었다. 이는 배터리 방전 시 용량 회복과 같은 노이즈 현상 발생 시 노이즈를 감쇄하여 예측 성능 향상 및 데이터 압축에서 우수한 결과이다.
5. 결 론
본 논문은 노이즈 현상이 발생하는 데이터를 DWT 기법으로 분해하여 잔여 수명 예측 정확도를 향상시키는 알고리즘을 제안하였다. 제안된 알고리즘은 BMS 대용량 데이터 취급 시, 노이즈 현상과 같은 성능을 저하시키는 요인을 제거할 수 있다. 또한, 데이터 분해를 통해 데이터의 메모리를 줄여 BMS 저장 공간의 효용성을 증가시킬 수 있다. 그 결과, 용량 회복과 같은 노이즈 현상이 발생하는 NMC 배터리의 데이터를 분해하였을 때, 원 신호 데이터보다 잔여 수명 예측 정확도가 5 % 증가하였다. 이는 DWT 기법을 활용한 데이터 분해와 PF 알고리즘 기반 잔여 수명 예측을 통해 확인할 수 있었다. 향후 제안된 알고리즘을 전기자동차 BMS 탑재 시, 배터리의 이력을 나타낼 수 있는 방전 용량 데이터의 확보가 필수적이며, 메모리 처리 속도 등을 고려하여 실시간으로 잔여 수명을 예측하는 연구를 진행할 것이다.
Nomenclature
| EV : | electric vehicle |
| BMS : | battery management system |
| NMC : | nickel cobalt manganese |
| STFT : | shor-time fourier transform |
| CWT : | continuous wavelet transform |
| DWT : | discrete wavelet transform |
| PF : | particle filter |
| RUL : | remaining-useful-life |
| PDF : | probability density function |
| CI : | confidence interval |
| j, k : | complex conjugate |
| Y(t) : | denoising DWT signals |
| ϕ(t) : | scaling function of the signal |
| ψ(t) : | wavelet function of the signal |
| hj(n) : | high-pass filter |
| lj(n) : | low-pass filter |
| An : | approximation component |
| Dn : | detail component |
| xn : | battery discharge capacity at time n |
| zn : | measurement value at time n |
| vn : | measurement noise sequence |
| wn : | process noise sequence |
Acknowledgments
A part of this paper was presented at the KSAE 2021 Spring Conference
이 연구는 한국전력공사의 2019년 선정 기초연구개발과제(‘R19XO01-45’) 및 산업통상자원부(MOTIE)와 산업기술평가관리원(KEIT) (No.20011626)의 지원을 받아 수행한 연구과제입니다.
References
- R. Smokers, R. Vermeulen, R. Van, R. Gense, I. Skinner, M. Fergusson, E. B Mackay, P. T. Brink, G. Fontaras and Z. Samaras, “Review and Analysis of the Reduction Potential and Costs of Technological and other Measures to Reduce CO2-emissions from Passenger Cars,” TNO, IEEP and LAT on Behalf of the European Commission (DG-ENTR), 2006.
-
R. S. Dimitrov, “The Paris Agreement on Climate Change: Behind Closed Doors,” Global Environmental Politics, Vol.16, No.3, pp.1-11, 2016.
[https://doi.org/10.1162/GLEP_a_00361]

- S. Kwon, K. Kim, S. Yoon, C. Lim and J. Kim, “A Study on the Multiple Health Monitoring Indicator for Remaining useful Life Prediction of Battery,” Proceedings of the KIPE Conference, Vol.4, pp.130-132, 2020.
-
H. Meng and Y. -F. Li, “A Review on Prognostics and Health Management (PHM) Methods of Lithium-ion Batteries,” Renewable and Sustainable Energy Reviews, Vol.116, pp.109405, 2019.
[https://doi.org/10.1016/j.rser.2019.109405]

-
L. Li, A. A. F. Saldivar, Y. Bai and Y. Li, “Battery Remaining useful Life Prediction with Inheritance Particle Filtering,” Energies, Vol.12, No.14, p.2784, 2019.
[https://doi.org/10.3390/en12142784]

-
D. Liu, X. Yin, Y. Song, W. Liu and Y. Peng, “An On-line State of Health Estimation of Lithium-ion Battery using Unscented Particle Filter,” IEEE Access, Vol.6, pp.40990-41001, 2018.
[https://doi.org/10.1109/ACCESS.2018.2854224]

-
J. Kim and B. H. Cho, “State-of-charge Estimation and State-of-Health Prediction of a Li-ion Degraded Battery Based on an EKF Combined with a Per-unit System,” IEEE Transactions on Vehicular Technology, Vol.60, No.9, pp.4249-4260, 2011.
[https://doi.org/10.1109/TVT.2011.2168987]

-
J. Kim, “Discrete Wavelet Transform- based Feature Extraction of Experimental Voltage Signal for Li-ion Cell Consistency,” IEEE Transactions on Vehicular Technology, Vol.65, No.3, pp.1150-1161, 2015.
[https://doi.org/10.1109/TVT.2015.2414936]

-
F. Leng, C. M. Tan and M. Pecht, “Effect of Temperature on the aging Rate of Li Ion Battery Operating above Room Temperature,” Scientific Reports, Vol.5, No.1, pp.1-12, 2015.
[https://doi.org/10.1038/srep12967]

-
W. Diao, S. Saxena, B. Han and M. Pecht, “Algorithm to Determine the Knee Point on Capacity Fade Curves of Lithium-ion Cells,” Energies, Vol.12, No.15, p.2910, 2019.
[https://doi.org/10.3390/en12152910]

- D. Min, H. J. Lee, K. Hur and S. J. Kim, “Noise Reduction in PMU Data Using Discrete Wavelet Transforms,” Proceedings of the 44th KIEE Summer Conference, pp.317-318, 2013.
-
S. Lee and J. Kim, “Discrete Wavelet Transform-based Denoising Technique for Advanced State-of-charge Estimator of a Lithium-ion Battery in Electric Vehicles,” Energy, Vol.83, pp.462-473, 2015.
[https://doi.org/10.1016/j.energy.2015.02.046]

-
C. Vonesch, T. Blu and M. Unser, “Generalized Daubechies Wavelet Families,” IEEE Transactions on Signal Processing, Vol.55, No.9, pp.4415-4429, 2007.
[https://doi.org/10.1109/TSP.2007.896255]

-
J. Xu, X. Mei, X. Wang, Y. Fu, Y. Zhao and J. Wang, “A Relative State of Health Estimation Method Based on Wavelet Analysis for Lithium-ion Battery Cells,” IEEE Transactions on Industrial Electronics, Vol.68, No.8, pp.6973-6981, 2020.
[https://doi.org/10.1109/TIE.2020.3001836]

-
F. Yang, D. Wanga, Y. Xing and K. L. Tsui, “Prognostics of Li(NiMnCo) O2-based Lithium-ion Batteries using a Novel Battery Degradation Model,” Microelectronics Reliability, Vol.70, pp.70-78, 2017.
[https://doi.org/10.1016/j.microrel.2017.02.002]

-
M. Jouin, R. Gouriveau, D. Hissel, M. C. Péra and N. Zerhouni, “Particle Filter-based Prognostics: Review, Discussion and Perspectives,” Mechanical Systems and Signal Processing, Vol.72, pp.2-31, 2016.
[https://doi.org/10.1016/j.ymssp.2015.11.008]

-
Y. Xing, E. W. M. Ma, K. L. Tsui and M. Pecht, “An Ensemble Model for Predicting the Remaining Useful Performance of Lithium-ion Batteries,” Microelectronics Reliability, Vol.53, No.6, pp.811-820, 2013.
[https://doi.org/10.1016/j.microrel.2012.12.003]

- J. Kim, J. Park and J. Kim, “Remaining Useful Life Prediction Based on Particle Filter Algorithm for Real-time Life Diagnosis of Electric Vehicle Battery,” KSAE Spring Conference Proceedings, p.818, 2021.