Data-Driven 차량 횡방향 모델 정확도 개선

1. 서 론

자동차 산업이 발전함에 따라 운전자의 편의와 안전에 대한 소비자의 요구가 증대되고 있다. 이러한 요구들을 충족시키기 위해 완성차 회사에서는 새로운 차량 제어 기술들을 개발하고 양산에 적용하고 있다. 최근 카메라, 레이더, 라이다 등 환경 센서의 장착률이 증가하면서 ADAS(Advanced Driver Assistant System)과 자율 주행 기술들이 비약적으로 실차에 적용되고 있으며, 이와 동시에 차량의 거동을 정확하고 견실하게 제어하기 위한 수학적 차량 모델에 기반한 다양한 제어 방법론들이 제안되고 있다.^1-3) 이렇게 차량 거동 제어에 대한 기능들이 발전하고 증대됨에 따라 정확한 주행 상황 판단과 제어는 매우 중요한 요소라 할 수 있다. 주행 상황 판단에는 주로 기준 차량모델을 기반으로 설계된 차량 상태 추정기가 이용되고, 판단에 따른 제어를 위해서는 기준 모델을 기반으로 하는 다양한 제어 방법론들이 사용된다. 따라서 여기에 사용되는 제어 관점의 차량 횡방향 모델의 성능은 주행 상황 판단과 제어에 있어 매우 중요한 역할을 한다.

차량의 횡방향 제어를 위해 많은 연구들이 2자유도 Single track 모델(또는 Bicycle 모델)을 기준 모델(Reference model)이 사용하고 있다.^1-3)

Single track 모델은 타이어의 특성을 선형으로 가정하여 도출된 매우 단순한 모델로 차량 거동 제어에 널리 사용되지만, 이러한 단순성으로 인해 모델 정확도가 보장되는 영역은 상당히 제한적이다. 따라서 Single track 모델의 정확도 개선은 차량 제어에 매우 중요한 연구라 할 수 있다. 하지만 Single track 모델의 오차를 분석한 연구나, 실차 수준에서 이를 분석하여 모델 정확도를 개선한 연구들은 매우 미비한 실정이다.^4-6) 대부분의 연구들은 모델 정확도 개선을 위해 선형 타이어 모델이 아닌 비선형 타이어 모델을 사용하였다.¹⁾ 하지만, 비선형 타이어 모델을 사용할 경우 모델의 정확도는 개선되는 반면, 모델의 복잡도가 증가되어 모델 예측 제어와 같은 최적화 기반의 제어 방식을 적용할 경우, 연산 효율이 떨어지게 된다.

본 논문에서는 실차 시험을 통해 계측된 데이터를 이용해 모델 오차 요인을 보상하여, 기존 Single track 모델의 단순성을 유지하면서도 정확도가 향상된 차량 횡 방향 모델을 개발하고자 한다. 모델 오차 요인으로는 크게 조향각과 코너링 강성이 있다. Single track 모델의 입력인 타이어 조향각의 경우 운전자의 조향휠 조작에 의해 결정되지만, 차량 전륜 서스펜션의 지오메트리 구조로 인해 발생하는 롤/컴플라이언스 조향의 영향을 받는다. 이러한 영향으로 발생되는 타이어 조향각 오차를 보상하기위해 기존 문헌에서는 횡 가속도 신호를 사용하였고, 개선된 타이어 조향각을 사용하는 경우 차량 횡 방향 모델의 정확도가 일부 향상됨을 확인하였다.^5,6) 하지만, 정확한 타이어 조향각을 알기 위해서는 별도의 조향각 측정 장비를 통해 계측한 실제 조향각과 비교하며 조향각 모델을 설계, 검증해야 하기 때문에 본 논문에서는 조향각보다는 코너링 강성의 정확도에 초점을 맞춰 연구를 진행하였다.

다양한 시나리오의 실차 시험에서 정밀 GPS/INS센서(RT3000)로 계측된 횡슬립각과 요레이트을 사용하여 코너링 강성의 오차를 보상하여 Single track 모델의 정확도 개선시키는 방안을 제안한다. Single track 모델은 전개 과정에서 타이어의 비선형적인 특성을 선형으로 가정하였기 때문에, 모델 오차의 가장 큰 원인은 코너링 강성의 부정확성이라 할 수 있다. 따라서 타이어의 비선형성이 고려된 코너링 강성을 사용할 경우 모델의 정확도는 크게 개선될 것이다. 이를 위해 코너링 강성을 고정 값이 아닌 최대 노면 마찰 계수로 정규화된 횡 가속도에 대한 비선형 Map으로 산출하는 방법을 제안하였고, 이 Map은 계측 데이터에 기반한 파라미터 최적화를 통해 도출하였다.

본 논문은 다음의 구조로 작성되었다. 2장에서 차량 횡 방향 모델 선정과 이에 대한 오차 분석을 실시하였고, 3장에서는 실차 계측 데이터를 사용한 파라미터 최적화 기반 코너링 강성 계수 오차 보상 방법을 상세 기술하였다. 4장에서는 제안한 모델 정확도 개선 방법을 실차 시험 데이터를 통해 검증하였으며 차량의 횡슬립각과 요레이트의 오차 개선을 분석하였다. 5장에서는 결론을 맺는 것으로 논문을 구성하였다.

2. 차량 횡 방향 모델 오차 요인 분석

2.1 차량 횡 방향 모델

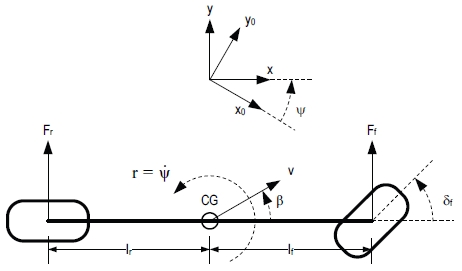
Single track 모델은 Planar motion을 가정하여 차량의 횡적 거동을 표현한 모델로 식 (1)과 같이 횡방향 힘 평형식과, 수직방향 모멘트 평형식으로 도출되며 차량의 횡슬립각(β)과 요레이트(r)에 대한 미분 방정식으로 나타낼 수 있다.

$\[ \begin{array}{c}\dot{\beta }=-r+\frac{C_f}{m{v}_x}\left({\delta }_f-\beta -\frac{l_f}{v_x}r\right)+\frac{C_r}{m{v}_x}\left({\delta }_r-\beta -\frac{l_r}{v_x}r\right)\hfill \\ \dot{r}=\frac{{l_{f}C}_f}{I_z}\left({\delta }_f-\beta -\frac{l_f}{v_x}r\right)-\frac{{l_{r}C}_r}{I_z}\left({\delta }_r-\beta +\frac{l_r}{v_x}r\right)\hfill \end{array} \]$

(1)

Fig. 1

Single track model

해당 모델은 타이어 횡력과 횡슬립 관계를 선형으로 가정하였기 때문에 전/후륜 타이어 횡력은 코너링 강성 계수와 타이어 슬립각의 곱으로 표현된다(F_yf = C_fα_f, F_yr = C_rα_r). 식 (1)을 통해 모델의 상태 변수인 차량 횡슬립각(β)과 요레이트(r)는 전/후륜 타이어 조향각(δ_f, δ_r)과 코너링 강성(C_f, C_r)에 의해 결정되는 것을 알 수 있다. 일반적으로 Single track 모델에서 사용되는 전륜 타이어 조향각(δ_f)은 운전자 조향각(Steering wheel angle)에 기어비를 곱하여 사용되고, 후륜 조향각(δ_r)은 0으로 산정하여 사용한다. 하지만, 타이어 조향각의 경우 운전자 조향 입력에 기어비를 곱한 성분과 서스펜션에서 발생하는 롤/컴플라이언스 조향각(Roll/Compliance steer)이 더해져 발생한다. 또한 코너링 강성은 타이어의 특성을 나타내는 변수로 주행 상황에 따라 변화되어야 할 변수임에도 불구하고, 보통의 Single track 모델에서는 상수로 사용되어 모델 오차를 발생시킨다. 따라서 Single track 모델 정확도 개선을 위해서는 언급한 두 오차 요인을 보상해야 한다. 본 논문에서는 서론에 언급한 것과 같이 정밀 센서로 계측된 차량 횡슬립각과 요레이트를 사용하여 코너링 강성 Map을 최적화하는 방법으로 Single track모델의 정확도를 개선하였다. 이때, 전/후륜 조향각의 경우 롤/컴플라이언스 조향각을 고려하지 않고, 전륜은 조향 기어비 Map을 이용하여 도출하고, 후륜 조향각은 0으로 고정하였다. 따라서 정확히 표현하면 본 연구에서는 전/후륜 조향각 오차는 무시하였고, 실제 그 영향은 코너링 강성 Map에 포함되어 보상되는 것이다. 물론 조향각 추정 모델을 적용한 상태로 코너링 강성 Map을 최적화하는 방법도 가능하다.

2.2 코너링 강성 오차 분석

코너링 강성은 타이어 슬립 각 변화에 따른 횡방향 힘의 변화 정도를 나타내는 타이어의 특성 지수이다. 타이어는 비선형적 특성을 가지고 있기 때문에 타이어의 종/수직 방향 힘, 최대 노면 마찰계수, 또는 타이어 슬립각의 크기가 변할 경우 코너링 강성의 크기는 달라진다. 그 중에서도 특히, 차량의 횡 거동으로 인한 횡방향 하중 전이와 타이어 슬립 각에 의한 코너링 강성의 변화가 지배적이다.^7,8)

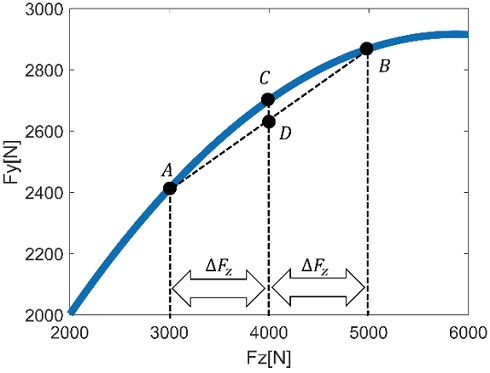
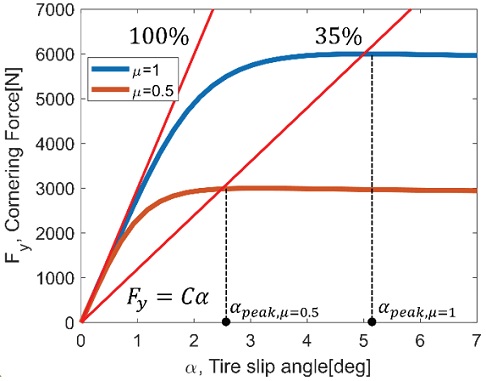
Fig. 2는 동일한 타이어 슬립 각(α = 1deg)에서의 타이어 수직 항력(F_z) 변화에 따른 횡력(F_y) 변화에 대한 곡선이고, Fig. 3은 동일한 타이어 수직 항력 하에서 타이어 슬립각(α)과 횡력 관계를 표현한 것이다.^7,8)

Fig. 2

Relationship of tire vertical force and lateral force at α = 1deg

Fig. 3

Relationship of tire slip angle and lateral force

Fig. 2를 통해 타이어의 수직 항력과 횡력이 비선형적인 관계에 있음을 알 수 있다. 이러한 관계로 인해 실제 차량이 선회할 경우 동일한 타이어 슬립 각이 발생한다해도 좌/우 하중 전이로 인해 횡력이 감소하게 된다. 예를 들면 Fig. 2에서 직진 주행일 경우 선회로 인한 하중 전이가 발생하지 않기 때문에 좌/우 수직 항력은 4000[N]으로 동일하다. 이 상황에서 타이어 슬립 각이 발생한다면 C의 크기만큼 횡력이 발생한다. 하지만 선회 상황에서는 동일한 타이어 슬립 각이라 해도 좌/우 하중 전이로 인해 실제 횡력은 A와 B의 평균 합력인 D 만큼 발생하게 된다. Single track 모델은 좌/우를 하나로 간주하기 때문에 C처럼 평균 합력이 계산되어 모델 오차의 원인이 된다. 따라서 Single track 모델 정확도 개선을 위해서는 횡방향 하중이동에 의해 발생하는 오차를 보상하여야 한다. 이를 위해 횡방향 하중전이에 대한 식을 살펴보면 식 (2)와 같다.^9,10)

$\[ \mathrm{\Delta }{F}_z=k{a}_y \]$

(2)

식 (2)는 차량의 롤 동역학 모델을 통해 도출되었으며, 좌/우 하중 전이에 대하여 횡가속도(a_y)와 게인(k)의 곱으로 표현된다. 즉, 횡가속도가 클수록 횡방향 하중전이량의 크기가 크기 때문에 좌/우 타이어 횡력의 평균 합력이 Single track모델과 같이 좌/우 하나로 간주한 상황보다 감소하게 된다. 따라서 횡가속도가 클수록 평균적인 코너링 강성이 크게 감소하고, 이러한 영향을 적절히 보상하여 코너링 강성을 결정하면 전체적인 모델 오차의 개선이 가능하다.

Fig. 3을 살펴보면 타이어 슬립각과 횡력 또한 비선형적인 관계에 있음을 알 수 있다.^7,8) Single track 모델에 사용되는 코너링 강성은 타이어가 선형적이 특성을 보이는 구간 즉, Fig. 3을 기준으로 타이어 슬립 각이 0에 가까운 영역에서의 기울기를 Nominal 값으로 결정한다. 하지만, Fig. 3처럼 타이어 슬립 각이 증가함에 따라 코너링 강성에 해당하는 기울기가 감소됨을 알 수 있다. 즉, Fig. 3에서 빨간선들은 각각 코너링 강성 Nominal 값의 100 %인 경우, 코너링 강성 Nominal 값의 35 %인 경우에 대해 선형으로 가정된 횡력(F_y=C_α)을 의미하며, 슬립각에 대해 비선형성을 보이는 횡력을 표현하기 위해서는 슬립각이 커질수록 코너링 강성이 Nominal 값보다 작아져야 한다. 따라서 코너링 강성을 Nominal 값에 해당하는 상수로 반영한 Single track 모델은 급격한 주행으로 타이어 슬립 각이 커지는 경우 모델 오차가 발생하게 된다. 그런데 타이어 슬립각은 차량 횡슬립각이 포함되어 차량에서 정확한 측정이 어려운 측면이 있다. 한편 Single track 모델을 유도할 때 횡력의 합력은 전/후륜 코너링 강성과 슬립각의 곱으로 표현(ma_y = C_fα_f + C_rα_r)되므로 일반적인 주행상황에서는 슬립각이 클수록 횡가속도도 또한 크다. 따라서 횡가속도가 큰 경우 횡력-슬립각 곡선의 기울기가 슬립각 0인 지점 보다 감소한다. 이러한 특성을 이용하여 본 연구에서는 횡력-슬립각 곡선에서 보이고 있는 오차 요인을 횡가속도가 증가함에 따라 코너링 강성을 감소시킴으로 모델 오차 개선이 가능 하다고 판단하였다. 더불어 노면 마찰 계수는 횡력-슬립각 곡선의 기울기에 영향을 미치는데, 노면 마찰 계수에 따라 횡력이 포화되는 Peak 슬립각 또한 변화한다. 노면 마찰계수에 따른 Peak 슬립각은 Brush tire 모델에 근거하면 식 (3)과 같이 표현된다.⁸⁾

$\[ \begin{array}{c}{\alpha }_{peak,i}=\frac{3\mu F_{z,i}}{C_{i,nom}}\hfill \\ where i=front, rear\hfill \end{array} \]$

(3)

식 (3)에서 Peak 슬립각은 노면 마찰 계수가 작아짐에 따라 감소하므로 횡력-슬립각 곡선의 기울기 변화는 노면 마찰 계수에 따라 기울기 변화가 이루어지는 슬립각의 범위가 달라지게 된다. 따라서 횡력-슬립각 곡선의 기울기 변화에 의한 오차 요인 개선을 위해서는 노면 마찰 계수도 함께 고려하여 횡가속도에 따라 코너링 강성을 가변 하여야 한다.

본 연구에서는 Fig. 2에서 보인 횡방향 하중 전이에 의한 좌/우 횡력의 합력 감소 특성과 Fig. 3에서 보인 슬립각 증가에 따른 횡력-슬립각 곡선의 기울기 감소 특성으로 인한 모델 오차 요인을 보상하고자 한다. 이를 위해 노면 마찰계수로 정규화한 횡가속도 (a_y/μ)를 입력으로 하는 전/후륜 비선형 Map을 통해 코너링 강성을 가변하여 Single track 모델 정확도를 개선하였다. 제안하는 Single track 모델의 식은 식 (4)와 같다.

$\[ \begin{array}{c}\dot{\beta }=-r+\frac{{\eta }_f{C}_{f,nom}}{m{v}_x}\left({\delta }_f-\beta -\frac{l_f}{v_x}r\right)+\frac{{\eta }_r{C}_{r,nom} }{m{v}_x}\left(-\beta +\frac{l_r}{v_x}r\right)\hfill \\ \dot{r}=\frac{{l_f\eta }_f{C}_{f,nom}}{I_z}\left({\delta }_f-\beta -\frac{l_f}{v_x}r\right)-\frac{{l_r\eta }_r{C}_{r,nom} }{I_z}\left(-\beta +\frac{l_r}{v_x}r\right)\hfill \\ {\eta }_i=ma{p}_i\left(a_y/\mu \right)\hfill \\ where i=Front,Rear\hfill \end{array} \]$

(4)

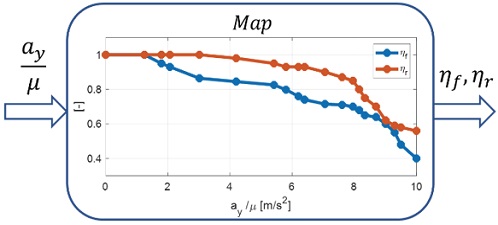
여기에서, C_f,_nom과 C_r,_nom은 전/후륜의 Nominal 코너링 강성으로 선형 영역에서의 코너링 강성 값을 의미하고, η_f와 η_r은 타이어의 비선형성을 보상하기위한 전/후륜 Map을 의미한다. 이때 전/후륜 Map에서 노면 마찰 계수로 정규화된 횡가속도를 입력으로 하는 이유는 Fig. 3에서 보이고 있는 노면 마찰 계수에 따른 횡력-슬립각 곡선의 기울기 변화를 고려하기 위함이다. 전/후륜 Map은 Fig. 4와 같이 보일 수 있으며, 노면 마찰 계수로 정규화된 횡가속도가 커질수록 코너링 강성 보상인자 η_i가 작아지도록 설계되고 0~1사이 값을 가진다. 추가로, 타이어 종방향 힘(F_x)에 따른 슬립율에 의한 영향과 차량 Aerodynamics에 의한 수직항력(F_z) 또한 Fig. 3의 횡력-슬립각 곡선에 영향을 미치지만, 타이어 슬립 각에 대한 영향이 지배적이기 때문에 이 영향들은 무시하였다. 다음 장에서는 식 (4)에서 서술한 Nominal 코너링 강성과 보상 Map을 설계하는 방법에 대해 서술한다.

Fig. 4

Schematics for cornering stiffness error compensation map

3. Data-driven 코너링 강성 오차 개선

앞 장에서는 Single track 모델의 오차 원인을 분석하였고, 그 결과를 기반으로 모델 정확도를 개선하기 위해 Nominal 코너링 강성과 보상 Map 적용이라는 개선 전략을 수립하였다. 본 장에서는 다양한 시나리오의 실차 주행 시험들을 통해 정밀 계측된 차량 횡슬립각과 요레이트의 참값을 Single track 모델의 출력과 비교하여 Nominal 코너링 강성과 타이어의 비선형성을 보상하는 Map을 도출하는 방법에 대해 설명한다.

도출 방법은 다음의 Fig. 5와 같이 주행 시나리오 선정 및 계측, 데이터 전처리, 파라미터 최적화의 흐름으로 진행된다. Fig. 5에서 주행 시나리오 선정 및 계측 정과 데이터 전처리 과정은 파리미터 최적화를 위한 데이터 확보과정이고, 최종적으로 파라미터 최적화 과정을 통해 Nominal 코너링 강성과 기존 Single track 모델에서 고려되지 않은 횡방향 하중 전이와 타이어 슬립각에 의한 코너링 강성의 감소 특성을 고려한 보상 Map을 도출하여 모델 정확도를 개선하였다.

Fig. 5

Schematics for proposed parameter optimization process

3.1 코너링 강성 계수 도출을 위한 데이터 선정

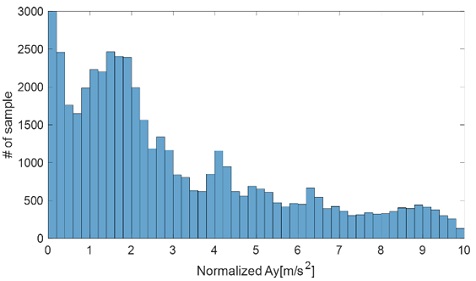
차량에 적합한 코너링 강성의 Nominal 값과 비선형성을 보상하는 Map을 설계하기 위해서는 다양한 횡가속도 영역에 대해 데이터가 분포하는 정상상태(Steady-state) 원선회 주행과 이중 차선 변경(Double Lane Change, DLC)과 같은 과도 주행 상황이 모두 요구가 된다. 특히, 정상상태 원선회 주행 데이터의 중요도가 높은데, 평상적인 선회에 해당되는 낮은 횡가속도 범위에서 부터 마찰한계 근처의 높은 횡가속도 범위까지 정상상태에 있는 차량 횡슬립각과 요레이트 계측치와의 크기를 비교하여 코너링 강성 계수의 Nominal 값과 전반적으로 가속도에 따라 감소하는 Map의 형태를 대부분 도출할 수 있기 때문이다. 이중 차선 변경과 같은 과도 주행 상황 데이터의 경우도 과도 상태에서의 모델 정확도를 제고하기 위해 사용된다. 본 논문에서 국내 자동차社의 후륜 구동 대형 세단을 이용하여 정상상태 원선회, 이중 차선 변경, 유턴과 같이 다양한 상황 아래 주행 데이터를 계측하였다. 시험 차량의 차속, 횡슬립각, 요레이트는 OxTS社의 RT-3100이용하여 계측하였고, 이외의 신호들(차량 IMU, 운전자 조향각, 차량 휠속도 등)은 차량의 CAN 통신을 통해 데이터를 계측하였다. 차속과 노면 마찰계수(μ)는 경우 별도의 추정 방법을 통해 비교적 정확히 알 수 있다고 가정하였다. 본 연구에서 사용된 계측 데이터 중 횡가속도의 데이터 분포는 Fig. 6과 같다. 물론 데이터의 선정은 코너링 강성 최적화 결과에 영향을 끼치고 이는 차량 모델의 정확도를 결정하는바 결국 차량 모델의 용도나 요구되는 특성에 맞게 결정될 수 있다.

Fig. 6

Data sample distribution for parameter optimization

최적화를 위한 주행 데이터는 모두 Dry Asphalt 노면(μ=1)의 주행에서 계측되었다. 계측된 시나리오는 총 46,200개의 Sample로 구성되며 정상상태 원선회(63 %), Slalom 주행(27 %), 유턴 주행(10 %)의 비율로 구성되어 있다. Fig. 6에서 확인할 수 있듯이 횡가속도가 클수록 데이터의 분포는 감소함을 볼 수 있다. 데이터는 일상 주행 영역에 해당하는 0~0.2 G 영역 데이터가 다수 존재하는데, 이는 Nominal 코너링 강성을 도출하기 위해 다 른 횡가속도 영역의 데이터 대비 많이 요구된다. 더불어 횡가속도가 클수록 모델 오차가 증가하므로 높은 횡가속도를 가지는 주행 데이터를 최적화 과정에 포함시키는 것이 모델 정확도 개선을 위해 요구된다. 따라서 본 논문에서는 일반적인 주행상황 뿐만 아니라, 마찰한계 영역까지 주행하는 데이터를 포함하여 Nominal 코너링 강성과 Map을 설계하기 위해 사용하였다.

3.2 파라미터 최적화를 위한 전처리 과정

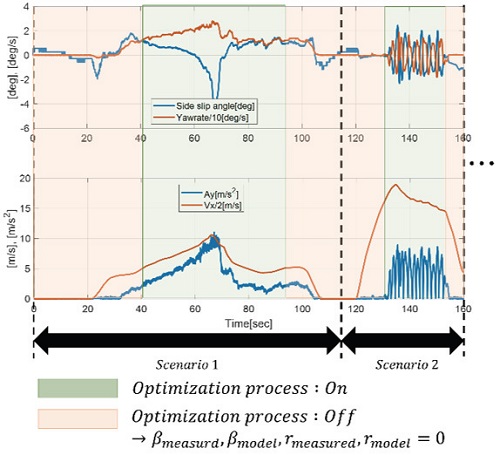
다양한 횡가속도 범위의 주행 데이터가 계측된 후, 코너링 강성 오차 개선을 위한 파라미터 최적화 문제를 해결하기 위해 계측 데이터에 대한 전처리가 요구된다. 우선 계측 데이터를 모두 연결하여 하나의 데이터로 통합한다. Single track 모델은 식 (1)과 같이 횡슬립각(β)과 요레이트(r)에 대한 미분 방정식 이므로 데이터의 전/후 관계가 중요하다. 따라서 정차⟶선회⟶정차의 과정으로 구성된 시험 데이터에서 각 정차 시점을 연결하여 하나의 연속적 데이터로 구성하였다. 이 데이터는 직진주행, 정차상황과 같이 차량의 횡적 거동이 존재하지 않는 상황들도 존재한다. 언급한 두 상황은 코너링 강성의 오차개선을 위한 파라미터 최적화에는 불필요하므로 최적화 연산 시 배제되어야 한다. 따라서 모델 연산은 전 영역에 대해 실시하지만 차속과 횡가속도 계측치가 일정 값 이상, 일정 시간이 유지 시에만 차량의 횡 거동이 있다고 판단하여 해당 상황의 데이터만을 최적화 과정에 고려하였다. 즉, Fig. 7과 같이 차량의 횡 거동이 있는 경우만 최적화 과정에 계측값과 모델 출력간의 에러가 고려되고 그렇지 않는 경우, 계측된 횡슬립각/요레이트와 모델 출력값을 0으로 설정하여 최적화 과정에 고려하지 않도록 모델을 설계 및 데이터 전처리를 실시하였다.

Fig. 7

Data pre-processing for parameter optimization process

3.3 파라미터 최적화 기반 코너링 강성 오차 보상

본 논문에서 제안하는 방법은 Single track 모델 정확도 향상을 위해 다양한 주행시나리오 아래 실차에서 계측한 횡슬립각/요레이트의 참값과 모델 출력값을 비교하며 설계한 전/후륜 타이어 코너링 강성의 Nominal 값과 코너링 강성오차 보상 Map을 통해 모델 정확도 향상을 이끌어 내는 것이다. 이를 위해 식 (5)와 같은 최적화 문제를 구성하여 해당 목적함수를 최소화하는 파라미터들을 도출하였다.

$\[ \begin{array}{c}\underset{X}{\min }{\sum }_{k=1}^N\left(\begin{array}{c}{k}_1{\left({\beta }_{measured}\left(k\right)-{\beta }_{model}\left(k\right)\right)}^2+\hfill \\ k_2{\left(r_{measured}\left(k\right)r_{model}\left(k\right)\right)}^2\hfill \end{array}\right)\hfill \\ s. t\hfill \\ X=\left[C_{f,nom}, C_{r,nom}, {\eta }_{f,5},{\eta }_{f,6}\dots {\eta }_{f,n},{\eta }_{r,5},{\eta }_{r,6}\dots {\eta }_{r,n}\right]\hfill \\ 1.5\times {10}^{5}N/rad\le C_{f,nom},C_{r,nom}\le 3.0\times {10}^{5}N/rad\hfill \\ 0.3\le {\eta }_{f,i}\le {\eta }_{f,i-1}\le 1\hfill \\ 0.3\le {\eta }_{r,j}\le {\eta }_{r,j-1}\le 1\hfill \\ where N :Total \# of sample,i,j :5,... 20\hfill \end{array} \]$

(5)

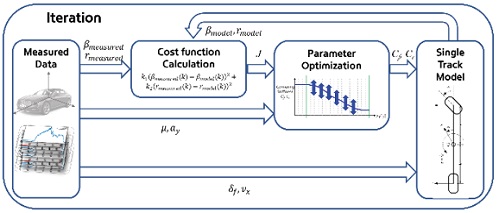
정의한 파라미터 최적화 문제는 모델 출력값(β_model, r_model)과 실제 계측값(β_measured, r_measured)과의 에러로 구성한 목적함수를 최소화하는 것을 목적으로 하며, 3.2절에서 설명한 것과 같이 특정 조건에 대해서만 모델과 계측값과의 에러로 구성된 목적함수를 고려한다. 이때 가중치 k₁, k₂는 횡슬립각과 요레이트의 Scale을 고려하여 결정되고 본 논문에서는 k₁=2, k₂=1로 설정하였다. 식 (5)의 최적화 문제에서 도출하고자 하는 최적 파라미터는 전/후륜 타이어 Nominal 코너링 강성(C_f,_nom, C_r,_nom), 전/후륜 코너링 강성 보상 Map 내부인 자(η_f, η_r)로 구성하였다. 이중 전/후륜 각각의 Map은 횡가속도 0~1.1 G 범위에 균일하게 20개의 인자로 구성하였다. 하지만, Single track 모델의 경우 저횡G 영역에서는 Nominal 코너링 강성만으로도 모델이 비교적 정확하 므로 최적화 파라미터 개수를 감소하기 위해 0.2~1.1 G 영역의 인자들만 최적화 문제에 고려하였다. 즉, η_f,1 ⋯ η_f,4와 η_r,1 ⋯ η_r,4는 모두 1로 고정하였다. 따라서 총 최적화 파라미터 개수는 Nominal 코너링 강성 2개, 전/후륜 개별 0.2~1.1 G 영역에 대항하는 Map인자 32개로 총 34개의 파라미터를 최적화한다. 최적화를 위한 제약조건은 현실적인 코너링 강성의 Nominal 값의 범위와 Map 내부 인자들의 범위를 설정하였다. 특히, Map 내부 인자들은 횡가속도가 커짐에 따라 감소하는 경향을 따르도록 부등식 조건을 최적화 문제에 고려하였다. 정의한 파라미터 최적화 문제를 해결하기 위해 본 논문에서는 MATLAB/Simulink 기반으로 개발 환경을 구축하였고, 해당 프로그램의 Optimization Toolbox에서 제공하는 비선형 프로그래밍 Solver 중 ‘Fmincon’을 사용하여 Offline 상에서 파라미터 최적화를 실시하였다. 최적화 과정에 대한 요약도는 Fig. 8과 같다. Offline 최적화는 i7-8700K, 16 GB RAM 기준 약 10분 정도 소요되었다.

Fig. 8

Parameter optimization process architecture for vehicle single track model

최적화 과정을 통해 도출된 전/후륜 Nominal 코너링 강성과 Map은 서로 곱하여 Fig. 9와 같이 표현하였다(Proposed). 이때 타이어 정보를 기반으로 Zero 슬립 근처에서 계산한 Nominal 코너링 강성(Nominal)과 이를 기반으로 경험적인 방법으로 Map을 직접 수동으로 튜닝 설계한 결과(Manual)도 비교를 위해 표현하였다.

Fig. 9

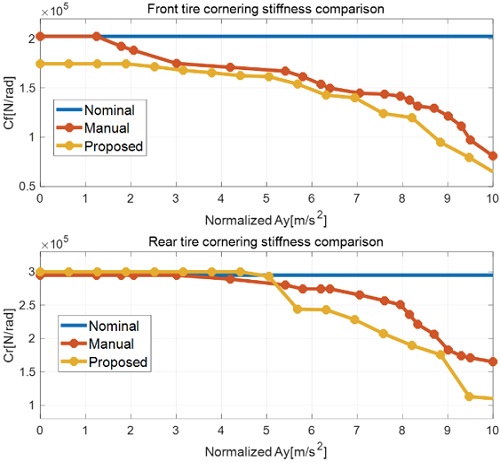
Lateral acceleration-cornering stiffness results by parameter optimization [Up: front tire, Bottom: rear tire]

Fig. 9에서 Nominal 코너링 강성은 고정된 상수이므로 전반적인 횡가속도 영역에 대해 동일한 값을 가진다. Manual로 설계한 결과는 해당분야의 전문가가 여러 실차 데이터에 근거하여 모델 오차가 줄어드는 방향으로 Map의 내부인자들을 수동으로 튜닝 설계하였다. 이러한 이유로 Map 내부 인자들은 정규화된 횡가속도에 균등하게 분할이 되어 있지 않는 특징을 보이고 설계를 위한 시간이 제안 방법 대비 길게 소요된다. 전체적인 형태는 최적화 결과물(Proposed)과 유사하다. 최적화 결과물을 살펴보면, 0~0.2 G 영역에 해당하는 Nominal 코너링 강성은 전륜은 타이어 정보로 산출한 값보다 크게, 후륜은 유사하게 도출되었다. 전륜 코너링 강성은 0.2 G 이상부터 서서히 감소하기 시작하며, 0.7 G 이상의 영역부터 급격하게 감소하는 것을 확인할 수 있다. 후륜 코너링 강성은 0.4 G 이상 영역부터 서서히 감소하며, 0.6 G이상 영역부터 급격한 변화를 보인다. 이러한 원인은 횡가속도가 큰 영역에서는 코너링 강성이 보이는 비선형성이 횡가속도가 작은 영역대비 크기 때문이다. 본 논문에서 사용한 Single track 모델에 사용된 입력은 운전자 조향 입력에 기어비를 곱한 전륜 타이어 조향각만 사용되었기에 차량의 전/후륜 조향각에 존재하는 롤/컴플라이언스 조향각이 배제되어 사용되었다. 조향각 오차도 함께 보상하여 Map을 설계하는 경우 식 (5)의 최적화 과정에서 사용된 모델 대비 전륜 조향 입력은 감소하고, 후륜 조향 입력은 고려되므로 횡가속도 전반적인 영역에 대해 전륜 타이어 코너링 강성은 작게, 후륜 타이어 코너링 강성은 크게 결과가 도출된 것이다. 이러한 코너링 강성의 최적화 결과는 최적화에 사용된 데이터 셋의 종류, 차량 종류(세단, SUV 등), 타이어 종류, 차량의 구동 형태(전륜 구동, 후륜구동 등)에 따라 달라지게 된다.

4. 실차 검증

파라미터 최적화 과정을 통해 도출된 코너링 강성을 Single track 모델에 적용하여 실차 데이터에 대한 모델 검증을 수행하였다. 기본 방법들 대비 모델 정확도 개 선을 확인하기 위해 전/후륜 타이어 코너링 강성을 Nominal 값으로만 사용한 모델(Conventional)과 엔지니어가 데이터에 기반하여 경험적인 방법으로 수동 튜닝 설계한 코너링 강성 Map을 적용한 모델(Manual), 그리고 본 논문에서 제안하고 있는 최적화 방법을 통해 도출된 결과를 적용한 차량 모델(Proposed)의 횡슬립각과 요레이트를 정밀 센서의 계측값과 비교하였다. 이때 각 모델의 출력값과 계측값의 에러를 별도로 표현하였다. Table 1은 모델 정확도 개선을 검증하기 위해 정의된 실차 주행 시나리오 목록이다. Case 1은 반시계 방향으로 서서히 가속 주행하며 마찰 한계 영역까지 가혹하게 주행하는 상황, Case 2는 고속 Slalom 주행 상황, Case 3은 유턴 상황 주행 상황이다. 3가지 주행 상황 모두 Dry asphalt 노면(μ=1)에서 실시되었다.

Table 1

Driving scenarios for experimental tests

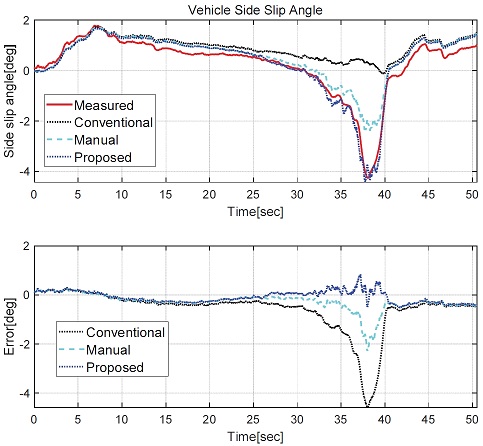
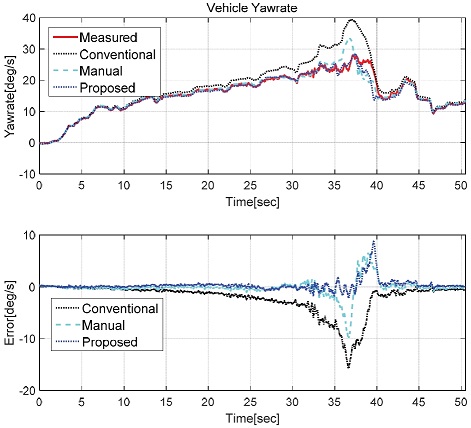
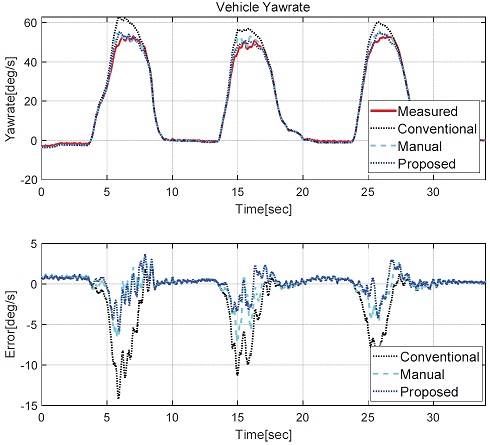
Figs. 10~11은 Case 1인 원선회 주행상황에 대한 차량 횡슬립각과 요레이트의 비교 결과이다. 정상상태에 준하게 서서히 가속 주행하며 원선회가 이뤄지고 37초 부근에서 계측 횡가속도 기준으로 최대 횡가속도 0.98 G를 보인다. Fig. 10에서 횡슬립각에 대한 결과를 살펴보면, 기존 모델(Conventional)의 경우 마찰 한계에 근접해지는 30~40초 구간에서 절댓값 기준 최대 4.2 deg정도로 오차가 크게 발생하였다. Manual은 기존 모델 대비 25~30초 구간에 대해서는 참값과 유사한 결과를 보이지만, 37초 구간과 같이 노면 한계 가속도(μg)인 1 G에 준하는 구간의 경우 2 deg내외의 오차를 보이고 있다. 본 논문에서 제안하고 있는 파라미터 최적화 결과를 적용한 모델은(Proposed)은 전체적인 구간에 대해 최대 1도 미만의 오차를 보이는 것을 확인할 수 있다. 이는, 수동으로 코너링 강성의 오차를 보상하는 방법 대비 제안하고 있는 방법이 좀더 높은 정확도 개선을 보이고 있음을 보인다. Fig. 11은 요레이트에 대한 결과 비교이다. Fig. 10에서 보이고 있는 횡슬립각 비교 결과와 유사하게 기존 모델은 횡가속도가 증가하고 있는 25~40초 구간에 대해 절댓값 기준 최대 15 deg/s 정도 오차가 발생한다. Manual과 제안 모델은 기존 모델 대비하여 에러가 감소되어 정확도가 개선되었다. 제안 모델은 Manual과 비교할 때 유사한 결과를 보이고, 마찰 한계에 근접하는 35~37초 구간에서 제안모델이 성능적으로 우세를 보임을 확인할 수 있다. 제안 모델은 전체적으로 절댓값 기준 2 deg/s 미만의 요레이트 에러를 가지며, 최대 요레이트 에러는 8 deg/s 정도로, 기존 모델이 보이고 있는 10 deg/s 대비하여 감소하였기에 전반적인 성능 개선을 확인하였다.

Fig. 10

Vehicle sideslip angle accuracy validation for case 1

Fig. 11

Vehicle yawrate accuracy validation for case 1

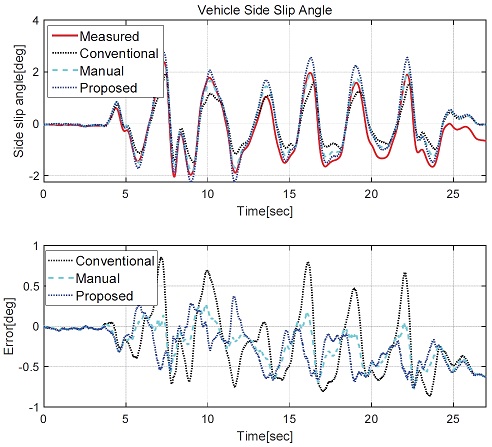
Figs. 12~13은 Case 2에 속하는 고속 주행에서의 Slalom 주행을 통해 횡슬립각과 요레이트를 비교하였다. Fig. 12에서 횡슬립각에 대한 결과를 비교하면, 기존 모델은 Peak 지점들에 대해서 절댓값 기준 항상 작게 결과를 도출하는 것을 확인할 수 있다. Manual과 제안 모델은 유사한 정확도를 보이며 기존 모델 대비 오차를 개선하였음을 보인다. 기존 모델은 최대 0.8 deg의 에러를 보이고 있지만, Manual과 제안 모델은 최대 0.7 deg 미만을 보이며 정확도가 소폭 상승하였다. Fig. 13은 요레이트에 대한 비교 결과이다. 기존 모델의 경우 최대 7 deg/s의 오차를 보이며 Slalom 주행 시 Peak영역에서 절댓값 기준 계측값 대비 항상 큰 값을 보인다. Manual과 제안 모델은 Peak 영역에 대해 기존 모델 대비 오차가 크게 감소하여 정확도 향상이 되었음을 확인하였다. 두 모델 모두 유사한 결과를 도출하지만, 전반적인 영역에 대해 Manual 대비 제안 모델이 오차가 작음을 보이고 있다. 추가적으로, Case 2에서 제안모델의 정확도 향상율은 Case 1 대비하여 낮음을 보이는데, Case 2와 같은 고속 주행상황에서는 Case 1 대비 제안 방법에서 고려하지 않은 차량 Aerodynamics에 의한 수직항력(F_z)의 영향이 크기 때문이다. 따라서 타이어 수직방향힘을 추가로 고려하여 코너링 강성 오차를 보상하는 경우 정확도 향상율을 높일 수 있다.

Fig. 12

Vehicle sideslip angle accuracy validation for case 2

Fig. 13

Vehicle yawrate accuracy validation for case 2

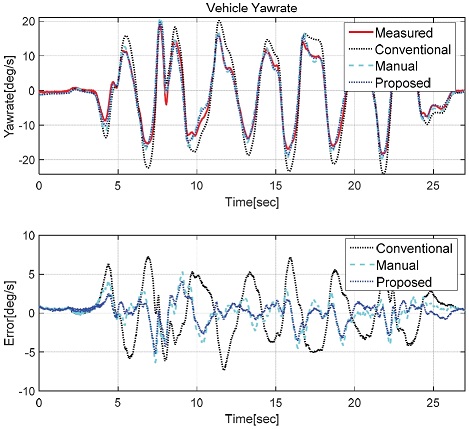
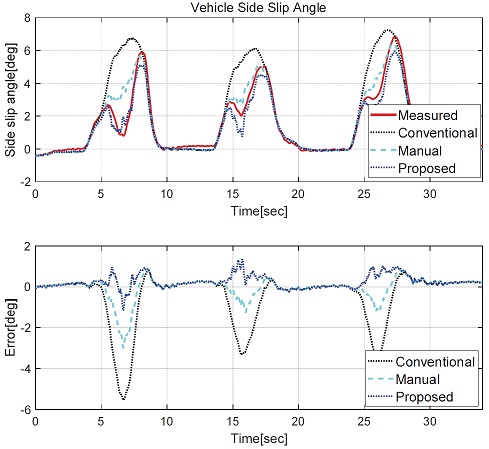
Figs. 14~15는 Case 3의 유턴 상황에 대한 횡슬립각/요레 이트 비교 결과이다. Case 3은 Case 2와 유사하게 급격한 조향으로 인한 과도 상황에서의 검증을 위해 진행되었다. Fig. 14에서 보이고 있는 횡슬립각에 대한 결과를 비교하면, 기준 모델은 과도 주행 상황이 발생하는 6, 16, 26초 구간에 대해 큰 오차를 보이고 있다. 기준 모델은 코너링 강성 오차를 보상하지 않아 정확도가 떨어짐을 보인다. 한편, Manual은 기존 모델 대비하여 정확도는 상승하였으나, 코너링 강성 보상 Map 내부 인자들 간의 변 화가 잘 고려되지 않아 6, 16, 26초 구간에서 오차를 보이고 있다. 하지만, 논문에서 제안하는 방법을 적용한 모델은 파라미터 최적화를 실시할 때 Case 2~3과 같은 과도 조향 상황도 고려되어 제안 모델이 오차가 작음을 확인할 수 있다. Fig. 15는 요레이트에 대한 비교 결과이다. Fig. 14에서 보인 횡슬립각과 달리 요레이트는 과도 조향에도 차량의 조향각 입력과 비슷한 양상을 보인다. 따라서 기준 모델의 요레이트 형태는 큰 오차를 보이지 않으나, Peak 지점에 속하는 7, 17, 27초 구간에 대해서는 최대 15 deg/s 정도의 큰 오차를 보이고 있다. 한편, Manual과 제안 모델은 큰 정확도 향상을 도출하였다. 두 모델은 유사한 결과를 보이지만, 제안 모델이 Manual 대비 오차가 작음을 확인할 수 있다. 특히, 15초 구간에서 Manual은 최대 7 deg/s의 오차를 보이지만, 제안 모델은 3 deg/s의 오차를 보인다. 이러한 횡슬립각과 요레이트에 대한 비교 결과를 볼 때, 본 논문에서 제안하는 실험 계측 데이터를 활용한 파라미터 최적화 기반의 방법이 Single track 모델의 정확도를 대폭 향상시키며 Manual보다 설계 시간이 단축되었고 정량적인 정확도 개선을 가지고 옴을 확인하였다. 제안 방법은 최적화에 사용되는 데이터나 목적함수의 가중치에 따라 결과는 달라 질 수 있으며 이는 용도에 맞게 개발자가 정의 가능하다.

Fig. 14

Vehicle sideslip angle accuracy validation for case 3

Fig. 15

Vehicle yawrate accuracy validation for case 3

제안한 Single track 모델 정확도 개선 방안은 계측데이터를 활용하여 차량의 횡 거동에 의한 코너링 강성계수 오차만을 고려한 방법이지만, 전/후 조향각 오차와 종방향 힘 또는 수직 방향 힘에 대한 영향을 고려할 경우 더욱 오차 개선이 가능하다.

5. 결 론

본 논문에서는 다양한 제어 및 추정 로직에서 활용되는 차량 횡방향 Single track 모델의 정확도 향상을 위해 다양한 실차 시험 시나리오 상황에서 계측된 데이터를 기반의 코너링 강성 오차 보상 방법을 제안하였다. 제안 오차 보상 방안은 다양한 시험을 통해 계측한 차량의 실제 횡슬립각/요레이트와 모델 출력값과의 에러를 최소화하도록 파라미터 최적화 문제로 구성하여 코너링 강성 계수의 오차를 보상하였다. 제안 연구는 실차 시험 데이터를 통해 설계 및 검증되었으며 다양한 시나리오 아래 기존 방법에 의해 도출된 모델 대비 차량의 횡슬립각과 요레이트의 정확도가 대폭 개선됨을 확인할 수 있었다. 특히, 파라미터 최적화 기반의 오차 보상 방법은 해당 분야의 엔지니어가 경험적인 방법으로 수동 튜닝 설계한 오차 보상 방안 보다 간편하고, 튜닝 시간을 단축하면서도 개선된 정확도를 보인다. 하지만 해당 방식은 저마찰 노면 상황에 대해 추가 검증이 요구되고, 조향각 오차와 타이어 종/수직방향힘이 Single track 모델에 끼치는 영향을 추가 고려하여 그 성능을 향상시킬 수 있다. 따라서 향후 연구에서는 해당 사항들을 고려하여 제안 방법을 발전시킬 예정이다. 결국 해당 방법을 통해 정확도가 개선된 Single track 모델은 전반적인 차량 횡방향 제어에 있어 개선된 모델을 사용하게 됨으로써 차량 제어 성능 개선에 기여할 수 있기를 기대한다.

Acknowledgments

이 성과는 2020년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(2017R1A1A1A05069503). 이 논문은 2020학년도 한국기술교육대학교 교육연구진흥과제 지원에 의하여 연구되었음. 이 논문은 교육부와 한국연구재단의 재원으로 지원을 받아 수행된 사회맞춤형 산학협력 선도대학(LINC+) 육성사업의 연구 결과임. 이 연구는 2021년도 산업통상자원부 및 산업기술평가관리원(KEIT) 연구비 지원에 의한 연구임(20015831). 본 연구는 2021년도 교육부의 재원으로 한국연구재단의 지원을 받아 수행된 지자체-대학 협력기반 지역혁신 사업의 결과임(2021RIS-004).

References

• P. Falcone, F. Borrelli, J. Asgari, H. E. Tseng and D. Hrovat, “Predictive Active Steering Control for Autonomous Vehicle Systems,” IEEE Transactions on Control Systems Technology, Vol.15, No.3, pp.566-580, 2007. [https://doi.org/10.1109/TCST.2007.894653]
• M. Choi and S. B. Choi, “Model Predictive Control for Vehicle Yaw Stability with Practical Concerns,” IEEE Transactions on Vehicular Technology, Vol.63, No.8, pp.3539-3548, 2014. [https://doi.org/10.1109/TVT.2014.2306733]
• K. Han and G. Park, “Lateral Motion Control of Electronic-Four-Wheel Drive Vehicles for Enhancement of Cornering Performance,” Transactions of KSAE, Vol.28, No.9, pp.605-611, 2020. [https://doi.org/10.7467/KSAE.2020.28.9.605]
• A. Rucco, G. Notarstefano and J. Hauser, “Dynamics Exploration of a Single-track Rigid Car Model with Load Transfer,” IEEE Conference on Decision and Control, pp.4934-4939, 2010. [https://doi.org/10.1109/CDC.2010.5718133]
• K. Cho, H. Na, W. Cho and S. H. You, “Estimation of Vehicle Steering Angle for Improving Accuracy of Vehicle Lateral Single Track Model,” Transactions of KSAE, Vol.29, No.7, pp.603-608, 2021. [https://doi.org/10.7467/KSAE.2021.29.7.603]
• K. Cho, H. Na and S. H. You, “Accuracy Improvement of Vehicle Lateral Single-Track Model,” Proceedings of the 14th International Symposium on Advanced Vehicle Control, 2018.
• T. D. Gillespie, Fundamentals of Vehicle Dynamics, SAE International, 1992. [https://doi.org/10.4271/R-114]
• H. Pacejka, Tire and Vehicle Dynamics, Elsevier, 2015.
• C. H. Yoon, H. J. Jin and S. H. You, “Real-Time Self-Aligning Torque Estimation,” Transactions of the Korean Society of Mechanical Engineers – A, Vol.42, No.4, pp.363-369, 2018. [https://doi.org/10.3795/KSME-A.2018.42.4.363]
• S. H. You, J. O. Hahn and H. Lee, “New Adaptive Approaches to Real-time Estimation of Vehicle Sideslip Angle,” Control Engineering Practice, Vol.17, No.12, pp.1367-1379, 2009. [https://doi.org/10.1016/j.conengprac.2009.07.002]