병렬 배터리 팩의 온도 불균형 검출 방법론 연구

1. 서 론

오늘날 신재생 에너지는 탈 석유화, 환경오염 등의 이슈로 선택이 아닌 필수가 되었다. 다양한 방식의 재생 에너지 생산과 더불어, 에너지를 저장하는 장치 또한 필수적인 요소이다. 재생 에너지의 특성상 불규칙한 전기를 생산하게 되는데, 이런 불규칙한 전기를 저장 장치에 저장 한 후, 의도하는 출력으로 사용할 수 있기 때문에 에너지 저장 장치의 사용은 필수적이다. 다양한 방식의 에너지 저장 장치 중에서도 최근 리튬 이온 이차 전지에 대한 관심이 증가하고 있다. 리튬 이온 이차 전지는 Hybrid electric vehicle(HEV), Plug-in Hybrid electric vehicle(PHEV), Battery electric vehicle(BEV), Energy Storage System(ESS) 등 다양한 어플리케이션에 적용되며, 높은 에너지밀도, 장수명 특성으로 에너지 저장이 필요한 곳의 핵심 요소로 자리 잡고 있다. 이렇게 배터리에 대한 관심이 증가하면서 배터리 관리 시스템(Battery Management System; BMS)에 대한 중요성도 부각되고 있다. BMS는 배터리로부터 얻은 전압, 전류, 온도 정보들을 토대로 배터리의 상태, 성능 및 안전성을 진단하고 추정한다. 특히, 전압 정보는 배터리의 상태, 노화, 이상 거동 등을 진단할 수 있는 주요한 정보이다. 그러나 배터리의 구성에 따라 전압 정보의 제약을 받는 상황이 발생한다. 배터리는 보통 개별 배터리 셀이 아닌 배터리 팩 단위로 구성한다. 개별 배터리 셀의 용량 및 출력의 한계로 인해 직병렬 조합을 통한 배터리 팩 구성이 필수적이다. 직렬 조합의 경우, 각 개별 배터리 셀의 전압 정보를 알 수 있어 배터리 상태 진단이 용이하다. 그러나 병렬 조합의 경우, 병렬 구성 내의 모든 배터리 셀의 전압이 하나의 전압으로 합성되어 개별 배터리 셀들의 상태 변화를 감지하기 어려운 단점이 있다. 따라서 병렬 배터리 팩 내의 개별 배터리 셀의 변화를 병렬 배터리 팩 단위의 정보를 통해 검출 하는 방안이 필요하다.

배터리는 충⋅방전 하는 과정에서 열이 발생하게 되는데, 이 열을 제어해 주는 것 또한 배터리의 성능과 안전성에서 중요한 요소이다. 배터리의 충⋅방전 과정 중에 발생하는 열 뿐만 아니라 제조상의 결함, 오사용, 사용 환경 등에 의해 비정상적인 열이 발생하는 경우가 있다. 이 경우, 배터리의 열적 상태(State-Of-Temperature; SOT)를 빠르게 진단해 적절한 조치를 해주는 것이 중요하다. 배터리의 SOT를 진단하는 방법에는 직접적인 측정 방법과 전기적 신호를 통해 간접적으로 진단하는 방법이 있다. 직접적인 측정 방법은 배터리에 온도 센서를 부착하여 온도를 측정하는 방법이며 가장 일반적으로 사용하는 방식이다. 이 방법은 배터리의 SOT를 가장 직관적으로 나타내는 방식이다. 하지만 수많은 배터리 셀의 직렬과 병렬 구성을 통해 이루어지는 에너지 저장 장치의 특성상 모든 배터리 셀에 온도 센서를 부착하는 것이 제한된다. 상업적으로 양산되는 배터리 팩의 경우, 원가, 공정 등의 측면에서 수십 개의 온도 센서를 적용하는 것은 불가능하기 때문이다. 전기적 신호를 통해 간접적으로 진단하는 방법으로는 배터리 팩에 인가된 전류 및 전압 특성을 통해 추출된 파라미터를 통해 열적 특성을 추정하거나, 전기적 파라미터를 사용한 열 모델링을 통해 SOT를 추정 하는 방식이다. 이 방법은 배터리의 전기적 특성을 이용한 것으로 직접적인 측정 방법보다 제약이 적으며, 관련 연구도 활발히 진행 중이다.^1,2) 그러나 SOT 추정을 위해 사용하는 전기적 모델은 배터리 내부의 물리적 작용의 정교한 반영이 제한되며, 전기 화학적 모델은 내부에 비선형 편미분 방정식을 포함하고 있어 계산이 복잡하다는 단점이 있다.³⁾ 특히, 배터리 병렬 팩으로 구성된 경우, 위의 설명과 같이 검출에 제약이 있다.

본 논문에서는 배터리의 전기적 특성을 통해 병렬 배터리 팩 내의 배터리 셀 간 온도 불균형 상태를 검출할 수 있는 방법을 연구한다. 기존의 배터리 병렬 팩에 대한 연구는 온도 불균형에 의한 전류 불균형, 충전 상태(State-Of-Charge; SOC) 불균형을 다루거나,^4,5) 이렇게 발생한 전류 및 SOC 불균형이 배터리 성능에 미치는 영향^6,7) 등 병렬 배터리 팩의 온도 불균형에 대한 현상 및 영향을 연구한다. 본 연구는 이런 불균형에 대해 직접적 측정 방식이 아닌 전기적 특성을 사용한 검출 방식을 연구한다. 병렬 팩의 온도 불균형은 장기적 성능 저하의 원인이 되며, 안전성 문제,⁸⁾ 온도 불균형에 따른 SOC편차 발생⁹⁾에 의한 효율 저하, 배터리 성능 저하¹⁰⁾ 등 배터리에 부정적인 영향을 미친다. 따라서 병렬 배터리 팩의 온도 불균형 상태를 검출할 수 있는 배터리 전기적 특성과 그 추출 방법 연구가 필요하다. 전기적 특성은 SOC 및 온도 불균형 환경에 대한 배터리 파라미터들의 변화를 통해 확인하여 어떤 파라미터가 온도 불균형을 대변하는지 연구하였다. 특히 병렬 배터리 팩의 파라미터 특성을 파악하기 위해 온도 조건에 따른 배터리 셀 단위 실험을 선행하였다. 또한 추출 방식에 따른 파라미터 차이를 검증하기 위해 두 가지 방법을 비교하였다. 개방회로전압(Open-Circuit-Voltage; OCV) 회복 구간을 통한 파라미터 추출 방식과, Hybird Pulse Power Characterization(HPPC) 방식을 통한 파라미터 추출 방식이다. 본 논문에서는 두 가지 방식 중 어떤 방식이 병렬 배터리 팩의 온도 불균형 검출에 적합한지 연구한다.

2. 리튬이온 배터리 등가 회로 모델

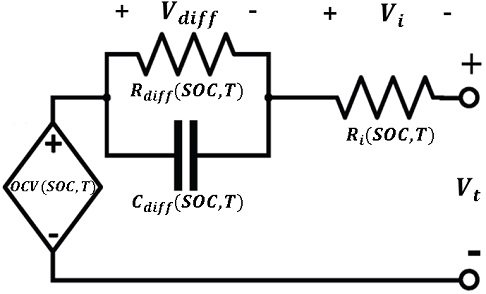
배터리 등가 회로 모델은 Fig. 1과 같이 나타낼 수 있다. 배터리 등가 회로의 파라미터는 배터리의 전압, 전류 특성을 기반으로 산출한다. 등가 회로는 OCV, 오믹 저항(R_i), 분극 저항(R_diff), 분극 캐패시터(C_diff)로 구성되어 있다. 각각의 파라미터들은 SOC와 온도에 영향을 받는다. 일반적으로 저항은 SOC와 온도가 낮을수록 큰 값을 보이며, 캐패시터는 온도가 낮을수록 작은 값을 보인다. 개방회로전압은 배터리 내부 양 전극의 전위차를 전압원으로 나타낸 것이다. 배터리의 충⋅방전 중의 전압은 OCV와 다른 값을 나타내는데, 이는 오믹 저항과 분극 저항에 의해 배터리의 단자 전압이 영향을 받기 때문이다. 배터리가 충⋅방전을 중단하게 되면, 저항에 의해 발생된 분극 전압이 감소되며 종단 저항은 OCV로 수렴하게 된다. 이 과정이 분극 캐패시터로 표현된다.

Fig. 1

Equivalent circuit model of battery

배터리 등가 회로에 의하면 배터리 전압의 거동은 식 (1)과 같이 표현 할 수 있다. 그러나, 배터리 전압의 동적 특성은 SOC 마다 다르며, 식 (1)의 지수 함수로 OCV에 수렴하는 이론적인 전압 거동과는 일치하지 않는 경향을 보이기도 한다. 왜냐하면, 배터리는 전기 화학적 작용을 통해 작동하는 장치이며, 4가지 구성요소(양극재, 음극재, 전해액, 분리막)의 계면 반응, 내부 반응들의 영향을 받기 때문이다. 하지만, 등가 회로의 파라미터가 온도에 의해 변화하기 때문에 이것을 통해 온도 불균형을 진단하는 것은 유의미하다. 따라서 본 논문에서는 등가회로에 의한 파라미터를 통해 온도 불균형을 진단한다.

2.1 OCV 회복 구간을 통한 등가 회로 모델 파라미터 추출

OCV 회복 구간을 통한 파라미터 추출 방식은 배터리에 인가된 전류가 차단된 시점부터 전압이 정상상태에 도달하는 시점까지의 구간을 통해 파라미터를 산출한다. 이론적으로 배터리 등가 회로에 해당하는 파라미터를 추출하기 위해서는 전압이 정상 상태에 도달해야한다. 이 점에서 이 방식은 이론적으로 적합한 방식이지만, 파라미터 산출에 비교적 긴 시간이 필요하다는 단점이 있다.

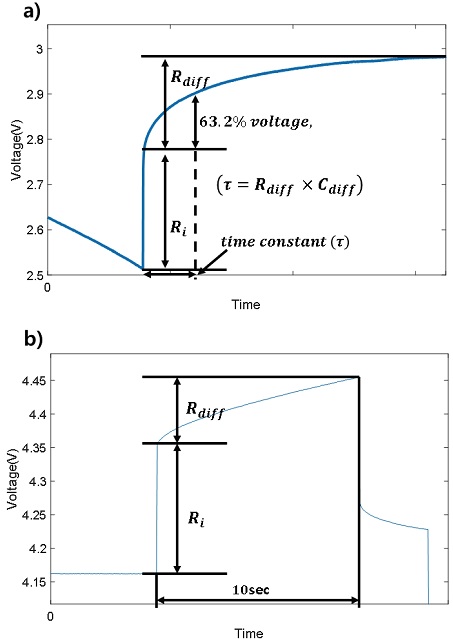
각 파라미터들은 Fig. 2의 a)와 같이 추출한다. R_i의 경우, 배터리에 인가된 전류를 전류 차단 직후 순간적으로 변화되는 전압의 변화에 나누어 산출한다. R_diff의 경우, R_i를 추출한 직후의 전압부터 최종적으로 수렴한 전압(OCV)의 차이에 인가되었던 전류를 나누어 산출한다. 그리고 그 구간에서 전체 전압 변화의 63.2 %의 전압이 변화된 시점이 Time constant이며, Fig. 2의 a의 식을 통해 C_diff를 산출한다.

Fig. 2

Methodology of extracting battery parameters a) using OCV recovery section b) using HPPC method

3. 배터리 셀 단위 파라미터 추출

본 장에서는 2장에서 설명한 2가지 방식으로 배터리 셀 단위의 파라미터를 추출한다. 사용된 배터리 셀은 SAMSUNG INR-21700-50E이다. 온도에 따른 파라미터를 비교하기 위하여 상온(25 ^oC) 및 고온(40 ^oC)에 노출 된 배터리 셀을 각 시험을 통해 파라미터를 산출하였다.

3.1 OCV 회복 구간을 통한 파라미터 추출

Fig. 3은 OCV 회복 구간을 통하여 추출한 파라미터이다. 오믹 저항의 경우, 고온에 노출된 배터리 셀이 전 구간에서 작은 값을 보인다. 분극 저항의 경우도 마찬가지로 고온에 노출된 배터리 셀이 전 구간에서 작은 값을 나타내고 있다. 상온 노출 배터리 셀과 고온 노출 배터리 셀의 전 영역에서의 저항 값의 평균은 오믹 저항이 각각 26.6 mΩ, 24.8 mΩ이며, 분극 저항이 각각 24.5 mΩ, 17.6 mΩ 이다. 2가지 배터리 셀 사이의 편차는 상온 배터리 셀이 고온 배터리 셀 대비 오믹 저항이 7.2 %, 분극 저항이 39 % 크게 나타난다. 분극 캐패시터의 경우, SOC 65~75 % 구간에서 다른 SOC 구간과는 다른 경향을 보인다. 해당 구간에서 고온 노출 배터리 셀의 캐패시터 값이 상온 노출 배터리 셀보다 약 46 % 높은 값을 보인다. 캐패시터 값은 Fig. 2에 표현된 것처럼 분극 저항과 시정수의 영향을 받는데, 분극 저항이 전 영역에서 일정한 편차를 갖기 때문에 시정수의 영향으로 캐패시터 값의 변화가 발생하는 것으로 볼 수 있다. 시정수는 전압이 회복되는 속도와 관련이 있다. 일반적으로 온도가 높을수록 회복 속도가 빨라지는 경향을 보이기 때문에¹⁴⁾ 낮은 값을 가질 것으로 예상되었으나, SOC 65~75 %에서는 고온에 노출된 배터리 셀의 시정수가 상대적으로 큰 값으로 추출되었다.

Fig. 3

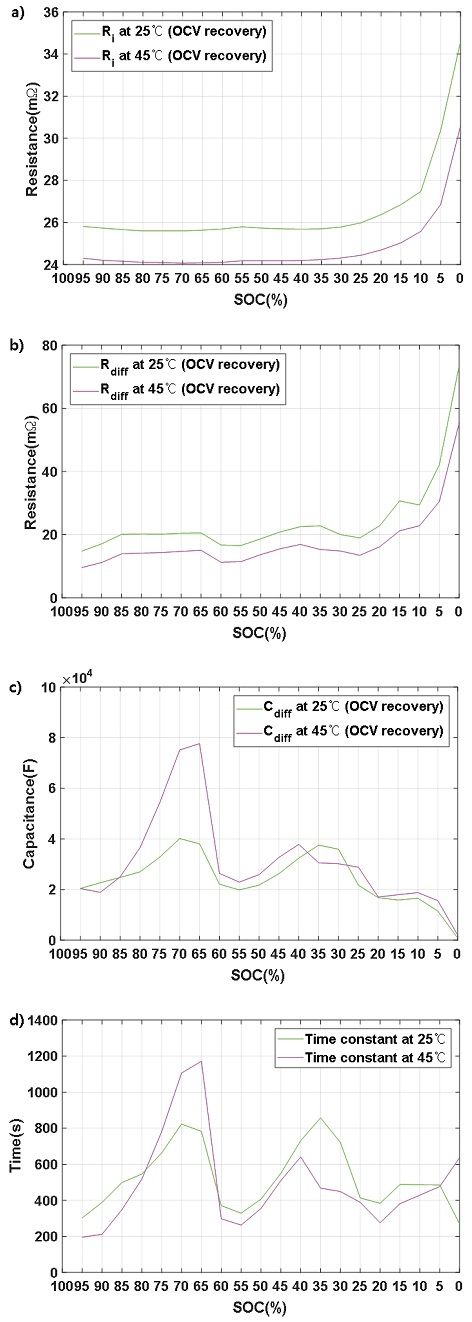
Battery cell level parameters at 25 oC ambient cycle and 45 oC ambient cycle using OCV recovery section a) Ohmic resistance b) Diffusion resistance c) Diffusion capacitance d) Time constant

배터리 셀의 특정 SOC, 특정 온도에 따라 동적 특성이 달라지는 것은 전기 화학적으로 설명된다. 배터리가 충방전을 하면, 전극과 전해액 사이에 서로 다른 전하가 대전 되며 전기이중층(Electrical double layer; EDL)이 형성된다. 이 EDL이 등가 회로 모델에서 캐패시터로 대변된다. 이 EDL은 서로 다른 전하에 의해 발생하는 정전기력 및 화학적 흡착력이 전해질 농도에 의한 확산력과 평형을 이루며 구성 된다.¹⁵⁾ 결국 위의 세 가지 요인들에 의해 OCV회복 중 전압의 동적 특성이 결정된다. 이런 전기화학적 특성으로 인해 전기적 등가 회로 모델의 캐패시터와 전기화학적 작용에 의한 전기이중층은 다른 거동을 보이게 된다. 위의 각 요인들이 SOC와 온도에 따라 변화하며 전압 회복 경향에 영향을 미치며, 결국 캐패시터 값에 영향을 미치는 것으로 판단된다.

3.2 HPPC 방식을 통한 파라미터 추출

Fig. 4는 HPPC 시험을 통해 추출한 파라미터이다. 오믹 저항의 경우, 고온에 노출된 배터리 셀이 전 구간에서 작은 값을 보인다. 분극 저항의 경우도 마찬가지로 고온에 노출된 배터리 셀이 전 구간에서 작은 값을 보인다. 분극 캐패시터의 경우, 고온에 노출된 배터리 셀이 전 구간에서 큰 값을 보인다. OCV 회복 구간을 통해 산출한 값과 달리 특이점이 없다.

Fig. 4

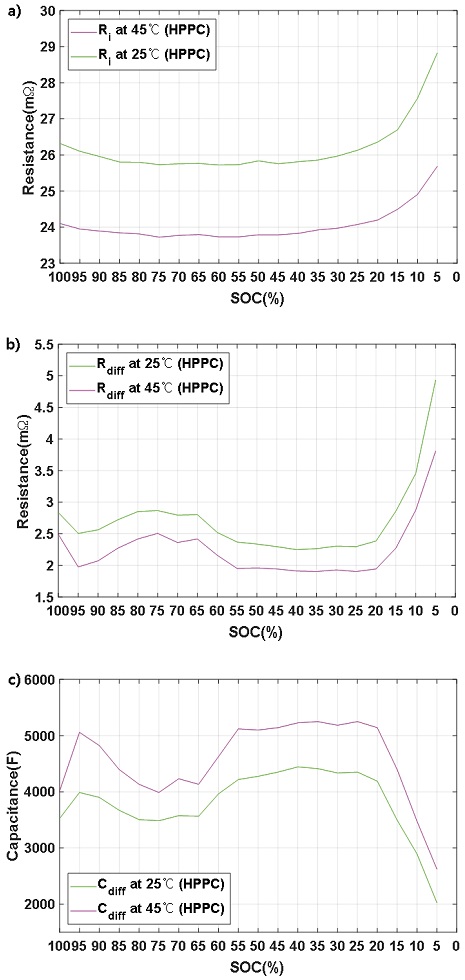
Battery cell level parameters at 25 oC ambient cycle and 45 oC ambient cycle using HPPC method a) Ohmic resistance b) Diffusion resistance c) Diffusion capacitance

HPPC 시험 방식의 경우, 보통 10초, 20초, 30초 등 단시간 동안의 전류 인가를 통하여 추출된 전압을 통해 파라미터들을 산출한다. 그렇기 때문에 배터리의 동적 특성이 잘 드러나지 않는다. Fig. 3에서 OCV 회복 구간을 사용할 경우, 시정수의 값이 평균 519초로 HPPC 시험의 전류 인가 시간인 수십 초는 동적 특성 반영에는 충분하지 않음을 알 수 있다.

4. 온도 불균형 배터리 팩 파라미터 실험

3장을 통해 파라미터 추출 방식에 따라 추출되는 값들이 달라지며, OCV 회복 곡선을 통한 추출에서는 특정 SOC, 온도 조건에서 특이점을 갖는 것을 확인하였다. 이런 배터리 셀의 특징을 이용하여, 온도 불균형 병렬 배터리 팩에서의 파라미터 특이점을 실험을 통해 분석 및 검증하였다.

4.1 온도 불균형 배터리 팩 실험 세팅

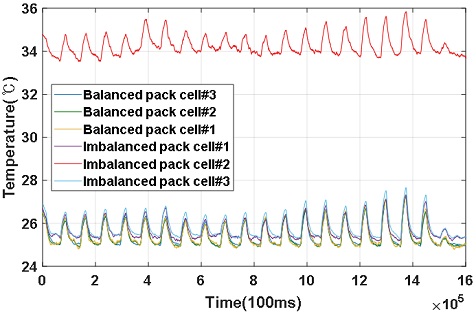
기존 연구에서 병렬 배터리 팩의 온도 불균형을 모사하는 방법은 일반적인 사용 범위의 온도 불균형 혹은, 단열재로 발열이 아닌 방열을 통제하여 온도 불균형을 모사하였다.^4,5) 그러나 이런 방법은 셀의 비정상적인 발열을 모사 할 수 없다. 따라서 본 연구에서는 배터리 셀에 직접적인 발열을 가하였다. 본 실험은 Fig. 5와 같이 2가지 3P1S 병렬 배터리 팩을 구성하였다. 온도 균형 배터리 팩은 3개의 셀 모두 상온 조건에 노출된 병렬 배터리 팩이며, 온도 불균형 배터리 팩은 3개의 셀 중 하나의 배터리 셀에 고온 조건, 나머지 2개의 배터리 셀들은 상온 조건으로 구성한다. 배터리 셀에 고온 조건을 모사하기 위해 히터와 단열재를 적용하여 약 1W를 인가하였으며, Fig. 6과 같은 온도 거동을 구현하였다. 적용된 1W는 초기 내부 단락(Internal Short Circuit; ISC)이 발생 했을 경우의 저항을 고려한 값이다.¹⁶⁾ 이 열량은 ISC 뿐 아니라, 배터리 팩에서 발생할 수 있는 외부적 요인(용접 불량, 도선 체결 불량, 기구적 간섭 등)에 의해 발생 가능한 열량을 대변한다.

Fig. 5

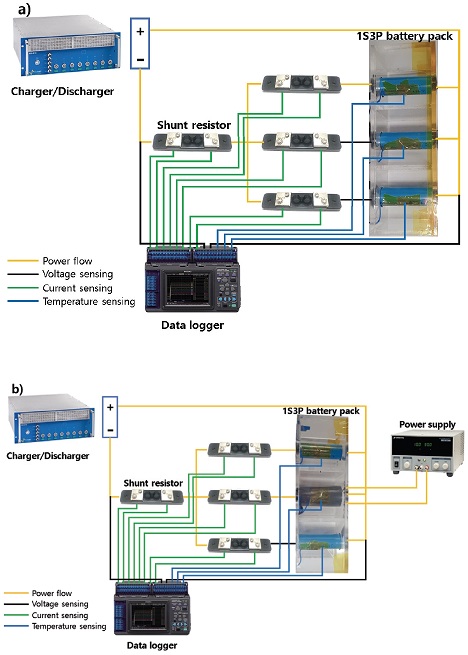
Diagram of the experiment for parallel battery packs a) thermal balanced 1S3P battery pack b) thermal imbalanced 1S3P battery pack

Fig. 6

Temperature of cells in balanced and imbalanced battery packs

4.2 온도 불균형 배터리 팩 검출 결과

배터리 팩의 파라미터는 OCV 회복 구간을 사용하여 추출하였다. 온도 균형 배터리 팩과 온도 불균형 배터리 팩의 추출 파라미터는 Fig. 7과 같다. 저항 성분의 경우, 대부분의 SOC 영역에서 온도 불균형 배터리 팩이 온도 균형 배터리 팩보다 큰 값을 보였다. 온도 균형 배터리 팩과 온도 불균형 배터리 팩의 전 영역에서 저항 값 평균은 오믹 저항이 각각 12.67 mΩ, 12.53 mΩ이며, 분극 저항이 각각 8.29 mΩ, 7.73 mΩ 이다. 2가지 배터리 팩 사이의 편차는 온도 균형 배터리 팩이 불균형 배터리 팩 대비 오믹 저항이 1.1 %, 분극 저항이 6.7 % 크게 나타난다. 배터리 센 단위 추출(오믹 저항 7.2 %, 분극 저항 39 %)과 비교하였을 때, 배터리 팩 단위의 저항 차이가 적어졌다. 그 이유는 병렬 합성 저항은 각 저항의 역수를 합한 것이 전체 저항 값의 역수가 되기 때문이다.

Fig. 7

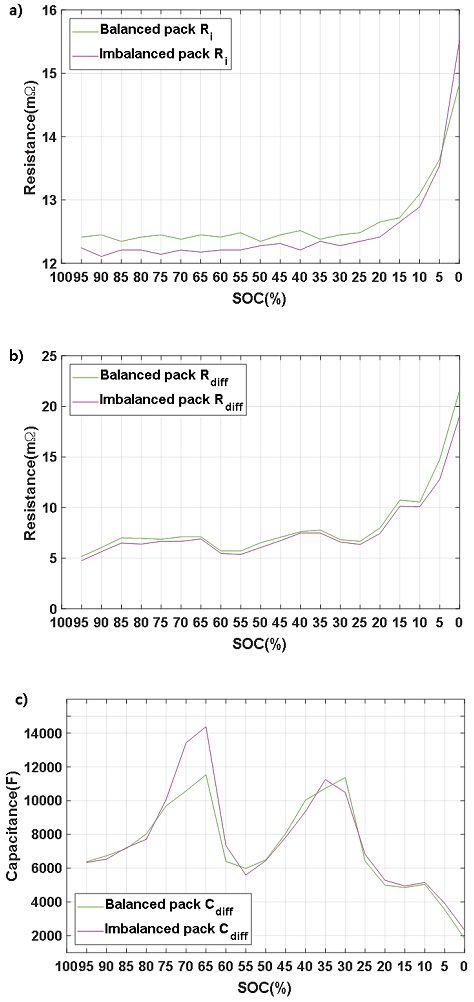
Battery pack level parameters from balanced pack and imbalanced pack using OCV recovery section. a) Ohmic resistance, b) Diffusion resistance, c) Diffusion capacitance

분극 캐패시터 값은 SOC 65 %와 70 % 구간에서 온도 불균형 배터리 팩이 온도 균형 배터리 팩 대비하여 각각 24.6 %, 26.9 % 크게 추출되었다. 다른 SOC 영역 편차의 평균인 0.7 %에 비해 큰 폭의 편차가 발생하였다. 2장의 배터리 셀 단위 파라미터 추출 결과와 유사한 경향으로 추출되었다.

5. 고 찰

본 실험의 온도 불균형 배터리 팩 캐패시터 값이 특정 영역에서 온도 균형 배터리 팩의 값보다 커지는 이유는 다음 2가지로 설명할 수 있다.

첫 번째는 배터리 셀 단위 거동의 반영이다. 배터리 셀 단위 시험 결과와 유사한 구간에서 캐패시터 값의 차이가 발생한 것으로 보아 배터리 셀 단위 파라미터가 영향을 미친 것으로 판단된다. 병렬 배터리 팩에서 합성 캐패시터 값은 각 배터리 셀의 캐패시터 값의 합이다. 따라서 배터리 셀의 거동이 배터리 팩의 거동에 영향을 미친다.

두 번째는 순환전류이다. 병렬 배터리 팩에서의 전압 거동은 배터리 셀 단위보다 복잡하다. 병렬 배터리 팩 내의 특정 배터리 셀의 온도가 높으면, 내부 저항이 작아지며, 그로 인해 전류 불균형이 나타난다.⁹⁾ 전류 불균형은 배터리의 SOC 편차를 일으킨다. 동일 셀, 동일 노화 상태일 때, SOC편차는 곧 OCV의 편차이다. 이와 같은 원리로 3장의 배터리 셀 단위 실험 결과와 같이 캐패시터 성분에 의해 전압 회복 속도가 차이를 보이면 각 배터리 셀의 종단 전압의 편차가 발생한다. 따라서 휴지 중 병렬 배터리 팩 내에 순환전류가 발생하게 되며, 배터리 팩의 전압 거동에 영향을 미친다. 병렬 배터리 팩 내의 고온 배터리 셀의 특성에 의해 특정 SOC 구간에서 전압 회복 속도가 늦어지며 위에서 설명한 병렬 배터리 팩의 내부에 순환 전류를 발생시키는 것으로 판단된다. 그리고 이런 요인에 의해 SOC 65 %와 70 % 구간에서 병렬 배터리 팩의 전압 회복 속도를 늦추면서 결과적으로 캐패시터 값에 영향을 미치는 것으로 판단된다.

6. 결 론

• 1) 배터리 병렬 팩에서 온도 불균형을 검출 할 수 있는 파라미터 산출 방식은 종단 전압이 OCV까지 회복되는 OCV 회복 곡선을 이용한 파라미터 산출이다.
• 2) OCV 회복 곡선을 통해 추출한 파라미터 중, 분극 캐패시터 값을 통해 병렬 배터리 팩의 온도 불균형을 검출 할 수 있다.
• 3) 위의 온도 불균형 검출은 실험에 사용된 배터리 셀의 경우, SOC 65~75 % 구간의 특성을 이용하여 구할 수 있다.

본 논문은 병렬 배터리 팩에서 온도 불균형에 의한 등가회로 모델 파라미터의 변화를 통해 온도 불균형 상황을 진단할 수 있는 방법 연구이다. 실험에서 사용된 배터리 셀의 경우, SOC 65~70 % 구간의 OCV 회복 구간을 사용하여 추출한 캐패시터 값을 통해 온도 불균형을 진단할 수 있다. 이런 결과는 배터리의 전압 회복 동적 특성에 기인하며, 전기 화학적인 요인이 영향을 미치는 것으로 판단된다. 전기적 등가 회로 모델에서 캐패시터에 해당하는 것은 EDL이며, OCV 회복 전압 거동에 영향을 미친다. 따라서 EDL에 대한 연구를 통하여 온도 불균형 상태를 검출할 수 있는 연구가 지속되어야 한다. 또한 온도 불균형 상태 검출은 배터리의 퇴화, 효율, 안전성을 향상 시킬 수 있는 중요한 인자로 본 논문의 연구를 통해 배터리 성능 향상에 기여하길 기대한다.

Acknowledgments

본 연구는 한국전력공사의 2021년 선정 기초연구개발 과제 연구비(R21XO01-3)와 2021년도 정부(산업통상자원부)의 재원으로 한국에너지기술평가원의 지원(20210501010020)을 받았습니다.

References

• N. S. Spinner, C. T. Love, S. L. Rose-Pehrsson and S. G. Tuttle, “Expanding the Operational Limits of the Single-point Impedance Diagnostic for Internal Temperature Monitoring of Lithium-ion Batteries,” Electrochimica Acta, Vol.174, pp.488-493, 2015. [https://doi.org/10.1016/j.electacta.2015.06.003]
• G. Guo, B. Long, B. Cheng, S. Zhou, P. Xu and B. Cao, “Three-dimensional Thermal Finite Element Modeling of Lithium-ion Battery in Thermal Abuse Application,” Journal of Power Sources, Vol.195, No.8, pp.2393-2398, 2010. [https://doi.org/10.1016/j.jpowsour.2009.10.090]
• F. Feng, S. Teng, K. Liu, J. Xie, Y. Xie, B. Liu and K. Li, “Co-estimation of Lithium-ion Battery State of Charge and State of Temperature based on Ahybrid Electrochemical - Thermal - Neural - Network Model,” Journal of Power Sources, Vol.455, Article 227935, 2020. [https://doi.org/10.1016/j.jpowsour.2020.227935]
• M. Fleckenstein, O. Bohlen, M. A. Roscher and B. Bäker, “Current Density and State of charge Inhomogeneities in Li-ion Battery Cells with LiFePO4 as Cathode Material Due to Temperature Gradients,” Journal of Power Sources, Vol.196, No.10, pp.4769-4778, 2011. [https://doi.org/10.1016/j.jpowsour.2011.01.043]
• B. Wang, C. Ji, S. Wang, J. Sun, S. Pan, D. Wang and C. Liang, “Study of Non-uniform Temperature and Discharging Distribution for Lithium-ion Battery Modules in Series and Parallel Connection,” Applied Thermal Engineering, Vol.168, 2020. [https://doi.org/10.1016/j.applthermaleng.2019.114831]
• G. Zhang, C. E. Shaffer, C. Wang and C. D. Rahn, “Effects of Non-uniform Current Distribution on Energy Density of Li-ion Cells,” Journal of The Electrochemical Society, Vol.160, No.11, pp.A2299-A2305, 2013. [https://doi.org/10.1149/2.061311jes]
• E. Hosseinzadeh, S. Arias, M. Krishna, D. Worwood, A. Barai, D. Widanalage and J. Marco, “Quantifying Cell-to-cell Variations of a Parallel Battery Module for Different Pack Configurations,” Applied Energy, Vol.282, 2021. [https://doi.org/10.1016/j.apenergy.2020.115859]
• P. Kumar, D. Chaudhary, P. Varshney, U. Varshney, S. M. Yahya and Y. Rafat, “Critical Review on Battery Thermal Management and Role of Nanomaterial in Heat Transfer Enhancement for Electrical Vehicle Application,” Journal of Energy Storage, Vol.32, Article 102003, 2020. [https://doi.org/10.1016/j.est.2020.102003]
• M. Fleckenstein, O. Bohlen, M. A. Roscher and B. Baker, “Current Density and State of Charge Inhomogeneities in Li-ion Battery Cells with LiFePO4 as Cathode Material Due to Temperature Gradients,” Journal of Power Sources, Vol.196, No.10, pp.4769-4778, 2011. [https://doi.org/10.1016/j.jpowsour.2011.01.043]
• X. Liu, W. Ai, M. Naylor Marlow, Y. Patel and B. Wu, “The Effect of Cell-to-cell Variations and Thermal Gradients on the Performance and Degradation of Lithium-ion Battery Packs,” Applied Energy, Vol.248, pp.489-499, 2019. [https://doi.org/10.1016/j.apenergy.2019.04.108]
• X. Shen, B. Sun, H. Qi, X. Shen and X. Su, “Research on Peak Power Test Method for Lithium Ion Pattery,” Energy Procedia, Vol.152, pp.550-555, 2018. [https://doi.org/10.1016/j.egypro.2018.09.209]
• S. H. Park, J. Park, M.-H. Ryou and Y. M. Lee, “Sensitivity of Power of Lithium-ion Batteries to Temperature: A Case Study using Cylindrical- and Pouch-type Cells,” Journal of Power Sources, Vol.465, 2020. [https://doi.org/10.1016/j.jpowsour.2020.228238]
• J. Luo, J. Peng and H. He, “Lithium-ion Battery SOC Estimation Study Based on Cubature Kalman Filter,” Energy Procedia, Vol.158, pp.3421-3426, 2019. [https://doi.org/10.1016/j.egypro.2019.01.933]
• A. Farmann and D. U. Sauer, “A Study on the Dependency of the Open-circuit Voltage on Temperature and Actual Aging State of Lithium-ion Batteries,” Joural of Power Sources, Vol.347, pp.1-13, 2017. [https://doi.org/10.1016/j.jpowsour.2017.01.098]
• R. Kant and M. B. Singh, “Generalization of the Gouy-Chapman-Stern Model of an Electric Double Layer for a Morphologicallycomplex Electrode: Deterministic and Stochastic Morphologies,” Physical Review E, Vol.88, No.5, Paper No.052303, 2013. [https://doi.org/10.1103/PhysRevE.88.052303]
• X. Lai, C. Jin, W. Yi, X. Han, X. Feng and Y. Zheng, “Mechanism, Modeling, Detection, and Prevention of the Internal Short Circuit in Lithium-ion Batteries: Recent Advances and Perspectives,” Energy Storage Materials, Vol.35, pp.470-499, 2021. [https://doi.org/10.1016/j.ensm.2020.11.026]