GRU 배터리 모델 기반 SOC 추정기 설계

1. 서 론

배기가스 규제 등으로 인해 배터리의 활용으로 연료의 사용량을 감소시킬 수 있는 전기 자동차에 대한 관심이 증가하면서, 배터리로 차량을 구동하기 위한 효율적인 배터리 관리 시스템(Battery Management System, BMS)에 대한 관심이 증가하고 있다.¹⁾ 효율적인 BMS를 위하여 정확한 배터리의 잔존 용량(State of Charge, SOC)을 파악해야 한다. SOC는 일반적으로 측정된 전류 및 전압을 통해 역으로 추정된다.^2,3)

기존 SOC 추정 방법으로는 측정 전압을 활용한 개방 회로 전압(Open circuit voltage) 방식과 측정 전류를 활용한 전류 적분법(Coulomb counting) 방식이 있다.³⁾ 개방 회로 전압 방식은 미리 구축된 전압-SOC 관계를 이용하므로 가장 단순하지만 전압과 SOC 관계가 함수로 성립됨이 보장되어야 하며, 배터리가 화학적으로 안정되어 있는 상태여야 하는 등 제한 조건이 많으며 실시간으로 SOC를 추정하는데 적합하지 않다.⁴⁾ 전류 적분법은 배터리를 통과하는 전류를 적분하므로 실시간으로 SOC를 추정할 수 있지만 오차 누적으로 인하여 장 시간에 대하여 SOC의 정확성을 보장하지 못한다.

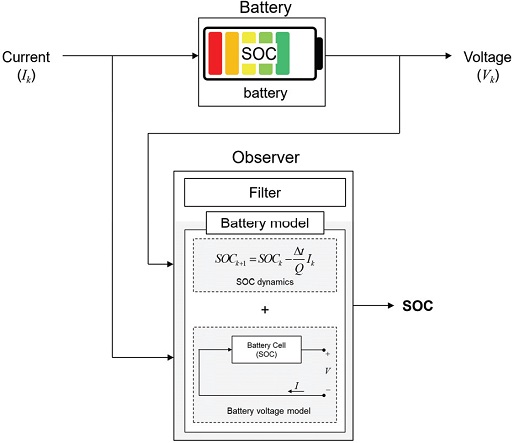
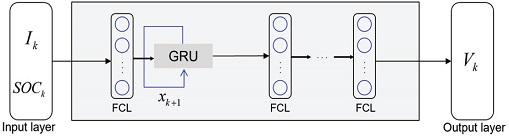
기존 SOC 추정 방식의 단점을 보완하기 위하여 현재 SOC 추정을 위한 주류 연구들은 Fig. 1과 같이 배터리 전압 모델을 설계하고 관측기에 적용하는 방식이다.^2,3,5-7) 이 때 배터리 전압 모델이 정확할수록 SOC는 더욱 정확하게 추정된다. 배터리 전압 모델은 배터리의 전기적 혹은 화학적 특성을 이용하여 설계된다. 그러나 배터리의 특성은 너무 복잡하며, 온도, 화학적 변화, 노화 등과 같은 외관을 고려할 경우 복잡성은 더욱 커진다. 이러한 모델의 복잡성은 SOC 추정에 위한 많은 계산을 요구한다. 그러므로 배터리 전압 모델을 간략하게 1차 혹은 2차 시스템의 등가회로 모델로 설계하고, 이를 SOC 추정을 위한 관측기에 적용하는 방식이 주로 사용된다.⁸⁾

Fig. 1

Scheme of battery model-based SOC estimation

최근에는 기계학습 및 딥 러닝 기술이 발전함에 따라 측정 가능한 데이터, 전압 및 전류를 활용하여 SOC를 추정하는 방식이 연구되고 있다.^5,6) 데이터 기반 SOC 추정 방식은 배터리에 대한 사전 지식이 요구되는 물리적 모델의 설계 및 관측기의 사용 없이 측정된 데이터와 SOC 간의 관계를 학습시킴으로써 모델 정확성에 대한 영향을 제거할 수 있고, SOC에 영향을 끼치지만 모델로 설계할 수 없는 변수들을 고려할 수 있다는 장점이 있다. 하지만 데이터 기반 SOC 추정 방식은 데이터와 SOC 간의 관계가 함수로 보장되어야 하며 훈련된 데이터 범위를 벗어난 데이터가 측정될 경우 SOC의 추정 정확도는 보장할 수 없다.

본 논문은 데이터 기반으로 설계된 배터리 전압 모델을 관측기 중 무향 칼만 필터(Unscented Kalman Filter, UKF)에 적용하여 SOC를 추정하는 방식을 제안함으로써 물리적 모델을 기반으로 관측기를 통해 SOC를 추정하는 방식과 데이터 기반 SOC 추정 방식 각각의 단점을 보완하고자 한다. 이 때, 배터리 전압 모델은 배터리의 시간적 변화를 학습하기 위해 시간의 흐름에 따라 변화하는 데이터를 학습시키는데 적절한 Recurrent Neural Network (RNN) 중 Gated Recurrent Units(GRU)를 사용하여 설계한다. 데이터 기반 배터리 전압 모델 설계는 배터리의 복잡한 사전 지식 및 배터리 성능을 변화시키는 요소들에 대한 정확한 매개변수를 고려하지 않고 배터리 전압 모델의 정확성을 향상시킬 수 있다. 또한 데이터로부터 SOC를 직접적으로 추정하는 방식보다 배터리로 유입 및 유출된 전류와 전압 간의 관계는 모델, 즉 함수 관계로 명확히 정의되므로 모델 설계가 더 용이하다. 제안하는 방식은 물리적 배터리 전압 모델 기반으로 SOC를 추정하는 방식과 비교하여 성능을 검증한다.

2. 배터리 전압 모델 설계

배터리 내부 상태는 배터리에 가해진 전류와 전류에 따라 변화하는 SOC에 따라 결정되며, 변화된 상태는 측정된 전압으로부터 추정하여야 한다. 따라서 배터리 전압 모델은 다음과 같이 설계된다.

이 때 x_k는 배터리의 내부 상태, u_k는 배터리에 인가된 입력, 즉, 전류 I_k이며, d_k는 배터리의 내부 상태에는 영향을 미치나 전류와 달리 제어가 불가능한 변수인 배터리의 SOC를 의미한다. y_k는 관측 가능한 측정, 즉, 전압 V_k이다. f_v(⋅)는 인가된 전류 I_k에 대한 배터리의 동적 시스템 모델이며 h_v(⋅)는 배터리 내부 상태와 전압 간의 대수 관계식이다. 일반적인 배터리 전압 모델 설계 방식은 물리적인 전기적 또는 화학적으로 설계하지만 제안하는 배터리 전압 모델 설계 방식은 전류 및 전압 데이터를 통해 식 (1)을 모사하는 것이다. 이 장에서는 두 가지 모델을 제안한다. 첫 번째 모델은 기존에 널리 사용되는 등가 회로 기반 모델이고, 두번째 모델은 본 연구의 주 방법론인 데이터 기반 모델인 RNN-GRU 기반 배터리 전압 모델이다. 등가 회로 기반 모델은 제안하는 방법론과 비교 검증을 위한 기본 모델로 사용된다.

2.1 등가 회로 기반 모델

가장 정확한 배터리 전압 모델은 전기화학적 모델(Electrochemical model)로써 배터리의 전기적, 화학적 구조를 설계한 것이다. 하지만 배터리 구조의 복잡성으로 인해 SOC 추정에는 적합하지 않다. 반면 등가 회로 모델(Equivalent circuit model)은 전기화학적 요소들을 전기적 요소로만 간략화 한 것이다.⁹⁾ 등가 회로 모델은 배터리를 단순한 식으로 표현 가능하며, 각 전기적 요소들의 매개변수를 실험적으로 정의함으로써 신뢰성을 높인다. 따라서 SOC를 추정할 때 등가 회로 모델이 일반적으로 사용된다. 다만 시스템을 표현하는데 사용된 변수의 개수가 적고 정확한 수치를 알기 힘들기 때문에 모델 정밀도 향상에는 한계가 있다.

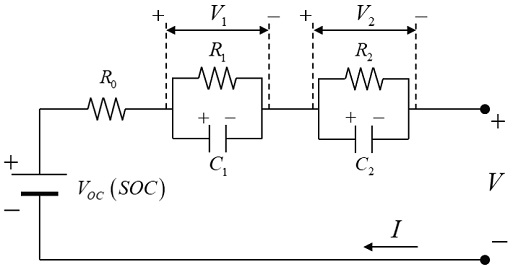
본 논문은 Fig. 2와 같이 분극 저항-분극 축전기 쌍으로 이루어진 셀 두개와 내부 저항 R₀로 구성 되어있는 2차 RC 등가 회로 모델을 기본 모델로 사용한다.¹⁰⁾ 이때 R₁, R₂는 각 셀의 분극 저항이며 C₁, C₂는 각 셀의 분극 축전기의 정전용량이다. V₁, V₂는 각 셀의 분극 현상에 의한 분극 전압이다. V_OC는 개방 회로 전압이며 이는 SOC에 대한 함수이다. I는 인가된 개방 회로 전류이며, V는 부하 전압이다. 2차 RC 등가 회로는 키르히호프의 전류 법칙(Kirchhoff’s Current Law)을 통해 설명할 수 있으며 이를 식 (1)과 같이 정리하면 다음과 같다.

$\[ \begin{array}{c}{x}_k={\left[\begin{array}{cc}{V}_{1,k}, & V_{2,k}\end{array}\right]}^T,\hfill \\ u_k=I_k, y_k=V_k,\hfill \\ f_v\left(x_k,u_k,d_k\right)=\left[\begin{array}{cc}\alpha & 0\\ 0& \beta \end{array}\right]x_k+\left[\begin{array}{c}{R}_1\left(1-\alpha \right)\\ R_2\left(1-\beta \right)\end{array}\right]I_k,\hfill \\ h_v\left(x_k,u_k,d_k\right)=V_{OC}\left(d_k\right)+\left[\begin{array}{cc}-1& -1\end{array}\right]x_k-R_0\cdot I_k,\hfill \\ \begin{array}{cc}\alpha =e^{\frac{\mathrm{\Delta }t}{R_1{C}_1}},& \beta =e^{\frac{\mathrm{\Delta }t}{R_2{C}_2}},\end{array}\hfill \end{array} \]$

(2)

Fig. 2

Second-order RC equivalent circuit model

이때, Δt는 단위 이산 시간이며, 배터리의 SOC는 V_OC에 내포되어 있다.

2.2 RNN-GRU 기반 배터리 전압 모델

제안하는 데이터 기반 배터리 전압 모델은 인가한 전류에 대한 배터리 응답인 전압 데이터를 인공 신경망으로 학습시켜 구현한다. 데이터와 인공신경망으로 모델을 설계할 때 가장 큰 장점은 등가 회로 모델과 달리 상태 변수 x_k에 대한 사전 정의없이, 인공신경망의 구조를 이용하여 상태 변수에 영향을 미치는 입력들, u_k와 d_k 간의 관계를 학습하여 출력 y_k을 모사할 수 있다는 것이다. 배터리 전압 모델의 인공신경망 구조는 배터리의 동적 특성을 모사하기 위한 Recurrent Neural Network(RNN) 종류 중 하나인 Gated Recurrent Units(GRU)를 기반으로 한다.

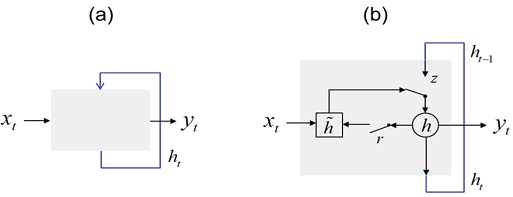
입력층부터 출력층까지의 유닛들이 한 방향성으로 연결된 일반적인 신경망과 달리, RNN은 Fig. 3의 (a)와 같이 유닛들의 연결이 순환적 구조를 가진다. 이러한 구조는 마치 식 (1)의 f_v(⋅)과 같은 시변 동적 모델처럼 유닛들이 시간에 따라 연계된 형태로서, 시계열 데이터의 경향성을 분석하여 시변 동적 모델을 모사할 수 있다.¹¹⁾ 하지만 단순 RNN은 입력 데이터가 유닛을 거치면서 일부 정보가 계산 단계마다 소실되어, 앞쪽의 시간 단계 정보가 뒤쪽의 시간까지 충분히 전달되지 않는 장기 의존성(Long-term dependency) 문제를 가진다는 단점이 있다.

Fig. 3

Structure of RNN and GRU: (a) RNN and (b) GRU

GRU는 Fig. 3의 (b)에서 보이는 것처럼 Reset gate(r_t)와 Update gate(z_t)를 통해 과거와 현재 정보의 반영 정도를 조절하여 장기 의존성 문제를 해결한 RNN 모델이다.¹²⁾ 네트워크에 입력되는 데이터 x_t에 대하여 GRU 모델의 출력 y_t은 다음과 같이 나타난다.

$\[ \begin{array}{c}{y}_t=h_t,\hfill \\ h_t=\left(1-z_t\right)*h_{t-1}+z_t*{\tilde{h}}_t,\hfill \\ {\tilde{h}}_t=\tanh \left(W\cdot \left[\begin{array}{cc}{r}_t*h_{t-1},\hfill & x_t\hfill \end{array}\right]\right),\hfill \\ z_t=\sigma \left(W_z\cdot \left[\begin{array}{cc}{h}_{t-1},\hfill & x_t\hfill \end{array}\right]\right),\hfill \\ r_t=\sigma \left(W_r\cdot \left[\begin{array}{cc}{h}_{t-1},\hfill & x_t\hfill \end{array}\right]\right),\hfill \end{array} \]$

(3)

이 때, z_t 와 r_t는 0에서 1사이의 값으로 과거와 현재 정보의 반영 비율을 조절한다.

충분한 과거 시간 단계 정보까지 고려하여 시계열 데이터의 경향성을 파악하는 GRU를 기반으로 설계한 배터리 전압 모델의 구조는 다음과 같다.

$\[ \begin{array}{c}{u}_k=I_k,d_k=SO{C}_k,y_k=V_k,\hfill \\ f_v\left(x_k,u_k,d_k\right)=FCL\to GRU,\hfill \\ h_v\left(x_k,u_k,d_k\right)=FCL,\hfill \end{array} \]$

(4)

이때, 상태 변수 x_k는 배터리 내부 상태로써 따로 정의될 필요가 없다.

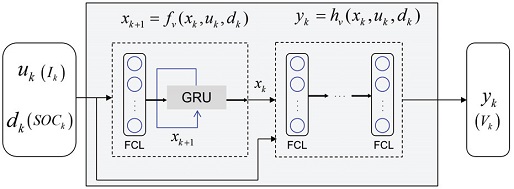
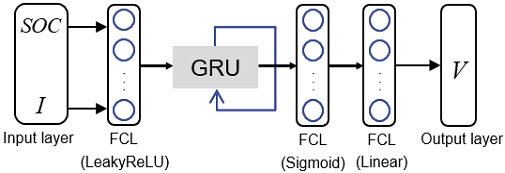
제안하는 배터리 전압 모델의 시변 동적 모델 f_v(⋅)은 FCL와 GRU의 연결로 구성된다. FCL은 동적 모델을 구사하기 전, 동 시간 때 인가되는 전류 I_k와 배터리 SOC SOC_k간의 대수적인 관계를 정의하기 위함이다. 그리고 GRU를 통해 내부 상태 x_k를 모사한다. 배터리 전압 모델의 관측 모델 h_v(⋅)는 여러 개의 FCL들의 연결들로 구성되며, 이는 배터리 내부 상태 x_k와 출력인 전압 V_k간의 대수적인 관계를 모사한다. Fig. 4는 설계된 배터리 전압 구조를 보여준다.

Fig. 4

Proposed battery voltage model

설계된 배터리 전압 구조를 실제 데이터를 이용하여 학습할 때는 Fig. 5와 같이 전류 I_k와 배터리 SOC SOC_k를 FCLs → GRU → FCLs 인공 신경망 구조에 입력하면 전압 V_k가 출력되도록 한다.

Fig. 5

Training structure for the proposed battery voltage model

3. SOC 추정을 위한 무향 칼만 필터 설계

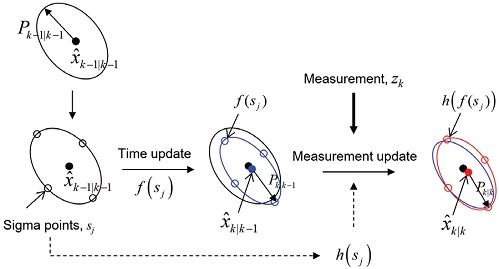
배터리 전압 모델을 이용하여 배터리 SOC를 추정함에 있어, 상태 관측기 중 가장 대표적인 칼만 필터 중 비선형성 시스템 및 관측 모델에 적용하기 위한 응용 버전인 확장된 칼만 필터(Extended Kalman Filter, EKF)이 사용된다.^7,9-10) 그 이유는 SOC와 전류와의 관계는 선형으로 근사 가능하지만 SOC와 전압간의 관계는 비선형성이 커서 선형으로 근사하지 못하기 때문이다. 하지만 EKF의 경우, 시스템을 매순간 편미분을 통해 선형근사를 해야한다는 단점이 있다. 반면, 또 다른 비선형 모델을 위한 칼만 필터인 무향 칼만 필터(Unscented Kalman Filter, UKF)는 실시간 선형근사를 요구하지 않아 신경망 기반 배터리 전압 모델과 같이 비선형성이 큰 시스템의 상태를 추정하기에 적절한 관측기이다.¹³⁾ 무향 칼만 필터는 Fig. 6과 같이 시그마 포인트 s_j라 불리는 실제 상태 x를 대표할 수 있다고 판단되는 평균 주변의 샘플 포인트들을 시스템 모델 f(⋅)과 관측 모델 h(⋅)에 통과시켜 새로운 평균 및 공분산 추정 값을 계산하여 다음 단계의 상태 값을 추정한다.

Fig. 6

Unscented Kalman filter

무향 칼만 필터로 배터리의 SOC를 추정하기 위한 배터리 모델은 다음과 같다.

이때, X_k는 추정해야하는 상태 변수 배터리 SOC와 배터리 전압 모델에서 지정된 상태 변수 x_k의 그룹, 즉 [SOC_k, x_k]^T을 의미하며, u_k는 인가된 전류 I_k, y_k는 측정된 전압 V_k를 의미한다. 그리고 SOC를 위한 시스템 모델 f(⋅)은 다음과 같이 간단한 전류 적분법(Coulomb counting)으로 설계된다.

이때 Q는 배터리 셀의 내부 용량이다. 배터리 전압 모델의 내부 상태 x_k와 관련된 시스템 모델 및 관측 모델 h(⋅)은 설계된 등가 회로 모델 식 (2) 혹은 RNN-GRU 기반 배터리 전압 모델 식 (4)로 정의된다. 따라서 제안하는 SOC 추정을 위한 무향 칼만 필터의 알고리즘은 다음과 같다.

• - 초기 파라미터 결정: 초기 SOC(SOC_0|0), 초기 SOC 오차 공분산(P_0|0), 모델 오차 공분산(Q_k), 전압 센서 오차 공분산(R_k), 시그마 포인트들의 가중치를 결정하는 매개변수(α, κ).
• - 시그마 포인트 s_j 지정 및 시그마 포인트의 가중치 $$ W_j^a$$, $$ W_j^c$$ 결정:

• where

• - Time update:

• where

• - Measurement update:

• where

• - 추정된 $$ \mathrm{S}\mathrm{O}\mathrm{C}=S\widehat{O}{C}_{k\left|k\right.}$$.

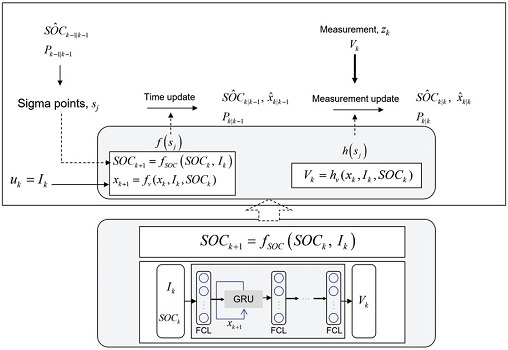
이때 L은 추정하고자 하는 변수의 개수로 1이다. Fig. 7은 제안된 RNN-GRU 기반 배터리 전압 모델을 사용한 SOC 추정 알고리즘을 도식화한 것이다.

Fig. 7

Proposed concept for SOC estimation

4. 검증 결과

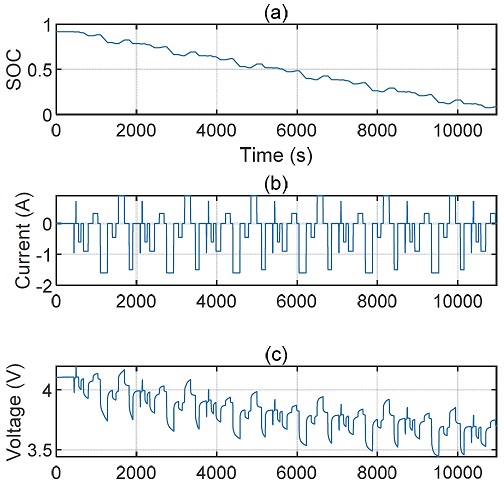
개발된 알고리즘은 0.91 Ah 리튬 이온 배터리를 이용하여 검증한다. Fig. 8은 리튬 이온 배터리의 SOC를 90 % 근처의 범위에서 시작하여 0.1 % 근처까지 방전을 총 10,966초 수행하여 얻은 배터리 데이터이다. 이 때 방전을 위한 전류 프로파일은 임의로 설정하였으며, 전류를 정밀히 측정하여 전류 적분법을 통해 최대한 정확한 SOC를 추정하였다. Fig. 8 (a), (b), (c)는 차례대로 SOC, 인가한 전류 프로파일, 그리고 측정된 전압 데이터를 보여준다. 신호들은 0.1초 단위로 측정되었다. 즉 Δt는 0.1이며 GRU는 4초 동안의 시퀀스 데이터를 입력받는다. 획득한 데이터로부터 배터리 전압 모델을 구축하고 이를 기반으로 SOC 추정 알고리즘을 검증한다.

Fig. 8

Battery data for algorithm validation. (a) SOC, (b) current profile, and (c) voltage

4.1 배터리 전압 모델 검증

SOC 추정을 위한 2차 RC 등가 회로 모델을 설계하기 위해서는 회로를 구성하는 매개변수, 즉 [V_OC(SOC), R₀, R₁, R₂, C₁, C₂]^T, 들이 사전에 요구된다. 우선 배터리에 0 A로 인가하였을 때의 실험적 데이터를 통해⁴⁾ SOC와 V_OC를 Fig. 9 (a)와 같이 정의하였고, Fig. 9의 (b)와 같이 방전 시 획득한 배터리 전압 응답 곡선을 통하여 저항 및 정전 용량들을 Table 1과 같이 추정하였다.¹⁴⁾ 저항 및 정전 용량 추정 시 SOC는 대략 0.9060 – 0.8730 범위 내이다.

Fig. 9

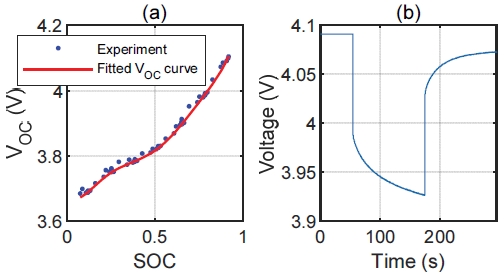
Parameter identification for second-order RC equivalent circuit model. (a) VOC(SOC) and (b) partial enlargement of pulsed discharge voltage for identification of resistance and capacitance

Table 1

Parameters for second-order RC equivalent circuit model

제안하는 RNN-GRU 기반 배터리 전압 모델은 기존의 등가 회로 모델과 달리 매개변수에 대한 지식을 요구하지 않는다. 제안하는 모델은 훈련시키고자 하는 데이터를 모사하기 위해 매개변수를 내부적으로 자동 추정한다. 배터리 데이터를 훈련시키기 위한 RNN-GRU 기반 배터리 전압 모델은 Fig. 10과 같이 동 시간 대 SOC와 전류 간의 관계를 정의하기 위한 1개의 FCL과 f_v(⋅)를 모사하기 위한 GRU 1개, 그리고 h_v(⋅)를 모사하기 위한 2개의 FCL들로 설계하였다. GRU는 과거 40 단계(Time step) 동안의 시퀀스 데이터를 입력으로 받으며 40개의 유닛으로 이루어지도록 설계하였다. FCL들의 활성함수는 각 층의 출력 신호 성질을 기반으로 각각 LeakyReLu, Sigmoid, 선형 함수로 정의하였으며, 각 노드 수는 4, 4, 1개로 설계하였다.

Fig. 10

Designed GRU-based battery model for SOC estimation

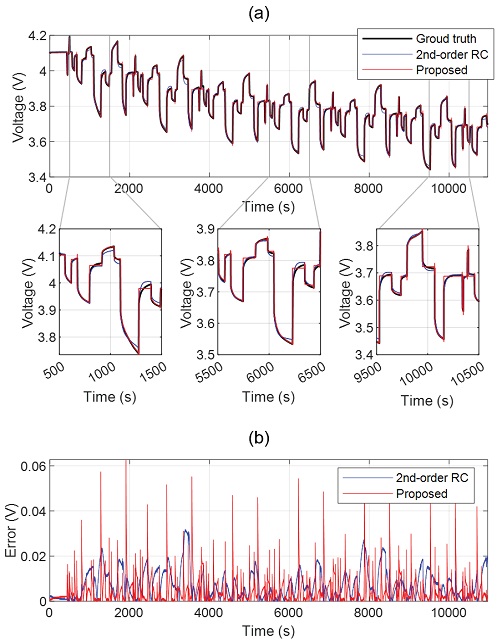
Fig. 11은 인가된 전류에 대해 각 배터리 전압 모델로부터 추출된 전압과 실제 전압과의 오차를 보여준다. 실제 전압은 검은색으로, 2차 RC 등가 회로 모델 기반으로 추출된 전압은 파란색으로, 그리고 제안된 데이터 기반 모델로부터 추출된 전압은 빨간색으로 나타내었다. 두 모델로부터 추출된 전압의 형태는 실제 값과 거의 비슷한 형태를 보이고 있지만 2차 RC 등가 회로 모델의 경우 전압이 급격히 변하는 경우에 오차가 큰 것을 확인할 수 있다. 이는 추정된 매개변수에 대한 부정확성 때문이다. 특히 매개변수는 배터리가 방전될 때를 기반으로 정의되었기 때문에 전류가 양(+)으로 인가되는 경우 그 오차가 더욱 두드러진다.

Fig. 11

Validation of the proposed battery model. (a) voltage and (b) error

제안된 모델의 경우 전압이 급격히 변하는 경우에 대해 2차 RC 등가 회로 모델보다 더 정확도가 높다. 이는 매개변수로 표현되지 않는 다른 배터리의 요소를 신경망 구조가 학습하였기 때문이다. 다만 제안된 모델은 배터리의 전류가 0 A로 인가되는 휴지기나 아주 짧은 시간 동안 전압이 급격히 변할 때 오차가 급격히 커지는데 이는 모델 학습 시 그 현상이 나타나는 데이터의 부족 또는 단순한 신경망 구조로 인해 충분히 학습되지 못했기 때문이다. 그럼에도 불구하고 제안된 배터리 전압 모델은 매개변수에 대한 지식을 요구하지 않으면서도 더 많은 수의 매개변수를 사용할 수 있어, 2차 RC 등가 회로 모델보다 더 정확히 배터리 전압 모델의 복잡성을 모사할 수 있다. 그 성능은 Table 2에 각 모델에 대하여 실제 값과의 오차의 평균값과 표준편차 값으로 나타내었다.

Table 2

Voltage errors with respect to the battery model

4.2 SOC 추정 알고리즘 검증

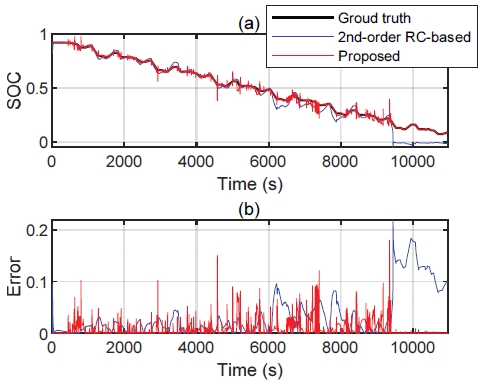
Fig. 12는 각 검증된 배터리 전압 모델을 무향 칼만 필터에 적용하여 SOC를 추정한 결과이다. 이 때 무향 칼만 필터를 위해 적용된 초기값은 다음과 같다.

$\[ \begin{array}{c}SO{C}_{0\left|0\right.}=0.9177,P_{0\left|0\right.}=0.01,\hfill \\ {\mathbf{\text{Q}}}_k={10}^{-7},{\mathbf{\text{R}}}_k={10}^{-3},{\alpha }^2\kappa =5,\hfill \end{array} \]$

Fig. 12

Validation of the proposed SOC estimation algorithm. (a) SOC and (b) error

이 때 2차 RC 등가 회로 기반 SOC 추정을 위해 추가적으로 요구되는 V₁과 V₂에 대한 초기값은 모두 0으로 설정하였다.

Fig. 12(a)는 추정된 SOC이며 (b)는 SOC의 실제값과의 오차이다. 검은색은 실제 SOC, 파란색과 빨간색은 무향 칼만 필터에 각각 2차 RC 등가 회로 모델과 제안된 데이터 기반 모델을 적용했을 때 추정된 SOC를 보여준다. 2차 RC 모델 기반 SOC 추정 방식은 특정 SOC에서 정의된 매개변수로 인해 SOC가 매개변수가 정의될 당시 SOC 범위 내를 벗어날 경우 모델 오차가 커지므로 SOC 추정 결과 성능 또한 하락한다. 이는 특히 약 9,500초 이상, SOC가 약 0.25 밑으로 방전될 때는 거의 제대로 추정하지 못한다. 반면 제안하는 알고리즘은 사전 정의한 매개변수에 대한 영향을 받지 않으므로 SOC 하락에 따른 성능 감소는 거의 보이지 않는다. 하지만 모델 검증 시 나타난 급격한 모델 오차로 인해 SOC 오차 역시 급격히 변한다. 하지만 이는 SOC에 대한 오차 공분산이 감소할수록 감소된다. 따라서 제안된 SOC 추정 알고리즘은 배터리의 매개변수 없이 SOC를 추정할 수 있음을 검증하였고, 그 성능은 매개 변수가 정의될 당시 SOC 범위에서 벗어날수록, 즉 SOC가 완전 방전될수록, 도드라지며 이는 Table 3에 나타난 것처럼 평균적으로 더 나은 결과를 보여준다. 제안하는 배터리 전압 모델은 기본적인 등가 회로 모델보다 더 정확하므로, 모델 오차 공분산 Q_k에 더 신뢰성을 부가하여 무향 칼만 필터 기반 SOC 추정 성능을 향상시킬 수 있다.

Table 3

SOC errors with respect to the battery model in UKF

5. 결 론

본 연구는 데이터 기반으로 배터리 전압 모델을 설계하고 무향 칼만 필터에 설계된 배터리 전압 모델을 적용하여 SOC를 추정하는 알고리즘을 개발한다. 데이터 기반 배터리 전압 모델은 배터리 SOC의 동적 상태 변화를 모사하기 위한 GRU와 SOC와 전압의 관계를 모사하기 위한 FCL의 세트로 이루어져 최종적으로 인가된 전류와 현재 SOC에 대한 전압을 출력한다. 무향 칼만 필터는 SOC의 동적 모델과 개발된 배터리 전압 모델을 기반으로 SOC를 예측한다. 개발된 알고리즘은 SOC 추정 시 가장 대중적으로 사용되는 등가 회로 기반 모델 중 2차 RC 모델 기반 SOC 추정 방식과 비교하였다. 데이터 기반 모델은 파라미터 없이 등가 회로 기반 모델보다 더 나은 성능을 보였으며 이를 기반으로 한 SOC 추정 역시 더 나은 성능을 보여주었다. 이는 데이터 기반 모델이 배터리의 성능에는 영향을 미치지만 매개변수로 표현되지 않는 요소들을 내재적으로 고려하기 때문이다. 따라서 제안된 알고리즘은 배터리의 내부변수에 대한 요구조건없이 SOC를 추정할 수 있다. 다만 현재 데이터 기반 배터리 전압 모델은 알고리즘 가능성 검토를 위해 간단히 설계되었고 하나의 데이터로만 학습되어, 배터리를 완벽히 모사하지는 못한다. 향후 이 부족한 부분을 향상시킬 수 있다면 배터리의 SOC는 배터리의 매개변수 및 다른 복잡한 설계 요소 없이 추정가능할 것이다.

Acknowledgments

이 논문은 부산대학교 4단계 BK21 대학원 혁신사업에 의하여 연구되었음.

References

• E. Meissner and G. Richter, “Battery Monitoring and Electrical Energy Management: Precondition for Future Vehicle Electric Power Systems,” Journal of Power Sources, Vol.116, No.1-2, pp.79-98, 2003. [https://doi.org/10.1016/S0378-7753(02)00713-9]
• M. U. Ali, A. Zafar, S. H. Nengroo, S. Hussain, M. J. Alvi and H. J. Kim, “Towards a Smarter Battery Management System for Electric Vehicle Applications: A Critical Review of Lithium-Ion Battery State of Charge Estimation,” Energies, Vol.12, No.3, pp.1-33, Article No.446, 2019. [https://doi.org/10.3390/en12030446]
• S. Piller, M. Perrin and A. Jossen, “Methods for State-of-charge Determination and their Applications,” Journal of Power Sources, Vol.96, No.1, pp.113-120, 2001. [https://doi.org/10.1016/S0378-7753(01)00560-2]
• C. Weng, J. Sun and H. Peng, “A Unified Open-circuit-voltage Model of Lithium-ion Batteries for State-of-charge Estimation and State-of-health Monitoring,” Journal of Power Sources, Vol.258, pp.228-237, 2014. [https://doi.org/10.1016/j.jpowsour.2014.02.026]
• D. N. T. How, M. A. Hannan, M. S. H. Lipu and P. J. Ker, “State of Charge Estimation for Lithium-Ion Batteries Using Model-based and Data-driven Methods: A Review,” IEEE Access, Vol.7, pp.136116-136136, 2019. [https://doi.org/10.1109/ACCESS.2019.2942213]
• M. Zhang and X. Fan, “Review on the State of Charge Estimation Methods for Electric Vehicle Battery,” World Electric Vehicle Journal, Vol.11, No.1, Article No.23, 2020. [https://doi.org/10.3390/wevj11010023]
• B. Y. Yoon, S. Yoo and S. Seong, “Compensation Method of EKF based on LSTM for Estimating State of Charge of Li-polymer Battery,” Transactions of KSAE, Vol.27, No.7, pp.501-507, 2019. [https://doi.org/10.7467/KSAE.2019.27.7.501]
• R. Xiong, Q. Yu and L. Y. Wang, “Open Circuit Voltage and State of Charge Online Estimation for Lithium Ion Batteries,” Energy Procedia, Vol.142, pp.1902-1907, 2017. [https://doi.org/10.1016/j.egypro.2017.12.388]
• M. H. Jung, J. H. Jeon and S. J. Park, “Development of Impedance-based Equivalent Circuit Model to Predict Current-voltage Behavior for 48 V MHEV NMC Battery,” Transactions of KSAE, Vol.29, No.4, pp.337-348, 2021. [https://doi.org/10.7467/KSAE.2021.29.4.337]
• Z. Huang, Y. Fang and J. Xu, “SOC Estimation of Li-ion Battery based on Improved EKF Algorithm,” Int. J. Automotive Technology, Vol.22, No.2, pp.335- 340, 2021. [https://doi.org/10.1007/s12239-021-0032-4]
• O. I. Abiodun, A. Jantan, A. E. Omolara, K. V. Dada, N. A. Mohamed and H. Arshad, “State-of-the-art in Artificial Neural Network Applications: A Survey,” Heliyon, Vol.4, No.11, 2018. [https://doi.org/10.1016/j.heliyon.2018.e00938]
• J. Chung, C. Gulcehre, K. Cho and Y. Bengio, “Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling,” arXiv preprint arXiv:1412.3555, , 2014.
• S. Julier and J. Uhlmann, “New Extension of the Kalman Filter to Nonlinear Systems,” International Sysmpsium on Aerospace/ Defence Sensing, Simulation and Controls Proceedings, pp.182-193, 1997. [https://doi.org/10.1117/12.280797]
• A. Li, S. Pelissier, P. Venet and P. Gyan, “Fast characterization Method for Modeling Battery Relaxation Voltage,” Batteries, Vol.2, No.2, Article No.7, 2016. [https://doi.org/10.3390/batteries2020007]