기둥측면충돌시험을 고려한 전기자동차 차체 및 배터리 팩 통합 구조물의 비선형동적응답 구조최적설계
Copyright Ⓒ 2021 KSAE / 188-10
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
A nonlinear, dynamic response structural optimization is carried out for a structure that integrates the body-in-white and battery pack of an electric vehicle. The loading conditions are made from a side pole impact test. The objective function is the mass, while the intrusion of the battery pack is defined as a constraint to prevent fires or explosions involving the battery pack during a car accident. An optimization method that uses the equivalent static loads method(ESLM) is proposed. An electrical vehicle(EV) model is generated from an existing crash simulation vehicle model. The proposed method was found to be an effective structural design method for electric vehicles.
Keywords:
Electric vehicle, Battery pack, Crashworthiness, Equivalent static loads method, Structural optimization키워드:
전기자동차, 배터리 팩, 충돌성능, 등가정하중법, 구조최적설계1. 서 론
기둥측면충돌시험을 고려하여 전기자동차(EV, Electric Vehicle)의 배터리 팩(Battery pack)과 차체(BIW, Body-in-White)를 통합한 구조물(Integrated structure)의 구조최적설계(Structural optimization)에 대한 연구가 수행되었다. 배터리를 보호하기 위한 제한조건(Constraints)이 최적설계에서 고려되었다. 비선형동적응답(Nonlinear dynamic response)을 구조최적설계 과정에서 고려하기 위하여 등가정하중법(ESLM, Equivalent Static Loads Method)을 사용했다. 실제 차량의 충돌해석모형을 활용하여 제시한 방법을 적용하고 결과를 검토해본다.
세계 각국에서는 자동차사고로 인한 상해와 사망률을 줄이기 위하여 신차안전도평가를 적용하고 있다. 한국에서도 1999년부터 신차안전도평가(KNCAP, Korean New Car Assessment Program)를 시행하고 있다.1) 충돌시험으로는 정면충돌, 측면충돌, 기둥측면충돌 등이 적용되고 있다. 특히, 기둥측면충돌시험은 기둥에 하중이 크게 집중되므로 만족시키기가 상대적으로 어려우며 한국에는 2010년에 도입되었다. 자동차 설계시에도 충돌시험 조건을 적용해서 외력 및 제한조건 등으로 사용한다. 이러한 제한조건들을 만족시키면서 차체의 경량화를 달성하기 위해 구조최적설계 기법이 활용된다.2,3)
초기의 최적설계 이론은 비선형성(Nonlinearity)이 크거나 규모가 큰 문제(Large scale)일수록 적용하기가 까다로웠다. 이와 같은 문제를 비선형동적응답 구조최적설계(Nonlinear dynamic response structural optimization)라 하며4) 자동차충돌문제는 대표적인 사례이다.비선형동적응답을 최적설계 과정에서 직접 다루지 않고 반응표면기법(RSM, Response Surface Method)5) 등의 근사모형을 활용하는 대안이 있지만 정확도가 높은 모형을 생성하기 위해서는 많은 수의 비선형동적해석이 필요하다. 최근에는 컴퓨터의 성능이 좋아짐에 따라 이러한 방법들도 널리 적용되고 있다.6)
근사모형을 활용하는 방법 외에 비선형동적응답을 직접 최적설계 과정에서 고려하는 방법 중에는 등가정하중법이 있다.7) 등가정하중(ESLs, Equivalent Static Loads)은 비선형 또는 동적해석에서 변위장(Displacement field)과 동일한 변위 응답들을 선형정적해석(Linear static analysis)에서 발생시킬 수 있도록 계산된 복수(Plural)의 하중들을 가리킨다. 이를 활용하면 어려운 비선형동적응답 구조최적설계 문제를 기존에 잘 발전된 선형정적응답 구조최적설계(Linear static response structural optimization) 문제로 변환하여 쉽게 해결할 수 있다. 비용 부담이 크게 줄어들고 본래 문제의 응답을 최적설계 과정에서 고려할 수 있기 때문에 효과적이지만 해당 이론의 학문적 근거에 대해 아직까지 다소 논쟁이 진행되고 있다.8,9)
한편, 전기자동차(EV, Electric Vehicle)는 각종 유해한 배기가스를 배출하지 않는 친환경자동차 중에 하나이며 화석연료(Fossil fuel)를 사용하는 일반자동차의 대안으로 제시되고 있다. 일반자동차의 내연기관들은 에너지 효율이 좋지 않으므로 자원의 효율적인 활용 측면에서도 이롭다. 일반자동차와 비교하여 단점은, 짧은 주행거리, 긴 충전시간, 배터리의 비싼 가격, 배터리 화재나 폭발에 의한 안전성 측면 등이 있다.10) 사고 상황에서 배터리의 화재나 폭발을 지연시키거나 방지하는 것은 탑승자의 생명과 직결되므로 다른 무엇보다도 대단히 중요하다. 다행히도 상술한 구조최적설계와 같은 전통적인 설계만으로도 충돌에 대한 안전성을 효과적으로 향상시킬 수 있을 뿐만 아니라 차량의 경량화와도 연관이 되어 총 주행거리 증가와 연비 향상의 효과도 함께 기대할 수 있다.
그러나 현재 상용화된 전기자동차의 차체는 공신력 있는 특별한 설계 기준이 아직까지 존재하지 않고, 기존에 일반자동차에서 사용되던 차체를 거의 그대로 사용하거나 차량의 전면부 등에서 일부의 변화만 있는 것으로 보인다.11) 배터리 팩은 완성차 업체와 제조사가 다르기 때문에 완성차 업체가 요구하는 사양(Specification)에 맞추어 제조사에서 제작하고 있다. 배터리 팩의 제조사에서 적용하는 별도의 배터리 팩 설계에 대한 안전 기준은 GB/T 등이 있으나, 공인된 국제적 기준도 아니며 자동차사고 상황과는 거리가 멀고 단순한 충격시험만 다루고 있다.12,13) 따라서 차체와 배터리 팩을 통합한 실제 전기자동차는 사고 상황에 대한 안전성이 제대로 보장이 되지 않거나 차체와 배터리 팩 중 하나는 과설계(Overdesigned)가 될 수밖에 없다고 사료된다.14,15) 이에 대한 연구 결과들을 살펴보면 아직 세계적으로도 시작 단계라 할 수준에 머물고 있다.
그러므로 전기자동차의 차체와 배터리 팩의 통합 구조물의 비선형동적응답 구조최적설계 방법이 연구되었다. 하중조건은 충돌시험 중 가장 만족시키기 어렵다고 판단한 기둥측면충돌시험을 적용하였으며, 사고 상황에서 배터리 팩의 안전성을 고려하기 위하여 배터리 팩 안쪽의 침입량(Intrusion)을 제한조건으로 정의했다. 비선형동적응답 구조최적설계 방법으로 등가정하중법을 활용했다. 자동차충돌해석에 활용되는 실제 규모의 유한요소모형을 변경하여 가상의 전기자동차 모형을 생성했고, 이를 활용해서 기둥충돌시험을 고려한 비선형동적응답 구조최적설계 예제를 정의하였다. 제안한 방법을 예제에 적용하고 결과를 도출하였다. 2장에서는 연구 방법과 최적설계 이론으로 등가정하중법을 소개하고, 3장에서는 예제에 사용된 유한요소모형의 제작과정과 이를 활용한 설계 조건 및 방법에 대해 설명한다. 4장에서 구조최적설계 예제의 정식화 및 결과를 설명하고 5장에서 연구내용을 종합하여 결론을 도출한다.
2. 연구 방법 및 배경 이론
2.1 전기자동차의 특성과 배터리 팩 통합 설계
전기자동차 차체와 배터리 팩을 통합하고 설계하여 자동차사고 상황에서 배터리의 안전성을 향상시키는 구조최적설계 방법을 제안한다. 전기자동차의 구조적인 특징은 일반자동차와 전혀 다르기 때문에 일반자동차의 차체는 전기자동차에는 적합하지가 않다. 하지만 현재까지는 전기차 차체에 대한 마땅한 설계의 기준이 제시되지 않고 있다. 기존의 일반자동차에 사용되었던 차체를 소폭 변형하여 사용해왔지만 전기차의 고유한 차체를 설계할 수 있는 새로운 방법이 점차 필요하다. 연구에서는 차체와 배터리 팩을 통합한 하나의 구조물로 취급하여 설계를 수행한다. 그래야만 고유한 전기차의 구조물을 설계하는 것이 된다. 자동차사고 상황에서는 배터리의 안전성도 함께 고려되어야 하기 때문이다.
만약 배터리에 심한 충격이 가해지거나 배터리 모듈이 과도하게 변형될 경우 큰 화재나 폭발의 가능성이 있다. 각종 단자의 접촉불량이나 전해액누수, 단락, 누전 등이 발생하여도 감전이나 발화 및 폭발로 이어질 수 있다.16,17) 리튬배터리의 화재에서 발생하는 불화수소 등의 유독가스도 위협적이다.18) 그러므로 자동차 사고가 발생하면 전기자동차는 일반자동차와 달리 배터리 폭발에 대한 안전성이 추가로 요구된다. 차체와 배터리 팩을 단독으로 설계해서는 이러한 것을 달성할 수 없다.
전기차는 구조적으로도 일반자동차와 차이가 있다. 구동계가 간단하며, 부품의 수가 크게 줄어들고 차량의 전면부에 상당한 공간이 생긴다. 그러나 정면이나 후면에는 배터리를 장착하지 않는다. 정면충돌과 후방충돌 사고를 생각하여 기피되기 때문이다. 전기자동차의 전면부에 대한 재설계는 이미 다수의 연구가 수행되었다.19,20) 결국에 배터리 팩은 주로 차량의 하면부에 장착된다. 그런데 주행거리를 늘리기 위해서는 배터리를 많이 탑재하는 것이 유리하지만, 안전성에서는 오히려 여유공간이 없게 되므로 해로울 수 있다. 특히 차량의 하면부에 배터리 팩을 장착하게 되면 측면충돌로부터 배터리 보호가 상당히 어렵다. 기둥에 의해 하중이 한곳에 집중되는 기둥측면충돌시험은 특히 까다롭다.
한편, KNCAP이 도입되고 교통사고로 인한 사망자가 크게 줄어들었다는 조사결과가 있다.21) 전기차의 설계에서는 정면이나 후면충돌보다 측면충돌이 더 중요하다고 말하는 다른 연구들도 있다.11,22) 그러므로 본 연구에서는 자동차사고상황을 설계에서 직접 고려하였으며 차체와 배터리 팩은 설계 과정 중 하나의 통합 구조물로 다루었다. 여기서 기둥충돌시험은 전기차 배터리 보호의 측면에서 가장 가혹한 조건으로서 채택되었다.
2.2 비선형동적응답 구조최적설계: 등가정하중법
비선형동적응답을 직접 고려할 수 있는 구조최적설계 방법으로 등가정하중법을 소개한다.7) 상술한 대로 자동차충돌해석은 비선형성과 문제의 규모가 크고 동적응답 문제이므로 이를 구조최적설계에서 직접 고려하기가 일반적으로 어렵다. 등가정하중법에서는 비선형동적응답을 활용하지만 선형정적최적설계 알고리즘을 활용하여 문제를 해결한다. 등가정하중이란, 선형정적해석에서 비선형 또는 동적해석과 동일한 변위를 유발하도록 만들어진 정적하중으로 다음과 같이 정의된다.
비선형동적해석을 수행하고 얻어진 여러 시간 간격들 t1, t2, .. , tn에 따른 변위장을 xN(t)이라 하면 등가정하중 feq은 다음과 같이 산출한다.
| (1) |
여기서 KL은 비선형동적해석과 동일한 구조물의 선형정적해석 모형의 강성행렬이다. 한편, 선형정적해석에서 지배방정식은 다음과 같다.
| (2) |
여기서 xL은 선형정적해석에서 변위를 의미하며, 결국 xL = xN이다. 즉, 등가정하중을 외력으로 작용하여 선형정적해석을 수행하면 비선형동적해석에서의 변위장과 동일한 변위가 계산된다.
위에 사용된 선형정적해석 모형을 그대로 다시 활용하여 선형정적응답 구조최적설계를 수행하며 등가정하중을 외력으로 사용한다. 여러 시간 간격들 t1, t2, .. , tn에 대하여 각각의 feq는 위 과정을 통해서 일괄적으로 계산된다. 계산된 등가정하중들은 한번의 최적설계 과정에서 다중하중조건으로 간단히 고려할 수 있다. 그러므로 선형정적응답 구조최적설계에서 비선형동적응답을 하나의 시간만이 아닌 다양한 시간에 대해서도 고려할 수 있게 된다. 여기까지의 과정을 등가정하중법에서는 설계 주기(Design cycle)라 부르며 수렴 조건이 만족하도록 설계 주기를 몇 번 반복하여 해를 얻는다.
설계 주기를 반복하면 변위 제한조건등을 만족시키면서 목적함수가 감소하도록 최적해를 찾아 수렴해가는데, 이러한 주기마다 비선형해석은 단지 한 번만 필요하기 때문에 비선형동적해석 횟수가 상당히 적게 요구된다. 유전알고리즘이나 근사모형을 활용한 최적화 등의 기존의 방법들이 기본적으로 아주 많은 실험의 반복이나 유한요소해석 횟수가 필요한 것과는 커다란 차별성이 있다. 단점으로는 일반적인 등가정하중법이 변위 응답만을 고려하기 때문에 동적해석의 반력이나 응력과 같은 동하중은 고려하기 어려운 것이다. 방법론의 이론적 근거도 여전히 논의가 되고 있다.7,8) 그러나 자동차 충돌 해석과 같은 대규모의 비선형동적응답 문제에서 다양하게 적용되고 발전시킨 연구들23-25)이 활발히 수행되었고 반력과 같은 동하중을 고려할 수 없는 등가정하중법의 단점을 보완하기 위한 방법도 연구되고 있다.24) 다만, 본 연구에서는 일반적인 등가정하중법7)을 활용하였다.
3. 전기자동차의 통합 구조최적설계 방법
3.1 유한요소모형 제작 및 해석
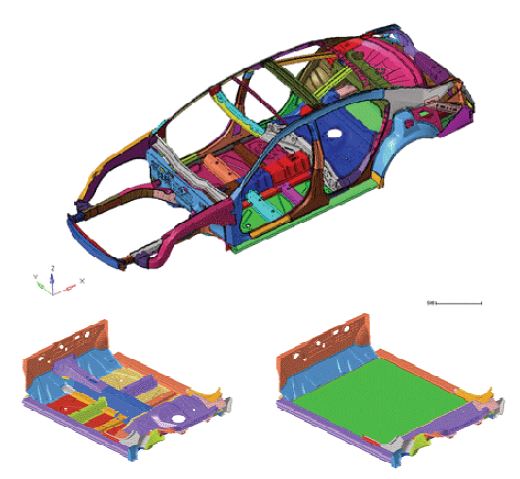
전기차의 설계를 위해 전기자동차의 차체 및 배터리 팩의 유한요소모형이 필요하다. 연구에서는 활용할 수 있는 기존의 전기차 모형이 존재하지 않으므로 직접 모형을 생성했다. 전기차 모형은 기존의 일반적인 내연기관 자동차의 유한요소모형을 수정하고 변경하여 제작했다. 일반 자동차의 유한요소모형으로는 미국도로교통안전국(NHTSA, National Highway Traffic Safety Administration)에서 제공하는 Honda의 Accord의 충돌해석용 모형26)이있다. LSTC사의 비선형동적응답 구조해석 소프트웨어인 LS-DYNA27)의 해석 모형이며 Fig. 1에 나타나 있다. 연구에서는 이 모형을 변경하여 가상의 전기자동차를 제작해 활용한다. 일반 자동차 모형을 어떻게 변경하여 전기차의 차체를 제작할지 참고하기 위해 Tesla의 차량을 비교 및 참고 대상으로 활용했다. 일반적인 현재의 전기차의 차체에 대한 형태를 연구에서 반영하기 위함이다. 비교 모형은 Tesla S의 3DS MAX 모형28)으로 Fig. 2에 나타나 있다. 단, 유한요소해석용 모형이 아니라 단순한 3차원 그래픽 모형이다.
전기자동차의 차체를 제작한 과정을 요약하면 다음과 같다. 엔진, 라디에이터, 변속기, 배기관, 연료통 등을 제거하고 배터리 팩의 모형을 제작하여 장착했다. 그 외의 전기자동차의 부품들은 본 연구에서는 중요도가 낮기 때문에 제조사의 조언을 얻어 점 질량으로 단순화하였다. Fig. 3의 위쪽에 있는 사진과 아래쪽의 왼쪽 사진은 원본 모형의 차체를 보여주고 있다. 차체의 센터플로어를 포함한 하면부와 연료통이 차지하던 공간을 삭제하거나 변형하여 하면부를 평면에 가깝도록 변형하였다. 변형된 후의 모습이 Fig. 3의 아래쪽에서 오른쪽의 사진이다. 이때 변형된 후의 형태는 Fig. 2의 비교 모형과 상당히 유사하다. 기존의 일반자동차의 차체에서는 센터플로어 등이 차량의 강성에 상당한 기여를 하였지만, 전기차에서는 배터리 팩이 이를 대신할 수 있다. 따라서 전기차에서는 차체의 밑바닥을 단순한 형태로 가정했다. 비교 모형을 참고해서 배터리 팩이 장착될 공간의 마련을 위하여 하면부의 높이를 조절하였으며, 배터리 팩이 장착되는 결합부의 형태나 배터리 팩 전체의 길이와 높이 등을 결정하였다.
연구에 사용할 배터리 팩의 유한요소해석 모형은 직접 제작했다. 참고할 만한 기존의 배터리 팩에 대한 유한요소모형이 없기 때문에 제작과정에서는 실존하는 배터리 팩을 참고하였다. 제조사에서 제품의 상세한 사양의 공개를 어려워했기 때문에 인터넷에 공유된 사진들이나 전시 제품의 관찰을 통해 최대한 현실에 가깝게 재구성하였다. 대상 차량의 사이즈에 맞춰서 가로 1563 mm, 세로 2006 mm, 높이 96 mm의 팩을 설계하였으며 차체와 약 10 cm 간격으로 빔 요소를 이용해 결합하였다. 생성된 배터리 팩은 Fig. 4에 나타나 있다. 팩 내부에는 총 30개의 배터리 모듈이 장착되었다. 차체와 배터리 팩을 합하면 전체 전기자동차 모형이 된다.
생성한 유한요소모형은 원본과 마찬가지로 LS-DYNA의 비선형동적해석 모형이다. 등가정하중 계산과 선형정적응답 구조최적설계에서는 Altair사의 OptiStruct29)가 사용되었다. LS-DYNA의 해석 모형을 활용해 OptiStruct의 선형정적해석용 모형도 생성하였다. 접촉의 모사는 등가정하중법에서 일반적으로 사용하는 방법인 스프링연결로 대체하였다. 연구에서는 기존의 전기차 모형이나 설계 데이터를 얻을 수 없었으므로 제작된 모형의 초기 설계를 최적설계 결과와 직접 비교하였다.
3.2 설계 조건 및 방법
생성한 가상의 전기자동차 모형을 활용하여 전기자동차의 차체 및 배터리 팩의 통합 구조물에 구조최적설계를 적용한다. 이를 통해 얻어진 설계는 전기자동차 특성을 반영한 고유의 차체라고 할 수 있다. 상술한 것처럼 배터리의 안전성에 미치는 영향이 가장 좋지 않은 기둥측면충돌시험을 설계에서의 하중조건으로서 고려한다. 차체와 배터리 팩을 동시에 설계 대상으로 고려하므로 설계변수는 사이드실, B-pillar 등의 차체 프레임 두께들과 배터리 팩에 속한 각종 프레임의 두께들이 고려된다.
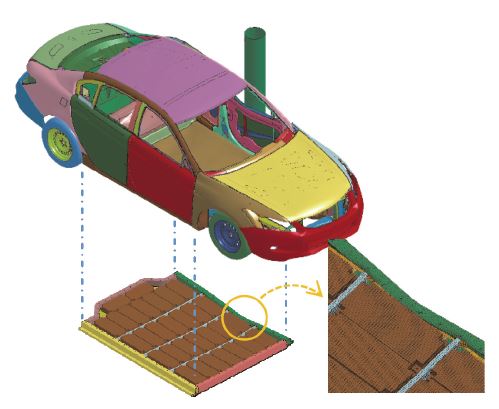
기둥측면충돌시험은 신차의 안전성을 평가하기 위한 방법으로 KNCAP 등에서 수행하는 대표적인 충돌 시험 중 하나이다. 충돌 시험은 정면이나 후면에서도 이뤄지지만 기둥측면충돌시험은 그 중에서 측면으로 기둥에 대하여 차량이 돌진하는 형태로 시험이 진행된다. 이것은 전신주나 가로등에 차량이 균형을 잃고 제동력을 상실한 상태에서 회전하며 돌진하는 상황을 가정한 것이다. 이 때 기둥은 변형이 되지 않고 하중을 좁은 곳에 집중하여 차량에 전달하게 된다. 따라서 조건을 만족시키기가 상당히 까다롭고 탑승자에게 높은 상해 수준을 유발할 수 있는 시험이다. 차량은 기둥과 75도 각도로 기울어져 32 km/h의 속도로 돌진한다. 실차 시험에서는 이러한 조건으로 움직이는 틀 위에 차량을 올려놓고 기둥을 향해 충돌시킨다. Fig. 5는 유한요소해석을 이용하여 기둥측면충돌시험을 수행하는 모습을 나타내고 있다. 차량에 장착된 배터리 팩의 내부가 함께 나타나 있다. 충격에 의해 배터리 팩 내부까지 변형이 발생하고 있다.
기둥측면충돌을 고려한 설계에서는 일반적으로 탑승자의 생존공간확보 등이 제한조건으로 고려된다. 또한 전기자동차의 사고 상황에서 탑승자가 탈출하거나 구조될 수 있도록 최소한 5분 이상의 화재나 폭발을 지연시킬 시간적 여유가 필요하다. 그런데 컴퓨터를 활용한 구조해석에서는 배터리의 발화나 폭발의 가능성을 예측하는 것이 어렵다. 해석 결과를 관찰하여 화재의 발생을 예측할 수 있다고 하더라도 발생 시점은 모른다. 육안으로 변형이 일어난 것을 관찰하면서 전해액의 누수나 단락 및 누전의 발생을 예측하고 화재가 날 수 있음을 짐작할 뿐이다. 예컨대, 날카로운 부분에 의해 배터리 모듈이 파고드는 형태로 변형될 때 화재를 예측하곤 한다. 이러한 방법은 설계자의 경험이나 간접적인 관찰에 의존하기 때문에 최적설계시 설계 조건으로 사용하기는 어렵다. 연구에서는 충돌에 의한 배터리 팩 내부의 변형이 배터리 모듈을 직접 충격하면 해당 부분에서 발화의 가능성이 있다고 가정하였다. 이러한 가정에 따라, 배터리 팩 내부의 배터리 모듈에 직접적인 충격이 가해지지 않도록 설계 조건을 정의했다. 다소 과한 조건으로 보일 수 있는 가혹한 제한조건이지만 만족하기만 한다면 배터리의 화재 확률이 매우 낮아진다. 즉, 배터리 화재를 가장 확실히 방지하기 위한 보수적인 설계 조건이라 할 수 있다. 또한 승객의 탑승공간에 대한 기둥의 침입량을 동시에 제한하므로 탑승자의 생존공간을 자연스럽게 확보할 수 있는 이점도 있다.
구조최적설계 과정에서는 비선형동적응답을 고려하기 위해 등가정하중법을 사용한다. 첫 단계로는 기둥측면충돌에 해당하는 비선형동적해석을 수행한다. 미리 제작해둔 전기자동차의 유한요소모형이 활용된다. 비선형동적해석 결과에서 얻어진 변위 응답을 이용하여 등가정하중을 산출한다. 계산된 등가정하중을 외력으로 사용해 선형정적최적화를 수행한다. 등가정하중법이 동적 변위를 완전히 동일하게 선형정적해석에서 모사하기 때문에 변위 제한조건을 선형정적최적설계에서 그대로 고려할 수 있다. 선형정적최적화가 완료되면 설계변수를 갱신하고 다시 첫 단계로 돌아간다. 수렴할 때까지 이러한 설계 주기를 반복하여 최적해를 얻는다.
한편, 주어진 문제의 침입량은 시간에 따라 연속적으로 변화하는 변위 응답이다. 만약 문제가 수렴하였고 마지막 설계점에서 침입량이 최대가 될 때 제한조건을 만족하면 다른 모든 시간에 대해서도 제한조건을 만족한다. 그러므로 문제에서는 최대침입량이 발생하는 특정 시점만을 고려해도 충분하다. 결론적으로 주어진 문제는 다중하중조건이 아니라 단일하중조건으로도 가능한 문제이다. 매 설계 주기마다 침입량이 최대가 되는 시점을 산출하고 그 시점에서 등가정하중을 계산하고 적용하면 된다.
4. 전기자동차의 구조최적설계 예제
4.1 구조최적설계 정식화
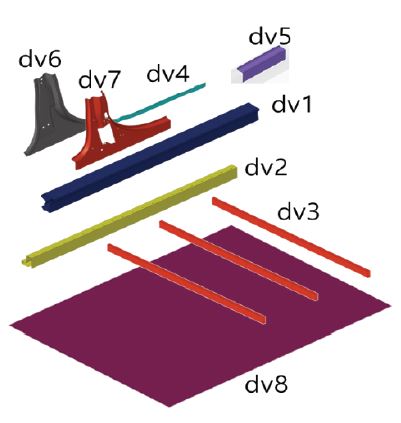
전기자동차의 통합 구조물에 대한 설계 예제를 통해 제안한 방법을 적용해본다. 앞서 생성한 유한요소모형을 사용한다. 외력과 해석조건은 Fig. 5의 기둥측면충돌시험과 동일하다. 차체와 배터리 팩을 통합하여 설계하므로 설계변수는 차체와 배터리 팩에서 모두 선택하였다. Fig. 6는 이러한 설계변수들을 나타내고 있다. 설계변수 2, 3, 8은 배터리 팩의 쉘 부재의 두께, 1, 4, 5, 6, 7은 차체의 쉘 부재의 두께이다. 따라서 주어진 문제는 치수최적설계에 해당한다. 구조최적설계 정식화는 다음과 같다.
| (3) |
bi는 각 설계변수들이고 목적함수는 질량이며, 제한조건은 배터리 팩의 안쪽면에서 측정된 침입량(Intrusion)이다. Fig. 5에 보이는 것처럼 충돌에 의해 배터리 팩 내부에서 배터리 모듈과 접촉이 일어나는데, 접촉을 막기 위해 허용침입량(Intrusion_all)을 정의하여 최대침입량을 제한하였다. 사용된 배터리 팩 모형의 안쪽은 50 mm의 여유 공간을 갖도록 제작되었고 부재의 두께 등을 고려해 허용침입량은 40 mm으로 정의했다. 제한조건이 만족되면 접촉이 발생하지 않으므로 배터리 모듈에 강한 충격에너지가 전달되지 않는다고 할 수 있다. 설계변수의 초기값은 [1.5, 1.5, 1.5, 1.2, 0.6, 1.0, 1.0, 1.5]이고, 하한값 bL은 각각 [1.0, 1.0, 1.0, 0.5, 0.5, 0.5, 0.5, 0.5]이며, 상한값 bU은 각각 [2.0, 2.0, 2.0, 2.0, 1.5, 1.5, 1.5, 2.0]으로 정의하였다. 설계변수의 단위는 모두 mm이다.
정의한 문제에 등가정하중법을 적용하여 최적설계를 수행한다. 기둥측면충돌시험에 대한 비선형동적해석을 Fig. 5와 같이 수행하고, 침입량이 최대가 되는 시점에서의 변위 응답을 이용하여 등가정하중을 계산한다. 선형정적최적설계에서 계산한 등가정하중을 외력으로 적용하여 최적화를 수행하고 설계변수를 갱신한다. 이러한 설계 주기를 반복하면서 각 주기마다 목적함수의 변화량이 3 %미만이면 종료하도록 수렴조건을 정의했다.
4.2 구조최적설계 결과
제시된 문제의 최적설계 과정 및 결과에 대한 데이터를 Table 1에 정리하였다. Table 1에서 Design cycle 0은 초기 설계를 나타낸다. 초기에 목적함수인 질량은 0.05851 ton으로 계산되었다. Fig. 7의 그래프는 시간에 따른 침입량의 변화를 나타낸다. 위의 그래프가 초기 설계에서의 침입량의 변화를 나타낸 것이다. 최대침입량이 발생할 때의 시간은 대략 0.05초이며, 최대침입량의 크기는 33.98 mm이다. 초기 설계는 제한조건이 위배되지 않은 상태이지만 과만족하고 있으므로 전체적으로 과설계 상태이다.
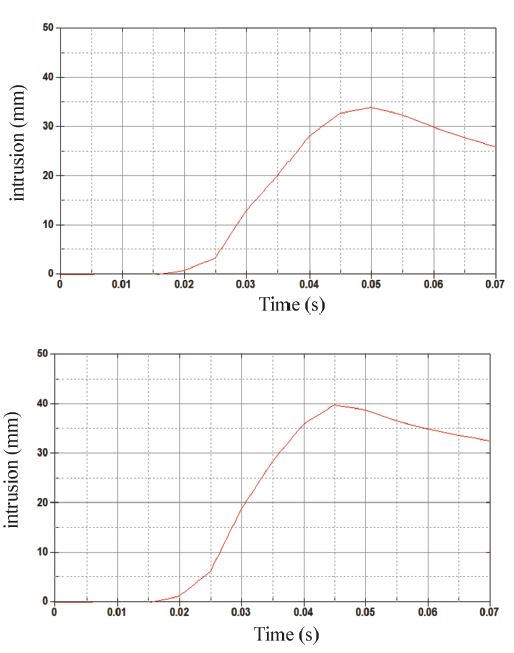
Intrusion diagram of nonlinear dynamic analysis at the initial design(above) and the optimum design(below)
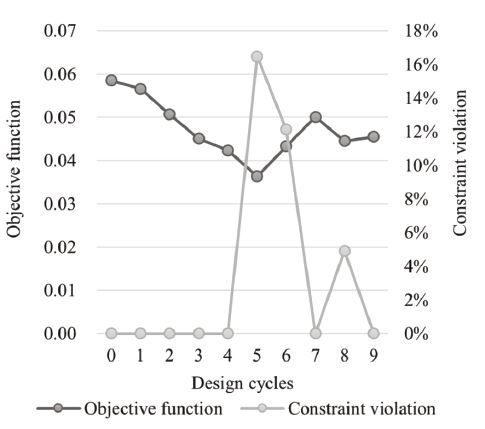
설계 주기가 진행되면서 설계변수, 목적함수, 제한조건 및 수렴조건의 변화가 Table 1에 정리되어 있다. 또한 설계 주기에 따른 목적함수 및 제한조건의 변화량을 그래프로 나타내면 Fig. 8과 같다. Table 1에서 살펴보면 9번째 설계 주기에서 목적함수의 변화량이 2.31 %가 되므로 수렴조건이 만족된다. 제한조건도 만족하므로 설계는 9번째 설계 주기에 종료되었다.
그러나 Table 1과 Fig. 8을 보면 제한조건을 만족하면서 목적함수가 가장 우수한 것은 4번째이다. 그러므로 최적해는 4번째 주기에서 얻어졌다. 목적함수는 0.04234 ton으로 초기 설계에 비해 27.6 %가 감소됐다. Fig. 7의 아래쪽 그래프가 최적해에서 침입량의 변화량이다. 0.045초에서 최대침입량이 39.88 mm으로 발생하며 제한조건을 만족시킨다. 각 설계 주기마다 비선형동적해석이 한 번씩 수행되므로 총 10번의 비선형 해석이 수행되었다.
5. 결 론
실제 자동차 충돌 사고 상황에 대응하는 전기자동차의 구조최적설계 방법이 연구되었다. 기둥측면충돌시험에 대하여 전기차의 차체와 배터리 팩을 통합하고 배터리 안전성능을 고려한 설계 방법을 제안했다. 제시된 방법은 실제 자동차충돌문제와 동일한 거대 규모의 최적설계문제에 적용되었다. 전기차의 차체와 배터리 팩의 유한요소모형을 제작하고 방법을 적용하여 결과를 도출했다. 등가정하중법을 활용해 비선형동적응답의 구조최적설계를 수행했고 적은 횟수의 동적해석만으로 우수한 해를 얻었다. 비선형동적응답을 직접 최적화 과정에서 고려하여 동적응답의 제한조건에 대해서도 잘 만족시켰다.
컴퓨터를 활용한 시뮬레이션에서 물리적 충격에 대해 배터리의 화재나 폭발 여부를 수치적으로 예측할 수 있는 방법이 없었으나, 침입량을 제한조건으로 정의하는 방법을 새롭게 제시하였고 적절한 최적화 결과를 얻었다. 논문에서는 침입량을 엄격하게 제한함으로써 사고에서 배터리 화재 등의 위험성을 최대한 줄일 수 있는 설계안에 대한 가능성을 보여주었다. 향후 설계자 판단 여부에 따라서는 침입량의 제한을 적절히 조절할 수 있을 것이다.
또한, 두께변수만이 아니라 실제로는 형상의 변화도 중요하기 때문에 형상변수를 추가하여 치수 및 형상최적설계를 동시에 수행할 수도 있을 것이다. 예제의 최적설계 결과에서 하한값으로 이동하는 설계변수도 있었는데 외력 및 제한조건이 다양하지 않았기 때문으로 보인다. 실제 자동차 설계에서는 차체의 고유진동수 등 여러 가지 설계 조건과, 다양한 하중을 동시에 고려하므로 더 의미 있는 결과가 나타날 것이다. 연구에서는 연속공간에서 설계를 수행하였으나 산업현장에서 철판의 두께 등이 이산변수로 다뤄지는 경우가 많으므로 경우에 맞도록 선형정적최적화 단계에서 이산최적설계 알고리즘을 적용하는 등의 활용 방법들도 고려해야 된다. 추가로, 침입량 외에도 배터리에 가해지는 충격력 등을 직접 고려할 수도 있겠으나, 변위제한조건만을 잘 다룰 수 있는 일반적인 등가정하중법7)이 아닌 다른 추가적인 방법이나 연구가 필요할 것이다.
한편, 전기차의 배터리 팩을 차량의 하면부에 장착하는 방식은 암묵적으로 정형화된 지 오래다. 본문에서 서술한 것과 같이 이러한 형태의 전기차들은 측면충돌사고에 대해 취약해지는 약점이 있다. 이를 해결하기 위해 사이드실 등의 강도 확보가 필수적이지만 주로 현재까지는 보강재를 추가하는 등의 임시방편으로 대처해왔다. 이것은 전기차가 갖고 있는 구조적인 설계의 문제점을 분명하게 보여준다고 할 수 있다.
연구에서는 사이드실 뿐만 아니라 배터리 팩에 사용되는 여러 부재의 설계변수를 동시에 최적화했다. 자동차사고 상황을 직접 고려하면서 전기차의 특성에 따른 안전성 향상을 위한 직관적인 설계 방법을 제시했고 방법의 효용성을 입증했다. 기존 전기차가 갖는 설계적인 문제점을 정면으로 해결 가능하다는 것을 보였기에 의미가 있다.
Acknowledgments
이 연구는 2021년도 정부(산업통상자원부)의 재원으로 한국산업기술진흥원의 지원을 받아 수행된 연구임(P0012769, 2021년 산업혁신인재성장지원사업).
References
- Regulation on Vehicle Safety Assessment Test, etc., Chapter 2, Article 2, Ministry of Land, Infrastructure and Transport Notice No.2020-307, Partially Amended, 2020.3.30.
-
J. Fang, G. Sun, N. Qiu, N. H. Kim and Q. Li, “On Design Optimization for Structural Crashworthiness and Its State of the Art,” Structural and Multidisciplinary Optimization, Vol.55, No.3, pp.1091-1119, 2017.
[https://doi.org/10.1007/s00158-016-1579-y]

- Y. H. Han, “A Study on Body Structure Optimization Considering Several Crash Load Cases,” KSAE Workshop, p.12, 2018.
-
J. S. Arora, Optimization of Structural and Mechanical Systems, World Scientific, New Jersey, 2007.
[https://doi.org/10.1142/6214]

-
H. Kurtaran, A. Eskandarian, D. Marzougui and N. E. Bedewi, “Crashworthiness Design Optimization Using Successive Response Surface Approximations,” Computational Mechanics, Vol.29, Nos.4-5, pp.409-421, 2002.
[https://doi.org/10.1007/s00466-002-0351-x]

-
B. S. Kang, G. J. Park and J. S. Arora, “A Review of Optimization of Structures Subjected to Transient Loads,” Structural and Multidisciplinary Optimization, Vol.31, No.2, pp.81-95, 2006.
[https://doi.org/10.1007/s00158-005-0575-4]

-
Y. I. Kim and G. J. Park, “Nonlinear Dynamic Response Structural Optimization Using Equivalent Static Loads,” Computer Methods in Applied Mechanics and Engineering, Vol.199, No.9-12, pp.660-676, 2010.
[https://doi.org/10.1016/j.cma.2009.10.014]

-
M. Stolpe, “On the Equivalent Static Loads Approach for Dynamic Response Structural Optimization,” Structural and Multidisciplinary Optimization, Vol.50, No.6, pp.921-926, 2014.
[https://doi.org/10.1007/s00158-014-1101-3]

-
G. J. Park and Y. M. Lee, “Discussion on the Optimality Condition of the Equivalent Static Loads Method for Linear Dynamic Response Structural Optimization,” Structural and Multidisciplinary Optimization, Vol.59, No.1, pp.311-316, 2019.
[https://doi.org/10.1007/s00158-018-2059-3]

- Y. W. Son and G. S. Huh, “Technology Development Trend of Domestic and Foreign Electric Vehicle and Technology Development Strategy of Domestic Electric Vehicle Core Parts,” The Transactions of the Korean Institute of Power Electronics, Vol.22, No.5, pp.373-381, 2017.
- J. Y. Bae and Y. Kim, “The Core Technical Trends of TESLA EV(Electric Vehicle) Motors,” The Transactions of the Korean Institute of Power Electronics, Vol.22, No.5, pp.414-422, 2017.
- Korean Agency for Technology and Standards, Korean Network On World TBT, https://www.knowtbt.kr/chinaTbt/detail/latest-china-tbt--3004210.do?nttId=3916, , 2020.
- RJS, China National Standards, http://www.gbstandards.org/GB_standard_english.asp?code=GB/T%2031467.3-2015, , 2020.
-
F. Hao, X. Lu, Y. Qiao and X. Chen, “Crashworthiness Analysis of Electric Vehicle with Energy-absorbing Battery Modules,” Journal of Engineering Materials and Technology, Vol.139, No.2, 2017.
[https://doi.org/10.1115/1.4035498]

-
M. Mudassir, F. Tarlochan and M. A. Mansour, “Nature-Inspired Cellular Structure Design for Electric Vehicle Battery Compartment: Application to Crashworthiness,” Applied Sciences, Vol.10, No.13, p.4532, 2020.
[https://doi.org/10.3390/app10134532]

-
J. I. Lee and K. C. Ha, “A Study on the Fire Risk and the Fire Investigation of Hybrid Cars,” Transactions of KSAE, Vol.27, No.2, pp.117-123, 2019.
[https://doi.org/10.7467/KSAE.2019.27.2.117]

-
S. B. Sim, C. H. Lee and S. K. Kim, “Study on the Explosion and Fire Risks of Lithium Batteries Due to High Temperature and Short Circuit Current,” Fire Science and Engineering, Vol.30, No.2, pp.114-122, 2016.
[https://doi.org/10.7731/KIFSE.2016.30.2.114]

- E. Y. Oh, D. S. Min, J. Y. Han, S. H. Jung and T. S. Kang, “Consequence Analysis of Toxic Gases Generated by Fire of Lithium Ion Batteries in Electric Vehicles,” Journal of the Korean Institute of Gas, Vol.23, No.1, pp.54-61, 2019.
-
W. Wang, F. Gao, Y. Cheng and C. Lin, “Multidisciplinary Design Optimization for Front Structure of an Electric Car Body-in-white Based on Improved Collaborative Optimization Method,” Int. J. Automotive Technology, Vol.18, No.6, pp.1007-1015, 2017.
[https://doi.org/10.1007/s12239-017-0098-1]

-
P. G. Anselma, C. B. Niutta, L. Mainini and G. Belingardi, “Multidisciplinary Design Optimization for Hybrid Electric Vehicles: Component Sizing and Multi-fidelity Frontal Crashworthiness,” Structural and Multidisciplinary Optimization, Vol.62, No.4, pp.2149-2166, 2020.
[https://doi.org/10.1007/s00158-020-02603-6]

-
J. A. Jang, H. M. Lee and H. W. Park, “A Study on the Reduction Effect of Accident Regarding the Crash Safety of KNCAP,” Transactions of KSAE, Vol.27, No.8, pp.585-594, 2019.
[https://doi.org/10.7467/KSAE.2019.27.8.585]

- Hyundai Motor Group, HMG Journal, https://news.hmgjournal.com/Tech/?p=162579, , 2020.
-
G. J. Park, “Technical Overview of the Equivalent Static Loads Method for Non-linear Static Response Structural Optimization,” Structural and Multidisciplinary Optimization, Vol.43, No.3, pp.319-337, 2011.
[https://doi.org/10.1007/s00158-010-0530-x]

-
Y. M. Lee, Y. H. Han, S. O. Park and G. J. Park, “Vehicle Crash Optimization Considering a Roof Crush Test and a Side Impact Test,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, Vol.233, No.10, pp.2455-2466, 2019.
[https://doi.org/10.1177/0954407018794259]

-
J. M. Yoon, Y. M. Lee, S. O. Park, Y. H. Han and G. J. Park, “Crash Optimization Considering the Head Injury Criterion,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, Vol.233, No.11, pp.2879-2890, 2019.
[https://doi.org/10.1177/0954407018809298]

- United States Department of Transportation, National Highway Traffic Safety Administration, https://www.nhtsa.gov/crash-simulation-vehicle-models, , 2020.
- J. O. Hallquist, LS-DYNA Keyword User’s Manual. Livermore Software Technology Corporation, 970, 299-800, 2007.
- TurboSquid, https://www.turbosquid.com/3d-models/3d-tesla-s-frame-chassis-model/1074486, , 2020.
- Altair Engineering, https://www.altair.co.kr, /, 2020.