열다공성 모델을 이용한 컴팩트 열교환기 성능 예측
Copyright Ⓒ 2021 KSAE / 183-03
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
The thermal porous medium model for 30 percent offset rate for mass production was constructed in order to conduct a CFD analysis of the air-cooled air-charged intercooler, which is a type of compact heat exchanger. This CFD model has features assumed by the charged air side offset fin and cooling air side louvered fin as the porous medium model. The air-cooled air-charged intercooler pressure drop and heat transfer performance obtained from the correlations with the existing 50 percent offset rate were compared with the pressure drop and heat transfer performance obtained from the 30 percent offset rate correlation presented in this study. The correlation between Fanning f factor and Colburn j factor with 30 percent offset fins is presented. For the offset strip fins for mass production, it was found that the Fanning f factor and Colburn j factor of 30 percent offset fins presented in this study predicted the performance of the air-cooled air-charged intercooler better than the correlation of the conventional 50 percent offset rate.
Keywords:
Compact heat exchanger, Offset strip fin, Porous medium approach, Friction correlation, Dimensionless heat transfer correlation, Computational fluid dynamics키워드:
컴팩트 열교환기, 오프셋 스트립 휜, 다공성 매질 접근법, 마찰 상관식, 무차원 열전달 상관식, 전산 유체 역학1. 서 론
차량용 컴팩트 열교환기의 일종인 공기냉각식 인터쿨러는 차량 엔진으로 유입되는 고온의 과급측 공기 온도를 낮춰 실린더 내 공기 충진율을 높여 출력과 연비를 높이고 유해 물질 배출을 낮추는 역할을 한다. 일반적으로 인터쿨러는 과급측 공기 냉각 방식에 따라 공기 냉각식 인터쿨러와 수냉식 인터쿨러로 나뉜다. 공기 냉각식 인터쿨러는 과급측과 냉각측에 각각 별도의 휜을 사용한다. 대부분의 경우 과급측에는 오프셋 스트립 휜을 사용하고, 냉각측에는 루우버 휜을 사용한다. 오프셋 스트립 및 루우버 휜 모두 유체가 이들 휜을 통과할 때, 유체 경계층 성장을 막고 전단층의 천이에 따른 난류 유동 효과를 강화시키므로, 오프셋 스트립 및 루우버 휜은 높은 열전달 효율을 갖는다. 그러므로 오프셋 스트립 휜 및 루우버 휜의 성능을 예측하기 위한 많은 연구들이 진행되어 왔다. 오프셋 스트립 휜의 경우 공기에 대하여 Joshi와 Webb1)은 천이영역을 제외한 층류 및 난류 유동 각각에 대한 Fanning f 및 Colburn j factor 상관식들을 제시했으며, Manglik와 Bergles2)는 전 레이놀즈 영역에 대하여 상관식들을 제시하였다. 그리고 높은 Prandtl 수에 대한 상관식 즉, 액체에 대한 상관식들이 Tinaut 등3) 및 김민수 등4)에서 제시되었다. 한편 루우버 휜에 대하여, 대표적인 연구는 Chang과 Wang,5-7) Achaichia와 Cowell,8) Davenport,9) Webb과 Jung,10) Sundel과 Svantesson11) 등이 있다. 그럼에도 불구하고, 오프셋 스트립 휜과 루우버 휜을 가지는 공기냉각식 인터쿨러를 3차원 시뮬레이션을 위해 격자계를 구성할 때, 전통적인 모델링 방법으로는 수십억 격자가 필요하기 때문에, 이 격자 모델을 구성하기 위해서는 오프셋 스트립 휜과 루우버 휜을 열다공성 모델로 가정해야 한다. 최근에 김택근 등12) 및 김택근13)은 루우버 휜과 오프셋 스트립 휜을 열다공성 모델로 가정하여 상관식을 제시하였으며, 루우버 휜 및 오프셋 스트립 휜에 관한 고유 투과율과 Ergun 상수를 제시하였다. 그리고 김택근 등14)은 루우버 휜을 다공성 모델로 가정한 루우버 휜을 사용하는 차량용 라디에이터에 대한 3차원 시뮬레이션 결과를 실제 시험 결과와 비교하여, 수치 해석 결과가 시험 결과에 비해 공기측 압력 강하량은 10 % 이내, 방열량은 9.5 % 이내의 정확도를 가짐을 알 수 있었다. 그리고 오프셋 스트립 휜과 루우버 휜을 사용하는 공기 냉각식 인터쿨러에 대한 압력 강하량과 성능 예측을 제시한 몇몇 연구들이 있다.15,16) 그러나 지금까지 제시된 연구들은 모두 오프셋 스트립 휜의 경우 50 % 오프셋 율을 가진다. 다양한 오프셋 율에 대하여 Goodness factor(j/f, j/f1/3, jf)는 50 % 오프셋 율에서 가장 우수함을 알 수 있었다. 하지만 차량용 열교환기의 실제 제품으로 양산되는 오프셋 스트립 휜 인 경우, 양산 과정에서 비용과 기술적인 난이도 때문에, 50 % 오프셋 율을 가지는 오프셋 스트립 휜을 생산하는 경우는 매우 한정적이다. 오히려 30 % 오프셋 율 이내의 오프셋 스트립 휜 인 경우가 대부분이다. 그러므로 3차원 수치해석을 위해, 오프셋 스트립 휜을 열다공성 모델로 가정하는 경우에도 보다 정확한 압력강하량 및 열전달 성능을 예측하기 위해 30 % 오프셋 율을 가지는 오프셋 휜에 관한 Fanning friction f 및 Colburn j factor를 제시할 필요가 있다. 그러므로 본 연구의 목적은 양산 모델에 가까운 오프셋 율을 가지는 오프셋 스트립 휜에 관한 상관식을 제시하고 이것을 이용하여 공기 냉각식 인터쿨러의 3차원 수치해석을 실시하고 시험 결과와 비교하여 50 % 오프셋 율을 가지는 오프셋 스트립 휜에 대한 상관식을 이용하는 경우에 비해 정확도가 얼마나 개선되었는지 검토하는 것이다.
2. 해석 모델 및 지배 방정식
2.1 오프셋 휜 모델
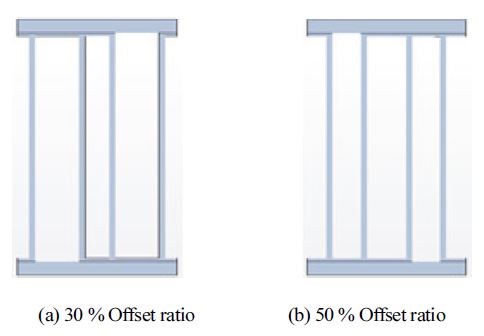
본 연구에서는 실제 양산 상황을 고려하여, 30 % 오프셋 율을 가지는 오프셋 스트립 휜에 관한 상관식들을 얻고자 한다. 이를 위해, 30 % 및 50 % 오프셋 율을 가지는 두 가지 오프셋 스트립 휜에 관한 모델들의 시뮬레이션을 수행하였으며, 특히 50 % 오프셋 율을 가지는 오프셋 스트립 휜인 경우는 기존 연구와 비교하였다. Fig. 1은 본 연구에서 다룬 30 % 및 50 % 오프셋 율을 가진 오프셋 스트립 휜 정면 형상이다. 이 두 휜은 오프셋 율만 다를 뿐 나머지 형상 정보는 동일하다.
이 두 오프셋 스트립 휜에 관한 3차원 수치해석을 위해 적용된 지배 방정식은 RANS(Reynolds Averaged Navier-Stokes Equation)이며, 난류 모델은 k-ε 모델을 사용하였다.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
여기서,
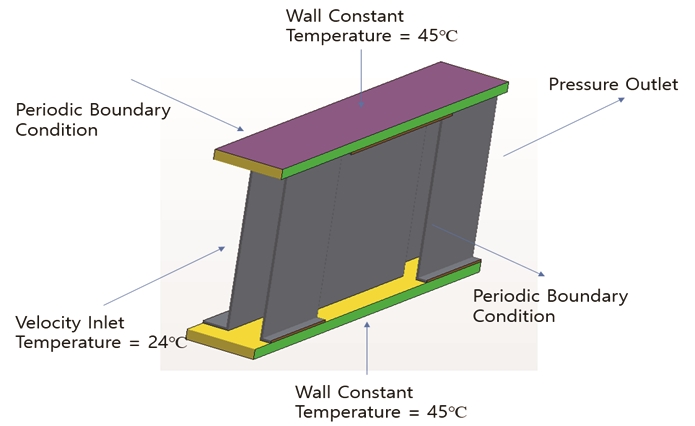
그리고 본 연구에서 다루는 오프셋 스트립 휜 CFD 모델에 관한 경계 조건은 Fig. 3과 같다. 본 연구에서 사용된 CFD 코드는 Simens사의 STAR-CCM+ 코드를 사용하였다.
2.2 다공성 모델
이와 같이 휜 모델에 대한 CFD 해석을 실시한 후, 오프셋 스트립 및 루우버 휜이 포함된 컴팩트 열교환기의 압력강하 및 방열 성능을 예측하기 위해, 본 연구에서는 휜을 다공성 매질로 가정하였다. 다공성 매질 내 압력 강하에 대한 가장 기본적인 방정식은 아래와 같이 Darcy 방정식이다.
| (8) |
여기서 K는 다공성 매질의 투과율이고, uD는 다르시안 속도이다. 이 방정식은 다공성 매질 내 유체의 평균 속도와 압력 강하에 대한 유용한 관계식이다. 그러나 이 방정식은 레이놀즈 수가 매우 낮은(Re << 1) 경우에만 적용 가능하다. 즉, 현실적인 공학 문제를 다루기에는 용도가 매우 한정적이다. 이 문제를 해결하기 위해, 제시된 방정식이 아래와 같은 Modified Darcy 방정식이다. 이 방정식은 다공성 매질 내 압력 구배에 대하여 속도 비례항(Darcy 항)과 속도 제곱 비례항(Fochhimer 항)의 합으로 구성함으로써, 점성 영역뿐만 아니라 관성 영역까지 다공성 매질 내 유동을 다룰 수 있다.
| (9) |
다공성 매질 내 에너지 방정식과 관련하여, 열적 비평형 가정을 취했으며, 이 경우 지배 방정식은 유체 및 고체 측에 대하여 다음과 같은 4차 텐서 방정식을 얻을 수 있다.
| (10) |
| (11) |
그러나 현실적으로 위의 방정식을 직접 풀거나 또는 수치해석 하는 것은 매우 어렵기 때문에, 반-경험적(Semi-empirical) 에너지 방정식을 사용하였다. 이 방정식에 대한 유체 및 고체 측에 대한 지배 방정식은 아래와 같다.
| (12) |
| (13) |
위의 반-경험적(Semi-empirical) 지배 방정식을 연속-고체 모델 (Continuous-Solid model)이라 한다. 따라서 본 연구에서 사용한 다공성 매질 내 지배 방정식은 아래와 같다.
| (14) |
| (15) |
| (16-a) |
| (16-b) |
3. 결 과
3.1 검증 및 상관식 제안
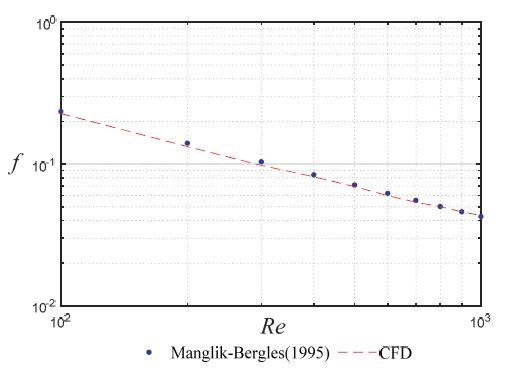
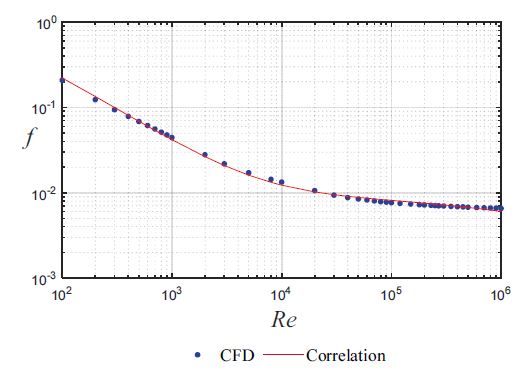
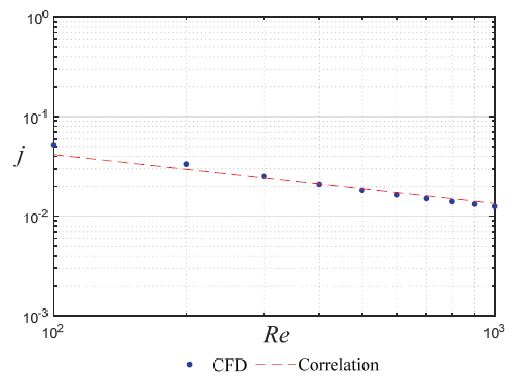
오프셋 휜의 해석 검증을 위해 본 연구에서는 50 % 오프셋 율을 가지는 오프셋 스트립 휜에 관한 수치해석과 Manglik와 Bergles2) 상관식을 비교하였다. 아래 Fig. 4와 Fig. 5는 레이놀즈 수 100부터 1,000까지 범위에서 Fanning f 및 Colburn j factor를 비교하였다.
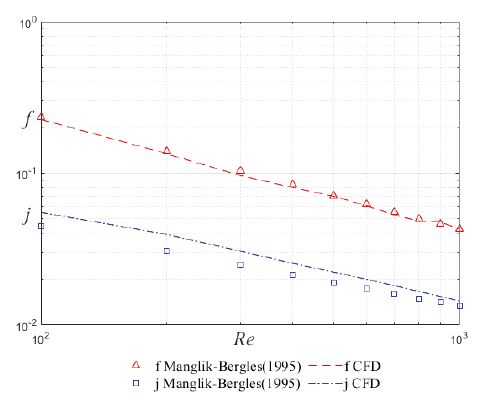
Comparison of Fanning f and Colburn j factors between Manglik-Bergles and Present CFD (50 % Offset ratio)
Fanning f factor에 대하여 본 연구의 검증용 수치 해석 결과가 Manglik and Bergles 상관식에 3 % 이내 해석 정확도를 보이는 반면, Colburn j factor에 대해서는 5 % 이내의 해석 정확도를 가짐을 알 수 있었다. 따라서 해석 기법 및 결과는 비교적 정확함을 알 수 있다. 본 연구를 위해 진행된 CFD 결과에 대한 해석 정확도를 검증하였으므로, 실제 제품에 사용되는 30 % 오프셋 율을 가지는 오프셋 스트립 휜의 대한 해석을 수행하였다.
따라서 본 연구에서는 양산 과정을 고려한 30 % 오프셋 율을 가지는 오프셋 스트립 휜에 관한 Fanning f 및 Colburn j factor를 아래 식과 같이 제시할 수 있다.
| (17) |
여기서,
3.2 3차원 수치 해석
본 연구에서 얻은 30 % 오프셋 율에 대한 Fanning f 및 Colburn j factor를 이용하여 공기 냉각식 인터쿨러에 대한 시뮬레이션을 실시했다. 이 연구에서 사용된 공기 냉각식 인터쿨러 모델은 Fig. 8과 같다.
공기 냉각식 인터쿨러 모델은 냉각측과 과급측 모두 휜이 사용되며, 냉각측은 루우버 휜 그리고 과급측으로는 오프셋 스트립 휜이 사용되었다. 그리고 시뮬레이션을 위해 냉각측 및 과급측 휜은 모두 다공성 매질로 가정하였다. 냉각측 루우버 휜에 관한 다공성 모델은 김택근 등12)의 모델을 사용하였다. 그리고 과급측에 대해서는 본 연구의 30 % 오프셋 율을 가지는 오프셋 스트립 휜에 관한 다공성 모델을 사용했다. 루우버 및 오프셋 스트립 휜에 관한 형상 정보는 Table 1과 같다.
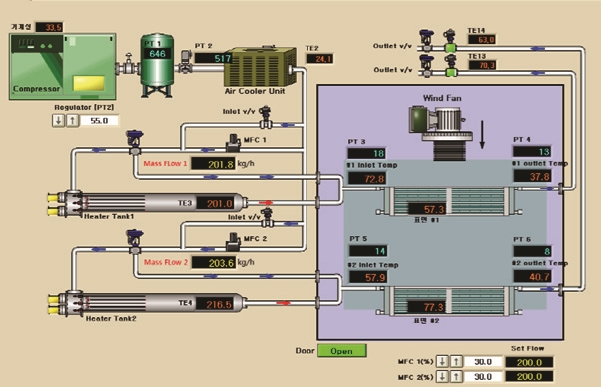
그리고 본 연구의 검증을 위해 사용된 시험기의 개략도는 Fig. 9와 같다. 이 시험기의 성능은 Table 2와 같다.
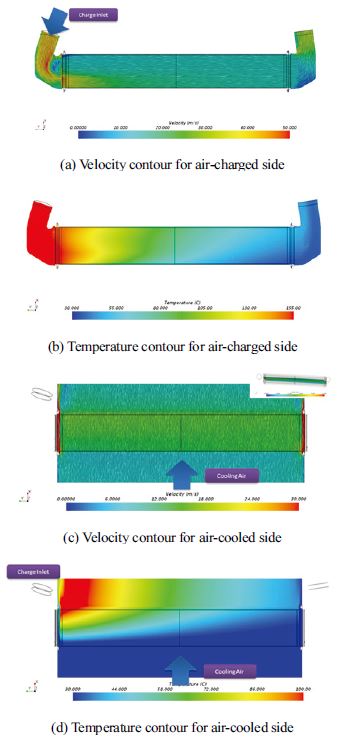
본 연구에서는 시뮬레이션을 실시하여 Fig. 10과 같은 속도 및 온도 분포를 얻을 수 있었다. Fig. 10 (a), (b)는 과급측 내부 속도 분포 및 온도 분포이며, Fig. 10 (c), (d)는 냉각측 속도 분포 및 온도 분포이다.
과급측 속도 분포는 입구 탱크 쪽에서 불균일이 관찰되는 반면에, 냉각 공기측 속도 분포는 비교적 균일함을 알 수 있다. 그러나 과급 및 냉각측 온도 분포에 대하여 입구측의 높은 온도 구배의 영향으로 입구 부근에서 큰 열전달이 일어남을 알 수 있다. 본 연구에서는 30 % 및 50 % 오프셋 율을 가지는 공기 냉각식 인터쿨러 성능 예측과 30 % 오프셋 율을 가지는 공기 냉각식 인터쿨러 제품의 시험 결과를 비교해 보았다. 비교 결과는 Table 3과 같다.

Comparison of simulation and test results for heat performance and cooling-, charge side pressure drop
30 % 오프셋 율을 가지는 제품과 동일한 모델의 공기 냉각식 인터쿨러 시뮬레이션 결과에 대하여 과급측 출구 온도는 Effectiveness 기준 5 % 이내 냉각측 출구 온도는 Effectiveness 기준 2 % 이내 과급측 압력 강하량은 5 % 이내 그리고 냉각 공기측 압력 강하량은 8 % 이내 예측 정확도를 가짐을 알 수 있다. 그러나 50 % 오프셋 율을 가지는 오프셋 스트립 휜 모델을 적용하여 얻은 시뮬레이션 결과는 냉각 공기측 압력 강하량, 과급측 및 냉각측 출구 온도에 대한 예측 정확도가 앞선 해석과 거의 동일한 수준을 보여 주는 반면에, 과급측 압력 강하량에 대해서는 28 % 수준의 큰 오차를 가짐을 알 수 있었다.
4. 결 론
지금까지 많은 연구들은 오프셋 율 50 %를 갖는 오프셋 스트립 휜에 관한 Fanning f 및 Colburn j factor 연구에 집중해 왔다. 그러나 대량 생산 체제의 산업 현장에서는 제조 비용과 기술적인 어려움 등으로 오프셋 율 30 %의 오프셋 스트립 휜을 이용하여 열교환기류를 개발 및 생산해 왔다. 그로 인해, 50 % 오프셋 율의 오프셋 스트립 휜의 성능과 실제 사용하는 오프셋 휜의 성능 차이에 의해 설계 및 제품 개발에 어려움이 있었다. 따라서 본 연구에서는 실제 제품에 사용되는 30 % 오프셋 율의 오프셋 스트립 휜의 Fanning f 및 Colburn j factor를 새롭게 제시하였으며, 이 결과를 바탕으로 과급측 및 냉각측에 각각 오프셋 스트립 및 루우버 휜을 사용하는 공기 냉각식 인터쿨러에 대한 CFD 시뮬레이션을 실시하였다. 그리고 그 해석 결과를 시험 결과와 비교하여 본 연구에서 제시한 30 % 오프셋 율을 가지는 모델을 적용한 결과가 기존의 50 % 오프셋 율을 가지는 모델을 적용한 결과 보다 높은 예측 정확도를 가짐을 알 수 있었다.
Nomenclature
| A : | area, mm2 |
| CE : | ergun constant |
| C1, C2 : | coefficients of friction factor correlation |
| cp : | specific heat of air, J/kg⋅K |
| E : | total energy (m2/s2) |
| FPDM : | fin per decimeter, cm-1 |
| f : | fanning friction factor |
| hsf : | interfacial heat transfer coefficient, W/m2⋅K |
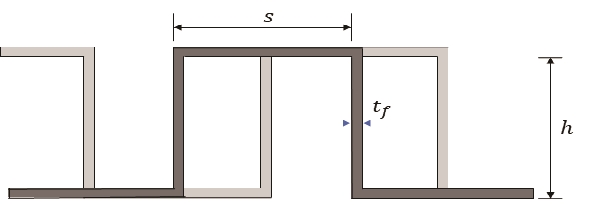
| h : | height of the fin, mm |
| j : | colburn j factor |
| K : | permeability, m2 |
| k : | turbulent kinetic energy |
| l : | fin length, mm |
| p : | pressure, Pa |
| Re : | reynolds number |
| Sij : | strain rate, m-1 |
| s : | spacing between adjacent fin, mm |
| T : | temperature, °C |
| Tf : | temperature of fluid in porous medium, °C |
| Ts : | temperature of solid in porous medium, °C |
| tf : | fin thickness, mm |
| u : | velocity, m/s |
| α : | correction factor |
| ɣ : | porosity |
| ε : | turbulent dissipation rate, m2/s2 |
| μ : | viscosity, Pa⋅s |
| ν : | kinematic viscosity, m2/s |
| νt : | eddy viscosity, m2/s |
| ρ : | density, kg/m3 |
Subscripts
| c : | cross sectional direction |
| D : | darcian entity |
| fs : | fluid-solid interface |
| i : | i directional vector |
| j : | j directional vector |
| sf : | solid-fluid interface |
Acknowledgments
이 논문은 2019학년도 한국기술교육대학교 교수 교육연구진흥과제 지원에 의하여 연구되었습니다.
References
-
H. Joshi and R. Webb, “Heat Transfer and Friction in Offset Strip Fin Heat Exchanger,” International Journal of Heat and Mass Transfer, Vol.30, No.1, pp.69-80, 1987.
[https://doi.org/10.1016/0017-9310(87)90061-5]

-
R. Manglik and A. Bergles, “Heat Transfer and Pressure Drop Correlations for the Rectangular Offset Strip Fins Compact Heat Exchanger,” Experimental Thermal Fluid Science, Vol.10 pp.171-180, 1995.
[https://doi.org/10.1016/0894-1777(94)00096-Q]

-
F. Tinaut, A. Melgar and R. Ali, “Correlations for Heat Transfer and Flow Friction Characteristics of Compact Plate-type Heat Exchangers,” International Journal of Heat and Mass Transfer, Vol.35, No.7, pp.1659-1665, 1992.
[https://doi.org/10.1016/0017-9310(92)90136-G]

-
M. Kim, S. Lee, S. Yook and K. Lee, “Correlations and Optimization of a Heat Exchanger with Offset-strip Fins,” International Journal of Heat and Mass Transfer, Vol.54, pp.2073-2079, 2011.
[https://doi.org/10.1016/j.ijheatmasstransfer.2010.11.056]

-
Y. Chang and C. Wang, “A Generalized Heat Transfer Correlation for Louver Fin Geometry,” International Journal of Heat and Mass Transfer, Vol.40, No.3, pp.533-544, 1997.
[https://doi.org/10.1016/0017-9310(96)00116-0]

-
Y. Chang and C. Wang, “Air Side Performance of Brazed Aluminum Heat Exchangers,” Journal of Enhanced Heat Transfer, Vol.3, No.1, pp.15-28, 1996.
[https://doi.org/10.1615/JEnhHeatTransf.v3.i1.20]

-
Y. Chang, K. Hsu, Y. Lin and C. Wang, “A Generalized Friction Correlation for Louver Fin Geometry,” International Journal of Heat and Mass Transfer, Vol.43, pp.2237-2243, 1999.
[https://doi.org/10.1016/S0017-9310(99)00289-6]

-
A. Achaichia and T. Cowell, “Heat Transfer and Pressure Drop Characteristics of Flat Tube and Louvered Plated Fin Surfaces,” Experimental Thermal and Fluid Science, Vol.1, No.2, pp.147-157, 1998.
[https://doi.org/10.1016/0894-1777(88)90032-5]

- C. Davenport, “Correlation for Heat Transfer and Flow Friction Characteristics of Louvered Fin,” AIChE Symposium Series, Vol.79, No.3, pp.19-27, 1983.
- R. Webb and S. Jung, “Air-Side Performance of Enhanced Brazed Aluminium Heat Exchangers,” Conference Proceedings by ASHRAE, Vol.98 Pt2, pp.391-401, 1992.
- B. Sunden and J. Svantesson, “Correlation of j- and f-factors for Multilouvered Heat Transfer Surfaces,” Proceedings of the 3rd UK National Heat Transfer Conference, pp.805-811, 1992.
-
T. Kim, H. Kang and J. Lee, “A Porosity Model for Flow Resistance Calculation of Heat Exchanger with Louvered Fins,” Journal of Mechanical Science and Technology, Vol.30, No.4, pp.1943-1948, 2016.
[https://doi.org/10.1007/s12206-016-0353-9]

-
T. Kim, “Development of Friction Model for Offset Strip Fin with Separated Viscous and Inertial Resistances,” Journal of Mechanical Science and Technology, Vol.31, No.12, pp.6051-6057, 2017.
[https://doi.org/10.1007/s12206-017-1149-2]

-
T. Kim, S. Lee and S. Pae, “Method of Predicting Radiator Temperature Distributions for Thermal Fatigue Analysis,” Journal of Mechanical Science and Technology, Vol.31, No.10, pp.5059-5066, 2017.
[https://doi.org/10.1007/s12206-017-0954-y]

-
F. Brotz, W. Kuhnel and Y. Chen, “Virtual Temperature Cycle Testing of Automotive Heat Exchangers by Coupled Fluid Structure Simulation,” SAE International, Vol.1, pp.612-617, 2008.
[https://doi.org/10.4271/2008-01-1210]

-
F. Roger and A. Chidley, “Thermo-mechanical Fatigue Design of Automotive Heat Exchangers,” European Journal of Computational Mechanics, Vol.22, pp.228-235, 2013.
[https://doi.org/10.1080/17797179.2013.820895]