딥러닝 기반의 오토 튜닝 PID 제어를 이용한 차량 경로 제어 모델 개발
Copyright Ⓒ 2021 KSAE / 182-01
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
The path tracking of the intelligent vehicle is a complex and key technology research. In the present study, a vehicle path tracking controller was designed by a deep learning auto-tuning PID(proportion integral derivative) controller. The Kp, Ki, and Kd parameters were optimized via deep neural network model in real-time. The yaw angle of the vehicle centroid and the lateral distance between the vehicle centroid and the road lane were used as inputs to the controller. In addition, the performance of the controller was compared and verified with 2-Dof, 7-Dof, and full vehicle models. The proposed controller was operated on a double lane change road and a curved road. Results showed that the proposed path tracking controller has high real-time and robustness.
Keywords:
Vehicle path control, Deep learning, Neural network, Auto-tuning PID, Vehicle dynamics simulation키워드:
차량경로제어, 딥러닝, 신경망, 오토 튜닝 PID, 차량 동적 시뮬레이션1. 서 론
차선 유지 보조 시스템, 도로 이탈 방지 시스템, 후측방 충돌 회피 지원 시스템, 긴급 제동 시스템과 같은 다양한 첨단 운전자 지원 시스템(ADAS: Advanced driving assistance system)이 보급됨에 따라서 ADAS의 개발과 성능 검증을 위하여 차량 동역학 시뮬레이션 기법이 많이 적용되고 있다. ADAS 장착 차량의 동적 거동을 모사함에 있어서 필수적인 요소 중의 하나는 시스템에 의해서 결정된 주행 경로를 차량이 정확하게 추종할 수 있는 차량의 경로 추종 제어 모델이다.
경로 추종 제어를 위해서 고전 제어 및 현대 제어 이론에 기반한 다양한 제어 기법이 제시되었다. 고전 제어 중 PID를 많이 사용하지만 PID는 모델과 입력에 따라 계수가 달라져야 하기 때문에 계수를 변경해 주는 연구가 진행되었다. 본 연구에서는 최근 많은 관심을 받고 있는 딥러닝에 기반한 PID 오토 튜닝 차량 경로 제어 모델을 제안하고자 한다.
Ponce 등1)은 뉴럴 네트워크의 PID 오토 튜닝에 대한 이론을 제시하였다. PID 오토 튜닝이란 이전의 값들을 사용하여 자동으로 PID의 계수를 변화시켜 제어를 최적화하는 방법이다. Ponce의 논문에서 뉴럴 네트워크의 입력 값으로 사용되는 변수는 시간 지연을 통해 3개로 분할되었다. 분할된 변수들은 수식을 통해 변화된다. 뉴럴 네트워크는 3개의 변수로 이루어진 2개의 층으로 구성되어 있기 때문에 가중치는 6개가 필요하다. 하지만 6가지의 가중치를 계산하는 수식이 단순하지 않기 때문에 실시간 계산을 하기에는 어려움이 있다.
Alvarado 등2)은 뉴럴 네트워크의 오토 튜닝에 대한 식을 사용하여 3축 이동과 3축 회전이 가능한 6자유도 모델에 대하여 정의하고, 주어진 궤적을 추적하는 제어에 대하여 연구를 하였다. 이 논문에서 뉴럴 네트워크를 사용한 PID 오토 튜닝에 대한 Matlab Simulink 개념도를 제시한다. 뉴럴 네트워크의 입력 변수 4가지를 사용하였다. 입력 변수에는 조향 각, 위치추적 오차, 자동차 모델의 출력, 주어진 궤적이 들어갔으며 출력으로는 PID 계수가 출력되었다. 입력 변수는 디지털 PID 알고리즘을 사용하여 변화하였다. 뉴럴 네트워크의 구성은 Ponce의 수식을 사용하였다. 출력된 계수는 PID 제어로 들어가서 다시 차량 모델을 제어하였다.
Han 등3)은 2자유도 차량 모델을 정의하고 뉴럴 네트워크를 이용한 PID 오토 튜닝 제어를 통하여 주어진 궤적을 추적하였다. 뉴럴 네트워크의 입력 변수를 차량의 횡 방향 변위를 지연시켜서 사용하였고 총 3가지의 가중치를 PID 계수를 사용하여 차량의 횡 방향 제어를 수행하였다. 하지만 차량의 선수각은 뉴럴 네트워크를 사용하지 않고 따로 되먹임 제어를 수행하여 차량의 방향을 제어하였다.
이 논문에서는 Han 등이 사용한 PID 계수를 뉴럴 네트워크의 가중치로 사용하는 방법을 변형시켜 사용하였고 차량 모델의 선수각과 횡 방향 변위를 결합시켜 뉴럴 네트워크의 입력 값으로 사용하였다. Ponce 등이 사용한 입력 변수의 지연 방식을 채택하였지만 단순히 지연시키지 않고 디지털 PID 알고리즘을 사용하여 지연 값을 변화시켰다. Alvarado 등이 사용한 Matlab Simulink의 개념도를 참조하여 제어를 구성하였다.
설계한 제어는 주어진 궤적을 차량 모델이 횡 방향 제어를 통하여 궤적을 추종하는 제어이다. 제어의 검증을 위하여 2자유도 차량 모델을 기반으로 기존 PID와 뉴럴 네트워크 PID 오토 튜닝을 입력과 응답에 따른 각각의 시뮬레이션을 수행하였다. 입력의 종류는 횡 방향 변위와 요 속도이다. 성능 확인을 위한 시나리오는 정상상태 응답인 정상 원 선회 거동과 과도 응답인 이중 차선 변경이다. 제어 검증은 횡 방향 변위에 대한 오차, 각도에 대한 오차와 전체 궤적을 비교하였다.
일반적인 경로 제어의 경우 카메라 비전 인식을 통해 현재 도로가 아닌 몇 미터 뒤의 도로를 인식하여 사전에 조향을 제어한다. 하지만 몇 미터 뒤의 목표 궤적을 추적하는 방식은 날씨와 환경에 따라 제어 성능이 변화할 수 있다고 판단하였다. 따라서 이 논문에서는 차량의 무게 중심에서의 거리 오차와 각도 오차를 사용하여 날씨와 환경에도 제어 성능의 변화가 없는 제어를 설계하였다.
2. 차량 모델
이 논문에서 사용한 차량 모델은 2자유도, 7자유도, Full 차량 모델이 사용되었다. 2자유도 차량 모델은 Rajamani 등4)이 서술한 차량 모델을 사용하였다. 7자유도 차량 모델은 Lia 등5)이 서술한 차량 모델과 Pacejka와 Bakker6)의 Magic formula 타이어 모델을 사용하였다. Full 차량 모델은 CARMAKER의 차량 모델을 사용하였다. 또한 제어를 정의하기 위하여 2자유도 차량 모델의 수식을 활용하였다.
3. 뉴럴 네트워크 PID 오토 튜닝 경로 제어 모델
차량을 제어하기 위하여 뉴럴 네트워크를 사용한 제어 방법을 제시한다. 제어 방법은 고전적인 제어 방식인 PID를 PID의 계수를 고정하지 않고 자동으로 변경하는 오토 튜닝 방법을 사용하여 뉴럴 네트워크를 통하여 PID의 계수를 실시간으로 수정하여 차량의 경로를 추종하는 제어 방법이다. Han 등3)이 제안한 제어 방법은 도로와의 차량 무게 중심 사이의 거리를 입력 값으로 사용하는 방식이다. 하지만 도로와의 각도에 대한 정보를 뉴럴 네트워크의 입력 값으로 반영하지 않기 때문에 각도에 관련된 오차를 뉴럴 네트워크를 통하여 수정할 수 없다. 따라서 이 논문에서는 도로와 차량 간의 거리와 각도에 대한 변수들을 동시에 반영하는 제어를 제시한다. 또한 실시간 제어를 수행하기 위하여 복잡한 수식을 사용하지 않고 PID 계수를 사용하여 가중치 업데이트를 진행하였다. 제어를 정의함에 앞서 2자유도 차량 모델을 사용하여 제어의 입력 변수들을 정의하였다.
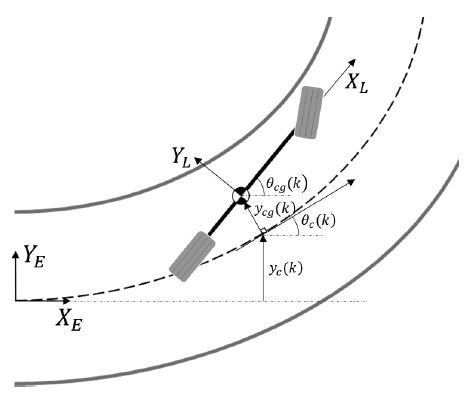
Fig. 1은 제어 개념도를 제시한다. XE-YE는 기준 좌표계이고 XL-YL는 차량 좌표계이다. 기준 좌표계의 XE축으로부터 모델의 목표 궤적인 차선 중심 거리까지의 수직 거리 yc(k), 차선의 접선부터 차량의 무게 중심까지 수직 거리 ycg(k), 차선의 접선과 기준좌표계 XE 사이의 각도 θc(k), 차량 좌표계 XL과 기준좌표계 XE 사이의 각도 θcg(k)이다. 위의 변수에서 (k)는 시간순으로 획득한 변수의 k번째 값을 의미한다. 위의 변수의 첨자에서 L은 로컬, E는 글로벌, c은 중심차선, cg는 질량 중심을 의미한다. 위의 yc(k), ycg(k), θc(k), θcg(k)는 Rajamani 등4)이 제시한 2자유도 모델의 수식들을 사용하여 값을 추출하였다. 각 변수들의 측정은 안다고 가정하였다.
식 (1)에서 거리에 대한 오차 변수 ed(k)는 위에서 설명한 yc(k)와 ycg(k)의 차를 사용하였다. 식 (2)에서 각도에 대한 오차 변수 eθ(k)는 위에서 설명한 θc(k)와 θcg(k)의 차를 사용하였다. ed(k)와 eθ(k)를 뉴럴 네트워크의 입력 변수로 사용한 제어 방법을 제시한다. Fig. 8는 제안한 제어의 개념도를 제시한다.
| (1) |
| (2) |
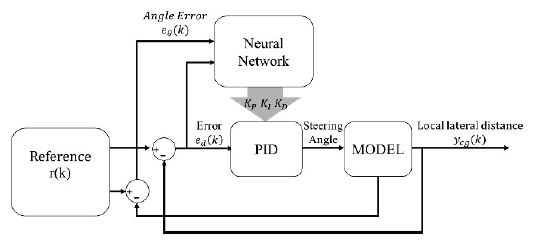
Fig. 2에서 r(k)는 기준 값으로 차선에서 차량의 무게 중심 사이의 거리 ycg(k)의 목표 값인 yc(k)와 차량의 각도 오차 θcg(k)의 목표 값인 도로의 곡률 반경 θc(k)를 포함한다. 차량 모델에서 출력된 ycg(k)는 yc(k)과 피드백되어 ed(k)로서 PID 제어의 기준 값으로 들어가며 뉴럴 네트워크의 입력 변수로서 사용된다. 또한 차량 모델에서 출력된 θcg(k)는 eθ(k)과 피드백되어 eθ(k)로서 뉴럴 네트워크의 입력 변수로서 사용된다. 거리 오차에서의 r(k)의 값은 0이고 각도 오차에서의 r(k) 값은 도로의 곡률 반경을 사용하였다.
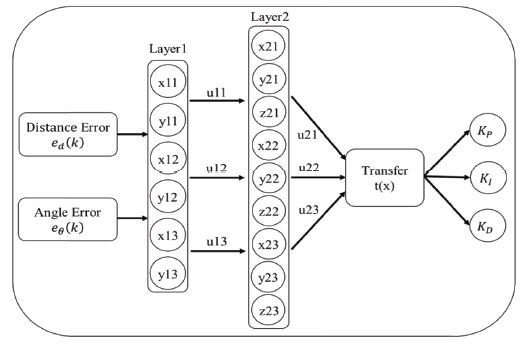
Fig. 3에서 뉴럴 네트워크는 두 개의 입력 변수를 지연을 통하여 분할시켜 구성하였다. ed(k)을 사용하여 레이어 1을 구성하는 x11(k), x12(k), x13(k)를 아래와 같이 형성한다.
| (3) |
| (4) |
| (5) |
위 식에서 ed(k-1)는 거리 오차를 1회 지연시킨 값이고 ed(k-2)는 거리 오차 오차를 2회 지연시킨 값이다. 도로와의 거리 오차 ed(k)를 분할해 3가지 변수로 만들어 내기 위하여 시간 지연을 통한 알고리즘을 사용, x11(k), x12(k), x13(k)를 형성하였다. 또한 도로와의 각도 오차 eθ(k)을 사용하여 아래와 같이 y11(k), y12(k), y13(k)을 형성한다.
| (6) |
| (7) |
| (8) |
위 식에서 eθ(k-1)는 Heading angle를 1회 지연시킨 값이고 eθ(k-2)는 Heading angle를 2회 지연시킨 값이다. 한 도로와의 각도 오차 eθ(k)를 분할해 3가지 결과 값을 가지기 위하여 y11(k), y12(k), y13(k) 를 형성하였다.
기존의 Han 등3)은 PID의 계수를 뉴럴 네트워크의 가중치에 직접적으로 사용하여 제어기를 구성하였다. 하지만 2개의 레이어에 PID의 계수를 직접적으로 사용하면 출력 값의 크기가 매우 커지기 때문에 PID의 계수를 직접적으로 사용하지 않고 시그모이드 함수를 적용하였다. 시그모이드 함수는 출력 값을 0~1로 제한하여 갑작스러운 외란에도 안정된 반응을 보여 준다. 뉴럴 네트워크의 가중치는 PID의 계수인 KP, KI, KD를 시그모이드 함수를 사용하여 w1(k), w2(k), w3(k)로 정의하였다. 앞에서 정의한 x1i(k)와 y1i(k)를 결합하여 아래와 같은 수식을 제시한다.
| (9) |
| (10) |
| (11) |
| (12) |
위 식 (12)에서 도로와 거리 오차인 ed(k)와 각도 오차인 eθ(k)로 생성한 x1i(k)와 y1i(k)를 더하고 위에서 정의한 가중치 함수 wi(k)를 곱하여 생성된 u1i(k)은 두 오차에 대한 반응을 반영한다. ui(k)는 1번 레이어의 결과 값이다. i는 1~3을 입력으로 받는다. 2번 레이어를 구성하기 위하여 위에서 사용한 시간 지연을 통한 변수 생성을 다시 수행한다.
| (13) |
| (14) |
| (15) |
위 식에서 u11(k-1)는 에러를 1회 지연시킨 값이고 u11(k-2)는 에러를 2회 지연시킨 값이다. 1번 레이어의 결과 값 중 u11(k)를 분할해 3가지 결과 값을 가지기 위하여 x21(k), x22(k), x23(k) 를 형성하였다.
| (16) |
| (17) |
| (18) |
위 식에서 u12(k-1)는 에러를 1회 지연시킨 값이고 u12(k-2)는 에러를 2회 지연시킨 값이다. 1번 레이어의 결과 값 중 u12(k)를 분할해 3가지 결과 값을 가지기 위하여 y21(k), y22(k), y23(k)를 형성하였다.
| (19) |
| (20) |
| (21) |
위 u13(k-1)식에서 는 에러를 1회 지연시킨 값이고 u13(k-2)는 에러를 2회 지연시킨 값이다. 1번 레이어의 결과 값 중 u13(k)를 분할해 3가지의 결과 값을 가지기 위하여 z21(k), z22(k), z23(k)를 형성하였다. 생성된 x2i(k), y2i(k), z2i(k)를 사용하여 2번 레이어를 구성한다.
| (22) |
위 식 (22)는 1번 레이어에서 생성된 u1i(k)를 사용하여 생성한 x2i(k), y2i(k)와 z2i(k)를 더하고 위에서 정의한 가중치 함수 wi(k)를 곱하여 생성된 u2i(k)은 2번 레이어의 결과 값으로서 PID의 계수를 의미한다. t(x)를 거쳐 나온 u21(k)은, KP, u22(k)은 KI이고 u23(k)은 KD이다. Fig. 2에서 최종적으로 사용한 전달 함수는 식 (23)과 같다.7)
| (23) |
위 식 (23)에서의 x는 u2i(k)로 이루어진 벡터이다. t(x)는 전달 함수로써 사용되며 KP, KI, KD 값을 출력한다. 또한 출력된 PID의 계수를 역전파로 이전 식 (9)~(11)로 보내 실시간으로 변동되는 값들을 반영하여 계산한다.
4. 성능 검증 결과
4.1 시뮬레이션 시나리오 정의
제어의 정상상태 반응을 확인하기 위하여 ISO 41388)을 참조하여 R=100 m의 일정한 곡률로 주행하는 궤적을 정의한다. 80 km/h의 주행 속도에서 횡 방향 가속도가 4.9 m/s2를 생성하는 R=100 m의 곡률 반경을 가지는 원을 주행하였다. 또한 제어의 과도 응답 반응을 확인하기 위하여 ISO 3888-19)을 참조하여 이중 차선 변경 궤적을 정의한다. 차량의 주행 속도는 80 km/h로 주행하였다.
4.2 제어 성능 검증
2자유도 차량 모델을 사용하여 제어기를 검증하였다. 제어의 검증을 위하여 2자유도 차량 모델을 기반으로 기존 PID와 뉴럴 네트워크 PID 오토 튜닝을 입력과 응답에 따라 4가지 시뮬레이션을 수행하였다. 입력의 종류는 횡 방향 변위와 요 속도이고 응답은 정상상태 응답인 정상 원 선회 거동과 과도 응답인 이중 차선 변경이다. 제어 검증은 횡 방향 변위에 대한 오차 값을 비교하였다. 응답에 따라 4가지 시뮬레이션을 수행하였다. 기존의 PID는 고정된 KP, KI, KD 값을 사용하며 각각 20, 10, 10을 사용하였다.
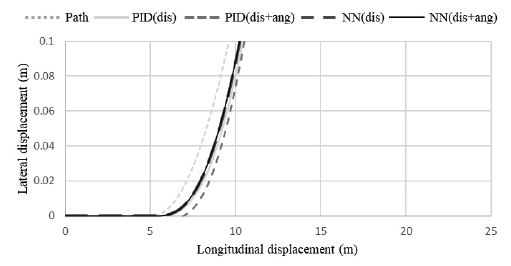
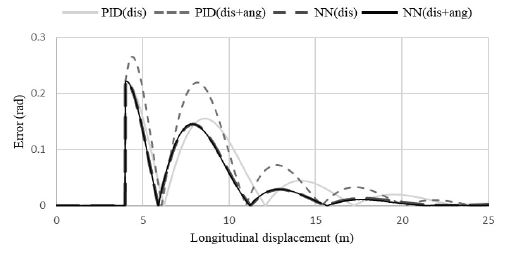
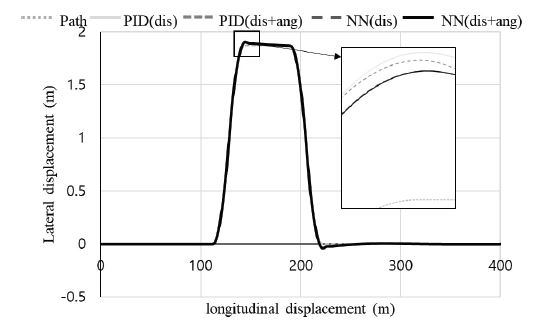
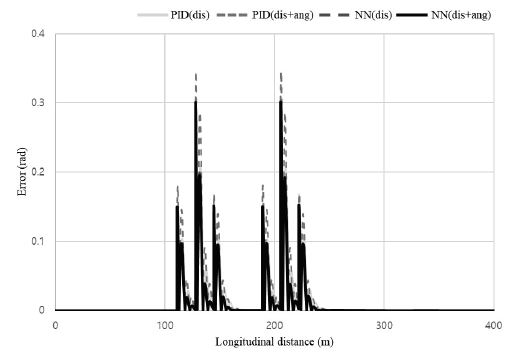
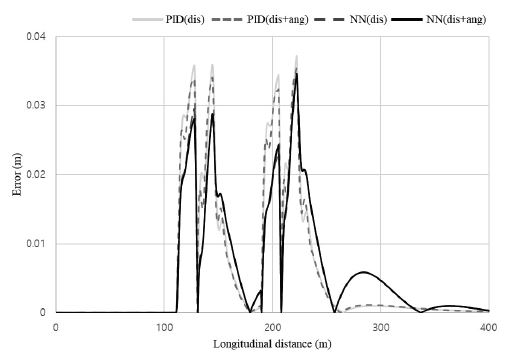
R=100 m steady circular test의 시험 결과를 아래 Figs. 4~6에 제시하였다. PID(dis)는 PID의 입력 변수를 횡 방향 변위 값만 사용하여 나타난 결과이고 PID(dis+ang)는 PID의 입력 변수를 횡 방향 변위와 요 속도를 혼합하여 사용한 결과이다. 또한 NN(dis)는 뉴럴 네트워크의 입력 변수를 횡 방향 변위 값만 사용한 결과이고 NN(dis+ang)는 뉴럴 네트워크의 입력 변수를 횡 방향 변위와 요 속도를 혼합하여 사용한 결과이다. 그림을 설명하기 위하여 사용한 dis는 Distance의 약자이고 ang는 Yaw angle의 약자이다. Fig. 4는 4가지 제어 방식들이 Steady state circular test의 궤적 추적이 가능함을 보여 준다. Fig. 5, 6에서는 직선 주행에서 곡선 주행으로 바뀌는 구간에서 오류가 발생하고 정상상태에 도달하면 오차가 발생하지 않는 것을 보여 준다. 각도 오차를 확인하기 위해 식 (24)을 사용하여 각도 오차 eθ(k)의 절댓값을 계산하였고, 그 그래프를 Fig. 5에 도시하였다.
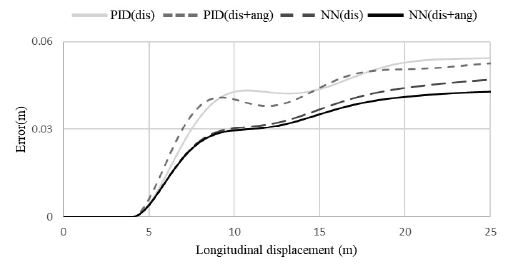
정상상태 반응의 각도 오차 결과는 PID보다 뉴럴 네트워크를 사용한 제어 반응 오차의 최대 피크 크기가 더 적었다. 뉴럴 네트워크의 입력 변수를 횡 방향 변위만 사용한 것보다 횡 방향 변위와 요 속도를 혼합하여 사용한 것이 오차가 더 적은 것을 확인하였다. Fig. 6에서 거리 오차를 계산하기 위해 식 (25)을 사용하여 거리 오차 ed(k)의 절댓값의 그래프를 제작하였다. 정상상태 반응의 결과로는 PID보다 뉴럴 네트워크를 사용한 제어의 반응 오차의 최대 피크 크기가 더 적고 빠르게 안정되었다. 뉴럴 네트워크의 입력 변수를 횡 방향 변위만 사용한 것보다 횡 방향 변위와 요 속도를 혼합하여 사용한 것이 오차가 더 적은 것을 확인하였다.
정상상태에서는 이 논문에서 제시한 각도 오차와 거리 오차를 혼합하여 사용한 제어기의 성능이 가장 뛰어났다. 거리 오차만을 사용하였던 과거의 뉴럴 네트워크 PID 오토 튜닝과는 다르게 각도 오차를 신경망 구조에 포함시켜 각도로 인해 발생한 오차를 보상해 주었기 때문이다.
| (24) |
| (25) |
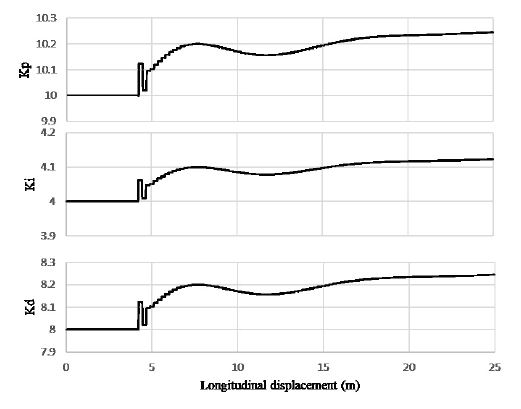
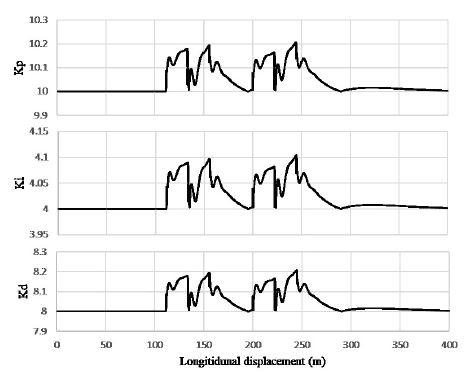
이 논문에서는 PID 계수를 실시간으로 변경하기 때문에 정상상태 반응에서의 PID 계수의 결과 값을 제시한다. Fig. 7는 정상상태 반응에서의 PID 계수의 결과 값이다. NN(dis+ang)의 기본 PID 계수는 기존의 PID과 동일한 PID 계수를 사용한다. 그 후 도로에 따라 계수가 변경된다.
KP는 10부터 시작하여 변경이 시작된 후 20 m 이후부터는 안정화된다. 약 0.24 정도 상승하는 모습을 보여 준다. KI는 4부터 시작되어 마찬가지로 20 m 이후부터 안정화된다. 약 0.11 정도 상승하는 모습을 보여 준다. KD는 8부터 시작되어 마찬가지로 20 m 이후부터 안정화된다. 약 0.23 정도 상승하는 모습을 보여 준다.
확인 결과 KP와 KD에 비하여 KI의 상승률이 적은 것을 알 수 있었다. 이러한 결과는 기본 PID 계수가 작은 것이 영향을 준 것으로 판단된다. 또한 I의 경우 커질수록 반응속도가 느려지기 때문에 주파수와 같이 지속적으로 변화하는 데이터를 활용하여 교육시킨 이 논문의 제어기의 경우 I를 적게 변화시키게 교육된 것으로 보인다.
Double lane change test의 시험 결과를 아래 Figs. 8~10에 제시하였다. Fig. 9는 4가지 제어 방식 Double lane change test의 궤적 추적이 가능한 것을 보여준다. Fig. 9에서 각도 오차를 계산하기 위해 식 (24)을 사용하여 각도 오차 eθ(k)의 절댓값의 그래프를 제작하였다.
과도 응답 반응의 각도 오차 결과는 PID보다 뉴럴 네트워크를 사용한 제어 반응 오차의 최대 피크 크기가 더 적고 빠르게 안정되었다. 뉴럴 네트워크의 입력변수를 횡 방향 변위만 사용한 것보다 횡 방향 변위와 요 속도를 혼합하여 사용한 것이 오차가 더 적은 것을 확인하였다. Fig. 9에서 거리 오차를 계산하기 위해 식 (25)을 사용하여 거리 오차 ed(k)의 절댓값의 그래프를 제작하였다. 과도 응답 반응의 결과로는 PID보다 뉴럴 네트워크를 사용한 제어의 반응의 오차의 최대 피크의 크기가 더 적었다. 뉴럴 네트워크의 입력변수를 횡 방향 변위만 사용한 것보다 횡 방향 변위와 요 속도를 혼합하여 사용한 것이 오차가 더 적은 것을 확인하였다. 하지만 안정화 속도는 뉴럴 네트워크보다 PID가 빠른 것을 확인하였다.
과도 응답에서는 이 논문에서 제시한 제어기가 가장 적은 오버 슈트를 보였지만 PID보다 안정화 속도가 느렸다. 그 이유는 뉴럴 네트워크를 다양한 변화에 반응하기 위하여 주파수 반응과 유사한 데이터로 교육시켰기 때문이다. 교육 데이터의 영향으로 변화에는 빠르게 반응하여 오버 슈트는 적지만 곡선 도로 이후 안정화 단계에서 악영향을 준 것으로 생각된다.
Fig. 11는 과도 응답에서의 PID 계수의 결과 값이다. NN(dis+ang)의 기본 PID 계수는 기존의 PID과 동일한 PID 계수를 사용한다. 그 후 도로에 따라 계수가 변경된다.
KP는 10부터 도로에 따라 변화하며 최대 약 0.2 정도 상승하는 모습을 보여 준다. KI는 4부터 도로에 따라 변화하며 최대 약 0.1 정도 상승하는 모습을 보여 준다. KD는 8부터 도로에 따라 변화하며 최대 약 0.2 정도 상승하는 모습을 보여 준다.
확인 결과 정상상태와 마찬가지로 KP와 KD에 비하여 KI의 상승률이 적은 것을 알 수 있었다. 도로의 변화가 끝나는 약 270 m 지점부터 기존의 PID 계수로 복귀하는 것을 확인할 수 있었다. 이러한 결과로부터 기본적으로는 고정된 PID 계수의 성능을 유지하면서 환경이 변경되는 경우에만 계수 변화가 작동하여 제어 성능을 향상시킨다는 것을 확인하였다. 하지만 급격한 변화에도 PID 계수의 변화가 적은 것은 PID 계수를 2개의 레이어를 통하여 받았기 때문이라고 판단된다.
4.3 2 dof, 7 dof, Full 차량 모델 제어 비교
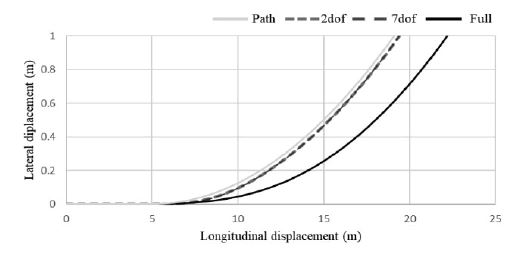
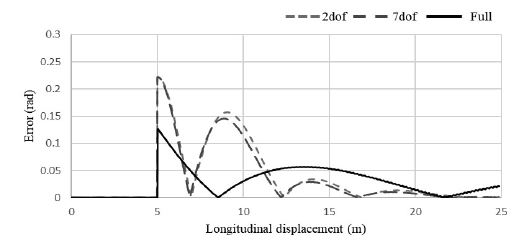
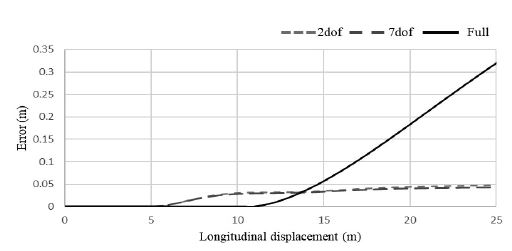
앞에서 정상상태 반응과 과도 응답의 반응의 결과가 기존의 제어 방식들보다 위에서 새롭게 제안한 제어기의 성능이 우수한 것을 확인하였기 때문에 2 dof, 7 dof, Full 차량 모델에 따른 제어 결과를 비교하였다. 2 dof, 7 dof, Full 차량 모델 R=100 m steady circular test의 시험 결과를 Fig. 12~14에 제시하였다. Fig. 12에서 R=100 m인 궤적을 모든 자유도의 모델이 제어가 가능한 것을 확인하였다. Fig. 13에서 각도 오차를 계산하기 위해 식 (24)을 각도 오차 eθ(k)의 절댓값의 그래프를 제작하였다. 정상상태 반응 시험 결과 2자유도 차량 모델과 7자유도 차량 모델의 결과는 매우 유사한 오차 값을 보였고, Full 차량 모델의 경우 다른 자유도에 비하여 안정화되는 속도가 느리고 시간이 지날수록 0으로 수렴되는 것을 확인하였다. Fig. 14에서 거리 오차를 계산하기 위해 식 (25)를 사용하여 거리 오차 ed(k)의 절댓값 그래프를 제작하였다. 정상상태 반응 시험 결과 2자유도 차량 모델과 7자유도 차량 모델의 결과는 매우 유사한 오차 값을 보였고, Full 차량 모델의 경우 다른 자유도에 비하여 초기 피크 값은 낮지만 안정화되는 속도가 느린 것을 확인하였다. Fig. 14에서 거리 오차를 계산하기 위해 식 (25)를 사용하여 거리 오차 ed(k)의 절댓값 그래프를 제작하였다. 정상상태 반응 시험 결과 2자유도 차량 모델과 7자유도 차량 모델의 결과는 매우 유사한 오차 값을 보였고, Full 차량 모델의 경우 오차의 최대 피크가 매우 큰 것을 확인하였으며 안정화 속도 또한 느린 것을 확인하였다.
이 논문에서 사용된 제어기는 2자유도 차량 모델을 기반으로 교육되었다. 2자유도와 7자유도 차량 모델의 경우 수학적으로 밝혀진 화이트 박스 모델이다. Full 차량 모델의 경우 모든 영향 변수(ex, 차량과 도로 사이의 마찰계수, 현가장치 등)를 고려하기 때문에 Full 차량 모델 거동이 단순한 2-Dof 및 7-Dof 모델보다 더 복잡하고 오차를 많이 나타낸다. 하지만 제어기가 이러한 영향 변수들을 제외한 2자유도에서 교육되어 Full 차량 모델에서는 좋은 성능을 보이지 못한 것으로 보인다.
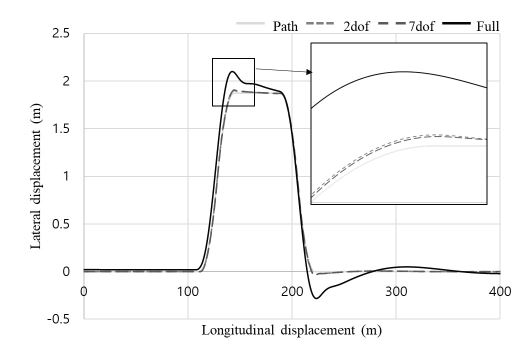
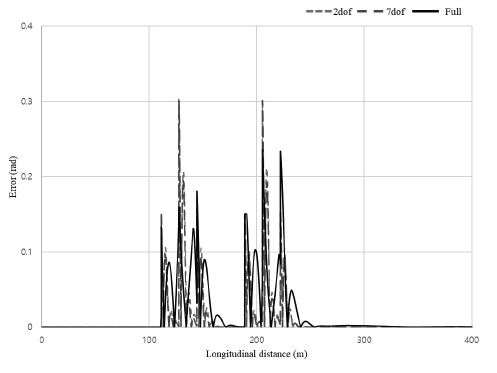
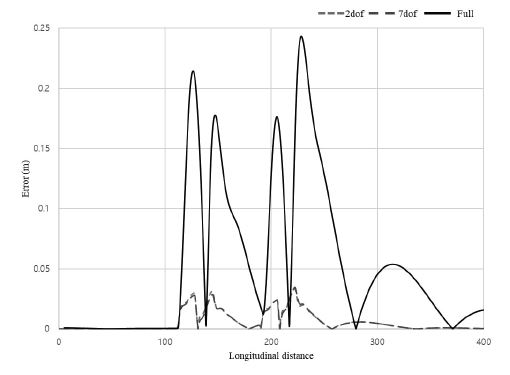
2 dof, 7 dof, Full 차량 모델의 Double lane change test 시험 결과를 Figs. 15~17에 제시하였다. Fig. 15에서 Double lane change test의 궤적을 모든 자유도의 모델이 제어가 가능한 것을 확인하였다. Fig. 16에서 각도 오차를 계산하기 위해 식 (24)을 사용하여 각도 오차 eθ(k)의 절댓값 그래프를 제작하였다. 과도 응답 반응 시험 결과로는 모든 자유도의 각도 오차 결과가 매우 유사한 오차 값을 보였다. Fig. 17에서 거리 오차를 계산하기 위해 식 (25)를 사용하여 거리 오차 ed(k)의 절댓값 그래프를 제작하였다. 정상상태 반응 시험 결과 2자유도 차량 모델과 7자유도 차량 모델의 결과는 매우 유사한 오차 값을 보였지만 Full 차량 모델의 경우 오차의 최대 피크가 매우 큰 것을 확인하였다.
정상상태 응답과 마찬가지로 과도 응답에서도 2자유도에서 제어기를 사용하였기 때문에 Full 차량 모델에서는 좋은 성능을 보이지 못한 것으로 보인다. 하지만 주파수 반응과 유사한 데이터를 교육데이터로 사용하여 정상상태 응답보다는 좋은 성능을 보이는 것으로 생각된다.
5. 결 론
이 논문에서는 2자유도 모델을 사용하여 제어에 사용되는 변수들을 정의하였다. 정의한 변수들 중 거리 오차 ed(k)와 각도 오차 eθ(k)를 뉴럴 네트워크의 입력 변수로 사용하였다. 문헌 연구를 통해 뉴럴 네트워크의 입력 변수를 변화시키고 가중치 업데이트 식을 생성하여 실시간으로 PID 계수를 변화시켜 궤적을 추종하는 오토 튜닝 PID 제어기를 제시하였다.
문헌 연구를 통해 궤적 추종 제어의 정상상태 응답을 확인하기 위한 R=100 m의 일정한 곡률 반경을 가진 궤적과 과도 응답을 확인하기 위한 Double lane change test 궤적을 정의하였다.
2자유도 모델을 사용하여 기존의 제어 방법(PID를 도로와의 거리 오차를 사용한 방법, PID를 도로와의 거리 오차와 각도 오차를 사용한 방법, 뉴럴 네트워크를 도로와의 거리오차만을 사용한 방법)과 이 논문에서 제안한 제어를 전체 궤적, 거리 오차, 각도 오차의 그래프로 비교하여 제어의 성능을 검증하였다. 또한 2자유도, 7자유도, Full 차량 모델을 사용하여 다양한 차량 모델에서도 사용할 수 있다는 것을 확인하였다.
하지만 2자유도에서 교육시킨 제어기로 제어를 수행하였기 때문에 2자유도와 달리 더욱 다양한 변수들이 존재하는 Full 차량 모델의 경우 제어 성능이 떨어지는 것을 확인할 수 있었다. Full car 모델을 사용하여 제어기를 교육시키는 추후 연구가 필요하다. 또한 다양한 교육 데이터에 대한 성능 변화에 대한 추후 연구가 필요하다.
References
- A. N. Ponce, A. A. Behar, A. O. Hernandez and V. R. Sitar, “Neural Networks for Self-tuning Control Systems,” Acta Polytechnica Vol.44, No.1, pp.49-52, 2004.
-
R. Hernández-Alvarado, L. G. García-Valdovinos, T. Salgado-Jiménez, A. Gómez-Espinosa and F. Fonseca-Navarro, “Neural Network-based Self-tuning PID Control for Underwater Vehicles,” Sensors, Vol.16, No.9, 2016.
[https://doi.org/10.3390/s16091429]

-
G. Han, W. Fu, W. Wang and Z. Wu, “The Lateral Tracking Control for the Intelligent Vehicle Based on Adaptive PID Neural Network,” Sensors, Vol.17, No.6, 2017.
[https://doi.org/10.3390/s17061244]

-
R. Rajamani, Vehicle Dynamics and Control, 2nd Edn., Springer, Berlin, 2012.
[https://doi.org/10.1007/978-1-4614-1433-9]

-
L. Li, G. Jia, J. Chen, H. Zhu, D. Cao and J. Song, “A Novel Vehicle Dynamics Stability Control Algorithm Based on the Hierarchical Strategy with Constrain of Nonlinear Tyre Forces,” Vehicle System Dynamics, pp.1093-1116, 2015.
[https://doi.org/10.1080/00423114.2015.1025082]

-
H. B. Pacejka and E. Bakker, “The Magic Formula Tyre Model,” Vehicle System Dynamics, Vol.21, pp.1-18, 1992.
[https://doi.org/10.1080/00423119208969994]

- D. L. Elliot, A Better Activation Function for Artificial Neural Networks, Institute for Systems Research Technical Reports, 1993.
- International Standrad, ISO/DIS 4138 Passenger Cars - Steady-state Circular Driving Behavior - Open- Loop Test Procedure, Second Edition, 1996.
- International Standrad, ISO/DIS 3888-1 Passenger Cars - Test Track for a Severe Lane-change Manoeuvere - Part 1: Double Lane Change, Second Edition, 2018.