An Optimal Design of CFRP Prepreg Laminates for Automotive Roof Considering Structural Stiffness and Formability
Copyright Ⓒ 2020 KSAE / 179-10
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
In recent years, an increasing number of automotive parts are being developed using Carbon Fiber Reinforced Plastics(CFRP) to improve fuel efficiency. Optimal design in various aspects must be developed in order to apply CFRP that have many design variables to actual parts. This study proposed an optimal design method for CFRP prepreg laminates for automobile roof models considering both structural stiffness and formability. First, the various fiber orientations of CFRP prepreg laminate plies were investigated based on DOE, and fiber orientations that gave the best structural stiffness were selected. Next, a draping analysis was conducted to investigate the fiber orientations of the CFRP prepreg laminate plies that could yield the least forming defects. Through this procedure, conditions for CFRP blanks that satisfy both structural stiffness and formability properties were determined. In addition, the blank holder and blank shape used in the draping process have been optimized to improve formability and reduce material costs. The present optimization method that considers both structural stiffness and formability could be utilized in the development of CFRP material-based parts.
Keywords:
CFRP, Optimal design, Laminate, Stiffness, Formability, Prepreg1. Introduction
As regulations on automobile fuel economy and emissions are being implemented worldwide, the global interest in lightweight materials and related research are constantly increasing as well. Among various lightweight materials, carbon fiber-based composite materials, which have high stiffness and high elasticity compared to steel-based materials, are currently attracting attention as one of the representative lightweight materials.1) Carbon fiber composites have traditionally been used exclusively in high value-added industries, such as the aerospace industry or race car industry, due to the high raw material prices. However, its application to structural materials and various parts of automobiles has lately been expanded mainly in Europe because of the advantages of carbon composite materials.2)
Among several types of carbon fiber composite materials available today, CFRP, which is composed of continuous fiber-based prepreg ply, has some distinctive features in which the mechanical properties are determined in varying forms depending on the direction of ply fibers and the number of laminates. However, in order to apply CFRP with many design variables to the actual parts, optimization in various aspects must be preceded.3) This is because optimization, while considering only the mechanical properties such as stiffness, may guarantee the possibility of developing parts to which CFRP is applied, but mass production may fail due to the limitations in either formability or economy. Even if the CFRP material and manufacturing process are optimized to ensure formability or economic efficiency, it may still fail to replace the existing materials due to insufficient stiffness and strength of the developed parts. Nevertheless, there have been few studies conducted on how to design an optimal CFRP part while considering both mechanical and manufacturing characteristics. Therefore, this study proposes a CFRP prepreg laminate ply design method that can optimize both the structural stiffness and the formability of the parts for models that are designed as roofs of automobiles.
The development of automotive parts using CFRP requires several aspects of optimization at the design stage. First, it must have a sufficient degree of stiffness to replace the existing steel material. For this purpose, an optimal design of the fiber orientation of each ply constituting the CFRP laminate is required. Second, there is a need for an optimal design of the fiber direction of the ply that can prevent fractures or wrinkles during the forming process so that no problem will occur when forming CFRP as a part. Third, it is necessary to optimize the number and tension of the spring holders that control material inflow during the forming process. Fourth, the initial shape of the CFRP blank must also be optimized in order to improve economic efficiency through material yield. In this study, optimal design was performed on the roof model of automobiles from various viewpoints so that it can be used for the development of various CFRP application parts in the future.
2. Laminate Pattern Optimization of CFRP Laminate
2.1 Laminate Pattern Selection Considering Structural Stiffness
In this study, the CFRP laminate is manufactured by laminating unidirectional (UD) plies composed of carbon fiber and resin combinations. Here, the mechanical properties of the individual ply appear as the sum of the carbon fiber properties and the resin properties. In particular, the UD carbon fiber orientation has a substantial effect on the stiffness of the ply, thereby suggesting that the stiffness of the CFRP ply in the carbon fiber direction shows a large value, but the stiffness in the vertical direction of the carbon fiber shows a small value because the stiffness of the resin was reflected. As such, when the orthotropy of the strength or stiffness of the CFRP ply is severe, the structural strength or stiffness of the CFRP ply is weak against a load applied from a direction other than the carbon fiber direction, which again makes it difficult to design a CFRP-based product. In order to avoid this problem, UD plies having various carbon fiber orientations should be laminated evenly over several sheets to produce CFRP with reduced orthotropy.
The mechanical properties of the CFRP UD ply can be expressed by the following stress-strain relationship when considering orthotropy due to carbon fiber arrangement and assuming a plane stress condition4) (1 indicates the fiber direction and 2 indicates the vertical direction to fiber).
| (1) |
(However, according to the Maxwell-Betti reciprocal theorem)
The mechanical properties of a CFRP laminate with multiple UD plies are determined by combining the properties of each ply. The resulting stress-strain relationship of the CFRP laminate can be approximated by using the classical lamination theory.4) However, in this study, it was calculated by using Altair's OptiStruct, a commercial finite element analysis program.5) The data shown in Table 1 on Toray's T700 class UD ply was used as the structural property value of the UD ply.
The stiffness of the CFRP laminate is determined by combining the fiber directions of the ply constituting the laminate, namely, the laminate pattern. Therefore, it is necessary to calculate the stiffness of the CFRP laminate according to the laminate patterns, and select a suitable one to be used as a roof of an automobile based on this.
If the fiber directions of the ply to be laminated are too diverse, the number of possible laminate patterns would be too high, thus making it impractical to manufacture the laminate. It was therefore assumed in this study that the CFRP laminate for automobile roof is manufactured as a laminate of four plies, and designable laminate patterns were derived by using the design of experiment (DOE). It was also assumed that the fiber direction of the standard UD ply is set to 0° and the vertical direction of the fiber is set to 90°. In addition, when the fiber direction of the ply constituting the laminate is biased, the orthotropy of the laminate becomes severe. In order to avoid this, all four plies were selected to have different fiber directions. In this case, the number of laminate patterns is 4 × 3 × 2 × 1 = 24.
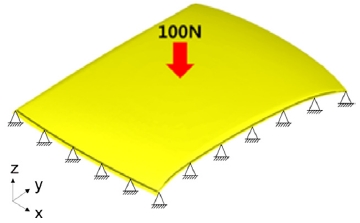
Structural analysis was performed for each case, assuming that the roof shape model shown in Fig. 1 is a laminate consisting of one of these 24 laminate patterns. It was also assumed that the boundary condition was applied to the edge of the roof model by reflecting the condition in which the roof was fixed to the vehicle body, and that a load of 100 N was applied to the center in a vertical direction. Table 2 shows all the laminate patterns and the displacement of the load points obtained through the structural analysis for each. Since it is assumed that the same load is applied, the stiffness of the roof model according to the laminate pattern can be compared with each other through load point displacement.
When comparing the displacement of each laminate pattern in Table 2, the smallest value of approximately 6.75 mm was found in #6, which led us to conclude that the stiffness is the largest. Overall, it was observed that the stiffness is relatively excellent if the UD plies are laminated in a way that would reinforce weak properties in the vertical direction of fibers, such as [0/90], [90/0], [45/-45], and [-45/45] when manufacturing a roof shape.
If only stiffness is considered, one laminate pattern that exhibits the smallest displacement among the above results can be selected. However, a laminate pattern other than those that maximize stiffness may be more suitable in terms of formability or other aspects. In view of this, the top 8 laminate patterns in the order of stiffness, particularly with small displacement against the load, were selected as candidate groups in this step before being reviewed in the following other criteria optimization.
2.2 Laminate Pattern Selection Considering Draping Formability
In this study, the CFRP laminates are manufactured in a prepreg form before being converted into final products by means of press-type forming and curing processes. At this time, the forming behavior of CFRP prepreg appears as a combination of the carbon fiber forming behavior and the resin molding behavior. In particular, the forming process is affected by several material properties, such as the stiffness of the carbon fiber, as well as the viscoelasticity of the resin, while its properties exhibit nonlinearity. In general, it is quite difficult to accurately measure the forming property values compared to the structural stiffness values. However, it can be said that the forming of the CFRP prepreg laminate prior to the completion of curing, particularly draping, is primarily determined by the forming behavior of the fibers. It was therefore determined that the results of the CFRP prepreg laminate sheet drape were sufficiently predictable even if only the physical properties of the carbon fiber were considered without taking into account the molding properties of the resin, such as viscosity and curing behavior. For this reason, CFRP prepreg laminate draping analysis was performed in this study by using ESI's composite material forming analysis program, PAM-FORM.7) As shown in Table 3, PAM-FORM MAT LIBRARY data were used for the forming properties at this time.
Previously, the top 8 laminate patterns based on stiffness were derived from DOE and structural analysis with their laminate patterns, as shown in Table 4. For the CFRP laminate with these laminate patterns, the draping analysis of the roof model was performed, and the deformation behavior of the laminate and carbon fiber was investigated.
In regard to the draping of the CFRP prepreg laminate, the amount of fiber inflow or fiber rotation may vary based on the forming shape. Since this difference accumulates in the intra-ply or inter-ply, wrinkles or fractures of the CFRP laminate may occur, which is a defect in the forming of the product.8,9) In order to predict such defects in the forming, appropriate formability evaluation indicators are needed. Since the formability evaluation indices for the CFRP prepreg laminate have not yet been established, the evaluation indices were selected as follows by referring to the evaluation indices of the metal sheet.
The wrinkle area, shear angle, and fiber vertical strain (fiber 2 strain) were selected as appropriate indicators for evaluating formability. Those values can be confirmed from the results of the draping analysis of the CFRP prepreg laminate. The values of each index obtained from the draping analysis are shown in Table 5, with the values being slightly different depending on the laminate pattern. Based on these values, it is possible to select the laminate pattern with the best formability. Considering both the stiffness value of the structural analysis side reviewed above and the value of the formability evaluation index reviewed at this time, a specific laminate pattern that can equally improve stiffness and formability can be selected. It is observed that #20 is the optimal laminate pattern when the weighting of stiffness and formability are applied equally to 0.5.
3. Optimization of Blank Holder for CFRP Laminates
3.1 Design of Spring Holder for Blank Inflow Control
Wrinkles or fractures occurring during the forming process of the laminate are the cause of product defects. A method of suppressing the occurrence of wrinkles by using a blank holder is generally used to solve this problem with many studies conducted in order to optimize the conditions of the blank holder.10) Furthermore, the blank holder of the general method requires an additional material area that can be held in addition to the area of the blank that becomes the final product. The material in this area is cut through the trimming process after the forming process, thereby increasing the manufacturing cost due to material loss. It is also necessary to install a device that can physically fix the material and apply tension, thereby increasing manufacturing cost. In general, CFRP laminate has a higher material cost than metal sheets, and it is more susceptible to material damage when held. Therefore, it is recommended to use spring holders instead of blank holders that require a large pressing area. The spring-loaded clamping method reduces these problems and improves formability by mitigating the shear deformation of fibers. As a result, the process is being applied to mass production in some composite parts manufacturing companies.11)
3.2 Spring Holder Optimization
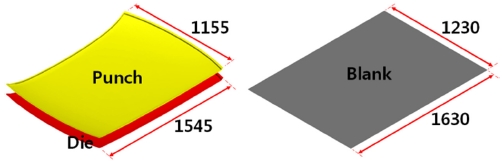
In order to optimize the roof of an automobile made of CFRP laminate, it is also necessary to optimize the blank spring holder required for the forming process. For this spring holder optimization, the shape of the punch/die set and the blank for the roof model were designed as shown in Fig. 2. The forming behavior was evaluated by changing the number of spring holders, clamping area, and spring tension, respectively. Since there are many variables of spring holders to be considered, only one case was considered for the laminate pattern of the CFRP laminate blank. Specifically, #20 or [90/0/-45/45], which was predicted to be the best when stiffness and formability were considered at the same time, was assumed as the laminate pattern of the CFRP laminate blank.
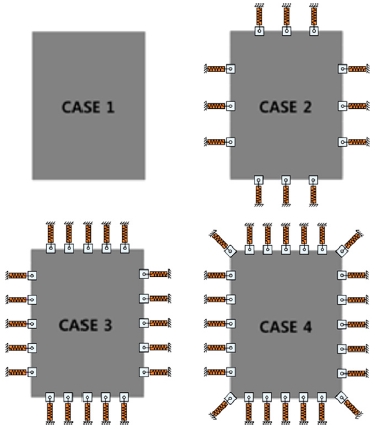
First, in order to evaluate the forming behavior according to the number of spring holders, the four cases shown in Fig. 3 were considered. Table 6 shows the formability evaluation index values for each case obtained by forming analysis. Based on the index values, it appears that the wrinkle area has been slightly increased by applying the spring holder compared to the condition without the holder, but the shear angle and the fiber vertical strain can be reduced. In other words, it seems that the application of the spring holder plays a role in suppressing the concentration of stress. The comparison of the evaluation index values for each case with a relative ratio showed a disadvantage in that the wrinkle area slightly increased in Case 3, but the two indices of shear angle and fiber vertical strain have the advantage of being minimal. In view of this, Case 3, which applies five to each of the four straight edges of the square blank (5 × 4 = 20 spring holders), is considered to be the optimal configuration in terms of the number of spring holders.
Second, in order to evaluate the forming behavior according to the clamping area of the spring holder, the six cases shown in Fig. 4 were considered. Forming analysis was performed under the six clamping area conditions of 10, 20, 30, 50, 100, and 200 mm2, and the resulting formability evaluation index values are shown in Table 7. Based on the index values, it seems that Case 4 and Case 5 show relatively small values for the wrinkle area, which is advantageous. In the shear angle, Case 3 and Case 4 have relatively small values, while in the vertical direction of the fiber, Case 2 and Case 3 have relatively small values, which appear to be advantageous. Based on these results, the formability conforming to the clamping area of the spring holder may vary in superiority and inferiority according to each index. It is determined that Case 2 (20 mm2 area), Case 3 (40 mm2 area), and Case 4 (50 mm2 area) can be considered as the optimal clamping areas.
Third, in order to evaluate the forming behavior according to the spring tension, a forming analysis was performed by applying six spring tensions of 100, 200, 300, 500, 700, and 1000 N. In this case, the number of spring holders was assumed to be 5 × 4 = 20, which is an optimal configuration, and 50 mm2 was selected from the three optimal candidates obtained earlier for the clamping area. The resulting formability evaluation index values are shown in Table 8. Based on the index values, Case 5 and Case 6 are the most advantageous for the wrinkle area. Only Case 6 has a relatively large value for the shear angle, and the other cases are similar. In addition, it appears that Case 5 is the least advantageous in terms of strain in the vertical direction of the fiber. A comprehensive comparison of the formability index values such as this shows that Case 5 with a spring tension of 700 N can be considered as the optimal tension.
4. Optimization of the Blank Shape of CFRP Laminates
4.1 Blank Shape Optimal Design Method
Since CFRP laminate has a very high material price compared to general steel sheets, lowering the amount of trimmed material after product forming is very important in order to warrant the economic feasibility of the mass production of CFRP products. In order to minimize the amount of material to be trimmed, the initial blank shape should be designed so that the shape after product forming using the CFRP laminate is as similar as possible to the final product shape. Since the optimal design of the initial blank shape helps to improve the formability and economic efficiency of the product, many studies have been conducted in sheet metal forming. However, a systematic study case for the forming of CFRP laminates has not yet been conducted. Therefore, an optimal design of the shape of the CFRP laminate blanks was attempted for an automobile roof model in this study.
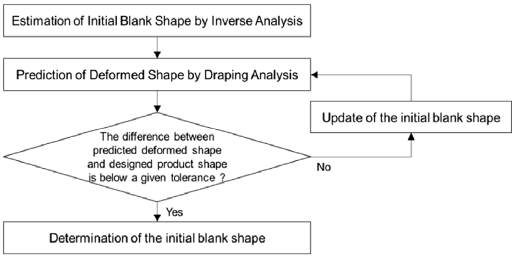
The optimal design method pursued in this study was an iteration of the following two steps based on the finite element analysis of the draping of CFRP laminates. The first step is to evaluate the accuracy of the estimated blank shape by performing a forming analysis using the estimated blank shape and then comparing the result with the design product shape. The second step is to estimate a new blank shape by using an appropriate algorithm when it is determined that the accuracy of the estimated blank shape is low based on the forming analysis result. In the end, an optimal blank shape can be obtained by repeating the aforementioned two steps until it is determined that the accuracy of the estimated blank shape is sufficiently high. Since it is not easy to make an initial estimate of the blank shape, HyperWorks' inverse analysis function was used. Inverse analysis results alone do not yield the optimal blank shape immediately, but they are useful for obtaining an initial estimate of the blank shape. The optimal design process described above is shown in the Fig. 5 flow chart.
4.2 Blank Shape Optimal Design Result
In the blank optimal design stage, a reference figure is necessary for calculating the difference between the predicted forming shape and the design product shape. With this criterion, the authors considered the line segment of the outline representing the blank border, and the node placed on the blank border when the blank is modeled as a finite element. Using these two reference figures, the difference in shape was calculated in the following three methods and the reference shape is used when updating the blank shape.
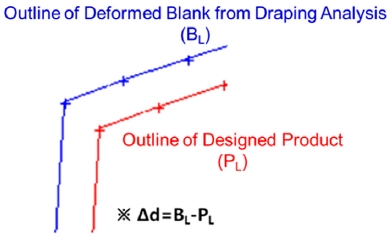
In the first method, the difference in shape was calculated based on the distance between the straight lines, which is the line segment constituting the outline, for both the shape predicted by the forming analysis and the design product shape. When updating the blank shape, the position of the straight line consisting of the outline was corrected based on the calculated shape difference. Since both the calculation and update of the shape difference use the shortest distance between the straight lines, this is called the line offset method. As shown in Fig. 6, the line offset method repeatedly updates the position of the straight line so that the distance between the blank outline (BL) and the product outline (PL) obtained by forming analysis becomes less than a certain value in order to obtain the optimal blank shape. When the blank shape was initially estimated, inverse analysis was used. When the forming analysis was performed with the assumption of the blank shape obtained by inverse analysis, an error occurred with the product shape. This inverse analysis error was larger than that of the sheet metal forming. This may be caused by an inappropriate mesh size used or not reflecting the coefficient of friction properly in the inverse analysis. In particular, it is evident that this problem is more pronounced in the inverse analysis of the CFRP laminate forming. It was corrected by moving the outline of the blank until the difference between the shape predicted via forming analysis and the shape of the designed product became less than a specific level.
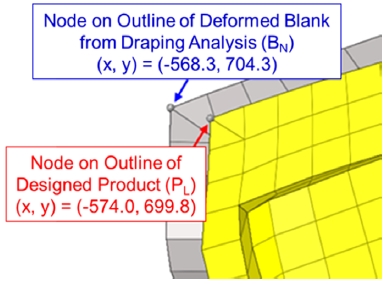
In the second method, the shape difference is calculated based on the distance between the nodes located in the outline of the finite element model for both the shape predicted via forming analysis and the designed product shape. And the location of the nodes was modified based on the calculated shape difference when the blank shape is updated. Since the shortest distance between the nodes is used for both calculation and update of the shape difference, this is called the node offset method. As shown in Fig. 7, the node offset method extracts the x and y coordinates of the nodes on the blank outline (BN) and the nodes on the product outline (PN) obtained via forming analysis, respectively, and it uses the distance difference to determine the difference of shape. In order to update the blank shape, the position of the node on the outline was moved and corrected.
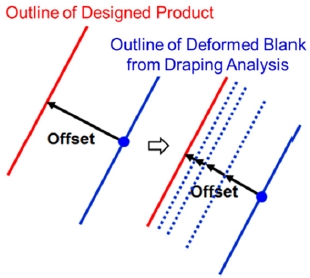
Based on the performance comparison of the two methods above, the straight line offset method has the advantage of quickly correcting the blank shape by moving the entire straight line, but there is a disadvantage in finely modifying the shape. On the other hand, the node offset method has the advantage of being able to finely modify the shape because it modifies the blank shape by moving each node, but there is a disadvantage that the process becomes complicated because the coordinate values of each node must be manually modified. Therefore, the following third method was introduced in order to utilize the advantages of both methods. In this method, the shape predicted by the forming analysis uses the outline nodes of the finite element model, and the designed product shape uses the straight line constituting the outline. The difference in shape was calculated based on the distance between the nodes and the straight line. In addition, the update of the blank shape was based on the nodes. Since this method uses both a node and a straight line (e.g., calculating the shortest distance from a node to a straight line), it is called the node-to-line offset method.
In the node-to-line offset method, the initial blank shape was first derived through inverse analysis, and the draping analysis was performed by using this. As a result, there is a difference between the formed shape and the designed product shape, as shown in Fig. 8, when the initial blank shape was applied.
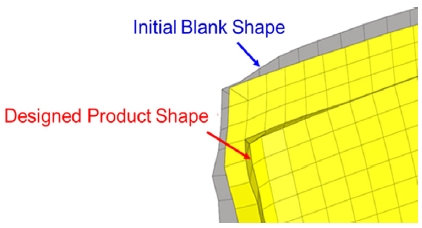
Comparison of draping analysis results using the estimated initial blank shape and designed product shape
The shortest distance between the outline node of the shape obtained via forming analysis and the outline of the product shape was measured. In order to reduce the difference between these shapes, the blank outline node was moved by 50 % of the measured distance, as shown in Fig. 9, and the forming analysis using the modified blank was again performed. Other ratios were available instead of 50%, which is the ratio of movement to distance, but there was a difference in the speed at which the difference in shape decreases.
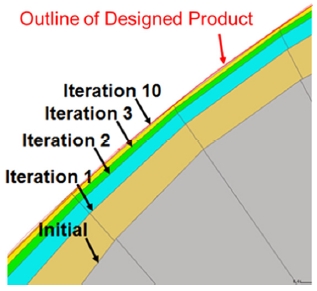
A total of 10 iterative forming analyses and blank shape updates were performed, and the changes of the blank shape obtained in each iteration are shown in Fig. 10. It is evident that it starts from the initial blank shape and gradually converges to the product shape.
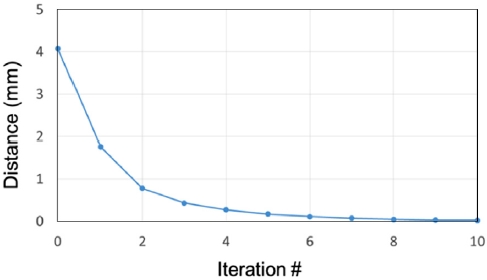
As shown in Fig. 11, the trend of the maximum value changes among the shortest distances of the outline node of the shape and the straight line of the product outline obtained by forming analysis using the updated blank shape over a total of 10 iterations. If convergence is assumed to have been achieved when the shape difference with the product is less than 0.5 mm, it is evident that the desired initial blank shape can be derived only by performing three iterations. Among the three initial blank shape optimal design methods conducted in this study, the node-to-line offset method is found to be the best not only in the efficiency of the calculation procedure, but also in the accuracy of the optimal design result.
5. Conclusions
In this study, the optimal design of CFRP prepreg laminate was pursued with the aim of developing automobile roof using CFRP laminate. First, a candidate group of laminate patterns that can reduce the stiffness and strength orthotropy of the laminate was derived by intersecting the fiber directions of the UD ply for application to vehicle body structural components, such as automobile roofs. Based on this, laminate patterns that optimize the structural stiffness of the CFRP laminate were selected in order to replace the existing steel material and achieve weight reduction. In addition, laminate patterns were selected in order to optimize the draping formability of the CFRP prepreg laminate in consideration of the difficulty of forming CFRP and economic efficiency. Through this process, an optimal laminate pattern was designed that satisfies both aspects of structural stiffness and formability.
In order to improve formability, optimal values of the number of spring holders, clamping area, and spring tension that additionally control the amount of blank inflow were derived. Furthermore, the shape of the CFRP laminate blank was optimized by applying the node-to-line offset method to improve the economy and formability when CFRP is applied.
This study suggested a whole-cycle optimization strategy for CFRP prepreg laminates. Based on the analysis results, the optimal laminate conditions can vary according to the criteria of structural stiffness, formability, blank holder, and blank shape. Therefore, the optimization results vary depending on the criteria used in design. In the case of optimization that considers various purposes at the same time, the designer's judgment eventually plays an important role. In this study, the result when structural stiffness and formability are reflected in equal weights was presented as a case study.
However, optimization of the blank holder and the blank shape was performed only for the condition of the finally selected laminate in consideration of structural stiffness and formability for convenience. The roof model is a shallow square cup drawing shape with large forming defects mainly occurring in the corners or corner areas of the square cup. These forming defect areas remain after trimming and they are included in the shape of the part. If the blank holder and blank shape are changed, the extent of forming defects may vary slightly, so the ranking of the optimal laminate evaluated in terms of structural stiffness and formability for the initial blank may similarly change. However, if the change is not large, it may be an efficient strategy to first determine the optimal laminate condition for the initial blank in consideration of structural stiffness and formability, and to optimize the blank holder and blank shape for that condition. Of course, it is necessary to secure the reliability of the optimization result by re-evaluating the structural stiffness, formability, and blank holder perspective after the optimal blank shape has been derived in order to verify the effectiveness of the initially obtained optimal laminate condition. If the initially obtained optimal laminate condition is no longer in excellent condition due to the change in the blank shape, the suggested optimization method will have to be repeated until a new optimal laminate condition is found. Since such iterative optimization can entail considerable amount of time and cost, further study is needed on how this process can be carried out efficiently.
Nomenclature
| ρ : | Specific density |
| E1 : | Young’s modulus in fiber direction |
| E2 : | Young’s modulus in lateral direction |
| G12 : | In-plane shear modulus |
| ν12 : | In-plane Poisson’s ratio 1 |
| ν21 : | In-plane Poisson’s ratio 2 |
| Fb1 : | Bending factor in warp direction |
| Fs1 : | Out-of-plane shear factor in warp direction |
| Fb2 : | Bending factor in weft direction |
| Fs2 : | Out-of-plane shear factor in weft direction |
| Fbm : | Bending factor of matrix in shear coupling |
| Fsm : | Out-of-plane shear factor of matrix in shear coupling |
Acknowledgments
This research was conducted with the financial support from the R&D Convergence Program of NST (National Research Council of Science & Technology) and the Basic Research Support Project of the Ministry of Education (NRF-2017R1D1A1B03029350) of the Republic of Korea.
References
- F. C. Campbell, Structural Composite Materials, ASM International, Ohio, 2010.
- A. Erber, “Function-integrated Lightweight Structure with Carbon Fiber Reinforced Thermoplastic Materials,” Werkstoff Forum, 2015.
- Y. J. Kim, Y. W. Jung and H. K. Kim, “A Study on the Automatic Optimization of CFRP Prepreg Laminates and Blank Shape,” KSAE Spring Conference Proceedings, p.1061, 2019.
- M. W. Hyer, Stress Analysis of Fiber-Reinforced Composite Materials, WCB McGraw-Hill, Boston, pp.148-347, 1998.
- ALTAIR, https://www.altair.com/optistruct, , 1994.
- Wade and Feraboli, Simulating Laminated Composites using LS-DYNA Material Model dMAT54 Part I: [0] and [90] Ply Single-element Investigation, University of Washington, 2012.
- PAM-COMPOSITES 2018, PAM-FORM USER'S GUIDE, 2017.
- A. Willems, S. V. Lomov, D. Vandepitte and I. Verpoest, “Double Dome Forming Simulation of Woven Textile Composites,” Esaform Conference on Material Forming, 2006.
- M. Nishi, T. Hirashima and T. Kurashiki, “Textile Composite Reinforcement Forming Analysis Considering Out-of-plane Bending Stiffness and Tension Dependent,” Proceedings of the 16th European Conference On Composite Materials, pp.1-8, 2014.
-
H. Naceur, Y. Q. Guo and J. L. Batoz, “Blank Optimization in Sheet Metal Forming Using an Evolutionary Algorithm,” Journal of Materials Processing Technology, Vol.151, Nos.1-3, pp.183-191, 2004.
[https://doi.org/10.1016/j.jmatprotec.2004.04.036]

- S. Chen, Fabric Forming Simulation and Process Optimisation for Composites, Ph. D. Dissertation, University of Nottingham, Nottingham, 2016.
-
H. K. Kim, H. B. Shim, B. S. Cha, G. H . Song and H. J. Kim, “Optimization of Initial Blank Shape for Minimizing the Trimming Process in Hot Stamping of T-shaped Parts,” International Journal of Precision Engineering and Manufacturing, Vol.19, No.5, pp.721-728, 2018.
[https://doi.org/10.1007/s12541-018-0086-z]