스테빌라이저 바의 유연성을 고려한 버스 조종 안정성에 관한 연구
Copyright Ⓒ 2020 KSAE / 179-03
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
Many vehicles use stabilizer bars to increase the roll rate for satisfactory handling characteristics. Stabilizer bars are laterally mounted torsional springs that resist the vertical displacement of the wheels relative to one another. Vertical suspension rates are not increased when both wheels are deflected simultaneously; however, the stiffness of one wheel bump is increased. The analytical and experimental techniques for accurately estimating the roll stiffness of a stabilizer bar are presented in this paper. Three models of a stabilizer bar are designed as follows: torsional spring model, bushing model, and beam model. Based on quasi-static and vehicle dynamic analyses, we found that the beam model is the most efficient method to consider the twisting and bending of a stabilizer bar.
Keywords:
Stabilizer bar, Roll stiffness, Bump steer, Link error, Roll steer, Vehicle dynamics키워드:
스테빌라이저 바, 롤 강성, 범프 스티어, 링크 에러, 롤 스티어, 차량 동역학1. 서 론
차량의 개발 초기 단계에서 상품성을 토대로 동력 성능, 내구, NVH, 승차감 그리고 조종 안정성 등과 같은 성능들을 충분히 검토해야 하는데, 이 중 승차감과 조종 안정성은 운전자와 승객에게 매우 중요한 요소로 인식되고 있다. 승차감과 조종 안정성은 현가장치의 복잡한 설계 요소들에 의해 확보되는 동적 성능으로서, 이를 최적화하기 위한 설계 특성값들을 결정하기가 매우 어렵기 때문에 주로 실차 시험을 통한 튜닝(Tuning)에 의존하고 있다. 그러나 실차 시험을 통한 튜닝은 많은 시간과 비용이 소요될 뿐만 아니라 운전자의 숙련도에 의존하므로 시험 결과의 재현성 확보가 어렵다.
한편, CAE 관련 컴퓨터 기술의 급속한 발전에 따라 다물체 동역학 기법을 현가장치의 모델링 및 시뮬레이션에 적용하여 현가장치의 동특성을 분석한 후 보다 신속하고 정확한 설계 자료를 제공하는 것이 가능해졌다.1) 따라서 시제작 단계 이전에 차량의 동특성을 미리 예측하고 성능을 향상시키기 위해서는 전후 현가장치의 스프링(Spring), 쇽업소버(Shock absorber), 스테빌라이저 바(Stabilizer bar), 현가 링크(Suspension links), 부싱(Bushing), 액슬 궤적(Axle trajectory) 그리고 타이어 등에 대한 초기 설계 기본 자료들을 토대로 설계 변수의 변경이 용이한 다자유도를 갖는 현가장치 모델링이 필수적이다. 이중 스프링, 쇽업소버, 현가 링크, 부싱, 액슬 궤적 등은 비교적 쉽게 설계 자료로부터 얻을 수 있고, 타이어 역시 타이어 제작사의 실험 데이터를 적용할 수 있는 해석적인 타이어 모델이 구성되어 있으므로 모델링시 큰 어려움이 없지만, 스테빌라이저 바의 경우 비틀림과 굽힘 효과를 동시에 고려할 수 있도록 모델링 해야 하는 어려움이 뒤따른다.
스테빌라이저 바를 모델링 하는 기법으로 주로 사용되고 있는 방법으로는 스테빌라이저 바를 2개의 강체로 분리한 뒤 두 강체 사이를 회전 스프링으로 연결한 후 스테빌라이저 바 자체의 비틀림 강성을 적용하는 방법이 있다. 두 번째 방법으로는 3개 이상의 보 요소(Beam element)를 사용하여 비틀림과 굽힘을 동시에 고려한 모델링 기법이 있다.2) 세 번째 방법으로는 스테빌라이저 바의 마운팅 부싱을 수학적으로 모델링하여 힘과 처짐의 관계를 유도하여 스테빌라이저 바를 간편하게 모델링하는 방법이 있다.3)
본 논문에서는 스테빌라이저 바 고유의 롤 강성(Roll stiffness)을 적절히 구현하기 위해 보 요소의 개수에 따른 4가지 모델링 방법을 고려하였다. 그리고 스테빌라이저 바 단품의 롤 강성 시험 결과와 각 보 요소 모델의 롤 강성 해석 결과를 상호 비교하여 적절한 보 요소 모델링 방법을 제시하였다. 한편, 현가 기구 해석을 위한 스테빌라이저 바의 모델링 방법으로 회전 비틀림 스프링을 이용한 모델(이하 Kt model), 부싱 강성을 고려한 모델(이하 Bushing model) 그리고 보 요소를 이용한 모델(이하 Beam model)과 같은 3가지 기법을 이용하였으며, 3가지 현가 기구 모델에 대한 준정적 해석을 통해 기구 정역학적 특성들을 고찰하였다. 마지막으로 3가지 스테빌라이저 바 모델을 적용시킨 전체차량 모델을 구성하여 차선 변경 해석을 수행한 후, 해석 결과와 시험 결과의 비교 분석을 통해 기하학적 형상과 힘 전달 경로를 고려한 보 요소 모델링 기법이 스테빌라이저 바의 고유 특성을 잘 반영할 수 있는 방법임을 입증하였다.
2. 스테빌라이저 바의 거동 특성
2.1 고유 기능
스테빌라이저 바는 차체의 롤 발생을 억제하고 주행 안정성의 향상에 기여하는 새시 부품이다. 선회시 원심력의 작용에 의해 롤 운동이 발생하면 차체가 기울게 되고 이에 따라 스테빌라이저 바의 외륜쪽은 낮아지고 내륜쪽은 높아진다. 따라서 스테빌라이저 바의 양단이 반대 방향으로 회전하여 즉, 하중을 덜 받는 내륜쪽으로부터 반대 방향으로 회전함으로 인해 내륜쪽으로부터 외륜쪽으로 토크가 전달되어 과도한 변형을 막아준다.
또한 노면에 의해 한쪽 타이어만 높아지는 경우에도 선회시와 유사하게 스테빌라이저 바의 양단에서 비틀림각이 발생되고, 이에 의해 생성된 토크는 양쪽 타이어의 높이를 같게 하는데 기여한다. 결국 스테빌라이저 바는 차체와 타이어의 좌우 높이가 같은 경우 거동에 영향을 미치지 않으나, 차체와 타이어의 좌우에 편차가 발생하는 경우 즉, 롤이 발생하는 경우에는 차량의 거동에 중요한 영향을 미친다.
2.2 롤 강성
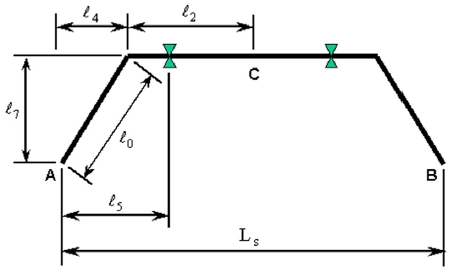
스테빌라이저 바의 이론적인 롤 강성은 Fig. 1에서와 같이 단순화된 스테빌라이저 바의 형상으로부터 유도할 수 있다.4) 일반적으로 스테빌라이저 바는 Fig. 1에 나타나 있듯이 비틀림 중심인 C 위치를 중심으로 좌우 대칭인 기하학적 배치를 갖고 있다.
따라서 비틀림 중심인 C 위치를 고정시키고 A 위치에서 가해지는 수직력 P와 이에 따라 발생되는 A 위치에서의 수직 변위의 관계로부터 스테빌라이저 바의 이론적인 롤 강성을 구할 수 있다. 수직력 P에 의해 A 위치에서 발생되는 수직 변위는 다음 식 (1)과 같다.
| (1) |
여기서 I는 면적 관성 모멘트이며, 원형 단면의 경우 으로 정의된다.
결국, 스테빌라이저 바의 이론적인 롤 강성은 다음 식 (2)와 같이 유도할 수 있다.
| (2) |
2.3 보 요소
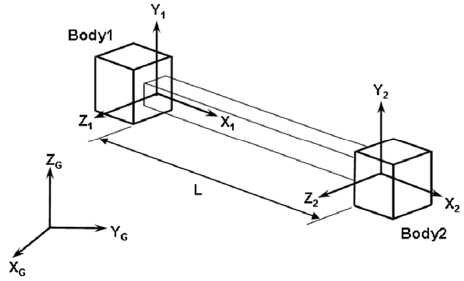
보 요소는 Fig. 2에 나타나 있듯이 절점 2에 대한 절점 1의 병진 및 회전 굽힘에 대한 응답으로서, 절점 1에 축력(Axial forces), 국소 y축과 z축에 대한 굽힘 모멘트, x축에 대한 비틀림 모멘트, 그리고 전단력(Shear forces)과 같은 힘들을 적용시킨다.
따라서 보 요소의 선형 구성 방정식은 다음 식 (3)과 같이 정의할 수 있다.5)
| (3) |
where K11 = EA/L
K22 = 12EIzz[L3(1+Py)]
K26 = -6EIzz[L2(1+Py)]
K33 = 12EIyy[L3(1+Pz)]
K35 = 6EIyy[L2(1+Pz)]
K44 = GIxx/L
K55 = (4+Pz)EIyy/[L(1+Pz)]
K66 = (4+Py)EIzz/[L(1+Py)]
Py = 12EIzzβy/(GAL2)
Pz = 12EIyyβz/(GAL2)
y방향 전단 면적비(Shear area ratio)
z방향 전단 면적비(Shear area ratio)
ζ:감쇠비(Damping ratio) (0 < ζ < 1)
2.4 강성 해석 모델링
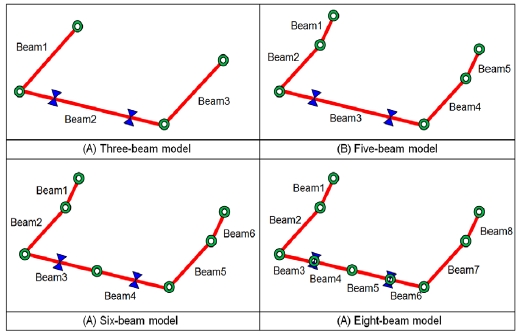
본 논문에서는 스테빌라이저 바의 강성 해석 모델을 구성하기 위해 식 (3)에서와 같은 선형 구성 방정식을 갖는 보 요소 모델링 방법을 적용하였다. 따라서 스테빌라이저 바의 기하학적 형상과 보 요소의 힘 전달 특성을 고려하여 Fig. 3에서처럼 보 요소의 개수를 3개, 5개, 6개, 8개로 늘려가면서 강성 해석 모델들을 구성하였다.
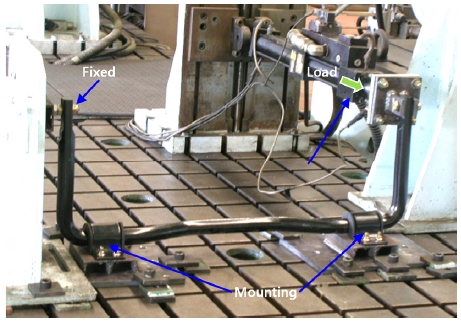
한편, 4가지 방법으로 구성된 강성 해석 모델의 롤 강성값의 유효성을 검증하기 위해 Fig. 4와 같은 한 끝 단 고정용 지그(Jig), 좌우 마운팅 지그, 유압 액츄에이더(Hydraulic actuator)로 구성된 스테빌라이저 바의 롤 강성 시험기를 제작하여 실제 단품에 대한 롤 강성 시험을 수행 하였다.
스테빌라이저 바의 롤 강성 시험에서는 스테빌라이저 바의 한 끝 단은 고정용 지그에 부착시킨 후, 유압 액츄에이더를 이용하여 다른 끝 단에 0에서 138 kgf까지 힘을 증가시키면서 그에 따른 변위를 측정하였다.
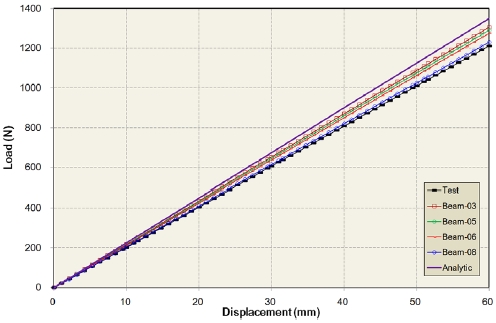
또한 4가지 강성 해석 모델에도 롤 강성 시험에서와 동일한 경계 조건을 부가하여 하중 vs 변위 관계 및 롤 강성을 검토하였으며, 그 결과는 Fig. 5와 Table 1에 각각 나타내었다.
Table 1로부터 식 (2)에 대한 이론적인 롤 강성값은 시험 결과와 6.8 % 정도의 오차를 보였다. 또한, 3개, 5개, 6개의 보 요소를 사용한 강성 해석 모델들의 롤 강성값들은 비슷한 경향을 보였으나, 시험 결과와는 4.1 % 정도의 오차를 나타냈다. 그러나 8개의 보 요소를 사용한 강성 해석 모델의 롤 강성값은 실제 강성값과 거의 동일한 결과를 나타내었다.
따라서 고유 형상과 힘 전달 경로를 고려한 8개의 보 요소 강성 해석 모델이 스테빌라이저 바의 고유 특성을 잘 반영한다고 판단할 수 있다.
2.5 전륜 현가장치의 기구 해석
스테빌라이저 바의 고유한 롤 강성을 구현하기 위한 보 요소의 유효 개수는 2.4절에서 결정되었으므로, 본 절에서는 전륜 현가장치의 기구 해석 시 필요한 스테빌라이저 바의 모델링 방법들을 고찰하였다.
현가 기구 해석에 적용될 스테빌라이저 바의 모델링 방법으로는 비틀림 회전 중심에 회전 스프링을 적용하는 Kt model, 회전 중심과 프레임 마운팅 위치에 부싱을 적용하는 Bushing model, 그리고 8개의 보 요소를 적용하는 Beam model과 같은 3가지 방법을 고려하였다.
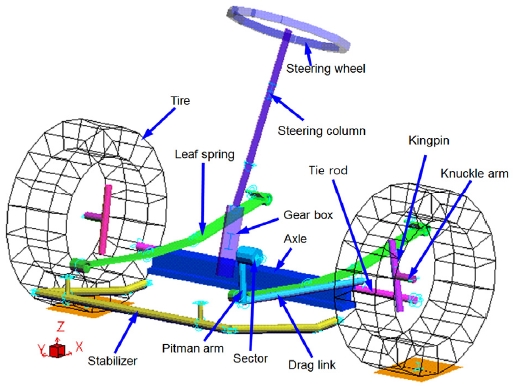
전륜 현가장치의 준정적 기구 해석 모델은 범용 동역학 해석 프로그램인 ADAMS를 이용하여 조향계와 3가지 스테빌라이저 바 모델들을 각각 포함한 현가계로 구성하였으며, Fig. 6에 한 예를 나타내었다.
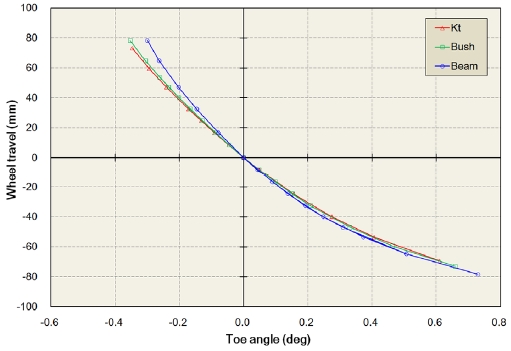
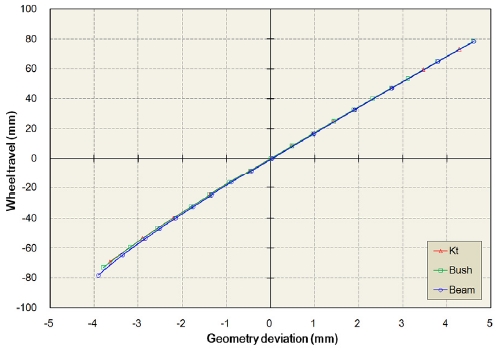
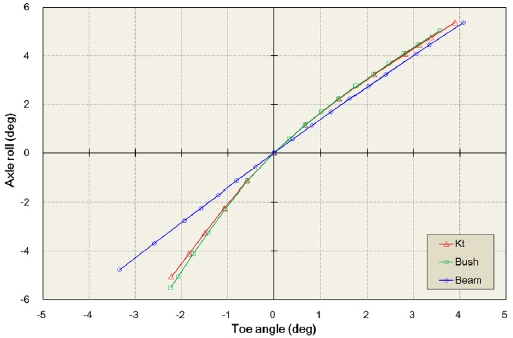
전륜 현가장치의 준정적 기구 해석에서는 양쪽 바퀴의 동위상 운동(In-phase motion)과 역위상 운동(Out-of-plane)시 바퀴와 액슬의 궤적을 검토하였다. 동위상 운동시에는 범프 스티어(Bump steer)와 링크 에러(Link error), 역위상 운동시에는 롤 스티어(Roll steer) 현상을 고찰하였으며, 그 결과는 Figs. 7~9에 나타내었다.
Kt model과 Bushing model은 범프 스티어, 링크 에러 그리고 롤 스티어 특성에 거의 동일한 경향을 나타냈다. 한편, Beam model은 범프 스티어와 링크 에러의 경우에는 다른 두 모델들과 거의 유사한 경향을 보였지만, 롤 스티어의 경우에는 리바운드 시 다른 두 모델에 비해 더 큰 값을 나타냈다. 이를 통해 Beam model이 보 요소 자체의 유연성(Flexibility)으로 인해 스테빌라이저 바의 비틀림과 굽힘 현상을 잘 반영함을 알 수 있다.
3. 차량 동역학 해석
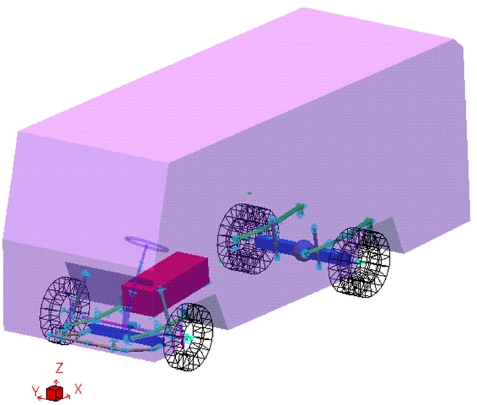
본 논문의 해석 대상 차량의 전후륜 현가장치는 판 스프링식 차축 현가장치이며, 조향계는 볼-너트 방식으로 기어비는 1:22.6이다. 조향계와 현가장치에 대한 기구학적 구속 조건을 부가하고, 스프링, 쇽업소버, 범프 스토퍼, 부싱 그리고 타이어 등과 같은 동특성 요소들을 적용하여 Fig. 10과 같은 전체 차량 모델을 구성하였다.
2.5절의 3가지 스테빌라이저 바 모델을 포함한 전체차량 모델의 자유도 수는 각각 Table 2에 나타내었다.
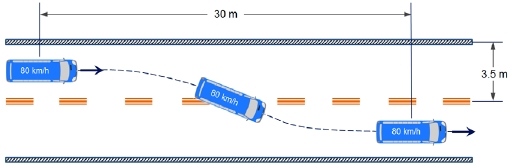
전체차량 모델의 동특성을 검토하기 위해 차선 변경 해석을 수행하였으며, 그와 동시에 실차 성능 시험도 병행하였다. 차선 변경 해석과 실차 성능 시험은 Fig. 11에서와 같이 80 km/h의 속도로 주행하던 중 길이 30 m, 폭 3.5 m인 도로 구간에서 3 초 동안 실시하였으며, 각 해석 모델의 해석 결과와 시험 결과를 비교 평가하였다.
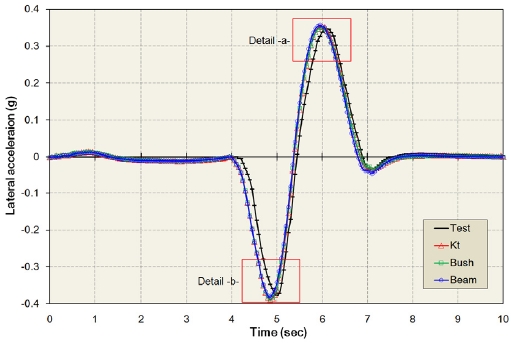
차선 변경 해석과 실차 시험의 평가 항목은 롤 각(Roll angel) θx, 롤 변화율(Roll rate) ωx, 요 변화율(Yaw rate) ωz 그리고 횡 가속도(Lateral acceleration) ay로써 차량의 조종 안정성을 평가하는 중요한 변수들이며, Fig. 12-23에 시간에 따른 각각의 변화 양상들을 도시하였다.
Figs. 12 ~ 23에 보이는 바와 같이 4가지 평가 항목들에 대해 각 해석 모델별로 절대값 측면에서는 시험 결과와 어느 정도의 차이를 보이지만, 변화 양상 및 감쇠 측면에 있어서는 시험 결과와 유사한 파형을 나타내었다. 따라서 3가지 전체차량 모델의 신뢰도는 확보된 것으로 판단할 수 있었다.
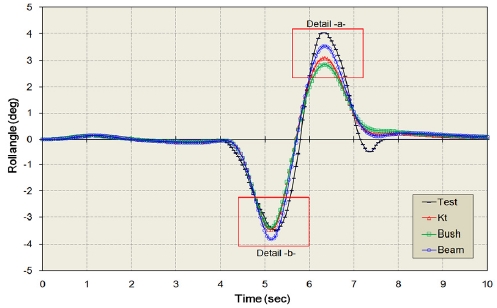
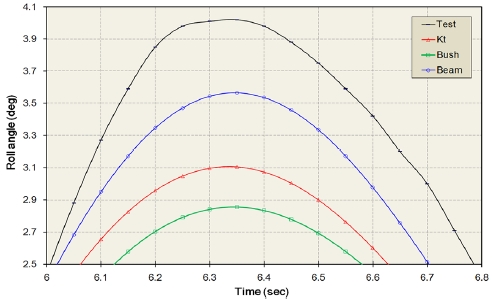
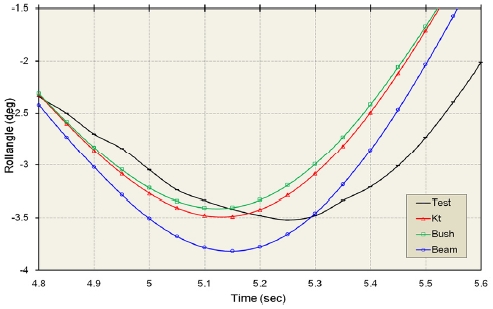
3.1 롤 각(Roll angle, θx)
Figs. 14 ~ 15는 차선 변경중에 차체의 최대 롤 각이 발생하는 시간에서의 롤 각의 변화를 나타낸다.
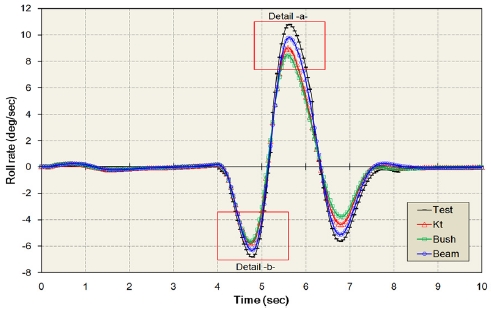
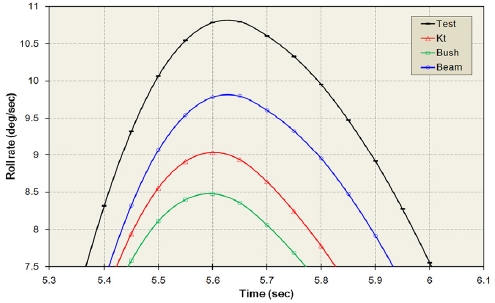
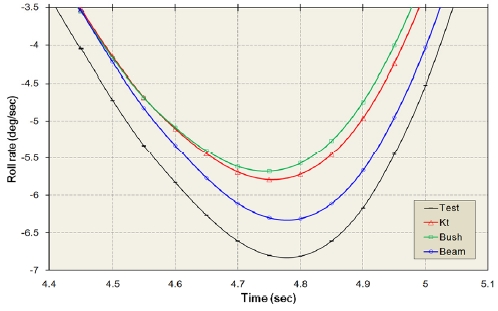
3.2 롤 변화율(Roll rate, ωx )
Figs. 16 ~ 17은 차선 변경중에 차체의 최대 롤 변화율이 발생하는 시간에서의 롤 변화율의 변화를 나타낸다.
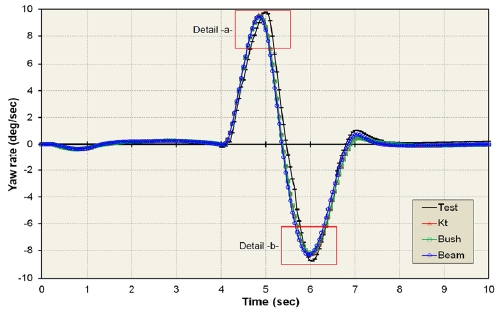
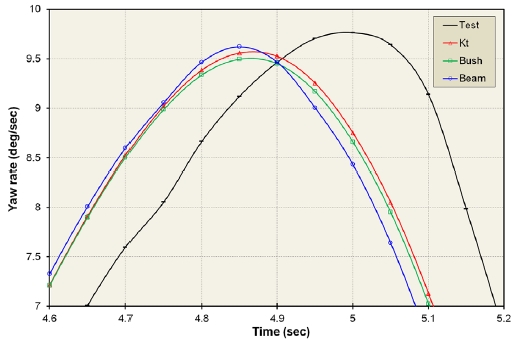
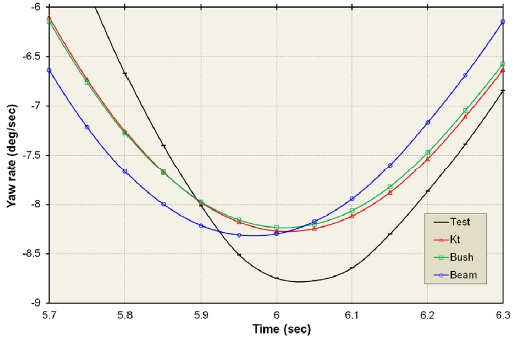
3.3 요 변화율(Yaw rate, ωz )
Figs. 19 ~ 20은 차선 변경중에 차체의 최대 요 변화율이 발생하는 시간에서의 요 변화율의 변화를 나타낸다.
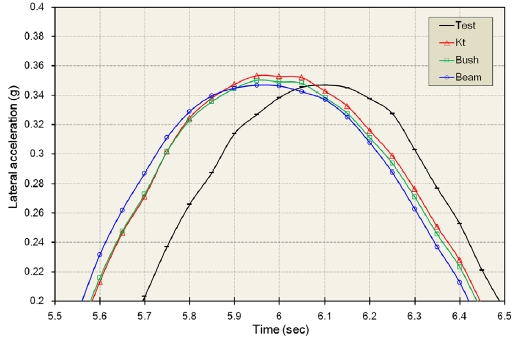
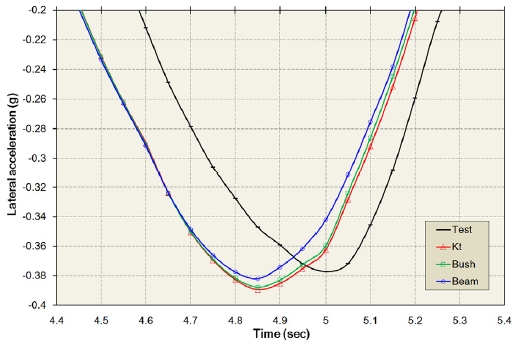
3.4 횡 가속도(Lateral acceleration, ay)
Figs. 22 ~ 23은 차선 변경 중에 차체의 최대 횡 가속도가 발생하는 시간에서의 횡 가속도의 변화를 나타낸다.
Table 3에 차선 변경 해석과 실차 시험 결과를 정량적으로 분석하기 위한 4가지 평가 항목들의 Peak-to-peak 값들을 정리하였다. 여기서, Peak-to-peak 값은 Figs. 12 ~ 23으로부터 구한 최대 값과 최저 값을 합한 값이다.
일반적으로 전후 강성비의 차이가 미미한 승용차의 경우는 차체를 강체로 모델링 하여도 해석 결과에 큰 영향을 주진 않지만, 중대형 버스나 트럭의 경우는 전후 강성 차이가 대략 5배 정도 이상이기 때문에 프레임을 강체로 모델링 하는 경우, 롤 강성이 해석 결과에 큰 영향을 미칠 수 있다. 이러한 요인으로 3가지 해석 모델에 대한 롤 각 및 롤 변화율의 해석 결과는 요 변화율이나 횡 가속도의 결과에 비하여 시험 결과와의 오차가 전반적으로 큼을 알 수 있다.
또한, 단일 차선 변경 시험을 수행하는 경우 프레임의 유연성(Flexibility)이 요 변화율과 횡 가속도 보다는 롤 운동에 좀 더 많은 영향을 줌을 알 수 있다.
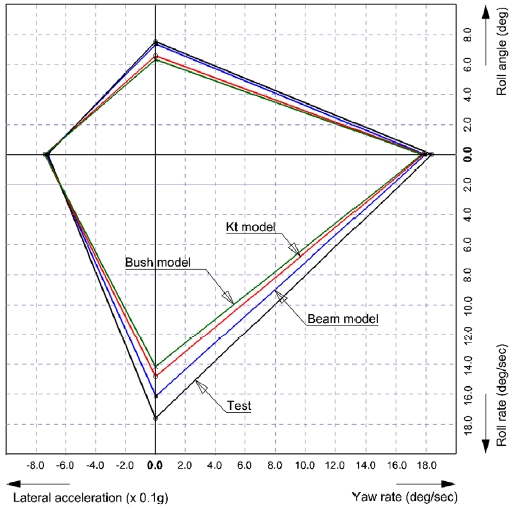
Beam model의 해석 결과들은 Kt model과 Bushing model에 비해 4가지 조종 안정성 평가 항목 모두 시험 결과에 거의 근접한 경향을 보였다. 이는 Beam model이 스테빌라이저 바의 비틀림과 굽힘 효과를 동시에 고려한 이유라 할 수 있다. 따라서 스테빌라이저 바의 비틀림과 굽힘을 가장 정확하게 반영하는 모델링 방법은 고유 형상과 힘 전달 경로를 고려한 유효 개수의 보 요소 모델링 방법임을 해석적으로 입증할 수 있었다.
Fig. 24는 3가지 해석 모델에 대한 시험 결과와의 비교 도표이다. 여기서 볼 수 있듯이, 4가지 평가 항목 모두에서 Beam model이 Kt model 및 Bush model과 비교할 때, 실차 시험결과와 가장 근접함을 알 수 있다. 이에 따라 Beam model의 모델링 방법의 유효성 및 신뢰성을 확보 할 수 있다.
4. 결 론
본 논문에서는 차량의 동특성인 조종 안정성에 대한 스테빌라이저 바 역할의 중요성에 대하여 서술하였으며, 스테빌라이저 바의 유한요소 모델링에 대한 롤 강성을 효과적으로 모델링하기 위하여 최적화된 유한요소 모델링 기법을 도출하였다. 그리고 이들 모델링 방법의 신뢰성을 검증하기 위한 시험 및 해석을 통해 다음과 같은 결론을 얻었다.
- 1) 보 요소를 이용하여 스테빌라이저 바를 모델링하는 경우, 단품의 고유 형상과 힘 전달 경로를 고려하여 즉, 프레임 마운팅 위치와 비틀림 중심에 절점을 생성하여 모델링하면 스테빌라이저 바 고유의 롤 강성을 유효하게 구현할 수 있다.
- 2) 현가 기구 해석에 적용될 스테빌라이저 바의 모델로는 Kt model, Bushing model 그리고 Beam model을 이용하였는데, 이 중 Beam model이 보 요소 고유의 유연성으로 인해 스테빌라이저 바의 비틀림과 굽힘 현상을 잘 반영하였다.
- 3) 차선 변경 해석을 통해 Beam model은 롤 각, 롤 변화율, 요 변화율 그리고 횡 가속도의 4가지 평가 항목에서 모두 시험 결과에 근접한 경향을 보였다.
- 4) 본 논문에 적용된 스테빌라이저 바의 보 요소 모델링 방법은 그 해석의 타당성과 신뢰성으로 인해 다른 새시 부품들에도 적용 가능함과 동시에 시작차 제작 이전에 차량의 조종 안정성을 예측하는데 있어 효과적일 것으로 판단된다.
References
- I. D. Moon, H. J. Kwon and C. Y. Oh, “Development of a Computer Model for the Turning Maneuver Analysis of a Heavy Truck,” Transactions of KSAE, Vol.8, No.4, pp.121-129, 2000.
- B. K. Cho and S. J. Song, “Modeling of Stabilizer for Vehicle Dynamic Analysis,” Journal of the Korean Society for Precision Engineering, Vol.13, No.10, pp.30-35, 1996.
- K. S. Kim, H. M. Kil and W. S. Yoo, “Development of a CAE Technique for Vehicle Suspension Design,” Journal of the Korean Society for Precision Engineering, Vol.15, No.1, pp.160-168, 1998.
- Spring Design Manual, SAE International, 1990.
- ADAMS/SOLVER Reference Manual, Mechanical Dyanamics Inc., 1994.