주파수와 진폭에 따른 비선형 동특성 예측을 위한 현가장치 부시 모델에 대한 연구

1. 서 론

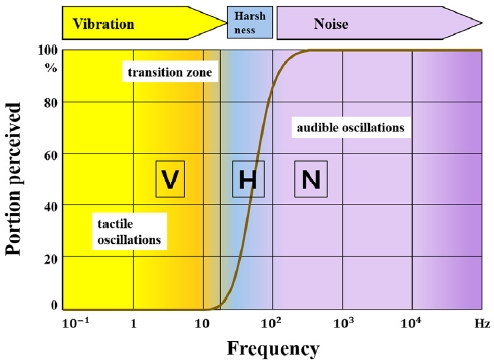
현가장치는 차량의 승차감 및 핸들링(R&H: Ride and Handling), 내구, 소음 및 진동(NVH: Noise, vibration and harshness) 등의 다분야 성능에 영향을 주는 시스템이다. 이와 같은 차량의 다분야 성능 향상을 위해서는 현가장치의 동특성에 대한 정확한 예측이 필요하다. 하지만 현가장치의 심한 비선형성으로 인해 동특성을 정확히 예측하기란 쉽지 않다. 특히, 부시는 높은 비선형 동특성을 가진 부품 중 하나로 현가장치의 동특성에 미치는 영향이 크다. Fig. 1과 Table 1은 차량의 소음(Noise), 진동(Vibration), 충격에 의한 소음 및 진동(Harshness) 현상에 대해 각각의 주파수 범위를 보여준다.¹⁾

Fig. 1

Oscillation frequency ranges associated with the terms noise, vibration, and harshness

Table 1

Frequency range of oscillatory phenomena

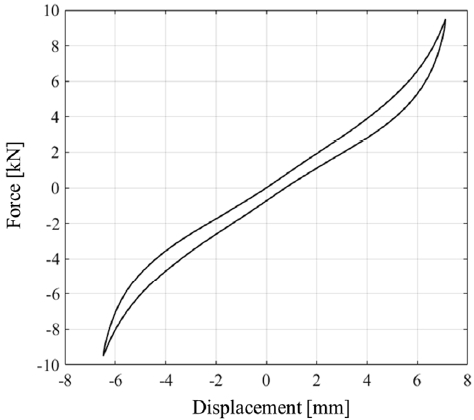
소음의 경우 약 100 Hz 이상의 주파수 범위를 보이며, Table 1의 구동계 소음(Powertrain noise)은 1000 Hz까지의 높은 주파수까지도 작용한다. 또한, 부시는 Fig. 2의 힘-변위 선도에서 볼 수 있듯이 마찰로 인한 이력 현상(Hysteresis)을 동반한다.

Fig. 2

Hysteresis of the suspension bush in quasi-static test

이러한 이력 현상은 높은 가진 진폭을 다루는 내구 성능에 영향을 준다. 반면, 차량 동역학(Vehicle dynamics) 소프트웨어에 일반적으로 사용되는 부시 모델은 켈빈-포크트(Kelvin-Voigt) 모델로 비선형 스프링과 댐퍼 요소가 병렬로 연결된 형태이다. 이 모델은 부시의 주파수와 진폭에 따른 동특성 변화를 표현하지 못한다. 따라서, 앞서 설명한 고주파수 영역을 다루는 소음 및 진동 분야 혹은 높은 진폭을 다루는 내구 분야의 성능 예측에는 별도의 고정도 부시 모델이 필요하다. 이를 위해 부시의 주파수와 진폭에 따른 비선형 동특성을 표현하기 위한 모델링 기법들이 연구되었다.

먼저, 비선형 이력 현상을 표현하기 위한 방법으로 Bouc-Wen 모델을 활용한 부시 모델링 기법이 많이 연구되었다.^2-4) Bouc-Wen 모델은 부시의 이력 현상을 잘 표현하므로 진폭에 따른 동특성을 매우 잘 표현할 수 있다. 일반적으로 Bouc-Wen 모델과 주파수에 따른 동특성을 표현하기 위한 댐퍼 요소를 결합하여 사용되었다. 하지만 Bouc_Wen 모델의 동강성(Dynamic stiffness)과 위상각(Phase angle)을 계산하기 위해서는 미분방정식을 직접 풀어야 하므로 모델의 파라미터를 찾는 과정에서 시간이 많이 소요된다. 신경망(Neural network)을 이용한 부시 모델링 기법도 연구되었다.^5-7) 신경망 모델의 경우 많은 학습 데이터를 필요로 하며, 부시의 동특성에 대해 모델의 파리미터가 갖는 의미가 모호하여 설계 시 사용하기 어렵다는 단점이 있다. 이러한 문제점들을 해결하기 위해 스프링과 댐퍼 요소의 단순 조합을 통해 만들어진 일반화된 맥스웰 모델(Generalized Maxwell model)과 마찰 맥스웰 모델(Frictional Maxwell model)을 활용한 부시 모델링 기법이 연구되었다.^8,9) 맥스웰 모델은 동적 강성과 위상 지연을 주파수와 진폭에 대한 함수로 나타낼 수 있기 때문에 모델의 파라미터를 찾는 과정이 비교적 간단하다는 장점이 있다. 그리고 스프링, 댐퍼 및 마찰 상수는 부시의 동특성에 주는 영향이 직관적이기 때문에 설계 시에도 유리하다.

기존 연구들에서는 주로 부시 단품 단위에서의 동특성 예측을 다루었다. 따라서, 부시의 시스템 단위에서의 동특성 예측 정확도에 대한 연구가 미흡하다. 본 논문에서는 다물체 동역학(Multibody dynamics) 해석에 사용할 수 있고 주파수와 진폭에 따른 비선형 동특성을 고려할 수 있는 부시를 모델링 하고, 이를 현가 장치 동역학 모델에 적용하여 시스템 단위에서의 동특성 예측 정확도에 대해 검증한다. 모델의 형태는 일반화된 맥스웰 모델과 마찰 맥스웰 모델이 결합된 형태를 사용한다. 이 때, 동역학 해석의 효율을 위해 스무딩(Smoothing)된 마찰 모델을 사용한다. 본 논문에서 다루는 주파수 범위는 300 Hz까지로 Table 1의 구동계 소음을 제외한 나머지 성능들을 부시 모델의 적용 범위로 한다. 2 장에서는 비선형 동특성 부시 모델의 구조를 소개하고 제안된 부시 모델의 파라미터 최적화 프로세스를 정립한다. 3 장에서는 적용 사례로 전륜 맥퍼슨 현가장치의 부시들의 모델 파라미터를 최적화하고 그 결과를 확인한다. 그리고 전륜 맥퍼슨 현가장치에 대해 Half-car 내구 시뮬레이션을 진행하여 제안된 부시 모델과 기존의 켈빈-포크트 부시 모델의 동특성 예측 정확도를 현가 시스템 단위에서 비교한다.

2. 비선형 동특성 부시 모델링

2.1 모델링 방법

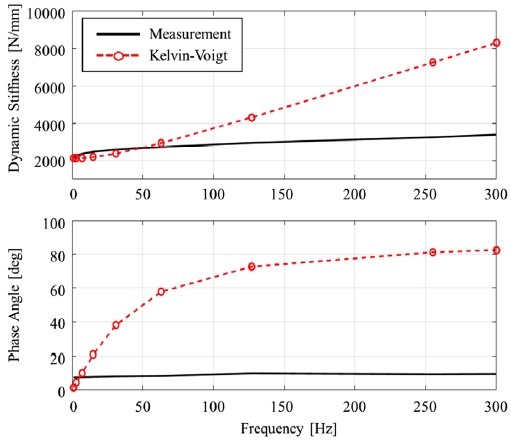
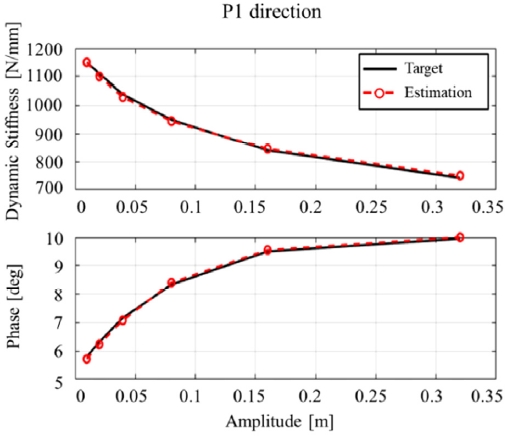
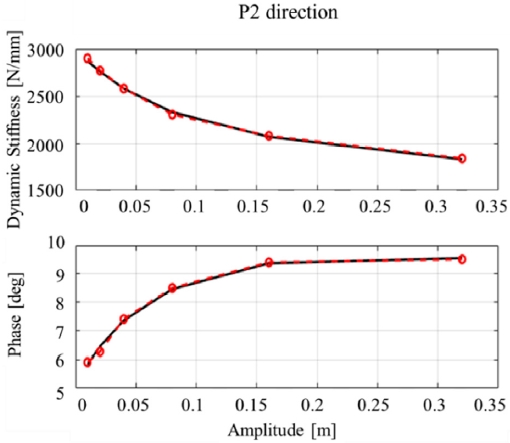
일반적으로 현가장치 부시는 Fig. 3과 같이 주파수와 진폭에 따라 동강성과 위상각이 비선형적으로 변화한다. 그림에서 볼 수 있듯이 켈빈-포크트 모델로는 이러한 부시의 비선형 동특성을 표현하지 못한다.

Fig. 3

Nonlinear dynamic characteristic of suspension bush

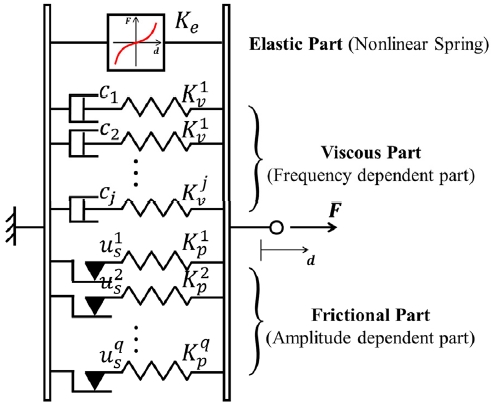
따라서 본 논문에서는 이러한 주파수와 진폭에 따른 부시의 동특성 변화를 표현하기 위해 Fig. 4의 모델 형태를 사용한다. 모델은 탄성 부분(Elastic part), 점성 부분(Viscous part), 마찰 부분(Frictional part)로 나뉜다. 여기서, 탄성 부분과 점성 부분이 결합된 형태가 기존의 일반화된 맥스웰 모델이다. 탄성 부분은 부시의 정적 강성을 나타낸다. 점성 부분은 부시의 주파수에 따른 동특성 변화를 표현하는 역할을 한다. 그리고 마찰 부분은 진폭에 따른 동특성 변화를 표현하는 역할을 한다.

Fig. 4

Nonlinear dynamic bush model

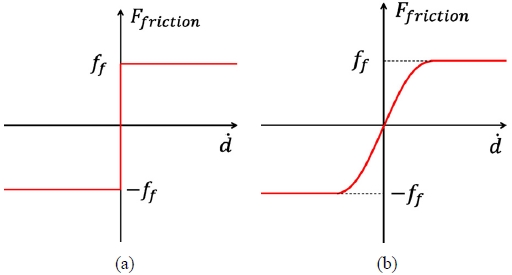
마찰 부분에서 일반적으로 사용되는 마찰 모델의 경우 식 (1)과 Fig. 5(a)에서 볼 수 있듯이 속도가 0인 지점에서 불연속점이 존재한다. 이러한 마찰 모델을 사용할 경우 다물체 동역학 해석 시 수렴성이 낮고 해석시간이 높아진다는 단점이 있다. 이를 위해 본 논문에서는 식 (2)와 Fig. 5(b)의 쌍곡탄젠트(Hyperbolic tangent) 함수 기반 마찰 모델을 사용하여 모든 점에서 연속이 되도록 한다.

Fig. 5

General friction models

$\[ F_{friction}=f_f\text{sign}\left(\dot{d}\right) \]$

(1)

$\[ F_{friction}=f_f\text{sign}\left(\alpha \dot{d}\right) \]$

(2)

마지막으로 앞서 설명한 비선형 동특성 힘요소 모델을 병진 3 방향, 회전 3 방향의 총 6 자유도로 결합하여 부시 모델을 구성한다.

2.2 부시 모델 파라미터 최적화 프로세스

부시 모델의 파라미터를 최적화하기 위해서는 해당 부시의 정적 시험(Static test)과 동적 시험(Dynamic test) 데이터가 필요하다. 정적 시험은 비선형 동특성 부시 모델의 탄성 부분의 강성 데이터를 도출하기 위한 시험이다. 그리고 동적 시험은 주파수 변화 시험(Frequency sweep test)과 진폭 변화 시험(Amplitude sweep test)으로 나뉘며 각 조건에서의 동강성과 위상각을 도출한다. 본 논문에서 진행한 시험의 조건은 Table 2와 같다. 정적 강성 시험의 경우 부시와 측정 방향에 따라 진폭 범위가 상이하며 기재된 값은 최대 범위를 의미한다. 본 논문에서는 부시의 병진 3 자유도에 대해서 시험과 모델링을 진행했다.

Table 2

Bush static and dynamic test

시험을 완료한 후에는 탄성 부분에 사용할 힘-변위 데이터를 도출하기 위해 정적 시험 데이터를 식 (3)의 5차 함수로 곡선 접합(Curve fitting)한다.

$\[ F_e=a_0+a_1\mathit{d}+a_2{\mathit{d}}^2+a_3{\mathit{d}}^3+a_4{\mathit{d}}^4+a_5{\mathit{d}}^5 \]$

(3)

그리고 점성 부분과 마찰 부분의 경우 비선형 동특성 부시 모델을 같은 조건으로 해석 시 도출된 동강성과 위상각이 시험 데이터와 같은 값을 낼 수 있도록 파라미터를 최적화해야 한다. 이를 위해선 비선형 동특성 부시 모델의 동강성과 위상각을 계산해야 한다. 맥스웰 모델의 동강성과 위상각은 식 (4), (5)와 같다. 탄성 부분과 맥스웰 모델 n개가 병렬로 연결된 형태인 일반화된 맥스웰 모델의 동강성과 위상각은 식 (6), (7)이 된다. 여기서, 탄성 부분의 강성 K_e는 식 (3)에 해당 시험의 변위를 입력하여 구한 하중의 피크 대 피크(Peak to peak)값을 변위의 피크 대 피크 값으로 나눈 값이다.

$\[ K_{dyn}^{v,j}=K_v^j\frac{{\omega }^2{t}_{r,j}^2}{1+{\omega }^2{t}_{r,j}^2} \]$

(4)

$\[ \sin \left({\delta }_v^j\right)=\frac{1}{\sqrt{1+{\omega }^2{t}_{r,j}^2}} \]$

(5)

$\[ \begin{array}{c}\sin \left({\delta }_v^j\right)=\frac{1}{\sqrt{1+{\omega }^2{t}_{r,j}^2}}\hfill \\ =\sqrt{{\left(K_e+\sum _{j=1}^n{K}_{dyn}^{v,j}\cos \left({\delta }_v^j\right)\right)}^2+{\left(\sum _{j=1}^n{K}_{dyn}^{v,j}\sin \left({\delta }_v^j\right)\right)}^2}\hfill \end{array} \]$

(6)

$\[ \sin \left({\delta }_v\right)=\frac{1}{K_{dyn}^v}\sum _{j=1}^n\frac{K_{dyn}^{v,j}}{\sqrt{1+{\omega }^2{t}_{r,j}^2}} \]$

(7)

마찰 맥스웰 모델의 동강성과 위상각은 식 (8), (9)이며, 마찰 맥스웰 모델 개가 병렬로 연결된 마찰 부분의 총 동강성과 위상각은 식 (10), (11)과 같다.

(8)

(9)

$\[ K_{dyn}^p=\sum _{q=1}^m{K}_{dyn}^{p,q} \]$

(10)

$\[ \sin \left({\delta }_p\right)=\frac{{\sum }_{q=1}^m{U}_s^q}{\pi \widehat{u}{\sum }_{q=1}^m{K}_p^q{u}_s^q} \]$

(11)

이를 기반으로 Fig. 4 모델의 전체 동강성과 위상각은 식 (12)과 (13)으로 근사화될 수 있다.⁸⁾

$\[ K_{dyn}\approx K_{dyn}^v\left(\omega \right)+K_{dyn}^p\left(\widehat{u}\right) \]$

(12)

$\[ \sin \left(\delta \right)\approx \frac{K_{dyn}^v\left(\omega \right)\sin \left({\delta }_v\right)+K_{dyn}^p\left(\widehat{u}\right)\sin \left({\delta }_p\right)}{K_{dyn}} \]$

(13)

위의 식들은 모두 진폭과 주파수에 대한 함수이기 때문에 미분방정식을 풀지 않아도 동강성과 위상각을 계산할 수 있다. 계산된 동강성 및 위상각과 계측 데이터와의 오차를 통해 식 (14)와 같은 벌칙 함수(Cost function)를 구성한다. 시뮬레이션 값을 시험 값으로 나눈 후 1을 뺀 형태를 활용하여 동강성과 위상각의 오차값을 정규화(Normalization) 한다.

$\[ J=\sum _{i=1}^n\left(k{\left(\frac{K_{dyn,sim}^i}{K_{dyn,test}^i}-1\right)}^2+\left(1-k\right){\left(\frac{{\delta }_{sim}^i}{{\delta }_{test}^i}-1\right)}^2\right) \]$

(14)

구성된 벌칙 함수를 최소화하는 최적화 문제를 풀기 위해 순차적 2차 계획법(SQP: Sequential quadratic progra-mming)을 활용하였다. 순차적 2차 계획법은 비선형 최적화(Nonlinear optimization)에 대표적으로 사용되는 반복 처리 방법(Iterative method)으로 부시와 같은 비선형성이 높은 시스템에 대해 적합한 방법이다. 설계 변수(Design variable)는 점성 부분의 강성들과 댐핑 계수들, 마찰 부분의 강성들과 마찰 변위 임계값들이다.

3. 비선형 동특성 부시 다물체 동역학 해석

3.1 부시 모델 파라미터 최적화

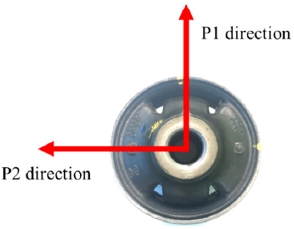
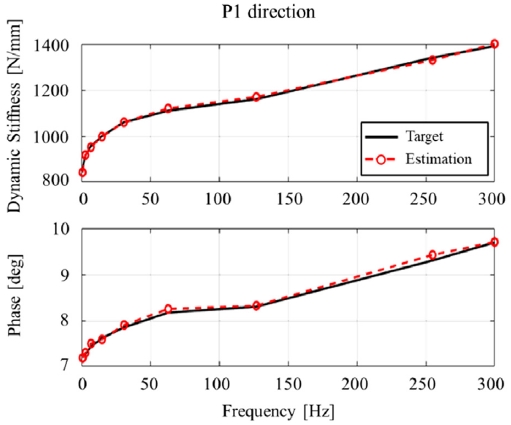
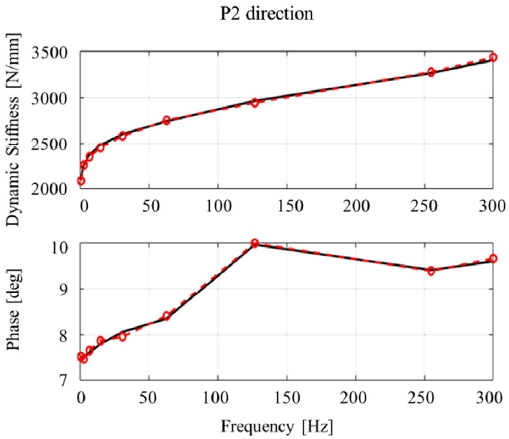
이번 장에서는 2 장에서 제안한 모델링 방법을 전륜 맥퍼슨 현가장치의 보이드 부시(Void bush)에 적용한다. 계측 방향은 Fig. 6의 P1과 P2 방향이다. 점성 부분에는 3 개의 맥스웰 모델, 마찰 부분에는 3 개의 마찰 맥스웰 모델을 사용하였다. Table 3과 Table 4는 최적화된 파라미터 값을 보여준다. Fig. 7과 Fig. 8은 주파수 변화 시험에 대한 예측 결과이며, Fig. 9와 Fig. 10은 진폭 변화 시험에 대한 예측 결과이다.

Fig. 6

Bush of Mcpherson suspension

Table 3

Parameters of nonlinear dynamic bush model (P1)

Table 4

Parameters of nonlinear dynamic bush model (P2)

Fig. 7

Results of frequency sweep test (P1)

Fig. 8

Results of frequency sweep test (P2)

Fig. 9

Results of amplitude sweep test (P1)

Fig. 10

Results of amplitude sweep test (P2)

Table 5에서 볼 수 있듯이 동적 시험에서 동강성과 위상각의 평균 제곱근 오차율은 각각 3 %, 4 % 이내로 높은 예측 정확도를 보였다. 이는 본 논문에서 제안한 부시 모델이 부시의 비선형 동특성을 잘 나타낼 수 있음을 입증한다.

Table 5

Root mean square error of nonlinear dynamic bush model

3.2 현가장치 시스템 특성 예측

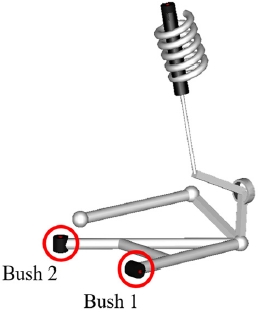
비선형 동특성 부시 모델의 목표인 현가장치 시스템 특성 예측 정확도를 평가하기 위해 본 논문의 방법론으로 모델링한 부시들을 다물체 동역학 기반 전륜 맥퍼슨 현가장치 모델에 적용하여 Half-car 내구 시뮬레이션을 진행한다. 소프트웨어는 Dymola(Dassault Systèmes, France)를 사용했다. 해당 부시는 Fig. 11에 표시한 Bush 1, Bush 2이며, 3 자유도 병진 방향에 대해 본 논문의 모델링 방법을 적용하였다.

Fig. 11

Results of frequency sweep test

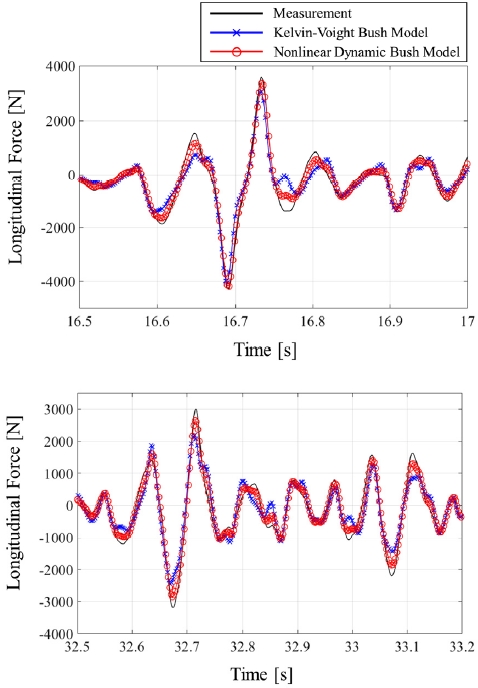
Half-car 내구 시뮬레이션의 구동 신호(Drive signal)로는 가속 내구로 중 하나인 벨지안 로(Belgian road) 주행 시험에서 계측된 6 분력 휠하중을 사용한다. 차량 주행 시험에서 부시의 하중을 직접 측정하기 어렵다. 또한, 두 부시가 모두 작용한 시스템 특성을 확인하기 위해 본 논문에서 다룰 출력 신호로 직접 계측이 가능한 볼조인트의 종횡방향 하중을 선정했다. 비선형 동특성 부시 모델을 적용한 시뮬레이션 결과는 계측 신호 및 기존에 부시 모델로 사용되던 켈빈-포크트 부시 모델의 시뮬레이션 결과와 비교한다.

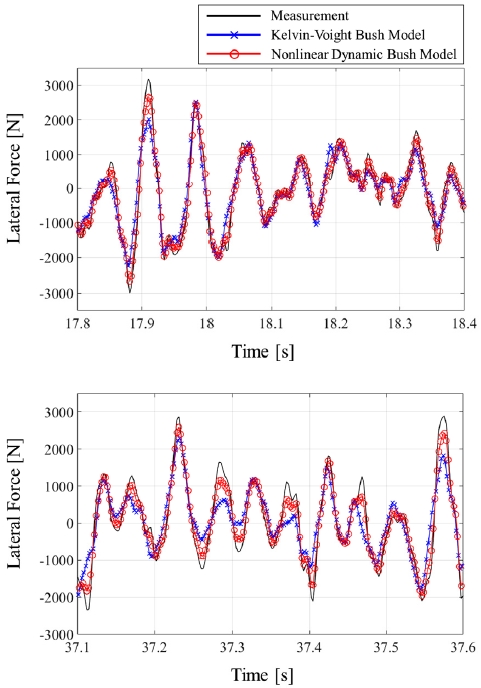
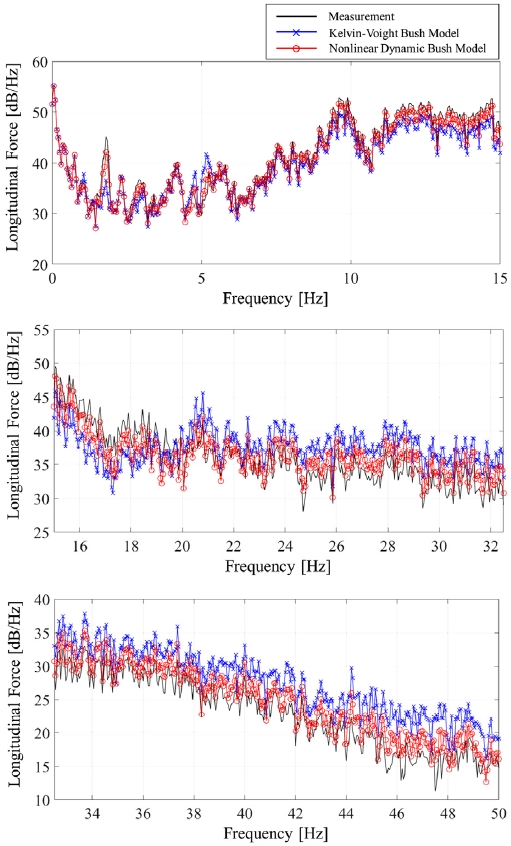
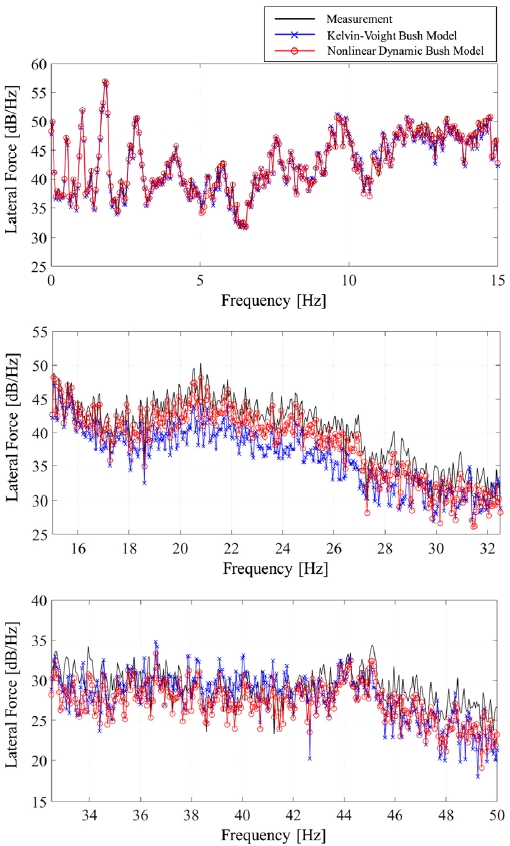
Fig. 12와 Fig. 13의 하중 시간 선도의 일부분들을 보면 켈빈-포크트 부시 모델에 비해 비선형 동특성 부시 모델의 결과가 계측 신호와 더 적은 오차를 보임을 알 수 있다. Fig. 14와 Fig. 15의 에너지 스펙트럼 밀도(PSD: Power spectral density) 선도와 Table 6을 통해서는 저주파수 영역인 약 15 Hz 미만의 영역에서는 켈빈-포크트 부시 모델과 비선형 동특성 부시 모델의 정확도가 유사하다는 것을 알 수 있다. 하지만 그 이상의 영역에서는 켈빈-포크트 부시 모델의 정확도가 감소하는 것을 볼 수 있다.

Fig. 12

Longitudinal force of ball joint (time history)

Fig. 13

Lateral force of ball joint (time history)

Fig. 14

Longitudinal force of ball joint (power spectral density)

Fig. 15

Lateral force of ball joint (power spectral density)

Table 6

Root mean square error of nonlinear dynamic bush model

켈빈-포크트 부시 모델은 2.1절의 Fig. 3에서 확인할 수 있듯이 약 10~15 Hz 이상의 가진 주파수 영역에서 주파수가 증가할수록 실제 부시의 동특성과의 오차가 증가한다는 것을 알 수 있다. 이러한 켈빈-포크트 부시 모델의 특징은 고주파수 영역에서의 시스템 단위에서도 영향을 끼쳐 시스템 특성 예측 정확도를 감소시켰음을 알 수 있다. 반면, 본 논문에서 제안한 비선형 동특성 부시 모델은 3.1절에서도 확인했듯이 300 Hz까지의 부시 동특성을 비교적 높은 정확도로 예측하였다. 이는 부시 단위의 높은 동특성 예측 정확도가 시스템 단위의 고주파수 영역 특성 예측에도 효과가 있음을 의미한다.

4. 결 론

본 논문에서는 부시의 주파수 및 진폭에 따른 동특성 변화를 구현하기 위한 비선형 동특성 부시를 모델링하고 이에 대한 현가 시스템 단위에서의 정확도를 평가하였다. 모델은 탄성 부분, 점성 부분, 마찰 부분이 병렬 연결된 형태를 사용했다. 탄성 부분과 점성 부분은 일반화된 맥스웰 모델을 사용하고 마찰 부분은 마찰 맥스웰 모델을 사용하였다. 경사하강법 알고리즘을 기반으로 부시 모델의 파라미터 최적화 과정을 정립하고 이를 후륜 멀티링크 타입 현가장치의 어시스트 링크 부시에 적용하였다. 그리고 다물체 동역학 현가장치 모델에 이 부시 모델을 적용하여 half-car 내구 시뮬레이션을 진행했다. 그 결과는 다음과 같다.

부시 모델의 파라미터를 최적화한 결과, 동강성과 위상각에 대한 계측 데이터와의 평균 제곱근 오차가 3 %, 4 % 이내로 높은 동특성 예측 정확도를 보였다.

Half-car 내구 시뮬레인션은 기존에 사용되던 켈빈-포크트 부시 모델보다 비선형 동특성 부시 모델이 부품 하중의 이력 현상에 대한 예측 정확도가 높았다.

Half-car 내구 시뮬레이션의 주파수 영역 특성에서 켈빈-포크트 부시 모델에 비해 비선형 동특성 부시 모델이 저주파수와 고주파수 영역 모두에서 더 높은 정확도를 보였다.

이러한 결과를 통해 본 논문에서 제안한 비선형 동특성 부시 모델이 부품 단위에서의 동특성 뿐만 아니라 시스템 단위에서의 부품의 동특성 예측에 대해서도 효과가 있음을 입증했다. 향후에는 본 논문에서 다루지 못한 비선형 동특성 부시 모델의 맥스웰 및 마찰 맥스웰 모델 개수에 대한 최적화와 소음 및 진동 해석을 추가로 진행하여 범용성을 높일 것이다. 또한, 차량 시스템 단위로 범위를 확장하여 부시 모델의 동특성 예측 정확도 검증을 진행할 것이다.

References

• B. Heißing and M. Ersoy, Chassis Handbook, 1st Edn., Springer Fachmedien Wiesbaden GmbH, Wiesbaden, 2011.
• J. Ok, W. Yoo and J. Sohn, “Development of Uni-Axial Bushing Model for the Vehicle Dynamic Analysis Using the Bouc-Wen Hysteretic Model,” Transactions of KSAE, Vol.14, No.2, pp.158-165, 2006.
• J. Ok, D. Park, W. Yoo and J. Sohn, “Development of a New Bushing Model for Vehicle Suspension Module Design,” Transactions of KSAE, Vol.14, No.6, pp.143-150, 2006.
• J. Ok, W. Yoo and J. Sohn, “New Nonlinear Bushing Model for General Excitations Using Bouc-Wen hysteretic Model,” Int. J. Automotive Technology, Vol.9, No.2, pp.183-190, 2008. [https://doi.org/10.1007/s12239-008-0023-8]
• J. Sohn, W. Yoo and D. Park, “Empirical Bushing Model using Artificial Neural Network,” Transactions of KSAE, Vol.11, No.4, pp.151-157, 2003.
• J. Sohn, T. Kang and W. Baek, “Vehicle Dynamic Simulation Using the Neural Network Bushing Model,” Transactions of KSAE, Vol.12, No.4, pp.110-118, 2004.
• S. Lee, K. Kim and J. Sohn, “Optimization of Neural Network Structure for the Efficient Bushing Model,” Transactions of KSAE, Vol.15, No.5, pp.48-55, 2007.
• F. Karlsson and A. Persson, Modelling Non-linear Dynamics of Rubber Bushings-parameter Identification and Validation, M. S. Thesis, Lund University, Lund, 2005.
• S. Park, Y. Jeon, D. Kang, M. Hyun and S. Heo, “Predicting the Vehicle Performance at an Early Stage of Development Process via Suspension Bushing Design Tool,” Proceedings of the 13th International Modelica Conference, pp.819-826, 2019. [https://doi.org/10.3384/ecp19157819]