핸들링 및 조타감의 주관/객관 성능 간 상관 관계 모델링 방법에 대한 연구
Copyright Ⓒ 2020 KSAE / 178-01
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
In this paper, we study the correlation modeling method between subjective assessments and objective metrics of handling and steering feel. The correlation model used is a multiple linear regression model. To resolve multicollinearity that can cause overfitting, we use ridge regression, which is a normalization method. Interaction terms between independent variables are also added to the multiple linear regression model so that correlations between objective metrics can be considered. As an application of the proposed method, correlation modeling between subjective assessments and objective metrics of handling and steering feel is performed. To evaluate the accuracy of the proposed model, we compare it with a multiple linear regression model based on the least square method and a ridge regression model without interaction term. Results show the ridge regression with interaction terms has the highest accuracy in terms of coefficient of determination and mean square error.
Keywords:
Subjective assessment, Objective metrics, Correlation model, Multiple linear regression, Ridge regression, Interaction키워드:
주관적 평가 항목, 객관적 측정 항목, 상관 관계 모델, 다중 선형 회귀, 능형 회귀, 교호작용1. 서 론
차량 개발 단계에서 목표 성능은 기본적으로 해당 시장의 고객 요구 사항(Customer requirements)을 기반으로 결정된다. 이 때, 고객 요구 사항과 차량의 성능 지수들 간의 연결성이 파악되어야 차량의 목표 성능 지수를 올바르게 설정하여 설계를 진행할 수 있다. 하지만 고객의 요구 사항이 핸들링 감성 및 조타감과 같은 주관적 평가 항목(Subjective assessments)인 경우 객관적 측정 항목(Objective metrics)인 차량의 성능 지수와의 연결성을 파악하기 어렵다. 이를 위해 주관/객관 성능 간 상관 관계 분석(Correlation analysis)에 대한 연구들이 진행되었다.1-3) 상관 관계 분석 방법으로 주로 사용된 방법은 최소 자승법(LSM: Least square method) 기반의 선형 회귀(Linear regression)이다. 먼저, 선형 회귀 방법 중 하나인 단순 선형 회귀(Simple linear regression)를 통해 주관적 평가 항목과 객관적 측정 항목 간의 일대일 상관 관계를 분석하는 연구가 진행되었다.4-6) 하지만 주관적 평가 항목 점수에는 여러 객관적 측정 항목들이 복합적으로 영향을 주기 때문에 단순 선형 회귀 모델로는 이들의 상관 관계를 정확히 파악하기에는 한계가 있었다. 이러한 한계점을 해결하기 위해 다중 선형 회귀(Multiple linear regression)를 이용한 상관 관계 분석 방법에 대한 연구가 진행되었다.7,8) 다중 선형 회귀 모델은 두 개 이상의 객관적 측정 항목으로 주관적 평가 항목을 예측하도록 하여 기존의 단순 선형 회귀 모델보다 정확도를 높일 수 있었다. 하지만 다중 회귀 모델은 독립변수 간에 높은 상관도가 존재할 경우 과적합(Overfitting)을 야기하는 다중공선성(Multicollinearity)이 발생할 수 있다. 특히, 차량의 동적 특성에 의해 결정되어지는 핸들링 혹은 조타감의 객관적 측정 항목들의 경우 서로 간의 상충 관계로 인해 높은 상관도를 가지는 경우가 많다. 이를 독립변수로 사용할 경우 다중공선성이 발생할 가능성이 더욱 크다. 이를 해결하기 위해 정규화 방법 중 하나인 능형 회귀(Ridge regression)를 활용하는 연구가 진행되었다.9,10) 능형 회귀는 다중공선성을 발생시키는 독립변수의 계수를 줄임으로써 과적합을 완화시키는 것이 가능하다. 하지만 정규화를 통해 신뢰도는 높아졌지만 모델의 전체적인 정확도가 감소하는 과소적합(Underfitting)이 발생하는 경우가 있다. 이러한 현상이 발생하는 이유 중 하나는 독립변수 간의 상관 관계가 종속변수에 끼치는 영향이 큰 경우 이를 제거하는 능형 회귀의 특징이 오히려 모델의 정확도를 감소시킬 수 있다는 점이다.
본 논문에서는 위의 문제점들을 해결할 수 있는 핸들링과 조타감의 주관/객관 성능 간 상관 관계 모델링 방법을 제안한다. 상관 관계 모델은 객관적 측정 항목 간의 상관 관계를 고려하기 위해 기존의 다중 선형 회귀 모델에 객관적 측정 항목들 간의 곱으로 이루어진 교호 작용(Interaction) 항을 추가한 형태를 사용한다. 이 모델의 계수는 기존 연구들에서 주로 사용되던 능형 회귀를 이용하여 계산한다. 먼저, 2 장에서는 능형 회귀와 교호 작용 항이 추가된 다중 회귀 모델에 대해 설명한다. 그리고 이들을 이용한 주관/객관 성능 간 상관 관계 모델링 프로세스를 설명한다. 3 장에서는 제안된 모델링 프로세스를 적용할 핸들링과 조타감의 주관적 평가 항목과 객관적 측정 항목들의 데이터 세트(Data set)를 정리한다. 4 장에서는 적용 사례의 데이터 세트에 대해 최소 자승법 기반의 다중 선형 회귀 모델, 교호 작용 항이 없는 능형 회귀 모델, 마지막으로 본 논문에서 제안한 교호 작용 항이 포함된 능형 회귀 모델을 각각 구축하여 정확도를 비교한다. 5 장에서는 4 장의 결과를 기반으로 모델들의 성능을 평가하고 제안된 모델에 선정된 핸들링 및 조타감 객관적 측정 항목들에 대한 분석을 진행한다.
2. 주관/객관 성능 간 상관 관계 모델링 방법
2.1 능형 회귀
차량의 핸들링 및 조타감에 대한 객관적 측정 항목들은 모두 차량의 동적 응답을 기반으로 만들어지기 때문에 서로 높은 상관도를 가지고 있는 경우가 많다. 이렇게 높은 상관도를 가지는 항목들을 다중 선형 회귀 모델의 독립 변수로 사용할 경우 다중공선성이 발생해 모델의 과적합을 야기시킨다. 이러한 다중공선성을 해결하기 위한 대표적인 방법은 능형 회귀(Ridge regression)이다. 일반적으로 다중 선형 회귀 모델인 식 (1)을 구축하기 위한 벌칙 함수(Cost function)로 식 (2)의 최소 자승법이 사용된다. 최소 자승법에 의해 추정되는 계수는 식 (3)으로 이상점(Outlier)을 포함한 y에 대해 매우 민감하기 때문에 과적합을 일으키는 계수를 추정할 가능성이 높다.
| (1) |
| (2) |
| (3) |
능형 회귀의 경우 식 (4)와 같이 식 (2)에 계수 제곱의 합으로 구성된 정규화 항(Regularization term)을 추가한 벌칙 함수를 사용한다. 이 정규화 항의 추가로 인해 추정되는 계수는 식 (5)가 되며, 정규화 상수 k는 특정 변수의 계수가 과도하게 커지는 것을 방지해주는 역할을 한다. 이를 통해 다중공선성이나 이상점에 의한 과적합을 완화시킬 수 있다. 본 논문에서는 정규화 상수 k의 값을 최적화하여 다중 선형 회귀 모델의 정확도 및 신뢰도를 향상시킨다.
| (4) |
| (5) |
2.2 교호 작용을 포함한 다중 회귀 모델
기본적인 다중 선형 회귀 모델은 식 (1)과 같이 각 독립변수에 계수가 곱해져 있는 항들의 합으로 이루어져 있다. 이는 각 독립변수가 서로 독립이라는 전제 하에서만 정확한 모델이 형성될 수 있다는 것을 뜻한다. 하지만 핸들링, 조타감과 같은 차량의 동특성을 기반으로 형성되는 성능들의 경우 각 성능 지수 간에 일련의 상관 관계가 존재한다. 따라서 이러한 성능 지수들을 독립 변수로 사용할 경우 앞서 설명한 다중공선성이 발생할 수 있다. 이러한 변수들 간의 관계로 인해 발생하는 작용을 교호 작용이라 한다. 앞서 설명한 능형 회귀를 통해 다중공선성을 일으키는 변수의 계수 값을 줄여 과적합을 예방할 수는 있다. 하지만 독립 변수들 간의 교호 작용이 모델에 끼치는 영향이 매우 큰 경우 이에 대한 영향을 인위적으로 줄였을 때 모델의 정확도가 오히려 떨어지는 과소적합(Underfitting)이 일어날 가능성이 있다.
본 논문에서는 이를 해결하기 위해 상관 관계 모델로 기존의 다중 선형 회귀 모델의 독립 변수들 간 곱의 항을 추가하여 교호 작용을 고려한다. 기존 모델에 사용되는 독립 변수의 수가 p개일 경우 추가되는 교호 작용 항의 수는 pC2 개가 된다. 식 (6)은 변수 3개에 대해 교호 작용 항이 추가된 다중 회귀 모델의 형태를 보여준다.
| (6) |
2.3 핸들링 및 조타감의 주관/객관 성능 간 상관 관계 모델링 프로세스
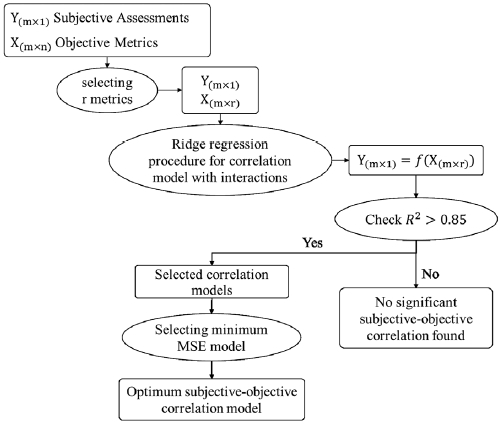
본 논문에서는 앞서 설명한 교호 작용을 포함한 다중 선형 회귀 모델의 계수들을 능형 회귀를 기반으로 추정하여 상관 관계 모델을 구축한다. 종속변수로는 주관적 평가 항목을 활용하고 독립변수로는 객관적 측정 항목을 사용한다. 모델링 과정은 Fig. 1과 같이 진행된다. 먼저 모델에 적용할 교호 작용 항을 포함한 독립 변수의 개수의 최대값을 계산한다. 학습 세트(Training set)의 수가 m 개일 경우 독립 변수의 개수는 m-1 개보다 작아야 자유도로 인한 문제가 발생하지 않는다. 따라서, 교호 작용 항을 포함한 상관 관계 모델의 독립 변수의 최대 개수는 m-2 개이다. 이를 기반으로 상관 관계 모델의 형태를 구성한다. 객관적 측정 항목 n 개이고 그 중 상관 관계 모델에 사용되는 지수 r 개라면 nCr 개 조합의 모델들을 구성할 수 있다. 모든 조합의 모델들을 능형 회귀를 기반으로 학습 세트로 모델링을 진행한다. 모델링이 완료된 상관 관계 모델들 중 미리 설정한 결정 계수(R-squared) 값의 기준을 만족하는 모델들을 선별한다. 선별된 모델들 중 시험 세트(Test set)에 대한 평균 제곱근 오차(RMSE: Root mean square error)가 가장 낮은 모델을 최종적으로 채택한다.
Modeling process of correlation between subjective and objective performance for handling and steering feel
3. 핸들링 및 조타감 주관/객관 성능 데이터
이번 장에서는 2 장에서 설명한 주관/객관 성능 간 상관 관계 모델링 프로세스에 이용할 핸들링 및 조타감의 주관적 평가 항목, 객관적 측정 항목과 데이터 세트에 대해 설명한다. 주관적 평가 항목은 독일의 AMS(Auto Motor und Sport)11) 사의 핸들링과 조타감 평가 항목을 사용한다. 객관적 측정 항목은 ISO 4138,12) ISO 740113)의 핸들링 시험과 ISO 13674-1,14) ISO 13674-215)의 조타감 시험의 성능 지수를 사용한다. 자세한 항목은 Table 1과 Table 2에 기재했다.
Subjective assessments
Objective metrics
차종은 12 차종으로 8 차종을 학습 세트로 사용하고 나머지 4 차종을 시험 세트로 사용한다. 학습 세트의 수에 따라 상관 관계 모델에 사용 가능한 독립 변수 개수는 6 개이다. 따라서, 본 논문에서는 식 (7)과 같이 객관적 측정 항목 3 개와 교호 작용 항 3 개로 구성된 상관 관계 모델을 사용한다. 여기서 SA는 핸들링 혹은 조타감 주관적 평가 항목을 나타내며, OM1, OM2, OM3은 모델링을 위해 선택된 핸들링 혹은 조타감 객관적 성능 지수 3 개를 의미한다.
| (7) |
4. 모델링 결과 및 분석
4.1 주관/객관 성능 간 상관 관계 모델링 결과
이번 장에서는 3 장의 데이터 세트를 이용하여 상관 관계 모델링을 진행한 결과에 대해 분석한다. Table 3은 본 논문에서 제안한 방법으로 구축된 핸들링 및 조타감 두 가지 모델의 계수 및 절편 값들을 보여준다.
Selected objective metrics of handling and steering feel
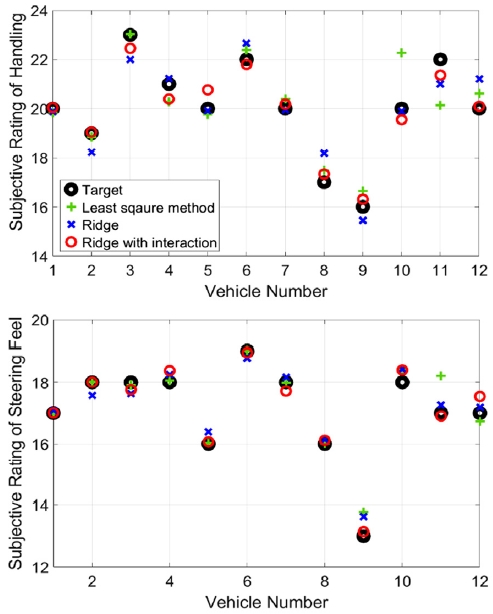
이 모델의 정확도와 신뢰도를 평가하기 위해 기존의 최소 자승법 기반 다중 선형 회귀 모델과 능형 회귀 기반의 다중 선형 회귀 모델을 본 논문에서 제안한 모델과 비교한다. 비교 대상 모델들은 제안된 모델과 계수의 개수를 동일하게 하기 위해 객관적 측정 항목을 6개 사용한다. Fig. 2는 각 차량 별 핸들링 및 조타감 주관적 평가 점수 예측결과를 보여준다. 세로축은 예측한 주관적 평가 점수이고 가로축은 차량의 번호이다. 차량은 1번부터 8번까지는 학습 세트, 9번부터 12번까지는 시험 세트로 이용되었다.
Results of subjective assessments estimation
그리고 Table 4는 모델 별 학습 세트에 대한 결정 계수 값을 보여주며 Table 5는 시험 세트에 대한 예측 값의 평균 제곱근 오차를 보여준다.
Coefficient of determination (R-squared)
RMSE (Root mean square error)
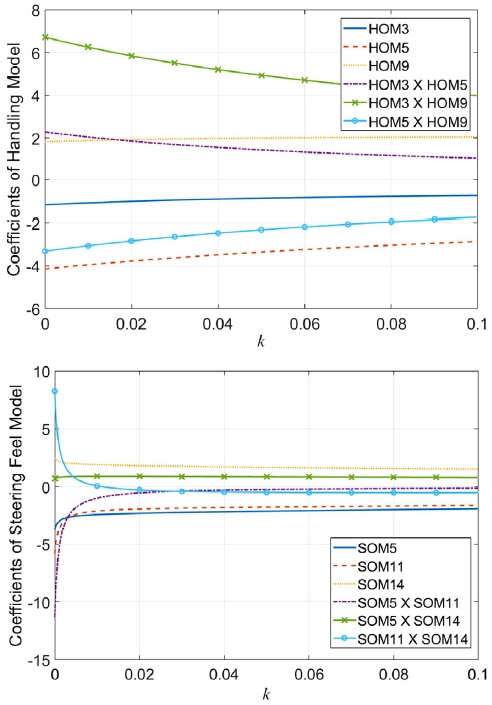
Fig. 3은 상관 관계 모델의 정규화 상수 k에 따른 계수 값들의 변화를 보여주는 Ridge plot이다. Ridge plot은 계수 값이 0에서 멀수록 해당 독립 변수가 주관적 평가 점수에 끼치는 영향도가 크다는 것을 의미한다. 또한 k값의 따른 계수 값의 변화율이 크다는 것은 해당 독립 변수가 다중공선성을 유발시킨다는 것을 의미한다.
Ridge plot of correlation models
4.2 주관/객관 성능 간 상관 모델링 결과 분석
회귀 모델의 경우 일반적으로 0.9 이상의 결정 계수 값을 가지면 샘플 데이터에 대해 해당 모델이 적합하다는 것을 의미한다. 4.1 절의 최소 자승법 기반 다중 선형 회귀 모델의 학습 세트에 대한 결정 계수 값은 핸들링은 0.9510, 조타감은 0.9984로 높은 정확도를 가진다. 하지만 시험 세트에 대한 예측 오차는 핸들링과 조타감 각각 2.3704, 0.5798로 다른 모델들에 비해 높은 오차를 보이고 있다. 이는 다중공선성의 발생 혹은 이상점의 존재로 인한 과적합 현상이 발생했을 가능성이 있다는 것을 의미한다.
반면 능형 회귀 모델의 경우 핸들링은 0.6943, 조타감은 0.1732의 최소 자승법 기반의 회귀 모델보다 비교적 낮은 오차를 보인다. 이는 과적합 현상을 완화시키는 능형 회귀 모델의 특징이 시험 세트에 대한 예측 오차를 줄이는 것에 효과가 있었음을 의미한다. 그러나 능형 회귀 모델의 경우 결정 계수 값은 핸들링이 0.8510, 조타감이 0.9208로 모델의 학습세트에 대한 적합도는 다른 모델들에 비해 낮았다.
마지막으로 본 논문에서 제안한 교호 작용 항이 포함된 능형 회귀 모델은 객관적 측정 항목을 3 개 적게 사용했음에도 불구하고, 학습 세트에 대한 결정 계수가 핸들링은 0.9388, 조타감은 0.9626로 모두 0.9보다 높았다. 또한 시험 세트에 대한 예측 오차도 핸들링은 0.1792, 조타감은 0.1198로 가장 낮았다. 이는 교호 작용 항이 핸들링 및 조타감 주관/객관 성능 간 상관 모델의 정확도 향상에 효과가 있었음을 보여준다.
Table 3의 핸들링 모델에서 교호 작용 항을 제외한 나머지 독립변수들의 계수 값들을 보면 롤 각 구배(Roll angle gradient)와 요 속도 증폭(Yaw rate overshoot)은 작을수록, 롤 각 게인(Roll angle gain)은 클수록 더 높은 주관적 평가 점수가 계산된다. 이를 통해 AMS 사에서는 입력 대비 응답이 크고 요 감쇠비(Yaw damping ratio)가 큰 차량이 높은 핸들링 점수를 받음을 예상할 수 있다. 이러한 특성은 일반적으로 과소조향(Understeer) 특성이 작은 차량에서 주로 나타난다. 요 속도 증폭의 계수는 -3.2312, 롤 각 구배와 롤 각 게인의 교호 작용의 계수는 4.7013로 독립 변수들 중 가장 높은 값을 가졌으며 이는 두 변수가 핸들링 점수에 주는 영향도가 크다는 것을 의미한다. Fig 3을 보면 핸들링에 사용된 독립변수들은 k값의 변화에 따라 계수 값의 변동이 작다. 이는 모든 변수들에 대해 다중공선성 현상의 발생 정도가 작았음을 의미한다.
조타감 모델에서는 횡가속도 손실(Lateral acceleration at 0 Nm), 조타 토크 손실(Steering torque at 0 deg)과 같이 조향계의 마찰로 인한 히스테리시스(Hysteresis) 특성은 작을수록, 조타 토크 구배(Steering torque gradient at 0.03 g)는 클수록 점수가 높게 계산된다. 교호 작용 항이 아닌 독립변수들의 영향도는 모두 컸다. 교호 작용 항 중 -2.1538의 계수 값을 가지는 횡가속도 손실과 조타 토크 손실 간의 교호 작용을 제외한 나머지 교호 작용들의 계수 값들은 각각 0.8738, 0.9854로 비교적 낮았다. Fig. 3을 보면 횡가속도 손실과 조타 토크 구배 간의 교호 작용 항과 조타 토크 손실과 조타 토크 구배 간의 교호 작용 항이 k값의 변화에 따라 계수의 감소 정도가 매우 크다는 것을 알 수 있다. 이와 같은 현상은 능형 회귀에서 다중공선성을 일으키는 변수에 대해 발생한다. 즉, 해당 교호 작용 항들은 다중공선성을 발생시키는 변수들이며, 이를 완화하기 위해 능형 회귀의 정규화 과정에서 계수 값이 감소되었음을 알 수 있다.
5. 결 론
본 논문에서는 핸들링 및 조타감의 주관/객관 성능 간 상관 관계를 다중 회귀를 사용하여 모델링을 진행했다. 다중 회귀의 문제점인 다중공선성의 해결을 위해 능형 회귀를 이용하여 상관 관계 모델링을 진행했다. 또한, 모델의 형태는 주/객관 성능 간 상관 관계 모델의 독립 변수로 사용되는 객관적 측정 항목 간의 교호 작용을 고려하기 위해 객관적 측정 항목 간의 곱으로 이루어진 항을 추가한 다중 회귀 모델을 사용했다. 이 방법의 적용을 위한 사례로 AMS 사의 핸들링 및 조타감의 주관적 평가 점수와 ISO 4138, ISO 7401의 핸들링 시험과 ISO 13674-1, ISO 13674-2의 조타감 시험의 객관적 측정 항목 간의 상관 관계 모델링을 진행했다. 구축된 모델의 정확도와 신뢰도를 평가하기 위해 최소 자승법 기반의 다중회귀 모델, 교호 작용 항이 포함되지 않은 능형 회귀 모델과 비교하였다. 모델링 결과는 다음과 같다.
- 1) 능형 회귀를 사용한 모델들은 그렇지 않은 모델보다 시험 세트에 대한 예측 오차가 낮았으며 이는 과적합 현상이 완화되었음을 알 수 있다.
- 2) 교호 작용 항을 포함한 능형 회귀 모델이 그렇지 않은 능형 회귀 모델보다 결정 계수가 높았고, 시험 세트에 대한 예측 오차도 낮았다. 이를 통해 교호 작용 항이 주관/객관 성능 간 상관 관계 모델의 정확도 및 신뢰도 향상에 효과가 있음을 입증했다.
- 3) 핸들링 및 조타감의 주관/객관 성능 간 상관 관계 모델에 선정된 독립변수들의 계수를 확인했을 때 그 값들이 공학적으로 일관적인 경향을 보였다.
이러한 결과들을 통해 교호 작용 항을 포함한 능형 회귀 모델링 방법론이 주관/객관 성능 간 상관 관계 모델에 매우 효과적임을 입증했다.
본 논문에서는 상관 관계 모델의 형태로 일차항과 교호 작용 항의 합을 사용했다. 하지만 차량 시스템은 높은 비선형성을 가지고 있다. 따라서 주관적 평가 항목과 객관적 측정 항목 간에는 비선형 관계도 존재할 가능성이 높다. 향 후에는 이러한 차량 특성의 비선형성을 고려할 수 있도록 상관 관계 모델에 비선형 항을 추가하는 방법에 대해 연구할 것이다.
Nomenclature
| N : | the number of observations |
| p : | the number of dependent variables |
| yi : | the response at observation i |
| xip : | data of pth dependent variable at observation i |
| βp : | coefficient of pth dependent variable |
| xi : | data of dependent variables, a vector of length p at observation i |
| β0 : | intercept of regression model |
| β : | coefficients of regression model, a vector of length p, respectively |
| X : | data of dependent variables matrix |
| y : | response matrix |
| k : | nonnegative regularization parameter |
Subscripts
| SA : | subjective metrics |
| OM : | objective metrics |
| HOM : | objective metrics of handling |
| SOM : | objective metrics of steering feel |
References
-
A. Mihailescu, S. Poltersdorf and L. Eckstein, “Customer‐Oriented Evaluation of Vehicle Handling Characteristics,” Encyclopedia of Automotive Engineering, pp.1-17, 2014.
[https://doi.org/10.1002/9781118354179.auto021]
-
G. Gil Gómez, M. Nybacka, E. Bakker and L. Drugge, “Correlations of Subjective Assessments and Objective Metrics for Vehicle Handling and Steering: a Walk through History,” International Journal Vehicle Design, Vol.72, No.1, pp.17-67, 2016.
[https://doi.org/10.1504/IJVD.2016.079191]
-
H. Kim J. Han and J. H. Yang, “Review on Subjective and Objective Assessments of Ride Comfort, Handling and Steering Feeling,” Transactions of KSAE, Vol.24, No.1, pp.59-66, 2016.
[https://doi.org/10.7467/KSAE.2016.24.1.059]
-
G. de Paula Eduardo, “Manual Steering Objective Reference Data Definition based on Subjective Evaluation Correlation,” SAE 2011-36-0031, 2011.
[https://doi.org/10.4271/2011-36-0031]
- J. Kim, “A Study on Vehicle Steering Feel Using Objective Measurement,” Transactions of KSAE, Vol.15, No.4, pp.161-170, 2007.
- J. Kim, Y. Kim and Y. Yoon, “Analysis of Transient Maneuvers for Objectifying Evaluation of Vehicle Stability,” Transactions of KSAE, Vol.14, No.1, pp.167-175, 2006.
-
B. Jang, K. Yi, C. Jung, J. Lee, Y. Cha, J. Park and J. Park, “Correlation of Subjective and Objective Measures of On-center Handling,” SAE 2014-01-0128, 2014.
[https://doi.org/10.4271/2014-01-0128]
- D. Lee, C. Cho and C. Hong, “Research of the Correlation between Subjective and Objective Evaluation of the Static Steering Effort,” KSAE08-S0139, pp.836-842, 2008.
-
D. Crolla, D. Chen, J. Whitehead and C. Alstead, “Vehicle Handling Assessment using a Combined Subjective-Objective Approach,” SAE Transactions, Vol.107, pp.386-395, 1998.
[https://doi.org/10.4271/980226]
-
M. Nybacka, X. He, G. Gómez, E. Bakker and L. Drugge, “Links between Subjective Assessments and Objective Metrics for Steering,” Int. J. Automotive Technology, Vol.15, No.6, pp.893-907, 2014.
[https://doi.org/10.1007/s12239-014-0094-7]
- Verlag Motor Presse Stuttgart GmbH & Co. KG, Auto Motor und Sport, https://www.auto-motor-und-sport.de, , 2020.
- International Organization for Standardization, ISO 4138:2012 Passenger Cars - Steady-State Circular Driving Behaviour - Open-Loop Test Methods, 2012.
- International Organization for Standardization, ISO 7401:2011 Road Vehicles - Lateral Transient Response Test Methods - Open-Loop Test Methods, 2011.
- International Organization for Standardization, ISO 13674-1:2010 Road Vehicles - Test Method for the Quantification of On-Centre Handling - Part1: Weave Test, 2010.
- International Organization for Standardization, ISO 13674-2:2016 Road Vehicles - Test Method for the Quantification of On-Centre Handling - Part2: Transition Test, 2016.