4 휠 독립 조향 차량의 핸들링 성능 향상을 위한 자가 동조 기반 적응형 모델 예측 제어 알고리즘 개발

1. 서 론

최근 차량의 핸들링 성능 및 선회 안정성을 향상시키기 위해 전륜 조향(Front Wheel Steering, FWS), 후륜 조향(Rear Wheel Steering, RWS), 4 휠 조향(Four Wheel Steering, 4WS), 독립 조향(Independent steering) 등 여러 조향 모드 및 다양한 제어 방법에 관한 연구가 이루어지고 있다. 기존 전륜 조향 시스템을 사용하는 상용차들은 일반적으로 선회 시 언더스티어(Under-steer) 특성을 나타낸다. 이러한 특성으로 인해 차량의 핸들링 성능은 상대적으로 낮아질 수 있으며 토크 벡터링(Torque vectoring) 및 후륜 조향(Rear wheel steering) 시스템과 같은 제어 기법 및 시스템을 이용하는 연구들이 핸들링 성능뿐만 아니라 다양한 주행 상황에서의 안정성 확보를 위해 수행되고 있다.

기존 연구들 중 차량의 핸들링 성능 향상을 위한 연구들은 다음과 같다. Yih 등¹⁾은 능동적 조향 개입을 통해 차량의 핸들링 특성을 제어할 수 있는 물리적 방법론을 제안하였다. Kim 등²⁾은 타이로드 방식의 SBW(steer-by-wire) 기반 독립 조향 제어 알고리즘을 개발하여 설계 공간성 확보 및 차량의 핸들링 안정성을 향상 시켰다. 또한 운전자의 조향 부담을 줄이고 핸들링 성능 및 선회 안정성을 향상시키기 위해서는 4 휠을 독립적으로 제어하는 기술이 필요하기 때문에 많은 기업 및 연구소 그리고 대학에서는 4WIS(4 wheel independent steering)와 관련된 다양한 연구가 이루어지고 있다. Hang 등³⁾은 FTSMC(fast terminal sliding mode controller)를 기반으로 SBW 시스템을 갖춘 4 독립 조향 전기차를 개발하였다. Te 등⁴⁾은 Hamilton 에너지 함수를 기반으로 4WD/4WS 자율주행 전기차의 경로 추종 및 횡 방향 안정성 제어를 위한 계측적 차량 제어 전략을 제안하였다. Zhang 등⁵⁾은 향상된 FWS 방법과 SBW가 융합된 OIS(omni-directional independent steering) 기법과 효율적 공간 확보를 위한 조향 시스템의 제어 전략을 갖춘 시스템 알고리즘을 제안하고, 이를 기반으로 높은 기동성 및 적응성을 갖춘 4WD/4WS 전기차를 개발하였다. Wang 등⁶⁾은 유압식 휠 드라이빙 시스템을 기반으로 오프로드 차량의 주행 성능을 향상시키는 기법을 제안하였다. Zong 등⁷⁾은 4WID/4WIS 전기차의 액츄에이터 고장을 방지하기 위해 재구성이 가능한 제어 할당 체계를 기반으로 FTC(fault tolerant control)방법론을 제안하였다. Hua 등⁸⁾은 4 휠 독립 구동 및 조향 휠을 갖춘 이동성 로봇 플랫폼을 설계하였으며, Ishak 등⁹⁾은 오버스티어 특성을 갖춘 인휠모터 기반 4 휠 독립 조향 전기차를 개발하였다. 또한 박장희 등¹⁰⁾은 바디 슬립각 및 요구 요 변화율을 줄이기 위해 모델 예측 제어 기반 4 휠 조향 제어 알고리즘을 개발하였다. 기존 연구들을 살펴보면 4 휠 조향 제어 시스템을 포함하는 다양한 조향 시스템을 이용해 차량의 핸들링 및 선회 시 차량 안정성을 향상시켰으며, 하드웨어적 설계 방법 및 다양한 제어 방식들이 개발되었다. 하지만 기존의 방법들의 경우 합리적 제어 성능 확보를 위해 다양한 주행 환경에서 급격하게 변화되는 시스템의 불확실성을 고려한 제어 파라미터들을 재설정해야 하는 한계점이 존재하는 것으로 확인되었다.

기존 연구의 한계점을 극복하기 위해 본 연구에서는 자가 동조 기반 적응형 모델 예측 제어 알고리즘을 제안한다. 핸들링 성능 향상을 위해 선회 시 언더스티어 특성을 갖는 차량의 목표 물리량을 뉴트럴 스티어(Neutral-steer) 기준 요 변화율로 정의하였고, 목표 물리량 추종을 위해 모델 예측 제어(Model predictive control, MPC) 기반 4 휠 독립 조향 제어 알고리즘을 제시하였다. 모델 예측 제어 알고리즘은 시스템의 수학적 모델을 이산화 하여 선형적으로 상태를 예측하고 목적함수 기반 최적 입력 값을 도출하는 제어기이다. 하지만 모델 예측 제어 알고리즘은 불확실성이 비교적 크게 존재하는 시스템을 예측하고 최적화 한다면 합리적인 제어 입력 값 도출이 어렵다는 한계점이 있다. 따라서 본 연구에서는 차량의 요 변화율과 목적함수의 입력 가중치 관계를 1차 함수로 정의하고, 재귀적 순환 최소 자승법(Recursive Least Square, RLS) 기반 1 차 함수의 비례상수를 실시간 추정하였다. 추정된 비례 상수는 자가 동조 및 MIT 규칙¹¹⁾ 기반 적응 알고리즘에 이용되어 입력 가중치를 갱신하고, 주행 상황에 따라 갱신된 입력 가중치는 MPC의 최적 조향 입력 값 도출을 위한 목적함수에 이용되었다. 합리적 최적 제어 입력 도출을 위해 시스템의 물리적 제약 조건이 반영되었으며 본 연구 단계에서는 역 위상 제어 전략을 제약 조건으로 반영하여 목표 요 변화율을 추종할 수 있도록 하였다. 최적 입력 값은 전륜의 경우 운전자 입력에 더해지는 개별 보조 및 후륜 단독 개별 조향으로 계산되도록 설계되었다.

본 연구에서 제안된 적응형 모델 예측 제어 알고리즘의 성능 평가는 Matlab/Simulink 환경에서 스텝 조향(Step steer) 및 위브(Weave) 조향 시나리오에서 수행되었다. 성능 평가 결과 분석을 바탕으로 향후 동 위상 조향 제어를 위해 적응형 알고리즘의 적용 및 적응 지연 시간을 줄이기 위한 고도화 방법을 계획한다.

2. 자가 동조 기반 적응형 모델 예측 4 휠 독립 조향 제어

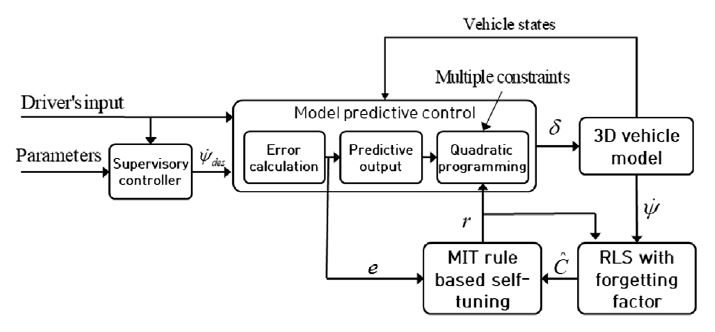
Fig. 1은 본 논문에서 제안하는 자가 동조 기반 적응형 모델 예측 제어 알고리즘의 모델 개략도를 보여준다.

Fig. 1

Model schematics for adaptive model predictive control

Fig. 1에서 오차 e는 요 변화율(Yaw rate)의 오차로써 관리 제어기(Supervisory controller)에서 운전자 입력에 따라 계산된 요구 요 변화율을 이용하여 계산된다. 차량의 현재 요 변화율과 입력 가중치 r 을 이용해 추정된 비례 상수 $$ \widehat{C}$$은 오차와 함께 입력 가중치를 갱신하면서 모델 예측 제어 알고리즘에 적용되어 최적 조향 입력 각을 도출한다. 계산된 조향 입력 각은 전륜 조향의 경우 운전자 조향 입력에 개별 조향 제어 입력이 더해지고, 후륜의 경우 개별 제어 입력이 단독으로 적용될 수 있도록 설계되었다. 다음 절부터 모델 예측 제어, 제어 알고리즘에 적용된 물리적 제약 조건, 자가 동조 규칙 및 적응 알고리즘에 대해 기술한다.

2.1 모델 예측 제어 알고리즘

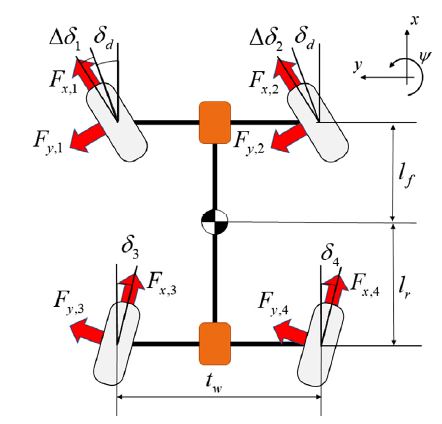
Fig. 2는 제어 알고리즘의 수학적 모델 도출을 위한 차량 2 차원 평면 모델을 보여주며, 현 연구 단계에서는 차량의 종방향 속도는 일정하다고 가정하였다.

Fig. 2

Vehicle planar model used for controller design

Fig. 2의 차량 평면 모델을 기반으로 다음과 같은 횡 및 요 비선형 동역학 모델을 도출할 수 있다.

$\[ m\left({\dot{\upsilon }}_y+{\upsilon }_x\dot{\psi }\right)=\begin{array}{l}{F}_{y,1}\cos \left({\delta }_d+\mathrm{\Delta }{\delta }_1\right)+F_{y,2}\cos \left({\delta }_d+\mathrm{\Delta }{\delta }_2\right)\\ +F_{y,3}\cos {\delta }_3+F_{y,4}\cos {\delta }_4\end{array} \]$

(1)

$\[ I_z\ddot{\psi }=\begin{array}{l}{l}_f\left[F_{y,1}\cos \left({\delta }_d+\mathrm{\Delta }{\delta }_1\right)+F_{y,2}\cos \left({\delta }_d+\mathrm{\Delta }{\delta }_2\right)\right]\\ +\frac{t_w}{2}\left[F_{y,1}\sin \left({\delta }_d+\mathrm{\Delta }{\delta }_1\right)-F_{y,2}\sin \left({\delta }_d+\mathrm{\Delta }{\delta }_2\right)\right]\\ -l_r\left[F_{y,3}\cos {\delta }_3+F_{y,4}\cos {\delta }_4\right]\\ +\frac{t_w}{2}\left[F_{y,3}\sin {\delta }_3-F_{y,4}\sin {\delta }_4\right]\end{array} \]$

(2)

동역학 모델 기반 상태벡터 $$ {\left[{\upsilon }_y\dot{\psi }\right]}^T$$와 조향 입력벡터 [∆δ₁ ∆δ₂δ₃δ₄]^T 에 대한 자코비안 행렬을 도출하였고, 이를 이용해 정리된 상태 공간 선형 모델은 아래와 같다.

$\[ \dot{X}=AX+Bu \]$

(3)

$\[ X={\left[{\upsilon }_y\dot{\psi }\right]}^T, u={\left[\mathrm{\Delta }{\delta }_{1 }\mathrm{\Delta }{\delta }_2{\delta }_3{\delta }_4\right]}^T \]$

(4)

$\[ A=\left[\begin{array}{c}\frac{\partial f_{{\upsilon }_y}}{\partial {\upsilon }_y}\frac{\partial f_{{\upsilon }_y}}{\partial \dot{\psi }}\\ \frac{\partial f_{\dot{\psi }}}{\partial {\upsilon }_y}\frac{\partial f_{\dot{\psi }}}{\partial \dot{\psi }}\end{array}\right], B=\left[\begin{array}{c}\frac{\partial f_{{\upsilon }_y}}{\partial \mathrm{\Delta }{\delta }_1}\frac{\partial f_{{\upsilon }_y}}{\partial \mathrm{\Delta }{\delta }_2}\frac{\partial f_{{\upsilon }_y}}{\partial {\delta }_3}\frac{\partial f_{{\upsilon }_y}}{\partial {\delta }_4}\\ \frac{\partial f_{\dot{\psi }}}{\partial \mathrm{\Delta }{\delta }_1}\frac{\partial f_{\dot{\psi }}}{\partial \mathrm{\Delta }{\delta }_2}\frac{\partial f_{\dot{\psi }}}{\partial {\delta }_3}\frac{\partial f_{\dot{\psi }}}{\partial {\delta }_4}\end{array}\right] \]$

(5)

선형화된 2 차원 동역학 모델을 이용해 오차에 대한 정의와 함께 아래의 오차 동역학 모델을 도출하였다.

$\[ \dot{e}=A_{e}e+B_{e}u+F_{e}w \]$

(6)

$\[ e=X_{des}-X \]$

(7)

$\[ \begin{array}{cccc}{A}_e=A,& B_e=-B,& F_e={\dot{X}}_{des}-A{X}_{des},& w=1\end{array} \]$

(8)

오차에 대한 상대적 가중치를 의미하는 대각 행렬 C_e 을 이용하여 시스템 출력 y 를 아래와 같이 정의하였다.

$\[ y=C_{e}e \]$

(9)

본 연구에서는 4 휠 독립 조향 차량의 핸들링 성능 향상을 위해 목표 요 변화율 값을 아래와 같이 뉴트럴 스티어 기준 요 변화율 값으로 적용하였다.

$\[ {\dot{\psi }}_{des}=\frac{{\upsilon }_x}{L}{\delta }_f \]$

(10)

예측 제어 알고리즘 적용을 위해 오차 동역학 모델을 이산화하고, 변환된 각 행렬들을 아래첨자 d 를 이용해 나타내었다. 예측 출력 Y 와 입력에 대한 가중치 r 을 이용해 비용 함수 J 를 아래와 같이 정의하였다.

$\[ J=Y^{T}Y+r{U}^T{D}^{T}DU \]$

(11)

$\[ Y=G{e}_k+HU+F{u}_k+MW+K{w}_k \]$

(12)

$\[ G={\left[C_d{A}_d{C}_d{A}_d^2\cdots C_d{A}_d^N\right]}^T \]$

(13)

$\[ H=\left[\begin{array}{cccc}0& 0& \cdots & 0\\ C_d{B}_d& 0& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ C_d{A}_d^{N-2}{B}_d& C_d{A}_d^{N-3}{B}_d& \cdots & 0\end{array}\right] \]$

(14)

$\[ U={\left[u\left(k+1\right)u\left(k+2\right)\cdots u\left(k+N\right)\right]}^T \]$

(15)

$\[ F={\left[C_d{B}_d{C}_d{A}_d{B}_d\cdots C_d{A}_d^{N-1}{B}_d\right]}^T \]$

(16)

$\[ M=\left[\begin{array}{cccc}0& 0& \cdots & 0\\ C_d{B}_d& 0& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ C_d{A}_d^{N-2}{D}_d& C_d{A}_d^{N-3}{D}_d& \cdots & 0\end{array}\right] \]$

(17)

$\[ W={\left[w\left(k+1\right)w\left(k+2\right)\cdots w\left(k+N\right)\right]}^T \]$

(18)

$\[ K={\left[C_d{D}_d{C}_d{A}_d{D}_d\cdots C_d{A}_d^{N-1}{D}_d\right]}^T \]$

(19)

식 (11)에서 정의된 비용 함수를 2차 형태로 변환하고, 이차 계획법(Quadratic programming)을 이용한 최적 예측 제어 입력 도출을 위해 Matlab에서 제공하는 Quadprog 함수를 이용하였다. 최적 예측 제어 입력 도출 시 물리적 제약조건 두 가지(경계, 부등호 제약조건)가 적용되었으며 상세 내용은 다음 절에서 기술하였다.

3. 성능 평가

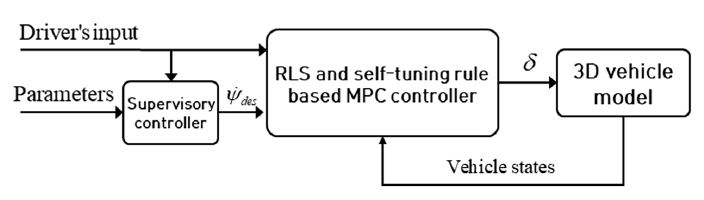
Fig. 3은 제안된 자가 동조 기반 적응형 예측 제어 알고리즘의 성능평가를 위한 모델 개략도를 보여준다.

Fig. 3

Model schematics for performance evaluation

성능평가를 위해 3 차원 차량동역학 모델이 이용되었고, 성능평가는 저속과 고속 상황에서의 스텝 조향과 위브 조향 시나리오 기반 수행되었다. 사용된 3 차원 차량 동역학 모델은 Matlab/Simulink 환경에서 구성된 차량 모델로써 6 자유도의 거동 표현이 가능하다.

차량 모델의 경우 1/4 차량 서스펜션 모델과 Pacejka 타이어 모델을 이용하였으며 비선형 차량 강체 동역학 이론이 적용되었다. 제어 알고리즘의 성능평가를 위해 적용된 스텝 조향 및 위브 조향 시나리오의 조건들은 Table 1에서 보여준다. Table 2는 성능평가를 위해 사용된 파라미터들과 언더스티어 경향을 갖는 대상 차량의 대표 물성치 및 언더스티어 계수(Understeer coefficient)를 보여준다.

Table 1

The used parameters and values

Table 2

Vehicle parameters for performance evaluation

Fig. 4

Longitudinal velocity for performance evaluation

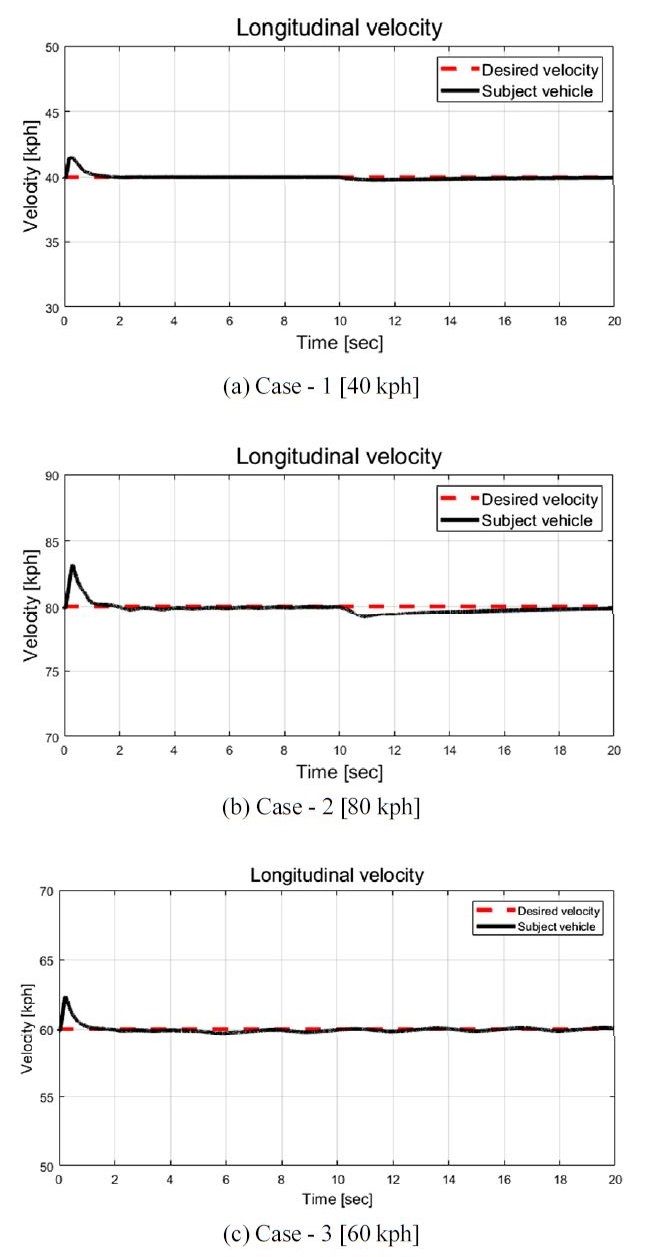
성능 평가는 스텝(Step) 조향 입력 기반 상대적 저속(40 kph)과 고속(80 kph)에서의 두 가지 시나리오와 위브(Weave) 조향 시나리오가 적용되었다. 차량의 등속 주행을 위해 LQR(Linear Quadratic Regulator) 기반 요구 종방향 속도를 추종하였다. Case-1, Case-2, Case-3에서 요구 종방향 속도를 각각 40 kph, 80 kph, 60 kph 로 정의하였다. 본 연구에서 제안된 적응형 조향 제어 알고리즘의 평가 결과는 기존 2휠 조향(전륜) 및 고정된 가중치 기반 4 휠 독립 조향 알고리즘의 평가 결과와 함께 비교 / 분석 되었다.

3.1 케이스 - 1 : 스텝 조향 (저속)

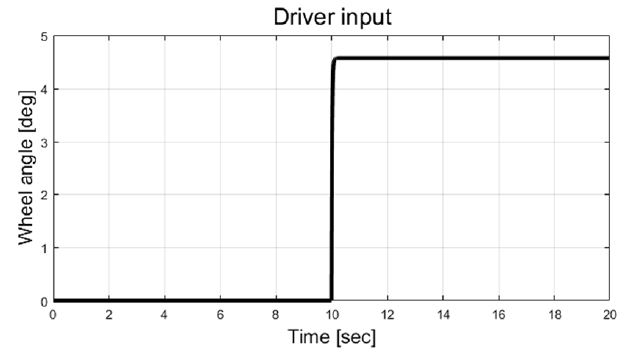
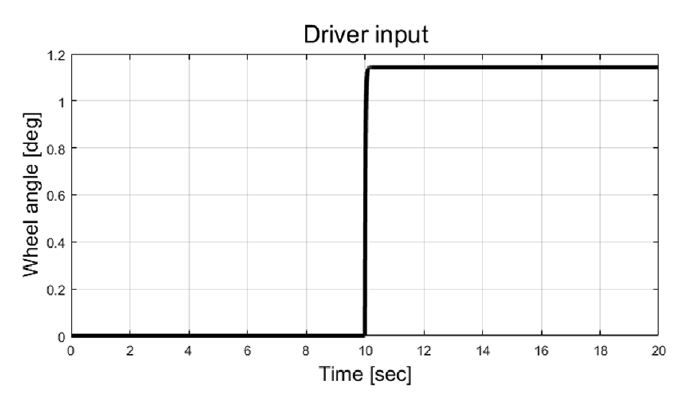
비교적 저속 상황인 Case-1의 경우 40 kph 속도로 주행 중 80도의 운전자 조향 휠 입력을 적용한 주행 상황이다. 운전자 입력에 대한 휠 각도는 Fig. 5에서 볼 수 있다.

Fig. 5

Driver input : step steering

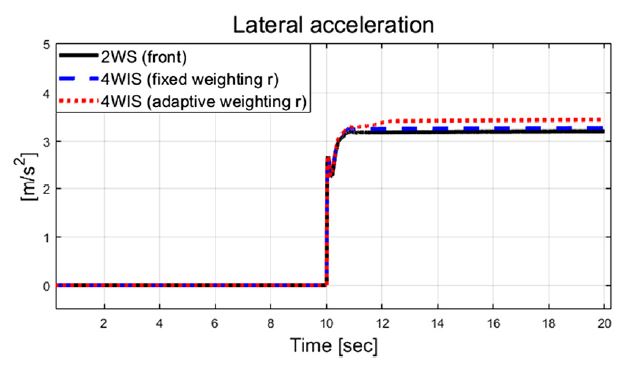
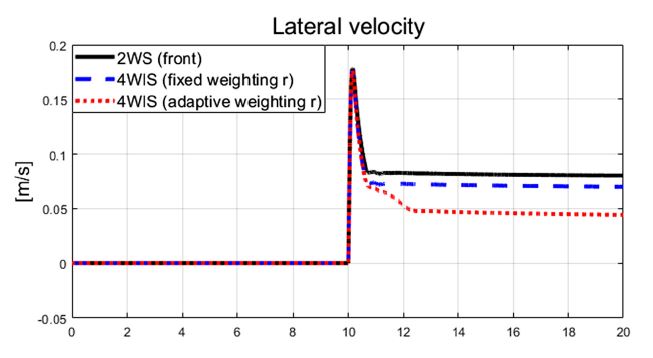
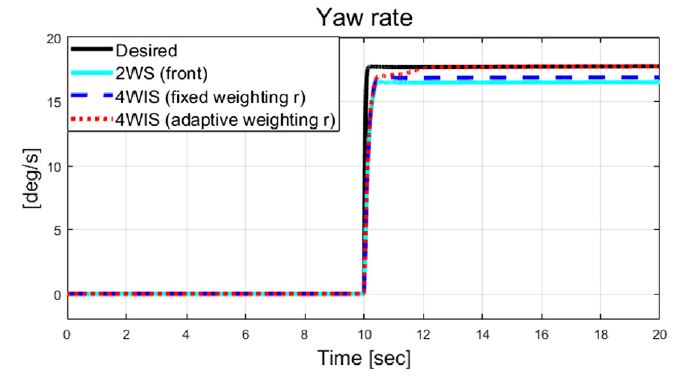
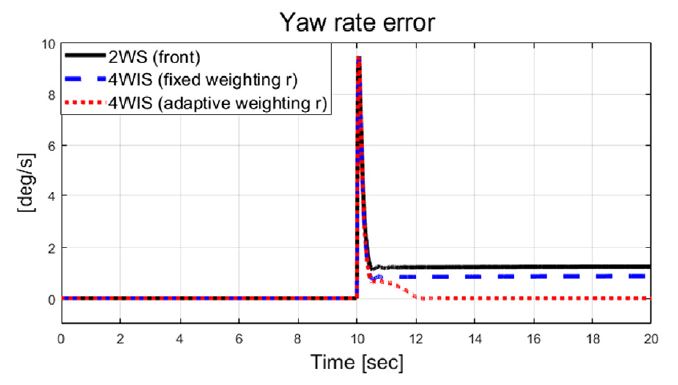
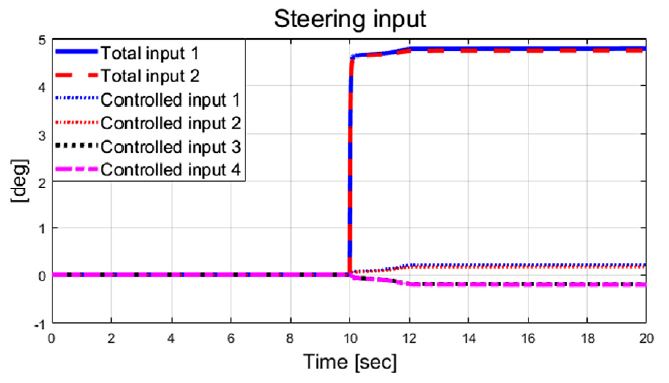
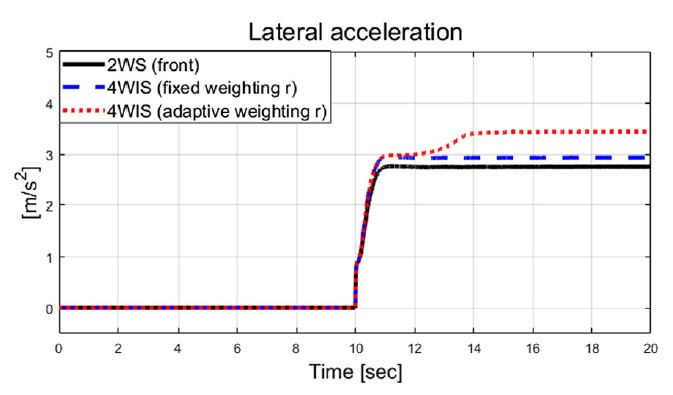
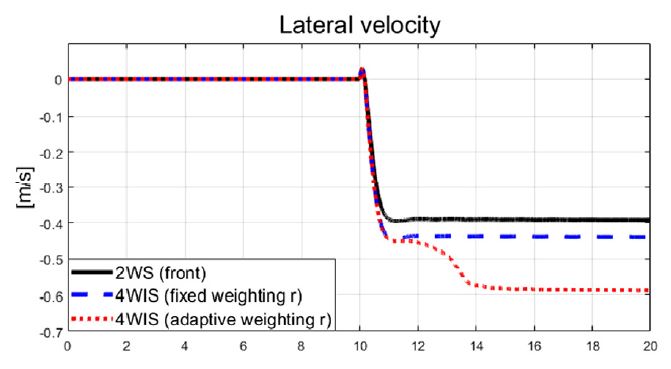
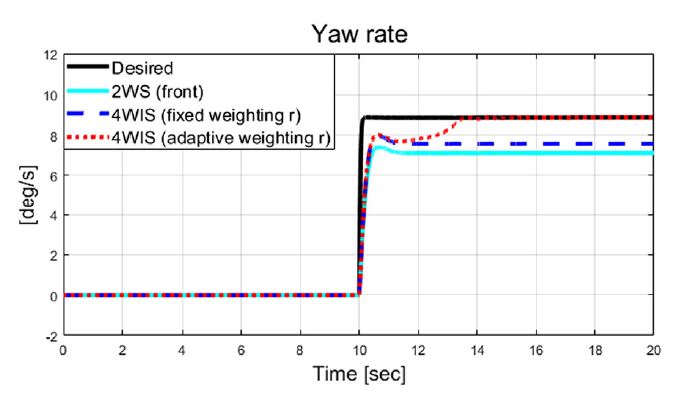
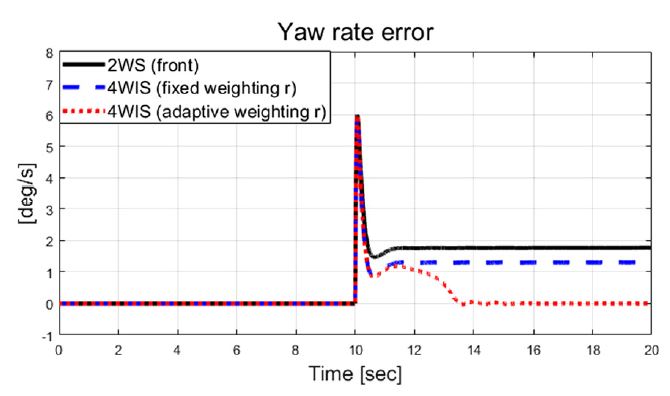
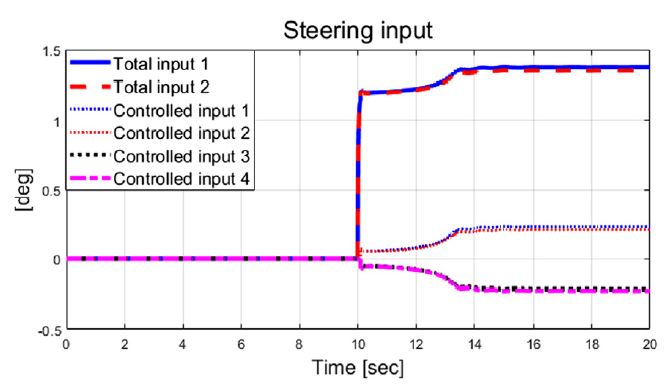
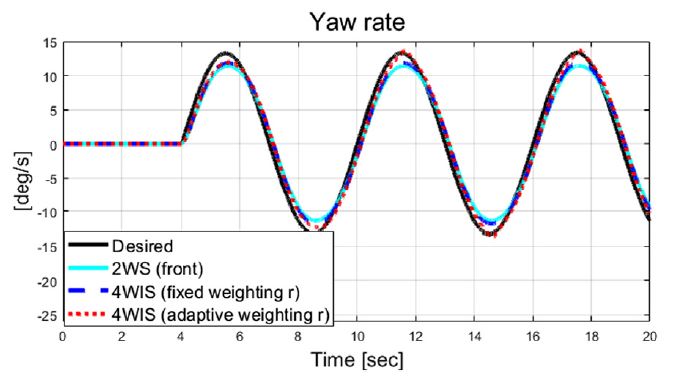
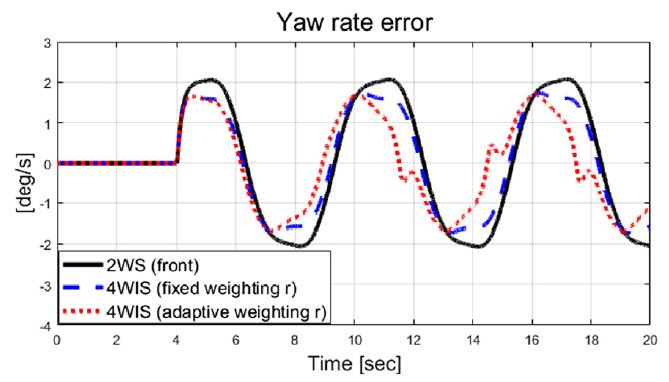
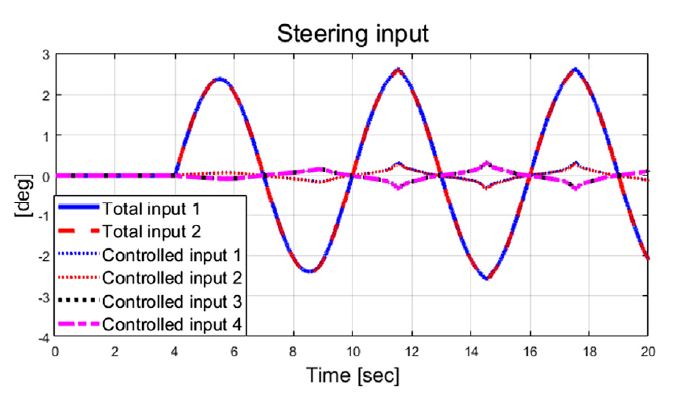
Fig. 6은 횡 가속도를 보여주고 있으며, Figs. 6~9는 비교 대상인 기존 2 휠 조향과 고정 가중치 기반 4 휠 독립 조향, 그리고 제안된 자가 동조 기반 적응 4 휠 독립 조향 알고리즘의 성능 평가 결과들을 보여준다. Fig. 7은 횡방향속도 그래프를 보여주며, 제안하는 알고리즘이 적용된 결과가 기존 시스템 대비 약 0.04 m/s의 작은 값을 보여준다. Fig. 8과 Fig. 9는 선회 시 요 변화율과 추종 오차 비교 결과를 보여준다. 결과적으로 Fig. 9에서 볼 수 있듯이, 기존 2휠 조향(전륜) 시스템 대비 제안하는 알고리즘은 정상 상태 요 변화율 오차가 약 1.24 deg/s에서 약 0.0002 deg/s 까지 줄어든 것을 확인할 수 있었다. Fig. 10에서는 Case-1에서 계산된 최적 조향 입력 값들을 보여준다.

Fig. 6

Result: lateral acceleration

Fig. 7

Result: lateral velocity

Fig. 8

Result: yaw rate

Fig. 9

Result: yaw rate error

Fig. 10

Result: steering input

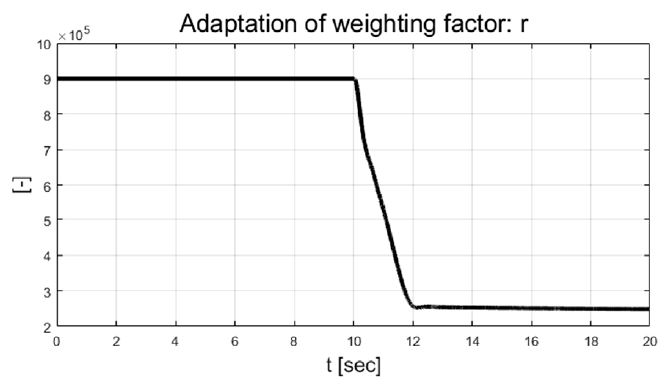
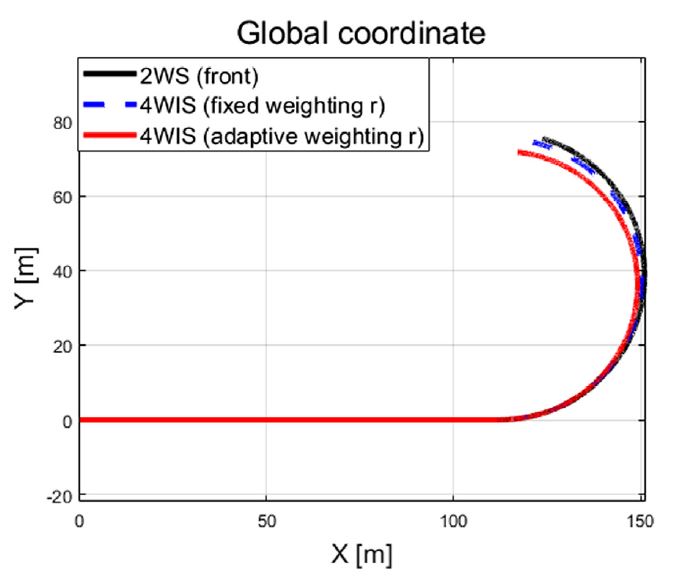
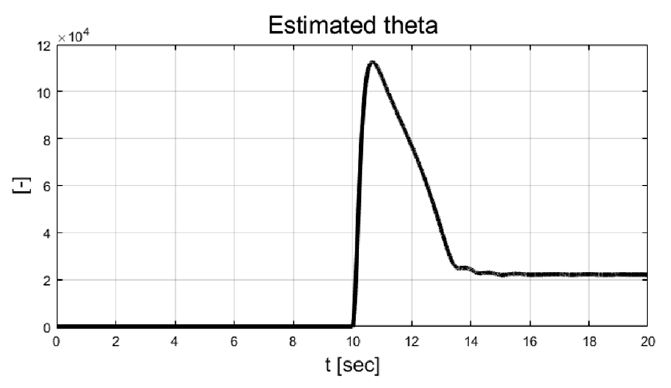
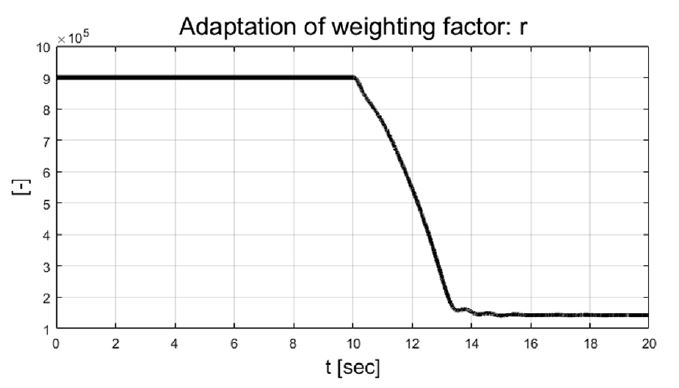
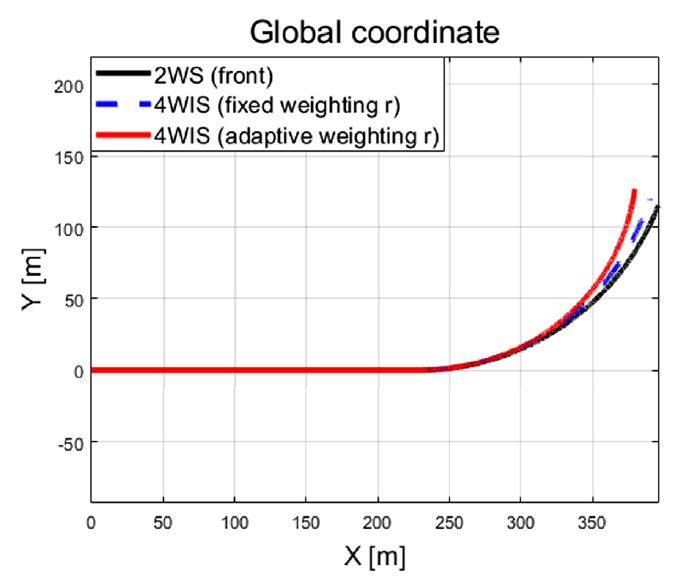
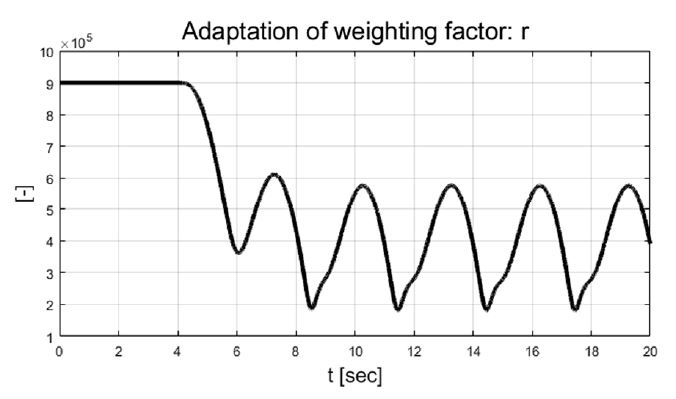
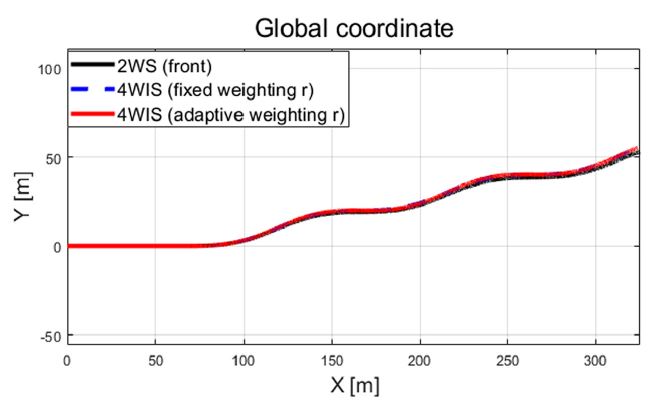
차량의 동적 상태량 및 조향 입력 값들을 살펴보면 step 조향 입력이 적용된 이후 10초에서 12초 사이의 과도 구간에서 조향 제어 입력들이 적응 알고리즘 기반 조절되는 것을 확인할 수 있다. 이는 Fig. 11의 결과처럼 추정되는 비례 상수가 특정 값으로 수렴하기까지의 시간과 관계가 있음을 확인할 수 있다. 추정된 비례상수와 요 변화율 오차에 따라 Fig. 12에서 보이는 것처럼 적응 입력 가중치가 계산되는 것을 볼 수 있다. Fig. 13은 성능평가 동안 차량의 주행 경로를 보여준다.

Fig. 11

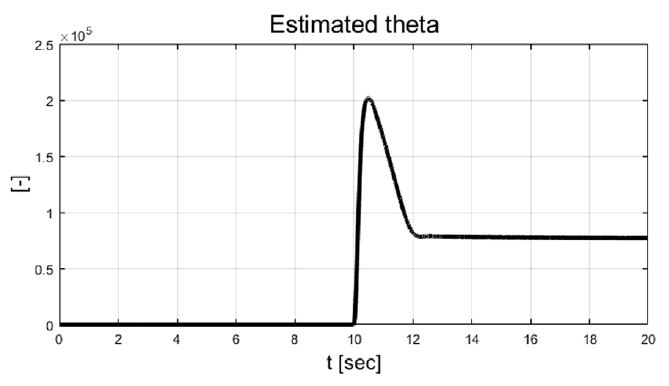
Result: estimated proportional factor based on recursive least squares with single forgetting factor

Fig. 12

Result: adaptive input weighting factor

Fig. 13

Result: trajectory

3.2 케이스 - 2 : 스텝 조향 (고속)

Case-2의 경우 80 kph 주행 중 Fig. 14와 같이 20도의 운전자 조향 휠 입력을 주었다. 즉, 차량 전륜에 약 1.14도의 휠 각도의 입력을 주었고, Fig. 15와 같이 약 3 m/s²의 횡 가속도 값을 갖는 주행 상황이다.

Fig. 14

Driver input : step steering

Fig. 15

Result: lateral acceleration

Fig. 16에서 제안하는 알고리즘은 고속 상황의 조건으로부터 횡 방향 속도가 음의 값으로 횡 슬립 현상을 보였지만, Fig. 17 및 Fig. 18의 결과 그래프에서 볼 수 있듯이 제안하는 적응형 제어 알고리즘은 요구 요 변화율을 합리적으로 추종하는 것을 확인할 수 있었다. Fig. 18의 요 변화율 오차는 2 휠 조향(전륜) 시스템의 경우 정상 상태 구간에서 약 1.77 deg/s의 요 변화율 오차를 갖는데 비해 제안하는 알고리즘은 0 deg/s에 가까운 결과를 보였다. Case-2에서의 계산된 최적 조향 입력 값은 Fig. 19에서 볼 수 있고, 추정되는 비례 상수가 특정 값으로 수렴되기까지 약 3 초의 과도 구간이 존재하는 것을 확인하였다. 낮은 속도에서 평가가 수행된 Case-1 대비 Case-2에서 과도 구간이 상대적으로 길다는 것을 확인할 수 있었다. 추정된 비례상수 및 적응 입력 가중치 결과는 각각 Fig. 20 및 Fig. 21에서 확인할 수 있고, Fig. 22는 차량의 주행 경로를 보여준다.

Fig. 16

Result: lateral velocity

Fig. 17

Result: yaw rate

Fig. 18

Result: yaw rate error

Fig. 19

Result: steering input

Fig. 20

Result: estimated proportional factor based on RLS

Fig. 21

Result: adaptive input weighting factor

Fig. 22

Result: vehicle trajectory

성능평가 결과를 보면 초기 같은 입력 가중치를 적용했음에도 실시간 추정된 비례상수와 요 변화율 오차 기반모델 예측 제어 알고리즘의 입력 가중치가 합리적으로 적응하는 것을 확인할 수 있었다. Table 3은 Fig. 13과 Fig. 22의 차량 주행 경로를 바탕으로 도출된 회전 반경 값들의 비교 결과를 보여준다.

Table 3

Comparison results of turning radius

Table 3의 결과에서 볼 수 있듯이 Case-1에서는 2 휠 조향(전륜) 시스템 보다 고정 가중치 기반 4 휠 독립 조향 제어 시스템의 회전 반경이 약 0.85 m 작은 것을 확인할 수 있다. 그리고 고정 가중치 기반 4 휠 독립 조향 제어 시스템 대비 제안하는 알고리즘의 회전 반경은 약 2.6 m 작은 것을 확인할 수 있다. 요구 값을 뉴트럴 스티어 조건의 요 변화율을 적용 하였을 때, 언더스티어 특성을 갖는 기존 2 휠 조향(전륜) 시스템 차량 대비 본 연구에서 제안된 알고리즘 기반 4 휠 독립 조향 차량이 더 작은 회전 반경을 갖는 것을 확인하였다. 제안하는 적응형 알고리즘이 입력 가중치를 갱신하면서 요 변화율 오차를 0 으로 수렴시킬 수 있었기 때문이다. 특히 고속 상황인 Case-2의 경우 확연히 줄어든 회전 반경(각각 약 10.91 m, 약 31.75 m)을 확인하였다.

3.3 케이스 - 3 : 위브 조향 (중속)

Case-3의 경우 운전자 입력으로 사인 파 조향 각 입력을 인가하는 위브 조향 시나리오가 적용되었다.

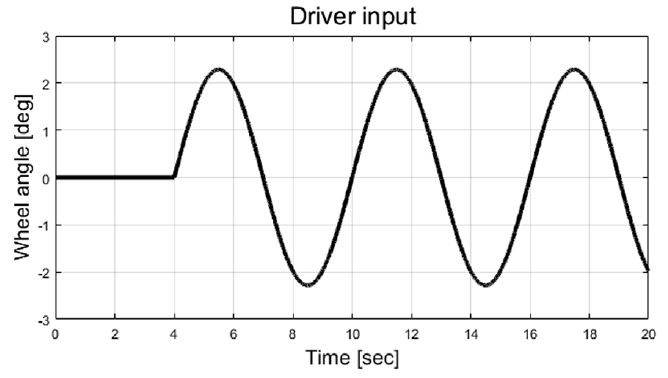
Case-1과 Case-2에서 이용된 동일 차량 파라미터 및 물리적 제약조건들이 적용되었으며, Case-4 성능 평가를 위한 입력 조건 및 모델 예측 제어 파라미터들은 Table 4에서 확인할 수 있다. 인가된 운전자 조향 휠 입력은 Fig. 23에서 볼 수 있다.

Table 4

The used parameters and values

Fig. 23

Driver input : weave steering

Fig. 24

Result: lateral acceleration

Fig. 25

Result: lateral velocity

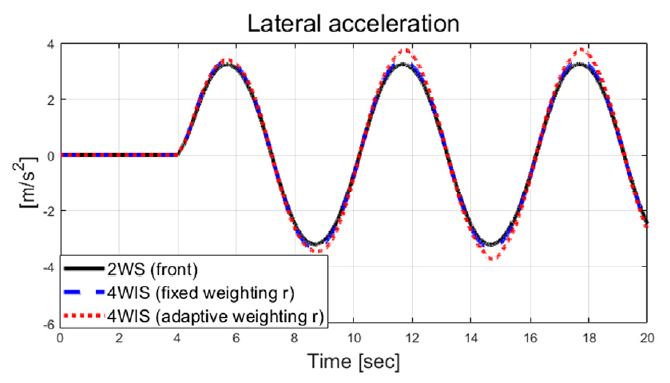
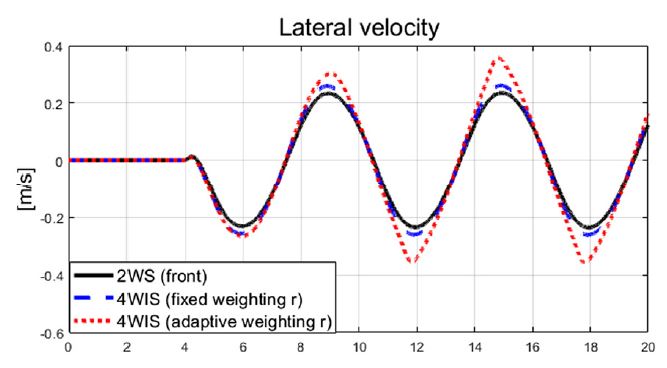
전륜 조향만 이용한 경우, 고정된 입력 가중치를 이용한 MPC 그리고 제안하는 적응형 가중치 기반 MPC를 이용한 성능 평가 결과를 비교 / 분석하였다. 본 연구에서 제안하는 알고리즘은 Fig. 26 및 Fig. 27에서 볼 수 있듯이 요구 물리량을 비교 대상 시스템들에 비해 합리적으로 추종하는 것을 확인할 수 있다. 하지만 Fig. 26을 보면, 약9초 이후부터 명확한 성능 차이를 확인할 수 있고, 이는 운전자 입력이 인가된 후 적응 지연이 존재하기 때문이다. 변화하는 조향 입력으로 인해 요 변화율 오차의 부호가 변화하는 구간이 존재하게 되고, Fig. 29에서처럼 추정 비례상수의 값도 변화한다. 그에 따라 적응 입력 가중치 값도 증가 및 감소하고, Fig. 30에서 변화 결과를 볼 수 있다. 제안된 제어 알고리즘에 의해 향상된 핸들링 성능에 의해 더 커진 횡 속도 및 가속도 결과를 Fig. 24와 Fig. 25에서 확인할 수 있다.

Fig. 26

Result: yaw rate

Fig. 27

Result: yaw rate error

Fig. 28

Result: steering input

Fig. 29

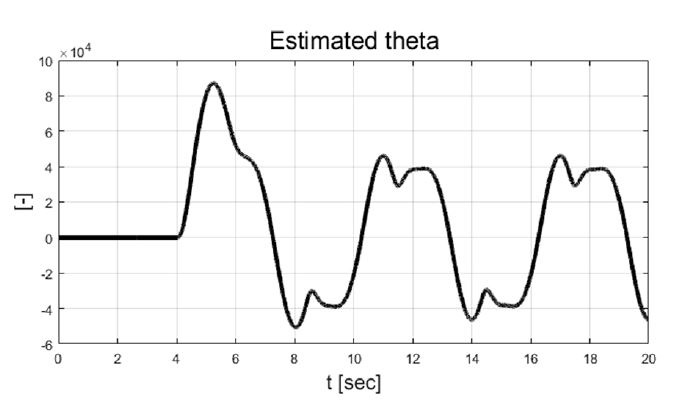
Result: estimated proportional factor based on recursive least squares with single forgetting factor

Fig. 30

Result: adaptive input weighting factor

Fig. 31

Result: trajectory

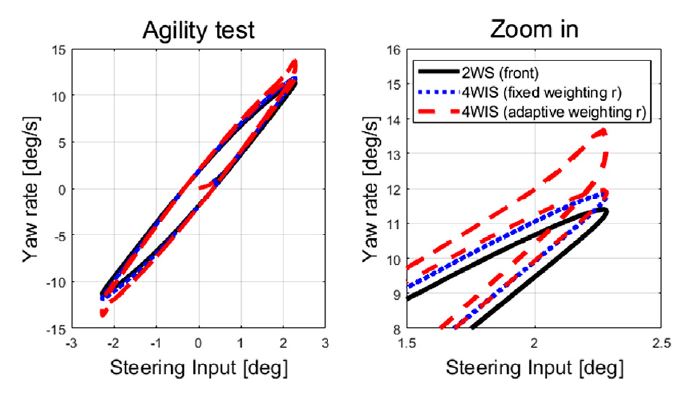
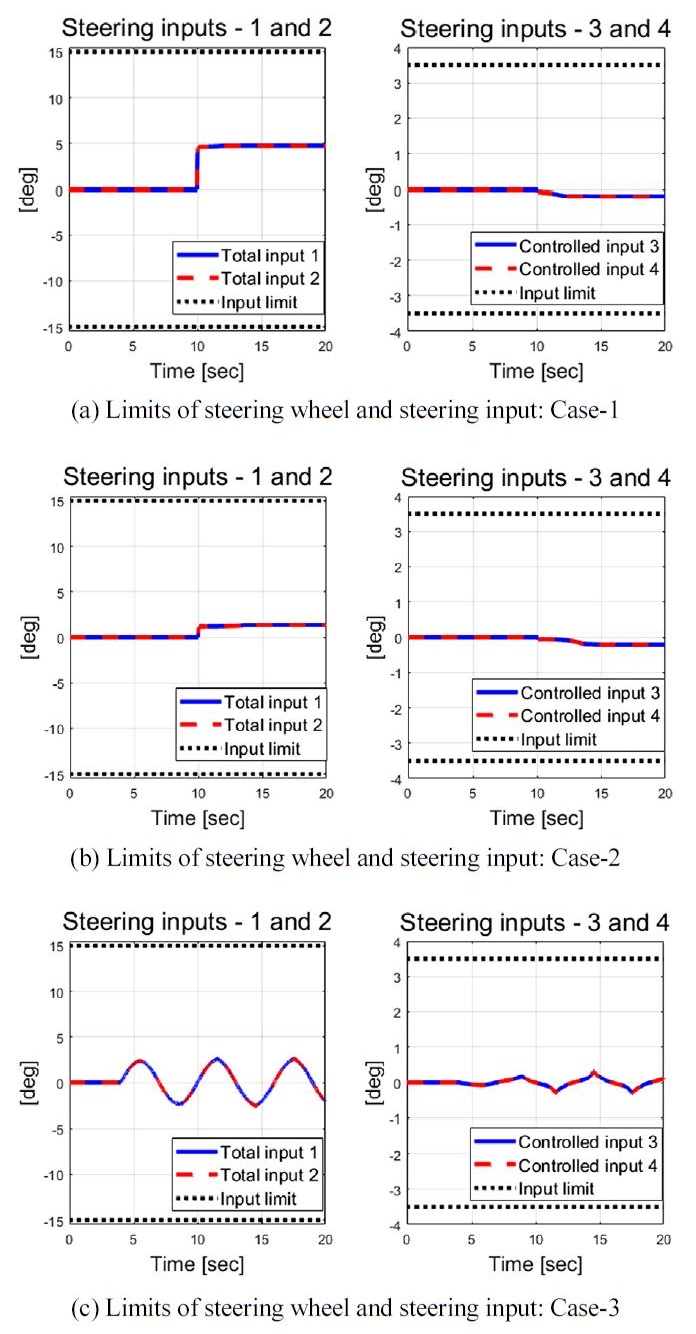
Case-3에서의 운전자 조향 휠 입력 대비 요 변화율 거동 분석을 Fig. 32에서 확인할 수 있다. Fig. 32의 오른쪽 그래프를 보면 운전자 조향 휠 입력이 많이 사용될수록 요 변화율이 상대적으로 크게 나타나는 것을 확인할 수 있다. Fig. 33과 34는 적용된 물리적 제약 조건들이 반영된 제어 입력 분석 결과를 보여준다. 도출된 최적 조향 입력값들은 조향 시스템의 조향각 한계와 조향각 변화율 한계 제약조건들이 고려되어 계산되었고, Fig. 33에서 도출된 모든 제어 입력들이 적용된 조향각 한계 제약 조건을 만족하는 것을 확인할 수 있다.

Fig. 32

Agility analysis: input steering and yaw rate

Fig. 33

Limits of steering wheel and steering input

Fig. 34

Limits of steering wheel rate and steering input

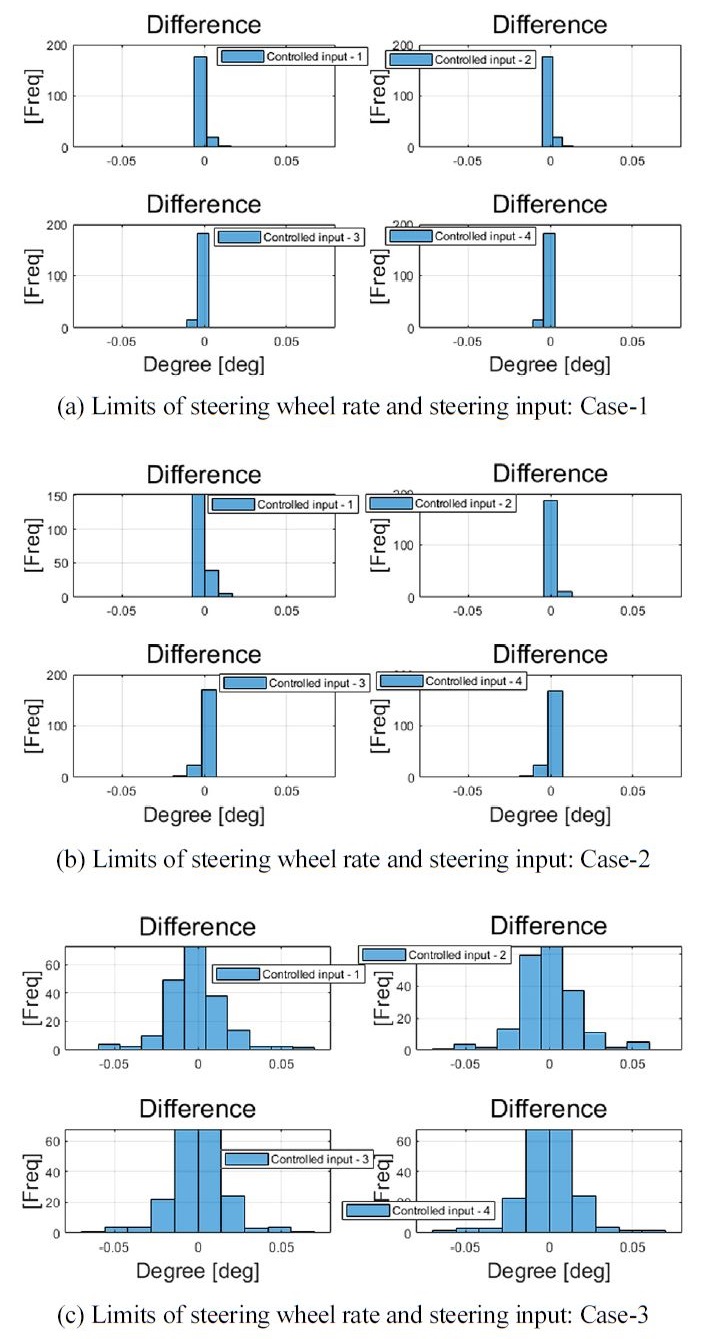
전륜 조향각은 운전자 조향 입력 각과 제어 입력 각의 합의 크기가 최대 15도인 제약 조건이 반영되었고, 후륜의 경우 제어 조향각의 크기 한계값은 3.5도로 적용되었다. 또한 역 위상 제약 조건이 적용되었기 때문에 전륜 조향각과 후륜 조향각은 반대 부호를 갖는 것을 확인할 수 있다. Fig. 34는 성능 평가 결과로 도출된 조향각의 0.1 초 간격 차이값에 대한 히스토그램을 보여준다. 적용된 조향각 변화율 한계는 20 deg/s이기 때문에 0.1 초 내 변화할 수 있는 최대 조향각은 2도이다.

Table 5는 성능평가를 위해 적용된 조향각 변화율 한계값과 성능평가 결과 도출된 모든 조향 제어 입력들의 최대값 변화율 값을 보여준다. 제약 조건으로써 적용된 조향각 변화율 한계값은 20 deg/s이고, Fig. 33과 Fig. 34에서 살펴볼 수 있듯이 모델 예측 제어 알고리즘에서 도출된 모든 최적 제어 입력 값들은 적용된 물리적 제약 조건을 만족하여 도출된 것을 확인할 수 있다.

Table 5

The calculated maximum steering wheel rate

4. 결 론

본 논문에서는 4 휠 독립 조향 시스템 제어를 위한 적응형 모델 예측 제어 알고리즘을 제시하였다. 기존 모델 예측 제어 알고리즘이 갖는 불확실성에 의한 제어 성능 저하 한계점을 극복하기 위해 입력 가중치 갱신 기반 적응형 모델 예측 제어 알고리즘을 개발하였다.

핸들링 성능 향상를 위해 요구 물리량은 운전자 입력과 속도 값을 이용해 뉴트럴 스티어 기준 요 변화율을 적용하였고, 요구 물리량을 이용한 오차 동역학 모델 기반 설계된 모델 예측 제어 알고리즘 기반 4 휠 독립 휠의 최적 조향 제어 입력 값을 도출하였다. 하지만 차량의 수학적 모델은 주행 상황에 따른 불확실성이 존재하고 이를 포함한 예측 제어를 수행했을 때, 제어 알고리즘의 성능은 부정적 영향을 받을 수 있다. 이를 극복할 수 있는 적응형 모델 예측 제어 알고리즘 설계를 위해 역 위상 조향일 때의 요 변화율과 입력 가중치 사이의 반비례 관계식을 정의하였고, 순환 최소 자승 기법을 기반으로 관계식의 비례 상수를 추정하였다. 추정된 관계식의 비례 상수는 MIT 규칙 기반 입력 가중치 갱신 알고리즘을 설계하기 위해 이용되었다. 그리고 갱신된 입력 가중치는 모델 예측 제어 알고리즘에서 최적 제어 입력 값을 도출하기 위해 이용되었으며, 이 때 조향 시스템의 최대 조향 각 및 최대 조향 변화율이 물리적 제약조건으로 반영되었다.

개발된 알고리즘의 성능 평가를 위해 스텝 조향 및 위브 조향 시나리오가 적용되었으며, 같은 초기 입력 가중치 조건에서 변화하는 요 변화율과 오차에 따라 입력 가중치가 합리적으로 갱신되는 것을 확인하였다. 성능평가 결과들을 비교 하였을 때 언더스티어 경향의 차량은 제안하는 적응형 제어 알고리즘을 이용한 경우 합리적인 핸들링 성능 향상을 확인할 수 있었다. 하지만 수학적 모델과 예측 단계에서의 불확실성을 입력에 대한 가중치 적응만으로 상쇄시키기 때문에 향후 관측기를 이용한 수학적 모델의 불확실성 추정을 계획하고 있다. 또한 성능평가 결과를 보면 비례상수가 수렴되기까지 상대적으로 적지 않은 적응 구간이 존재했다. 그러므로 향후 비례상수 추정 성능과 함께 변화하는 주행 조건에서 빠른 적응시간을 갖는 알고리즘으로의 고도화를 계획하고 있다. 또한 동 위상 제어 전략을 고려하는 제약 조건을 반영함으로써 다양한 주행 상황에서 예측 제어가 가능한 알고리즘 개발을 계획하고 있다. 개발된 적응형 모델 예측 제어 알고리즘의 신뢰성 향상을 위한 상용 소프트웨어 기반 성능 평가와 함께 프로토타입 기반 알고리즘의 검증을 계획하고 있다.

Acknowledgments

본 연구는 2019 현대자동차 미래기술 연구과제의 지원을 받아 수행된 연구임.

References

• P. Yih and J. C. Gerdes, “Modification of Vehicle Handling Characteristics via Steer-by-Wire,” IEEE Transactions on Control Systems Technology, Vol.13, No.6, pp.965- 976, 2005. [https://doi.org/10.1109/TCST.2005.854320]
• C. J. Kim, J. H. Jang, S. N. Yu, S. H. Lee, C. S. Han and J. K. Hedrick, “Development of a Control Algorithm for a Tie-Rod-Actuating Steer-by-Wire System,” Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, Vol.222, No.9, pp.1543-1557, 2008. [https://doi.org/10.1243/09544070JAUTO622]
• P. Hang, X. Chen, S. Fang and F. Luo, “Robust Control for Four-Wheel-Independent-Steering Electric Vehicle with Steer-by-Wire System,” Int. J. Automotive Technology, Vol.18, No.5, pp.785-797, 2017. [https://doi.org/10.1007/s12239-017-0078-5]
• C. Te, C. Long, X. Xing, C. Yingfeng and S. Xiaoqiang, “Simultaneous Path Following and Lateral Stability Control of 4WD-4WS Autonomous Electric Vehicles with Actuator Saturation,” Advances in Engineering Software, Vol.128, No.2, pp.46-54, 2019. [https://doi.org/10.1016/j.advengsoft.2018.07.004]
• Z. Zhang, X. Zhang, H. Pan, W. Salman, Y. Rasim, X. Liu, C. Wang, Y. Yang and X. Li, “A Novel Steering System for a Space-Saving 4WS4WD Electric Vehicle: Design, Modeling, and Road Tests,” IEEE Transactions on Intelligent Transportation Systems, Vol.18, No.1, pp.114-127, 2016. [https://doi.org/10.1109/TITS.2016.2561626]
• L. Wang, X. Liu, X. Wang, B. Fu and R. Xu, “Research on Differential Performance of Four-Wheel Independent Steering of a Hydraulic Wheel-Driving Off-Road Vehicle,” The Journal of Engineering, Vol.2019, No.13, pp.68-73, 2019. [https://doi.org/10.1049/joe.2018.8956]
• C. Zong, C. Liu, H. Zheng and J. Liu, “Fault Tolerant Control Against Actuator Failures of 4WID/4WIS Electric Vehicles,” SAE 2013-01-0405, 2013. [https://doi.org/10.4271/2013-01-0405]
• F. Hua, G. Li, F. Liu and Y. Liu, “Mechanical Design of a Four-Wheel Independent Drive and Steering Mobile Robot Platform,” IEEE 11th Conference on Industrial Electronics and Applications (ICIEA), pp.235-238, 2016. [https://doi.org/10.1109/ICIEA.2016.7603585]
• M. I. Ishak, H. Ogino and Y. Yamamoto, “Improvement of Mobility for In-Wheel Small Electric Vehicle with Integrated Four Wheel Drive and Independent Steering: A Numerical Simulation Analysis,” International Journal of Multidisciplinary and Current Research, Vol.4, pp.308-316, 2016.
• J. H. Park, S. K. Kim, J. H. Heo and K. S. Huh, “A Model Predictive Control Approach for Vehicle Stability in Four Wheel Steering Vehicles,” KSAE Annual Conference Proceedings, pp.345-347, 2015.
• B. Neogi, S. K. S. Islam, P. Chakraborty, S. Barui and A. Das, “Introducing MIT Rule Toward Improvement of Adaptive Mechanical Prosthetic Arm Control Model,” Progress in Intelligent Computing Techniques: Theory, Practice, and Application, Vol.518, No.7, pp.379-388, 2017. [https://doi.org/10.1007/978-981-10-3373-5_38]