오프셋 율을 고려한 오프셋 스트립 휜의 마찰 모델 개발

1. 서 론

최근 기술들이 제품의 소형화와 집적화(Integrated)에 집중하면서 제품의 열관리에 대한 요구는 더욱 증대되는 실정이다. 이에 따라 열관리 제품에 대한 컴팩트성 역시 강조 되고 있다. 이에 대한 요구로서 컴팩트성을 만족시키기 위한 다양한 열전달 촉진 방법 등이 제시되고 있다. 여러 방법들 중에 휜을 통한 열전달 촉진은 가장 전통적이며 널리 사용되는 방법이다. 컴팩트한 크기의 열관리 제품에 사용될 수 있는 휜은 여러 휜들 가운데 루우버 휜과 오프셋 스트립 휜이 가장 관심을 많이 받는다. 루우버 휜과 오프셋 스트립 휜은 주기적으로 주유동 방향으로 유동의 흐름을 끊어 경계층의 성장을 막아 휜 표면에서 온도 구배를 높여 열전달 효과를 증대 시킨다. 뿐만 아니라 전단층의 천이에 의한 난류 효과도 함께 기대할 수 있어 난류에 의한 열전달 촉진도 기대할 수 있어서 컴팩트한 열전달 기기에 자주 사용되는 휜들이다. 한편 기업의 개발 활동에서 고객으로부터 제품 원가 절감과 개발 기간 단축의 꾸준한 요구를 요청 받고 있으며 이것을 해결하기 위해 전산 해석을 통한 설계 및 검증 역량이 매우 중요해 졌다. 그러나 루우버 및 오프셋 스트립 휜을 포함한 열관리 제품의 전산 해석, 특히 열전달 성능 해석은 휜 모델 그 자체에 대한 막대한 해석 모델링 요구로 인해 열전달 성능 해석에 대한 삼차원 수치 해석이 매우 어려운 영역으로 여겨졌으며, 이를 대체하기 위해 일차원적인 접근과 기업의 노하우를 결합하여 이러한 휜들을 포함한 열관리 제품에 대한 성능을 예측하였다. 그러나 Mao 등,¹⁾ 김택근 등,^2,4) 김택근³⁾은 우버 휜에 대한 열다공성 모델을 개발하여 루우버 휜이 포함된 차량용 라디에이터에 대한 열전달 성능 뿐만 아니라 열피로에 의한 파손 예측을 위한 비정상 열 분포를 삼차원 수치 해석을 통해 제시하였다. 그들의 연구에서 루우버 휜에 대한 투과율과 Ergun 상수를 루우버 휜 파라미터들의 함수로 제시하였다. 오프셋 스트립 휜 열전달 성능 예측에 관한 대표적인 연구는 Manglik과 Bergles,⁵⁾ Joshi와 Webb,⁶⁾ Tinaut 등⁷⁾ 그리고 김민수⁸⁾ 등이 있다. 오프셋 스트립 휜과 관련하여 가장 많이 언급되는 모델은 Manglik and Bergles⁵⁾ 상관식이다. 김택근⁹⁾은 오프셋 스트립 휜에 관하여 다공성 매질로 취급하였고 다공성 매질로 취급된 오프셋 스트립 휜에 관한 투과율과 Ergun 상수를 오프셋 휜 파라미터들의 함수로 제시 하였다. 그러나 지금까지 제시된 다양한 오프셋 스트립 휜에 관한 마찰 저항 예측 모델들은 모두 오프셋 율 50 %을 가진다. 왜냐하면 오프셋율 50 %에서 최대 열전달 성능을 가지기 때문이다. 하지만 대량 생산 체제하에서 오프셋 율 50 %를 제작하는 것은 비용 측면과 제조 기술 측면에서 매우 도전적인 일이다. 그렇기 때문에 대량 생산 체제하에서 제작되는 오프셋 스트립 휜의 오프셋 율은 30 % 이내이다. 그러므로 만일 50 % 오프셋 율을 가지는 기존의 모델들을 이용하여 열다공성 모델을 만들면 그 삼차원 수치 해석 모델의 열전달 성능 예측은 실제 제품의 성능과 차이가 난다. 이 경우에는 해석 모델의 휜이 실제 휜의 열전달 성능보다 높아서 예측된 삼차원 수치해석 모델의 성능이 실제 제품 성능보다 우수할 것이다. 그렇기 때문에 강건한 해석 모델을 만들기 위해서는 오프셋 율을 변수로 하는 새로운 모델이 필요하였다.

2. 다공성 매질 이론 및 회귀 분석

2.2 회귀 분석

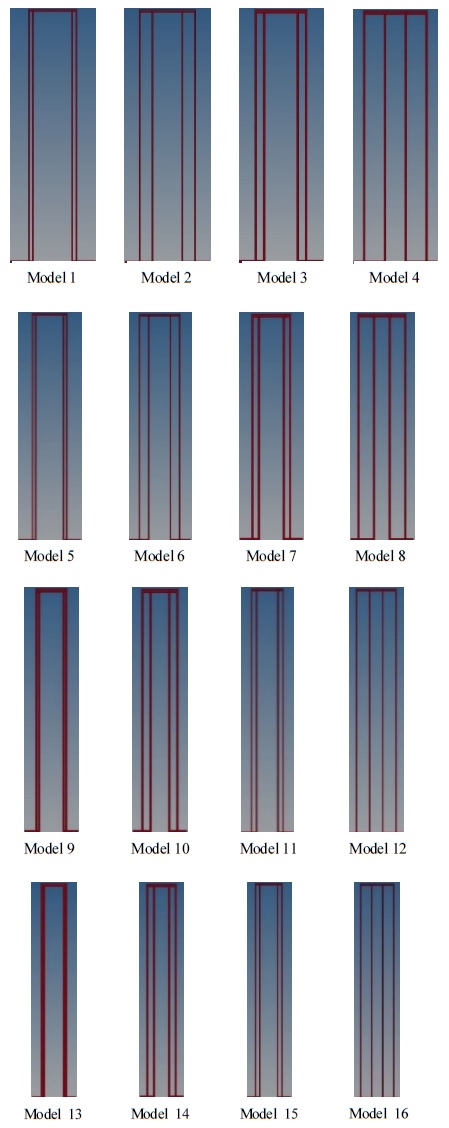
오프셋 율을 고려한 오프셋 스트립 휜의 마찰 저항 예측 모델을 개발하기 위해 휜의 FPDM, 두께, 높이, 오프셋 피치 그리고 오프셋 율을 파라미터로 선정하였으며, Table 1은 본 연구에서 오프셋 스트립 휜 에 관한 새로운 상관식을 제시하기 위해 사용된 총 16종의 모델들에 대한 파라미터 값을 보여 주고 있다. 그리고 Fig. 1은 각 모델별 전면부 형상을 나타내었다.

Table 1

Geometrical information on 16 models

Fig. 1

Frontal cross-sectional geometries for 16 models

오프셋 율 및 오프셋 스트립 휜 파라미터들로 새로운 Fanning f factor를 제시하기 위해 비선형 회귀 분석과 다중 선형 회귀 분석을 이용하였다. 이 회귀 분석을 통해 얻고자 하는 상관식을 휜 밀도, 휜 두께, 휜 피치 및 휜 높이 뿐만 아니라 오프셋 율을 변수로 갖도록 제시하였다. 오프셋 휜에 대한 마찰 계수 상관식은 다음과 같은 변수의 함수들로 나타낼 수 있다. 참고 문헌¹⁰⁾을 참조하여 비선형 회귀 분석과 다중 선형 회귀 분석을 통해 다음과 같이 구할 수 있었다.

$\[ f_i=g\left(\mathrm{R}{\mathrm{e}}_i ; \alpha , \delta , \gamma , \omega \right)+e_i \]$

본 연구의 회귀식에서 오프셋 율 20 % 이하와 30 % 이상인 경우에 대한 다른 지수값을 가짐을 알 수 있었다. 따라서 본 연구에서 제안하는 Fanning f factor 역시 오프셋 율 20 % 이하와 30 % 이상인 경우를 나눠서 상관식을 아래와 같이 제안하였다.

$\[ \begin{array}{l}f=\left(e^{k_1}R{e}^{k_{3}lnRe+k_2}\right)\\ \left(\frac{e^{b_{01}}{\omega }^{b_{11}}{\alpha }^{b_{21}}{\delta }^{b_{31}}{\gamma }^{b_{41}}}{Re}+e^{b_{02}}{\omega }^{b_{12}}{\alpha }^{b_{22}}{\delta }^{b_{32}}{\gamma }^{b_{42}}\right)\end{array} \]$

(3)

여기서

오프셋 율 20 % 이하인 경우

오프셋 율 30 % 이상인 경우

k₁ = 2.39557, k₂ = 0.49890, k₃ = 0.02443

3. 결 과

본 연구에서 제시된 상관식에 대한 평가를 위해 오프셋 율이 10 %부터 50 %까지 변화하는 모델에 대한 CFD 결과와 새로운 상관식의 결과를 비교해 보았다. 따라서 본 연구에서는 오프셋 스트립 휜에 대한 CFD를 위해 레이놀즈 수 100부터 100000까지(오프셋 율 50 %) 또는 레이놀즈 수 100부터 10000까지(오프셋 율 10 %, 20 %, 30 %)의 범위를 다뤘다. 그리고 여기서 오프셋 스트립 휜에 대한 CFD 를 위해 사용된 지배 방정식은 아래와 같으며 레이놀즈 수에 상관없이 난류 모델을 사용하였다. 왜냐하면 비교적 적은 레이놀즈 수에서도 전단층의 천이에 의해 오프셋 휜 주변은 충분한 난류 유동으로 간주 할 수 있기 때문이다. 그러므로 오프셋 스트립 휜에 적용된 지배 방정식은 RANS(Reynolds Averaged Navier-Stokes Equation)이며, 난류 모델은 k-ε 모델을 사용하였다.

여기서

그리고 해석 경계 조건은 아래와 같다. 본 연구에서 사용된 CFD 코드는 Siemens사의 STAR-CCM+ 코드를 사용하였다.

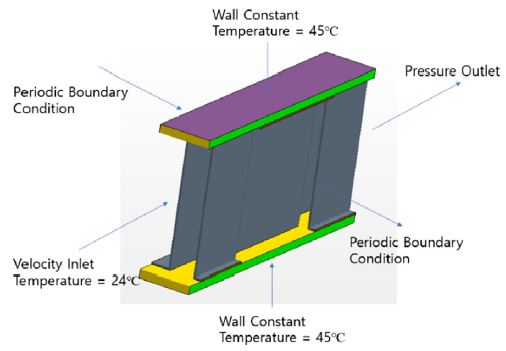
Fig. 2는 본 연구의 검증을 위해 사용된 CFD 모델에 대한 경계조건을 기술하였다. 오프셋 스트립 휜은 주유동 및 횡방향으로 형상이 반복된다. 따라서 횡방향으로는 주기조건을 사용하였으며, 오프셋 스트립 휜 윗면과 아랫면은 튜브 두께로 벽 경계조건을 부여 하였다. 그리고 주유동 입구 방향으로는 속도 경계 조건, 그리고 주유동 출구 방향으로는 압력 경계 조건을 부여 하였다. 그리고 벽면과 주유동 방향 입구측 온도차는 21°C로 설정하였다.

Fig. 2

CFD boundary condition for offset strip fins

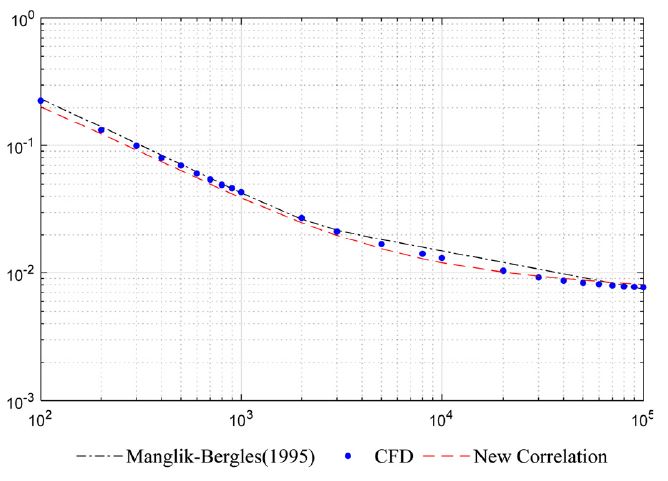
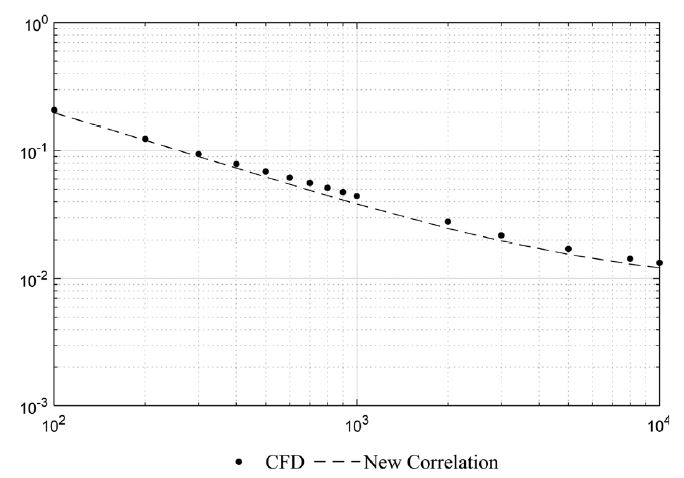
위의 CFD 해석을 수행한 후, 오프셋 율 50 % 인 오프셋 스트립 휜에 대한 Manglik and Bergles⁵⁾상관식 그리고 새로 제시된 상관식간 결과를 아래 Fig. 3부터 Fig. 6까지 비교하여 보았다.

Fig. 3

Comparison of Manglik and Bergles correlation, CFD result and new correlation at 50 % offset ratio

Fig. 4

Comparison of CFD result with new correlation at 30 % offset ratio

Fig. 5

Comparison of CFD result with new correlation at 20 % offset ratio

Fig. 6

Comparison of CFD result with new correlation at 10 % offset ratio

Fig. 3으로 부터, CFD와 Manglik and Bergles⁵⁾ 상관식간 오차는 5 % 이내이며 CFD와 새로 제시된 상관식은 3 %이내임을 알 수 있었다. 특별히 오프셋 스트립 휜이 사용되는 제품군이 주로 작동하는 구간은 레이놀즈 수 100 ~ 5000 영역이다. 이 구간에서 Manglik and Bergles⁵⁾ 상관식과 오프셋 율을 고려한 새로운 상관식 간 오차는 3 % 이내이므로 본 연구에서 제시된 오프셋 율을 고려한 오프셋 스트립 휜에 대한 상관식은 매우 정확함을 알 수 있었다.

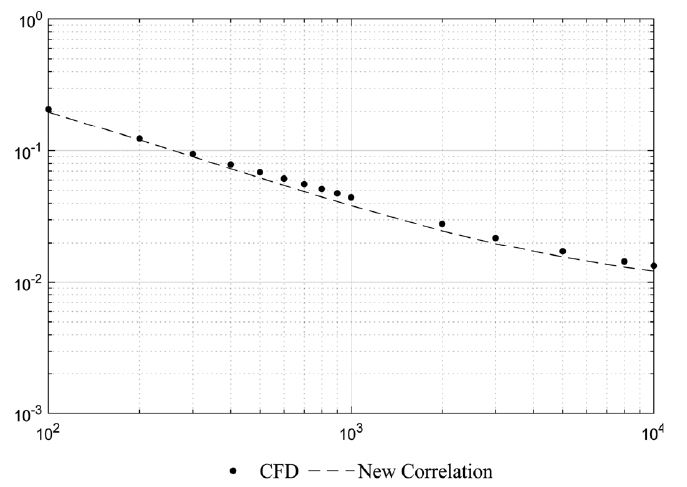
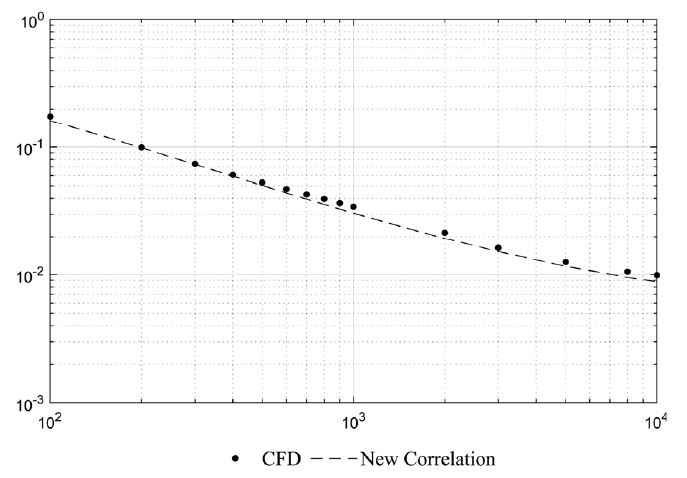
Fig. 4, Fig. 5 그리고 Fig. 6은 오프셋 율 30 %, 20 %, 10 %에 대한 레이놀즈 수에 따른 Fanning f factor 분포이다. CFD 결과와 새로운 상관식 간 오차율은 레이놀즈 수 100 ~ 5000 영역에서 3 % 미만임을 알 수 있었다.

4. 결 론

본 연구에서는 오프셋 율을 포함하여 총 5가지 변수에 대한 마찰 상관식을 제시하였다. 그리고 새로 제시된 Fanning f factor 모델에서 오프셋 율에 따라 두 가지 다른 상관식을 제시할 수 있었다. 즉 오프셋 율 20 % 이하와 오프셋 율 30 % 이상에서 각기 다른 상관식들을 제시하였다. 이 모델을 검증하기 위해 현재 까지 가장 많이 사용되고 있는 상관식, 즉 공기인 작동유체에 대하여 가장 많이 알려진 상관식인 Manglik and Bergles⁵⁾상관식과 본 연구의 CFD 결과 그리고 새로운 상관식을 오프셋 율 50 %에 대하여 비교해 보았다. 오프셋 스트립 휜을 사용하는 열관리 시스템 장치가 주로 작동하는 레이놀즈 수 100에서 5000미만에서 Manglik and Bergles⁵⁾ 상관식과 새로운 상관식간에 오차는 3 % 미만이었으며, 그 이상의 레이놀즈 수(100000 이하)에서도 CFD 결과와 새로운 상관식간 오차는 5 % 미만임을 알 수 있었다. 또한 다른 오프셋 율을 가지는 오프셋 스트립 휜에 대하여, 즉 오프셋 율 10 %, 20 %, 30 %에 대한 CFD 결과와 새로운 상관식간 오차율은 오프셋 율 50 %인 경우의 오차율과 크게 다르지 않음을 알 수 있었다. 그러므로 본 연구는 실제 오프셋 스트립 제조 환경을 고려한 오프셋 스트립 휜을 사용하는 열관리 시스템 장치에 대한 정확한 압력 강하량 및 동력을 예측할 수 있는 모델을 제시하였다.

Acknowledgments

이 논문은 2018학년도 한국기술교육대학교 교수교육연구진흥과제 지원에 의하여 연구되었습니다.

References

• S. Mao, C. Cheng, X. Li and E. Michaelides, “Thermal/Structural Analysis of Radiators for Heavy-duty Trucks,” Applied Thermal Engineering, Vol.30, Nos.11-12, pp.1438-1446, 2010. [https://doi.org/10.1016/j.applthermaleng.2010.03.003]
• T. Kim, H. Kang and J. Lee, “A Porosity Model for Flow Resistance Calculation of Heat Exchanger with Louvered Fins,” Journal of Mechanical Science and Technology, Vol.30, No.4, pp.1943-1948, 2016. [https://doi.org/10.1007/s12206-016-0353-9]
• T. Kim, “Three-dimensional Estimation of Thermal and Pressure Drop Performance of Louvered-fin Tube Heat Exchanger Using Porous Medium Approach Considering Inertia Effect,” Journal of Mechanical Science and Technology, Vol.31, No.8, pp.4011-4017, 2017. [https://doi.org/10.1007/s12206-017-0748-2]
• T. Kim, S. Lee and S. Pae, “Method of Predicting Radiator Temperature Distributions for Thermal Fatigue Analysis,” Journal of Mechanical Science and Technology, Vol.31, No.10, pp.5059-5066, 2017. [https://doi.org/10.1007/s12206-017-0954-y]
• R. Manglik and A. Bergles, “Heat Transfer and Pressure Drop Correlations for the Rectangular Offset Strip Fin Compact Heat Exchanger,” Experimental Thermal Fluid Science, Vol.10, No.2, pp.171-180, 1995. [https://doi.org/10.1016/0894-1777(94)00096-Q]
• H. Joshi and R. Webb, “Heat Transfer and Friction in Offset Strip Fin Heat Exchanger,” International Journal of Heat and Mass Transfer, Vol.30, No.1, pp.69-84, 1987. [https://doi.org/10.1016/0017-9310(87)90061-5]
• F. Tinaut, A. Melgar and R. Ali, “Correlations for Heat Transfer and Flow Friction Characteristics of Compact Plate-type Heat Exchangers,” International Journal of Heat and Mass Transfer, Vol.35, No.7, pp.1659-1665, 1992. [https://doi.org/10.1016/0017-9310(92)90136-G]
• M. Kim, J. Lee, S. Yook and K. Lee, “Correlations and Optimization of a Heat Exchanger with Offset-strip Fins,” International Journal of Heat and Mass Transfer, Vol.54, Nos.9-10, pp.2073-2079, 2011. [https://doi.org/10.1016/j.ijheatmasstransfer.2010.11.056]
• T. Kim, “Development of Friction Model for Offset Strip Fin with Separated Viscous and Inertial Resistances,” Journal of Mechanical Science and Technology, Vol.31, No.12, pp.6051-6057, 2017. [https://doi.org/10.1007/s12206-017-1149-2]
• S. Chapra and R. Canale, Numerical Methods for Engineers, 3rd Ed., McGraw-Hill, Boston, USA, 1998.