충돌회피 조향시스템의 한계성능 분석 및 회피 조향제어기 설계

1. 서 론

최근 국내외를 막론하고 자동차 OEM 및 부품 회사들이 다양한 충돌 회피 기술을 개발하고 있다. Volvo,^1,2) Benz,³⁾ Contienetal⁴⁾ 등의 회사에서는 AEB(Autonomous Emergency Brake), ESA(Emergency Steering Assist)와 같은 충돌 회피 기술을 개발하였고, 최근 개발되어 나오는 신차들에 해당 기술들을 탑재하여 판매하고 있다. 이에 대하여, 최근 Euro NCAP⁵⁾이나 UNECE 등의 차량 성능 평가 프로그램에서는 2020년 이후 판매되는 신차들은 모두 AEB와 ESA 기능을 포함하여야 하며, 이러한 충돌 회피 기술에 대하여 관련 규정 및 법규를 지정하고 있는 상황이다.

현재 개발된 AEB, ESA^6-12)는 모두 자 차량의 종/횡방향 가속도를 기반으로 하여 단순한 수식을 이용해 제동 및 급선회 회피 개입 시점을 판단하기 때문에, 회피의 성능에 대한 한계점 등의 분석이 어렵다. 또한, 선회를 기반으로 한 충돌 회피의 경우 전방 물체와의 충돌 회피 후 발생하는 차량의 거동에 대하여 안정성을 고려하지 않기 때문에 회피 후 불안정한 거동이 발생하여 다른 사고를 일으킬 수 있는 위험이 있다.

본 연구에서는 환경 센서를 통하여 획득할 수 있는 전방 차량의 속도, 가속도 등의 정보¹³⁾를 이용하여 전방 차량의 감속도를 고려한 제동 및 급선회 회피 개입 시점을 판단하고, 이를 기반으로 차량의 회피 성능을 분석하기 위한 방법을 제시한다. 또한, 회피 기술에 대한 한계 회피 성능 분석을 통해 한계 성능에 가까운 회피 제어 알고리즘을 개발하는 것을 목표로 한다.

본 논문의 구성은 다음과 같다. 2장에서는 차량에 대한 회피 성능을 분석하기 위해 전방 차량 감속도를 고려한 회피 개입 시점 판단 및 회피 성능을 나타내는 지표를 정의한다. 그 후 차량의 구동 방식 별 회피 성능을 계산하기 위한 운전자 모델을 제시하고, 성능 곡선에 대하여 비교한다. 3장에서는 회피 성능 및 운전자 모델을 기반으로 한 회피 제어 알고리즘을 소개한다. 4장에서는 개발한 회피 제어 알고리즘에 대한 시뮬레이션 결과를 소개하고, 5장에서 결론을 맺는다.

2. 회피 성능 분석

최근 충돌회피 기술의 성능에 대하여 Euro NCAP / UNECE 등에서 관련 규정 및 법규를 지정하고 있는 상황이다. 그러나, 현재 시판 중인 충돌 회피 기술인 AEB와 ESA는 모두 간단한 종/횡방향의 가속도를 기반으로 한 단순 수식을 이용하여 충돌 회피의 개입 시점을 판단하기 때문에 기술에 대한 한계 성능을 분석하는 것이 힘들다는 문제점이 있다. 이를 해결하기 위하여 본 연구에서는 먼저 회피의 성능을 분석하기 위한 성능 지표를 새롭게 정의하며, 정의한 지표를 이용하여 차량 구동 방식에 따른 회피 성능을 분석한다.

2.1 제동 및 급선회 회피 개입 시점

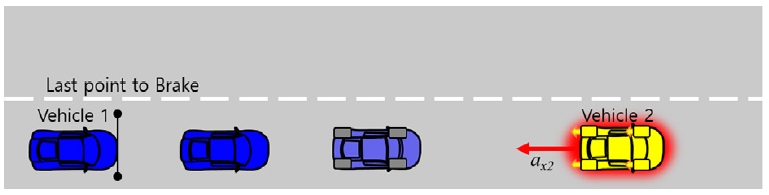
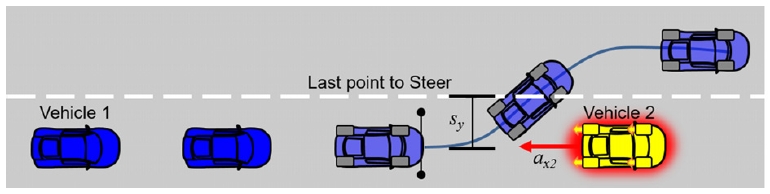
회피 성능 분석을 위한 성능 지표 정의에 앞서, 회피 기술에서 사용되는 회피 개입 시점에 대하여 알아보자. 기존의 회피 기술에서 전방 차량과의 충돌을 회피하기 위한 최소한의 제동 및 급선회 회피 개입 시점은 각각 Last to point brake와 Last to point steer라고 하며, Fig. 1과 Fig. 2는 충돌 위험 상황에서 Last to point brake/steer의 정의를 보여준다.

Fig. 1

Last to point brake

Fig. 2

Last to point steer

Last to point brake/steer은 아래의 식 (1)과 (2)에 의해 계산된다.

$\[ d_{brake}=\frac{1}{2a_{x,1}}{\left({\nu }_{x,1}-{\nu }_{x,2}\right)}^2 \]$

(1)

$\[ d_{steer}=\sqrt{\frac{2s_y}{a_{y,1}}}\left({\nu }_{x,1}-{\nu }_{x,2}\right) \]$

(2)

여기서 ax,1은 주행 차량의 감속도, vx,1과 vx,2는 주행 차량과 전방 차량의 속도, sy는 주행 차량과 전방 차량의 차폭의 합의 1/2, ay,1은 주행 차량의 횡방향 가속도이다. 그러나 위의 두 식은 주행 차량의 가속도만 고려하였을 뿐, 전방 차량의 감속도는 고려하지 않았기 때문에 실제 주행 상황에서는 위험할 수 있다. 이에 따라, 전방 차량의 감속도를 고려한 최소한의 제동 및 급선회 회피 개입 시점을 아래의 두 식으로 나타내었다.

$\[ d_{brake}=\frac{1}{2(a_{x,1}-a_{x,2})}{\left({\nu }_{x,1}-{\nu }_{x,2}\right)}^2 \]$

(3)

$\[ d_{steer}=\sqrt{\frac{2s_y}{a_{y,1}}}\left({\nu }_{x,1}-{\nu }_{x,2}\right)+\frac{a_{x,2}}{a_{y,1}}{s}_y \]$

(4)

2.2 긴급회피 성능 지표

충돌 회피에 대한 성능을 분석하기 위해 2.1에서 새롭게 도출한 회피 개입 시점을 이용한다. 특히, 본 연구에서는 급선회 기반 회피에 중점을 두어, 충돌 회피를 위해 차선을 변경하는 상황에서 성능을 분석할 수 있는 성능 지표를 두 가지로 나타내었다.

첫 번째 지표는 차량의 선회 응답성을 나타내는 필요 여유(Required margin, t_rm)이다. 필요 여유는 차량이 현재 속도로 주행하면서 충돌 회피를 위해 추가로 필요한 여유 시간을 의미한다. 필요 여유에 대한 식은 아래와 같이 계산된다.

$\[ \begin{array}{l}{t}_{rm}=t_e-t_{\mathrm{m}\mathrm{i}\mathrm{n}},\\ t_{\mathrm{m}\mathrm{i}\mathrm{n}}=\sqrt{\frac{2s_y}{a_{y,\mathrm{m}\mathrm{a}\mathrm{x}}}},\\ d_{\mathrm{m}\mathrm{i}\mathrm{n}}=t_{\mathrm{m}\mathrm{i}\mathrm{n}}{\nu }_{rel}.\end{array} \]$

(5)

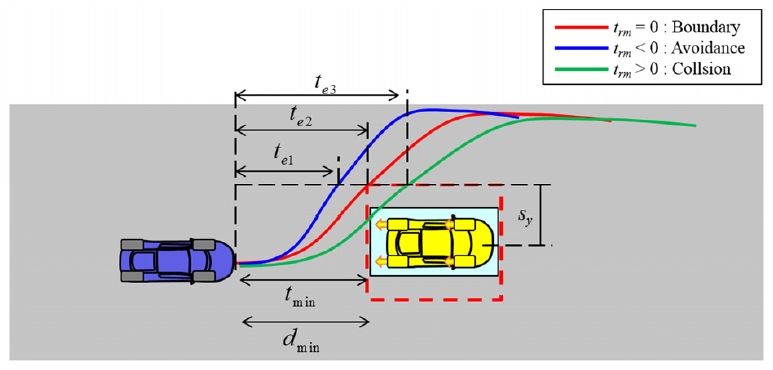
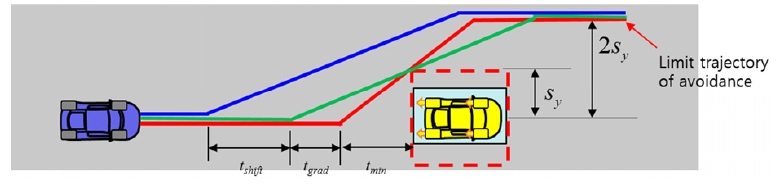
여기서 t_e는 주행 차량이 조향을 통해 횡방향으로 s_y만큼 이동할 때 걸린 시간, t_min은 조향만을 이용하여 충돌을 회피할 수 있는 최소 회피 시간, d_min은 조향만을 이용하여 충돌을 회피하는 최소 회피 거리이다. s_y와 a_y,max에 의해 필요 여유는 대상 차량의 폭과 노면의 상태를 고려한 지표가 된다. Fig. 3은 필요 여유의 값에 따라 충돌 회피의 성공 여부를 보여준다. 즉, 필요 여유의 값이 커질수록 차량의 선회 응답성이 낮음을 알 수 있다.

Fig. 3

Collision avoidance based on required margin

두 번째 지표는 차량이 회피를 한 후 차선을 변경하면서 차량의 거동에 대한 안정성을 판단하는 회피 후 안정(Stability, S)이다. 본 연구에서는 조향을 통해 충돌을 회피하면서 차선 변경을 하는 차량의 거동에 대하여 안정성을 평가하는 것이 목적이므로, 기존의 차선으로부터 목표하는 횡방향 거리와 실제 차량 거동의 최대 횡방향 거리의 차이를 회피 후 안정으로 정의하며 계산하는 식은 아래와 같다.

$\[ S=\max \left(y\right)-2s_y \]$

(6)

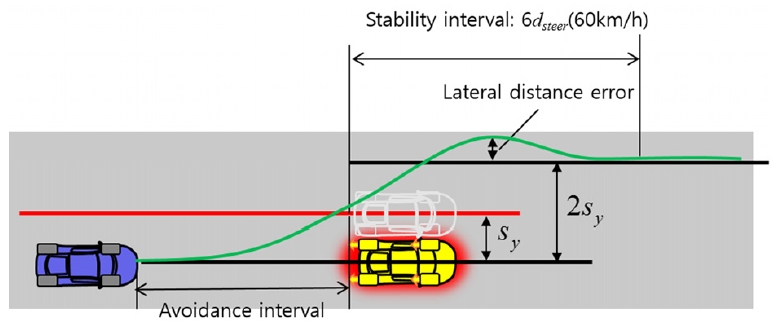
즉, 회피 후 안정은 목표 궤적에 대한 최대 횡이탈 거리를 의미한다. Fig. 4는 주행 차량의 회피 궤적을 통해 차량의 선회 응답성을 계산하는 회피 구간과 회피 후 안정성을 계산하는 회피 후 안정 구간을 보여주고 있으며, 회피 후 안정 구간에서의 d_steer (60 km/h)는 상대 속도가 60 km/h일 때의 Last to point steer를 의미한다. 회피 후 안정의 정의에 따라 그 값이 커질수록 회피 후 차량의 거동이 불안정하다는 것을 알 수 있다.

Fig. 4

Interval of avoidance and stability

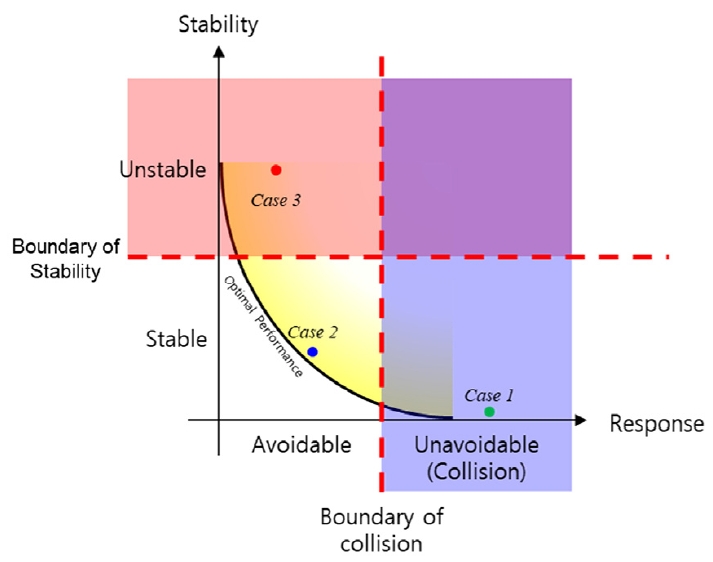
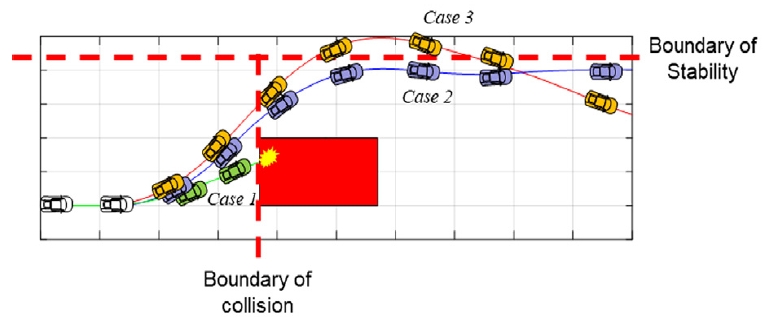
정의한 두 지표를 이용하면 차량의 한계 성능 곡선은 Fig. 5와 같이 나타낼 수 있으며, 두 지표는 작을수록 더 성능이 좋다는 것을 의미한다. 또한, Fig. 5에 표현된 Case 1~3의 실제 주행 결과를 Fig. 6에 나타내었다. Case 1은 필요 여유가 0보다 더 큰 지점에서 회피를 시도하여 충돌이 발생한 경우, Case 2는 필요 여유가 0보다 작아 회피를 성공하였으며 회피 후 차량의 거동 또한 안정적인 경우, Case 3는 회피는 성공하였으나 회피 후의 거동이 불안정한 경우이다.

Fig. 5

Limit performance using two index

Fig. 6

Driving results of each case

2.3 차량 별 회피 성능 분석

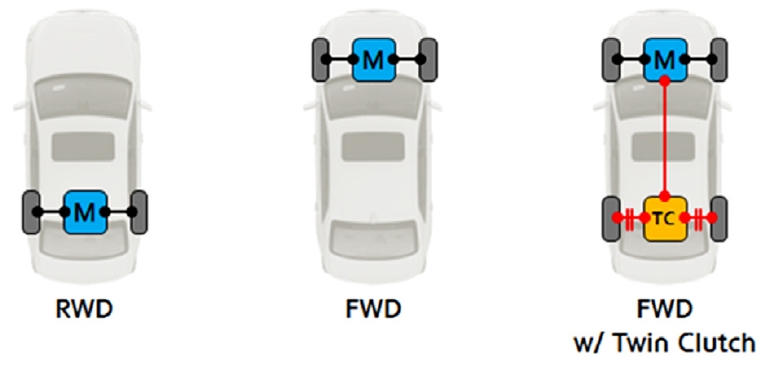
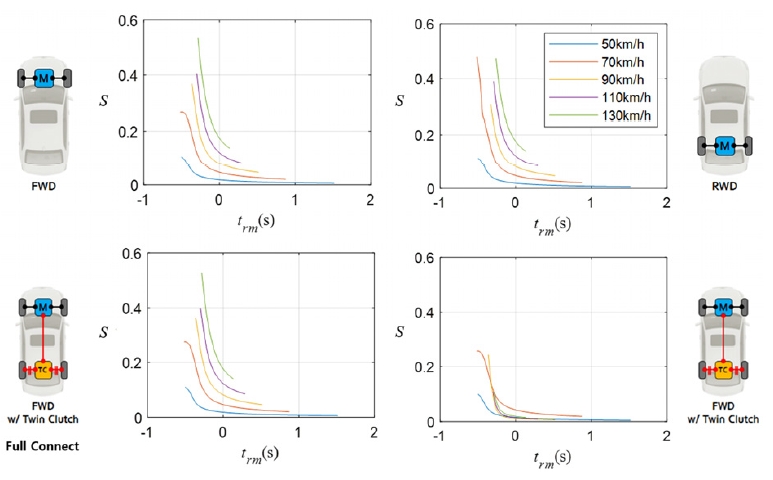
2.2에서 정의한 두 지표를 이용하여, 차량의 구동 방식에 따른 회피 성능 분석을 진행하였다. 비교할 구동 방식은 전륜 구동, 후륜 구동과 전륜 구동에서 후륜에 Twin clutch가 포함된 구동 방식으로, 총 세 종류의 구동 방식을 가진 차량에 대하여 회피 성능을 분석한다. Fig. 7은 각각의 구동 방식에 대한 구조를 보여주고 있다.

Fig. 7

Configuration of vehicle

차량의 구동 방식 별 회피 한계 성능을 분석하기 위해 주어진 상황에 최적으로 회피거동을 수행하는 차량 거동 제어기가 필요하다. 차량 거동 제어기는 조향 및 클러치 작동량을 제어변수로 하여 차량의 거동을 제어하는 역학을 한다. 차량 거동 제어기는 주어진 경우 점을 지나는 조향 및 클러치 작동량을 결정한다. 차량 거동 제어기는 Preview time 동안 주어진 경로와 주행 차량의 예측 경로 사이의 오차를 최소화하는 MacAdam 운전자 모델을^14,15) 기반으로 설계하였다. 본 연구에서는 MacAdam 운전자 모델을 수정하여 궤적 추종성과 더불어 주행 중 차량의 안정성을 고려하여 다음과 같은 시스템을 이용하였다.

$\[ \begin{array}{l}\dot{x}=Ax+Bu\\ Y=Cx\end{array} \]$

(7)

where

$$ \begin{array}{l}x={\left[\begin{array}{cccc}y& \psi & \nu & r\end{array}\right]}^T, u={\left[\begin{array}{cc}{\delta }_f& M_z\end{array}\right]}^T\\ A=\left[\begin{array}{cccc}0& {\nu }_x& 1& 0\\ 0& 0& 0& 1\\ 0& 0& -\frac{C_{\alpha f}+C_{\alpha r}}{m{\nu }_x}& \frac{b{C}_{\alpha r}+a{C}_{\alpha f}}{m{\nu }_x}-{\nu }_x\\ 0& 0& \frac{b{C}_{\alpha r}-a{C}_{\alpha f}}{I_z{\nu }_x}& \frac{a^2{C}_{\alpha f}+b^2{C}_{\alpha r}}{I_z{\nu }_x}\end{array}\right]\\ B={\left[\begin{array}{cccc}0& 0& \frac{C_{\alpha f}}{m}& \frac{{aC}_{\alpha f}}{I_z}\\ 0& 0& 0& \frac{1}{I_z}\end{array}\right]}^T, C=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\end{array}$$

여기서 y는 횡방향 변위, ψ 는 Heading angle, v는 횡방향 속도, r은 Yaw rate, M_z는 Yaw moment이다. MacAdam 운전자 모델을 이용하면 아래와 같은 Cost function을 최소화하는 제어 입력 u를 찾아야 한다.

$\[ \begin{array}{l}J=\frac{1}{T_p}{\int }_t^{t+T_p}\Delta Y^T\left(\eta \right)\left(Q_d\left(\eta \right)+Q_{risk}\left(\eta \right)\right)\Delta Y\left(\eta \right)+u^T\left(\eta \right)Ru\left(\eta \right)d\eta ,\\ \Delta Y\left(t\right)=Y_d\left(t\right)-Y\left(t\right), Y_d\left(t\right)=\left[\begin{array}{c}{y}_d\left(t\right)\\ 0\\ 0\end{array}\right], Y\left(t\right)=\left[\begin{array}{c}y\left(t\right)\\ \nu \left(t\right)\\ r\left(t\right)\end{array}\right].\end{array} \]$

(8)

여기서 T_p는 Preview time이다. Cost function을 최소화하는 입력 u를 찾기 위해 구간 [t, t+T_p]에서는 u가 일정하다고 가정한다면, J를 최소로 하는 u는 아래의 식으로 계산할 수 있다.

$\[ \begin{array}{l}{u}_{opt}\left(t\right)={\left\{{\int }_t^{t+T_p}{G}^T\left(\eta -t\right)Q\left(\eta \right)G\left(\eta -t\right)+Rd\eta )\right\}}^{-1}\\ \times \left\{{\int }_t^{t+T_p}Q\left(\eta \right)(Y_d\left(\eta \right)-F\left(\eta -t\right)x(t\left)\right)G\left(\eta -t\right)d\eta \right\},\\ F\left(t\right)=C{e}^{At},\\ G\left(t\right)=C{\int }_0^{t}F\left(\eta \right)d\eta B,\\ Q\left(t\right)=Q_d\left(t\right)+Q_{risk}\left(t\right).\end{array} \]$

(9)

위 식에서 Q와 R은 추종오차와 제어 입력에 대한 가중치 행렬이다. 식 (9)는 Reference trajectory를 추종하면서 안정성을 고려한 최적의 차량 거동 제어기이다.

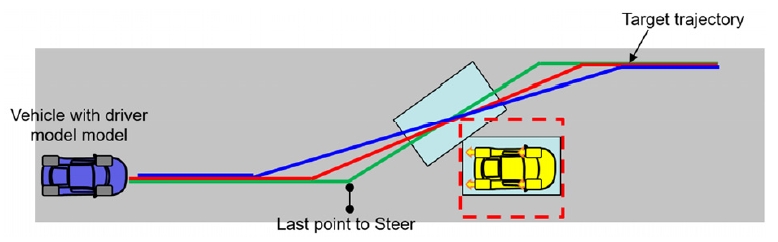
위와 같이 개발된 거동 제어기를 이용하여, 차량 별 회피 성능을 확인해야 한다. 거동 제어기는 Fig. 8에 나타난 것과 같이 두개의 경유 지점을 지나는 형태로 목표 궤적이 주어진다. 목표 궤적을 토대로 차량의 구동 방식 별 성능 곡선을 구해보면 Fig. 9와 같이 나타난다. Fig. 9에서 전륜 구동, 후륜 구동, 4륜구동 유사한 성능 곡선을 보이고 있으나 Twin clutch가 포함된 차량(연속적인 토크 분배가 가능한 차량)은 동일한 속도에서 다른 구동 방식에 비해 더 높은 성능을 보인다.

Fig. 8

Target trajectory

Fig. 9

Simulation result of 4 vehicles

3. 회피 제어 알고리즘

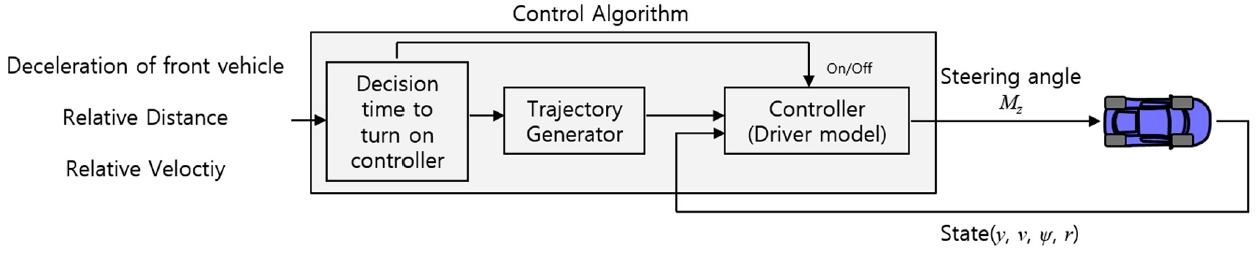
회피 운전자 모델을 기반으로 하여 자율 주행 자동차의 회피 제어 알고리즘을 설계하였다. 알고리즘은 알고리즘의 개입 시점 판단, 회피 궤적 생성, 궤적 추종 제어기 동작의 3단계로 구분되며, Fig. 10은 회피 제어 알고리즘의 전체 구조를 보여주고 있다.

Fig. 10

Configuration of control algorithm

3.1 궤적 생성기

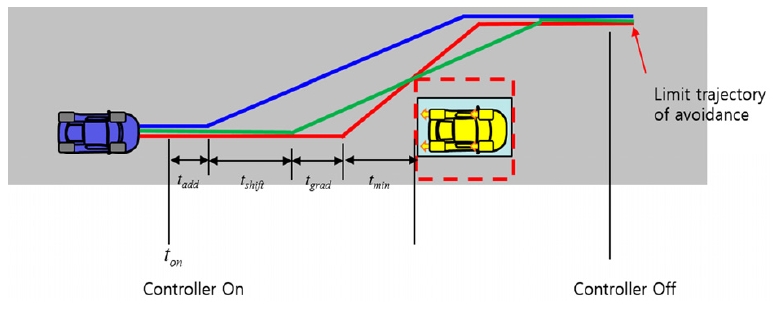
궤적 생성기는 전방 차량과의 상대 속도 및 감속도를 이용하여 충돌을 회피하는 궤적을 생성해낸다. 2.1에서 계산한 Last to point steer를 이용하여, 이론적으로 회피할 수 있는 한계 궤적을 기준으로 두고 2개의 튜닝 변수를 이용하여 궤적을 변형한다. 첫 번째 튜닝 변수는 t_grad으로, 궤적의 기울기를 조정하는 역할을 한다. 두 번째 튜닝 변수는 t_shift로, 한계 궤적의 충돌 회피 지점으로부터 여유 거리를 속도로 나누어 시간으로 나타낸 값이다. 즉, t_shift의 값을 바꾸면 궤적이 평행이동하는 내용을 효과를 보인다. Fig. 11은 궤적 생성기의 구조를 보여주고 있으며, t_min은 아래와 같은 식으로 표현된다.

Fig. 11

Structure of trajectory generation

$\[ \begin{array}{l} t_{\mathrm{m}\mathrm{i}\mathrm{n}}=\frac{d_s}{\left({\nu }_{x,1}-{\nu }_{x,2}\right)}\\ \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\\ d_s=\sqrt{\frac{2s_y}{a_{y,1,\mathrm{m}\mathrm{a}\mathrm{x}}}}\left({\nu }_{x,1}-{\nu }_{x,2}\right)+\frac{a_{x,2}}{a_{y,1,\mathrm{m}\mathrm{a}\mathrm{x}}}{s}_y\end{array} \]$

(10)

3.3 개입 시점 판단

개입 시점 판단은 제어 알고리즘이 언제 작동해야 하는지 판단하는 기준이며, 아래와 같은 식으로 표현된다.

$\[ t_{on}=t_{\mathrm{m}\mathrm{i}\mathrm{n}}+t_{grad}+t_{shift}+t_{add} \]$

(11)

여기서 차량이 생성된 궤적을 따라가기 위해서는 최소 개입 시점인 t_min 보다 여유 있게 개입해야 하므로 t_add 를 통해 그 시점을 조절하게 된다. Fig. 12는 개입 시점 판단에서 각 변수의 의미를 보여준다.

Fig. 12

Decision time to turn on controller

4. 시뮬레이션 결과

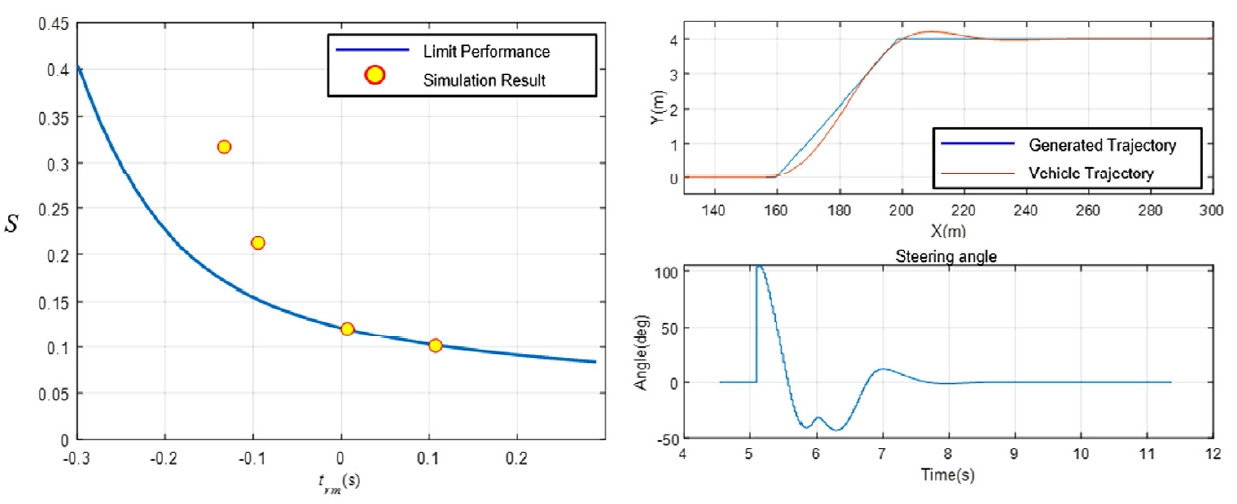
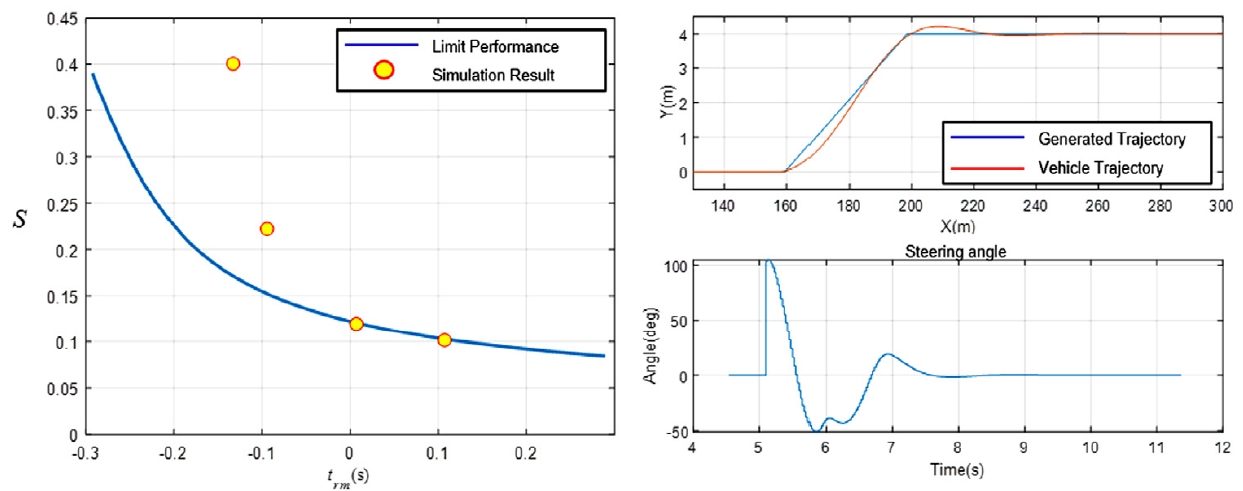
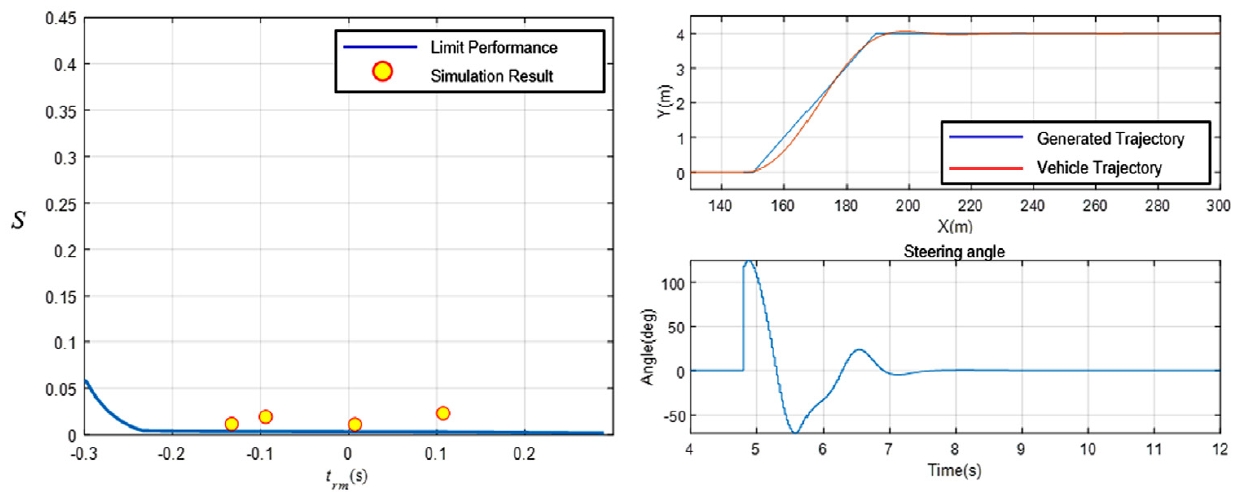
설계한 회피 제어 알고리즘을 토대로 시뮬레이션을 통해 성능을 검증하였다. 자차량의 속도가 110 km/h, 전방 차량의 속도가 50 km/h인 상황에서 검증을 수행하였으며, 자차량의 구동 방식은 각각 전륜, 후륜 구동 및 Twin clutch를 가진 차량에 대하여 비교하였다. Figs. 13~15는 각각 전륜, 후륜 구동 및 Twin clutch를 가진 차량에 대한 시뮬레이션 결과를 보여준다. Figs. 13, 14의 (a)는 전/후륜 한계 성능 결과는 유사하게 나타났으며, 시뮬레이션 결과는 t_rm = -0.14 s일 때를 제외하고 다른 경우 안정도 값이 유사하게 나타난다. Figs. 13, 14의 (b) 그래프는 t_rm = -0.1 s일 때 생성된 궤적, 실제 궤적 및 조향각에 대한 그래프를 나타낸 것이며, 전륜 및 후륜 구동에서는 성능 지표가 비슷하기 때문에 궤적 및 조향각 그래프 또한 비슷한 결과를 보인다. 전륜 구동에 Twin clutch를 가진 차량의 경우 Fig. 15(a)를 보면 전/후륜 구동보다 더 좋은 성능을 가지는 것을 알 수 있으며, Fig. 15(b)에서 목표 궤적에 대한 실제 궤적의 이탈값이 더 적게 나타난 것을 볼 수 있다. 이런 결과는 Twin clutch가 장착된 차량은 전후 좌우 구동력 분배를 통하여 추가적인 요 모멘트를 생성할 수 있기 때문이다.

Fig. 13

(a) Performance of FWD, (b) Simulation result at trm = -0.1 s

Fig. 14

(b) Performance of RWD, (b) Simulation result at trm = -0.1 s

Fig. 15

(a) Performance of FWD w/twin clutch, (b) Simulation result at trm = -0.1 s

5. 결 론

본 논문은 충돌 회피 기술에 대한 성능 평가 및 한계 성능을 기반으로 한 회피 알고리즘의 개발에 관한 연구이다. 먼저 차선 변경을 목적으로 하는 ESA에서 두 가지 성능 지표를 제시하였으며, 각각 차량의 선회 응답성과 회피 후 안정성을 의미한다. 두 지표는 모두 수치가 낮을수록 더 높은 성능을 보이도록 정의되었다. 전륜, 후륜 구동 및 전륜 구동에 Twin clutch를 추가한 세 종류의 차량에 대하여 제안된 지표들과 운전자 모델을 이용하여 성능을 평가하였다. 성능 평가에 사용된 운전자 모델은 MacAdam 운전자 모델을 기반으로 한 회피 운전자 모델이며, 간단한 직선 궤적을 제공하여 궤적 추종 후 한계 성능 곡선을 구하였다.

분석한 한계 성능 및 운전자 모델을 기반으로 자율 주행 자동차에 적용할 수 있는 회피 제어 알고리즘을 제안하였다. 회피 제어 알고리즘은 개입 시점 판단, 회피 궤적 생성, 궤적 추종의 3단계로 이루어진다. 회피 궤적 생성에서는 차량의 이론적인 한계 회피 궤적을 기준으로 2개의 튜닝 변수를 이용하여 궤적을 생성한다. 궤적 추종 제어기는 성능 분석에서 사용된 회피 운전자 모델을 이용하였으며, 회피 구간과 안정화 구간에서의 Preview time을 튜닝 변수로 이용하여 궤적을 추종한다. 마지막으로 개입 시점 판단에서는 궤적 생성기에서의 변수와 하나의 튜닝 변수를 이용하여 어느 시점에서 알고리즘이 동작하는 지 결정한다.

제안한 알고리즘을 토대로 시뮬레이션 검증을 진행하였다. 자차량 속도 110 km/h, 전방 차량 속도 50 km/h에서 차량별 한계 성능 및 알고리즘에 대한 시뮬레이션 결과를 비교하였으며, 전/후륜 구동의 경우 서로 유사한 성능을 보여주었고 Twin clutch를 갖는 차량은 다른 두 차량에 비해 더 좋은 성능을 보였다.

Acknowledgments

이 과제는 부산대학교 기본연구지원사업(2년)에 의하여 연구되었음.

References

• M. Distner, M. Bengtsson, T. Broberg and L. Jakobsson, “City Safety-a System Addressing Rearend Collisions at Low Speeds,” 21st International Technical Conference on the Enhanced Safety of Vehicles, Stuttgart, Germany, Paper No.09-0371, 2009.
• E. Coelingh, A. Eidehall and M. Bengtsson, “Collision Warning with Full Auto Brake and Pedestrian Detection - A Practical Example of Automatic Emergency Braking,” 13th International IEEE Conference on Intelligent Transportation Systems, Funchal, Portugal, 2010. [https://doi.org/10.1109/ITSC.2010.5625077]
• U. Mellinghoff, T. Breitling, R. Schoneberg and H. G. Metzler, “The Mercedes-Benz Experimental Safety Vehicle ESF 2009,” 21st International Technical Conference on the Enhanced Safety of Vehicles, Stuttgart, Germany, Paper No.09-0165, 2009.
• A. Eckert, B. Hartmann, M. Sevenich and P. E. Rieth, “Emergency Steer & Brake Assist - A Systematic Approach for System Integration of Two Complementary Driver Assistance Systems,” 22nd International Technical Conference on the Enhanced Safety of Vehicles, Washington DC, USA, Paper No.11-0111, 2011.
• Euro NCAP, Euro NCAP 2025 Roadmap, https://www.euroncap.com/en/for-engineers/technical-papers/, , 2017.
• H. Kang, D. Lee and K. Huh, “Development of Lane Change System considering Acceleration for Collision Avoidance,” Transactions of KSAE, Vol.21, No.2, pp.81-86, 2013. [https://doi.org/10.7467/KSAE.2013.21.2.081]
• T. Lee, K. Yi, J. Kim and J. Lee, “Development and Evaluations of Advanced Emergency Braking System Algorithm for the Commercial Vehicle,” 22nd International Technical Conference on the Enhanced Safety of Vehicles, Washington DC, USA, Paper No.11-0290, 2011.
• C. Chauvel, Y. Page, B. Fildes and J. Lahausse, “Automatic Emergency Braking for Pedestrians Effective Target Population and Expected Safety Benefits,” 23th International Technical Conference on the Enhanced Safety of Vehicles, Seoul, South Korea, Paper No.13-0008, 2013.
• D. Jeon, D. Sung, S, Lee and C. Kim, “Development of Emergency Driving Support System Based on Integrated Steering and Braking Control,” KSAE Spring Conference Proceedings, pp.596-603, 2013.
• T. Kang, W. Yoo, N. Kim, M. Soh, J. Kwon, T. Hong and K. Park, “A Study on the Brake Time for AEB System Considering Road Condition,” KSAE Spring Conference Proceedings, pp.737-744, 2014.
• J. Park, J. Park and K. Huh, “Decision Marking and Autonomous Emergency Steering Control for Collision Avoidance based on Model Predictive Control,” KSAE Spring Conference Proceedings, pp.214-216, 2016.
• Y. Choi, S. Kim, J. Jung and J. Yoon, “A Study on the Applicability of AEBS according to Radar Angle Using PC-Crash and Traffic Accident Database,” Transactions of KSAE, Vol.25, No.6, pp.691-701, 2017. [https://doi.org/10.7467/KSAE.2017.25.6.691]
• Y. Kwon, “Improving Multi-channel Wave-based V2X Communication to Support Advanced Driver Assistance System(ADAS),” Int. J. Automotive Technology, Vol.17, No.6, pp.1113-1120, 2016. [https://doi.org/10.1007/s12239-016-0108-8]
• C. C. MacAdam, “An Optimal Preview Control for Linear Systems,” Journal of Dynamic Systems, Measurement and Control, pp.188-190, 1980. [https://doi.org/10.1115/1.3139632]
• C. C. MacAdam, “Application of an Optimal Preview Control for Simulation of Closed-Loop Automobile Driving,” IEEE Transactions of Systems, Man and Cybernetics, Vol.11, No.6, pp.393-399, 1981. [https://doi.org/10.1109/TSMC.1981.4308705]