[ Article ]

Transactions of the Korean Society of Automotive Engineers - Vol. 28, No. 3, pp.203-210

ISSN: 1225-6382 (Print) 2234-0149 (Online)

Print publication date 01 Mar 2020

Received 09 Jan 2020 Revised 10 Feb 2020 Accepted 11 Feb 2020

DOI: https://doi.org/10.7467/KSAE.2020.28.3.203

수소연료 자동차용 액화수소탱크의 열물성 성능 예측을 위한 3차원 수치모델 개발

정수진^*^{, 1)}

; 문성준²⁾

; 박경우³⁾

; 문승재⁴⁾

1)한국자동차연구원 하이브리드동력연구센터
2)한양대학교 자동차공학대학원
3)호서대학교 기계공학과
4)한양대학교 기계공학과

Development of the Three-dimensional Numerical Model for Predicting Thermal Physical Performance in Liquefied Hydrogen Tank for Hydrogen Fueled Vehicle

Soo-Jin Jeong^*^{, 1)}

; Seong-Joon Moon²⁾

; Kyoung-Woo Park³⁾

; Seung-Jae Moon⁴⁾

1)Advanced Powertrain R&D Center, Korea Automotive Technology Institute, 303 Pungse-ro, Pungse-myeon, Dongnam-gu, Cheonan-si, Chungnam 31214, Korea
2)Graduate School of Automotive Engineering, Hanyang University, Seoul 04763, Korea
3)Department of Mechanical Engineering, Hoseo University, Chungnam 31499, Korea
4)Department of Mechanical Engineering, Hanyang University, Seoul 04763, Korea

Correspondence to: ^*E-mail: sjjeong@katech.re.kr

Copyright Ⓒ 2020 KSAE / 172-05
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.

Abstract

There is a worldwide understanding that hydrogen has a great potential as the fuel of the future. In addition to the challenge of developing appropriate hydrogen propulsion systems, however, the development of hydrogen storage systems is another big issue. The stored liquid hydrogen must be kept at a temperature of about 20 K. As such, the space between the outer jacket and the inner tank is mainly used for thermal insulation. The permanent heat input during the time when the vehicle is not used leads to pressure and temperature increases in the hydrogen fuel. This study thus focused on the development of a three-dimensional CFD model of liquefied hydrogen storage systems in view of boil-off management for controlled evaporation, pressurization in ullage, the flow characteristics of liquid and vapor, thermal stratification, and the evaporation characteristics on the free surface. Two-phase CFD-compressible VOF models with a Ranz-Marshall interfacial model using a customized in-house version of AVL, Fire®, for liquid hydrogen tank self-pressurization and pressure control were used to show the impact of interfacial and vapor phase turbulence on the evolution of the pressure and temperature in cryogenic storage tanks. The results show that the present CFD model has good adaptability in the prediction of pressurization behaviors, and is a useful tool for the design and optimization of a pressurization system.

Keywords:

Liquified hydrogen tank, Cryogenics, CFD, VOF(Volume of Fluid), Free surface, Boil-off gas(BOG), Evaporation

키워드:

액화 수소탱크, 냉동공학, 전산유체역학, 유체체적법, 자유표면, 증발가스, 증발

1. 서 론

수소경제 실현을 위한 핵심 솔루션은 저장 및 이송 효율성이 좋고 안전성을 확보하는 수소저장기술이라고 할 수 있다. 이중 액화수소는 기체 수소대비 약 800배의 저장밀도와 10배의 이송 경제성을 가지고 있으므로 자동차 및 선박과 같이 장시간 고출력으로 운용하여야 하는 장치에 매우 유용하다. 따라서 미래의 무공해 대체에너지원인 액화수소를 연료로 사용하는 자동차와 같은 이송장치 개발에 있어서 가장 중요한 기술적인 문제는 극저온 상태의 액화수소를 효율적으로 저장하고 연료의 사용을 위해 손쉽게 기체형태의 수소로 추출할 수 있는 저장용기의 개발이다. 액화수소는 상압에서 20 K로 유지되는 극저온 유체로 외부로 부터의 열 유입에 의한 기화손실을 최소화할 수 있는 초단열기술의 개발이 선행되어야 한다. 저장용기의 단열을 위해서는 현재 여러 가지 방법이 복합적으로 사용되고 있으며, 이러한 방법들을 통하여 외부로부터의 열유입을 효과적으로 차단할 수 있는 것으로 알려져 있다. 그러나 액화수소 탱크 내에는 수소연료의 충전관 및 지지대 그리고 배출관등이 설치되어 있으므로 이러한 구성품을 통한 열유입이 매우커서 액화수소의 저장효율이 크게 감소되는 문제점이 있다.

이렇게 용기 내로 침투한 열로 인하여 액화수소는 증발하게 되고 이러한 증발가스를 BOG라고 부른다. BOG의 다량 발생으로 인하여 탱크내의 압력이 증가하여 폭발이 일어날 위험성이 있으므로 BOG가스량을 최소화하는 방법을 개발하는 것이 매우 중요하다. 이러한 우수한 단열효과와 BOG Free 기술은 2004년에 BMW Group에서 수소연료용 ICE에 적용하여 Hydrogen 7-Series에 적용하여 그 가능성을 보인 바 있다.¹⁾ 액화수소연료 차량이 사용되지 않을 때 용기 내로의 열의 유입량은 증발로 인하여 용기 내의 압력과 온도를 상승시키기 때문에 안전을 위하여 대략 5 bar 이상 압력이 상승하면 BOG밸브를 통하여 가스를 외부로 방출시키게 되어있다.

이러한 액화수소저장용기에 대한 단열성능에 관한 연구는 VOF와 같은 자유표면 모델링기법이 개발되면서 최근들어 수치해석 모델링에 관하여 집중적으로 이루어지고 있다.^2-4) 그러나 이러한 액화수소 저장용기 개발에 관한 원천기술은 선진 7개국만이 보유하고 있는 실정이고 따라서 국내에서도 이와 관련된 연구가 절실하다고 할 수 있겠다.

그러므로, 본 연구에서는 이러한 탱크 내의 열유입으로 인한 다양한 물리적 현상을 규명하고 예측하기 위하여 액화수소 저장기의 단열성능, 기화손실 및 내부 압력상승 예측을 위하여 극저온 열유동해석 모델을 개발하였다. 이 모델은 저장용기 내 자유표면에서의 증발 및 응축을 고려하여 외부 열 침투에 의한 액화수소 기화손실을 최소화하고 저장효율을 극대화하기 위한 최적 단열 설계안을 도출하는데 큰 역할을 할 것으로 기대된다.

2. 해석모델개발

2.1 액화수소탱크 내의 열물성 거동

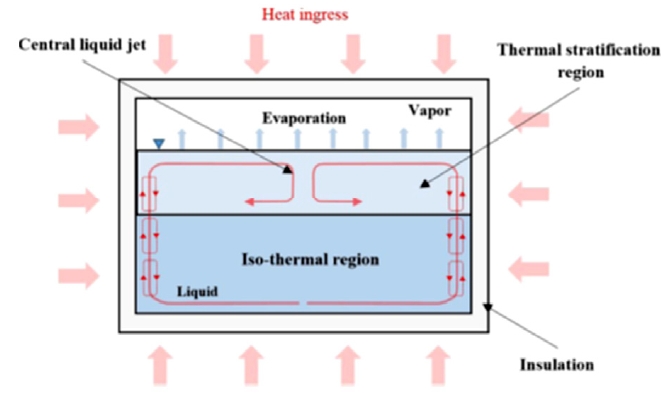
상온으로부터 극저온 액체를 저장하고 있는 탱크 내로 유입되는 열유입의 종류와 경로는 일반 열전달의 형태인 전도, 대류 및 복사로 분류할 수 있다. 본 연구에서는 전도 열손실과 대류열손실을 고려하여 모델링하였다. 극저온 액화수소용기 내의 열침투로 인한 대류열손실의 주요 물리적현상은 Fig. 1에 나타내었듯이, 탱크 내부의 액화수소가 외부 열유입에 의하여 탱크 벽 측에서 자연대류 현상으로 인한 액체의 유동이 발생하고, 액체영역 상단으로 이동된 액채는 기체와 액체와의 경계면에서 액체-기체 사이의 증발이 일어나며, 증발된 찬 기체는 상단의목부분으로 자연대류 하면서 추가적 증발손실이 발생한다. 따라서 모델링을 위한 주요 현상은 액상내의 부력으로 인한 자유표면근처에서의 열적성층화와 이에 따른 기상(Ullage)으로의 증발과 부력으로 인한 난류유동, 그리고 탱크 내부 벽면에서의 공역열전달(Conjugate heat transfer)이다.

Fig. 1

Self-pressurization subject to a liquid and vapor heat flux4)

2.2 지배방정식 및 수치모델

본 연구에서는 액화용기의 유동을 3차원 비정상 압축성 난류유동으로 고려하였으며, 액상과 기상의 경계면에서의 증발과 응축을 해석하기 위하여, 유체체적법(VOF: Volume of Fluid)⁵⁾을 사용하였다. 이 모델은 격자 크기에 비해 큰 입자들을 가지고 있는 비혼합유체의 액상과 기상의 경계면을 추적하는 수치기법이다. 이 수치기법은 액상과 기상 역역이 모두 같은 운동량 및 에너지 방정식을 사용할 수 있다. 즉 각 상에서 같은 압력, 온도, 속도장을 공유할 수 있어 매우 경제적이며, 많은 연구자들이 사용하여, 해석 정확도가 입증된 바 있다. 본 연구에서는 수소액화탱크 내부의 액상과 기상의 연속상을 계산하기 위해 동일한 지배방정식들이 액상과 기상의 체적분율을 계산하는데 사용되며, 이는 밀도와 점성에 적용되어 각 상을 연계시킨다.

본 연구에서 고려한 3차원 비정상 압축성 비혼합 유체에 대한 질량, 운동량 및 에너지보존방정식은 아래와 같다.

∂ ρ ∂ t + ∇ ⋅ ρ u = 0

(1)

∂ ∂ t ρ u j + ∂ ∂ x j ρ u i u j = - ∂ P ∂ x j + μ e f f ∂ u i ∂ x j + ∂ u j ∂ u i + ρ g i + f σ

(2)

여기서,

∂ (ρ E) ∂ t + ∇ ⋅ ν ρ E + P = ∇ ⋅ k e f f ∇ T + S ˙ q, c - S ˙ q, e

(3)

기상과 액상 경계면의 추적은 각 상의 체적분율(α)에 대한 아래의 연속방정식을 사용하여 수행된다.

∂ α ∂ t + u i ∂ α ∂ x i = - S ˙ m, e + S ˙ m, c

(4)

즉, 계산 셀이 전부 증기로 채워져 있으면, α = 1이고 반대의 경우는 영이다. 상 경계면에서는 0≤α≤1의 값을 가지게 된다. 위의 식 (3)의 우측 항에 포함되어 있는 fg는 표면장력이며 식 (4)의 $S ˙ m, e$ 와 $S ˙ m, c$ 는 액체 표면에서의 증발율과 응축률이다. 각 계산셀에서의 액상과 기상의 혼합 밀도 및 동점성계수는 아래의 방정식으로 표현될 수 있다.

ρ = α g ρ g + 1 - α g ρ l

(5)

μ = α g μ g + 1 - α g μ l

(6)

VOF 모델에서는 에너지방정식에 포함되어 있는 에너지, E 와 온도, T 는 아래와 같이 질량평균을 하여 각 셀에서 사용한다.

E = α g ρ g E g + α l ρ l E l α g ρ g + α l ρ l

(7)

여기서, E = c_PT 이며, 에너지방정식에 포함된 $S ˙ q, e$ 는 액체의 증발잠열에 의한 에너지 생성항이며, $S ˙ q, c$ 증기의 응축에 의한 에너지 생성항이다.

액상표면에서의 증발 시 나타나는 증발잠열은 포화온도에서 증기와 액체의 엔탈피 차이로 계산되며, 아래식과 같이 표현된다.

h l a t = h υ T s a t - h l (T s a t)

(8)

여기서, h_υ (T_sat) = h_o (T_sat) + C_pυ (T_sat−T_oυ)이고, h_l (T_sat) = h_ol + C_pl(T_sat−T_0l)이며, T_0l과 T_0υ는 증기와 액체의 기준상태의 온도를 나타낸다. 해의 안정성을 확보하기 위해 h_0υ 또는 h_0l은 영으로 설정하고, 다른 한 개는 적절한 값을 입력하였다. VOF 모델에서는 경계면에 포함되어 있는 계산셀에 작용하는 체적항으로 표면장력에 계산되어진다. 표면장력을 계산하기 위해 CSF(Continuum Surface Force) 모델을 사용한다. 액상과 기상의 경계면에서는 큰 압력비약이 형성되어지며, 평형상태에서는 이 압력비약으로 인한 압력구배는 운동량방정식에 포함되어져 있는 부력항과 같은 크기여야 한다. 따라서 상 경계면에서 현저하게 나타나는 압력구배에 의한 힘은 아래의 식으로 표현되어진다.

f σ = - σ ∇ ⋅ ∇ α α ∇ α

(9)

운동량방정식 (2)에 포함되어져 있는 유효동점성계수, μ_eff는 아래의 식으로 표현되어지며, 식에 포함되어져 있는 난류점성계수, μ_t를 계산하기 위하여 본 연구에서는 k−ξ−f 난류모델⁶⁾을 사용하였다. 이 모델은 기존의 k-ε계열의 난류모델에 비해 열전달, 저 레이놀즈에서의 표면마찰, 역압력구배 및 재순환영역에서 높은 예측 정확도를 보유하고 있는 V2F모델⁹⁾의 수치적 경직성을 완화하기 위하여 개발된 모델¹⁰⁾이다. 본 모델은 저 레이놀즈 모델과 같은 특성을 갖지만 이것과는 달리 벽면 근처에서도 사용이 가능하기 때문에 벽함수가 도입될 필요가 없다. 대신 벽으로부터의 난류에너지 수송을 위한 υ²을 도입하여 타원형 이완 방정식으로 벽근처의 와점성 감쇠효과를 효과적으로 표현한다. 따라서 본 연구의 경우처럼 벽으로 둘러싸여져 있는 저 레이놀즈 유동 및 열전달에 탁월한 예측성능을 보유하고 있다. 본 연구의 경우, 유동이 1.13×10¹³≤Ra≤5.65×10¹³인 부력에 의존하는 저속 난류 자연대류 영역이므로 고 레이놀즈 RANS 난류모델의 예측정확도가 떨어져 벽함수를 적용할 수 없다.

많은 선행연구^7,8)도 극저온유체 용기내의 벽면과 유체와의 열전달과 유체의 부력에 의한 자연대류 현상을 정확하게 계산하기 위하여 벽함수를 쓰지않고 층류저층과 이행층(Buffer layer)을 감쇠 함수(Damping function)에 의해 직접 계산할 수 있는 low-Re k-ε모델 사용을 추천하고 있다.

계산된 난류점성계수는 아래식과 같이 사용된다.

μ e f f = μ + μ t

(10)

상 경계면에서의 증발과 응축을 고려하기 위해서 식 (11)과 같은 농도방정식을 각 상에 대해서 계산하였다.

∂ ∂ t ρ X m + ∂ ∂ x i ρ u i X m = - ρ D e f f ∇ 2 X m - S ˙ m, c + S ˙ m, e m = 1 : υ a p o r, m = 2 : l i q u i d

(11)

윗 식에 포함된 $S ˙ m, c$ 는 응축에 의한, $S ˙ m, e$ 는 증발에 의한 물질 생성항을 의미하며, 단위표면적당 증발율(kg/sm²)과 응축율(kg/sm²)은 Ranz-Marshall⁶⁾모델을 적용하여 계산하였다. 이 모델은 기존에 주로 사용되었던 Schrage 방정식²⁾의 약점인 적응계수(Accommodation factor)의 보정이 필요 없다는 장점이 있다. 본 연구에서는 해석 모델 개발을 위하여 사용한 프로그램은 AVL(社)의 Fire Classic code⁶⁾를 이용하였으며 본 연구를 위하여 자유표면에서의 증발 및 응축모델을 프로그래밍하고 압력과 온도에 따른 수소의 물성치¹¹⁾를 데이터베이스화한 Customized version code이다. 또한 액화수소의 증발에 의한 압력변동에 따른 포화온도변화를 고려하기 위하여 별도의 테이블을 작성하여 사용하였다.

2.3 해석 대상 액화 수소 용기

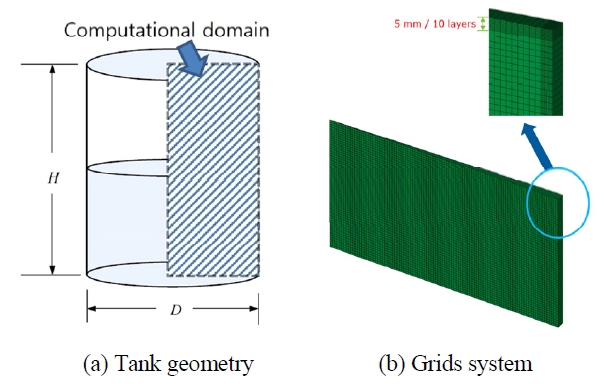
본 연구에서 고려한 모델³⁾은 Fig. 2(a)에서 나타내었듯이, 원통형이며 액상과 기상은 각각 50 %로 설정하였다. 액화수소 용기 모델은 축대칭이므로 2D으로 고려하였으며 직경(D)은 0.5 m이고 높이(H)는 1 m인 약 200 liter 부피의 원통이며 계산영역은 약 40,000개의 격자로 구성하였다. 격자수는 20,000~60,000개의 셀을 사용하여 격자의존도 계산을 수행하여 벽면에서의 y+값이 1에 접근할 수 있는 최소 셀(40,000개)을 사용하였으며 이를 위하여 Fig. 2(b)에서와 같이 벽면에 매우 조밀한 격자밀도를 형성시켰다.

Fig. 2

Schematic diagram of LH2 tank

2.4 경계 및 수치 조건

본 해석은 탱크 표면으로의 열침투가 일어나기 전에 준포화상태로 가정하여 기상에서의 초기압력을 대기압(101.32 kPa)으로 설정하였고, 액체에서의 압력은 밀도와 높이로 계산하여 설정하였다. 초기온도는 액상 및 기상 모두 1 atm에서의 포화온도인 20.268 K로 계산하였다. 벽면에서의 경계조건은 3가지 일정한 열유속(50 W/m², 150 W/m², 250 W/m²)을 탱크의 외곽 표면에 지정하였고 점착조건으로 설정하였다. 탱크의 상면과 하면은 각각 단열조건으로 지정하였다. 상세 경계조건은 Table 1에 정리하여 나타내었다.

Table 1

Details of boundary conditions

본 연구에서 사용된 운동량방정식의 대류항 차분법은 2차 정도를 지닌 MINMOD⁶⁾를 사용하였고, 연속방정식은 중앙차분법을, 난류이송방정식과 에너지방정식은 상류차분법을 적용하여 계산하였다. 그 밖의 하향이완계수와 수렴판정 조건은 Table 2에 정리하여 나타내었다.

Table 2

Details of numerical control parameters

3. 해석결과

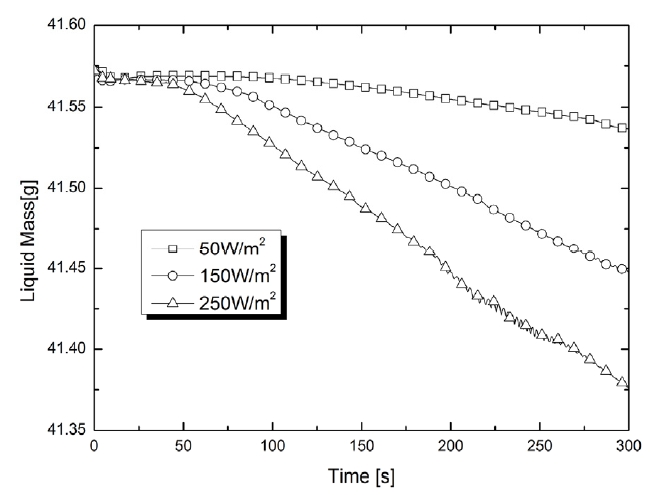
본 연구에서 개발된 해석모델의 예측성능 검증을 위하여 Fig. 3에 측면벽면에서의 3가지 열유속이 가해질 경우의 탱크 내의 증발에 의한 압력상승효과를 시간에 따라 나타내었으며 그 결과를 선행연구³⁾의 해석결과와 비교를 하였다. 비교결과, 증발에 의한 압력상승이 이루어지기 까지는 벽면으로 유입되는 열유속에 의한 부력이 더운 액화수소를 자유표면까지 상승시켜 자유표면 아래에 열적 성층화가 생성되기까지 일정한 시간이 걸리는데 본 해석결과를 보면 이러한 탱크내의 초기의 대류냉각과 부력의 상호연계에 의한 증발지연효과와 액화수소 증발 촉발 후 이에 따른 압력상승을 시간에 따라 잘 나타내고 있으며 그 결과역시 기존결과³⁾와 잘 일치하고 있음을 확인할 수 있다. 또한 측면 유입 열유속량의 증가에 따라 증발지연시간이 감소하는 현상과 Fig. 4에서 확인할 수 있듯이, 시간이 경과함에 따라 액화수소의 질량이 자유표면으로부터 증발율이 급격히 증가하는 현상을 잘 표현해주고 있음을 확인할 수 있다.

Fig. 3

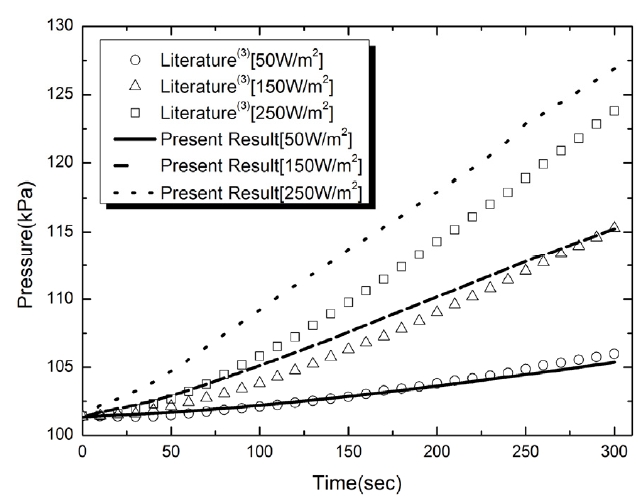
Prediction for evolution of pressure for the self-pressurization of the 50 % filled tank subjected to various sidewall heat flux: comparison of predictions against3)

Fig. 4

Comparison of liquid mass amounts with time for various uniform wall heat flux

그러나 측면 열유속이 커지는 250 W/m²의 경우는 기존 연구결과³⁾와 다른 경우에 비해 큰 차이를 보이고 있다. Altac¹²⁾의 연구결과에 의하면, 본연구와 유사한 정사각형 밀폐공간에서 양쪽 측면에 온도차를 주어 계산했을 경우에 표준 k-ε난류모델을 벽함수와 함께 사용한 해석결과는 Nu수를 과소평가하고 있음을 보고하였다. 따라서 표준 k-ε난류모델을 벽함수와 같이 사용한 기존결과³⁾는 벽면으로부터의 열유속이 자유표면 아래의 열성층화를 과소평가하여 증발율을 낮게 예측할 가능성이 있다. 이에 비해 본 연구의 경우는 벽함수를 사용하지 않고 벽근처에서의 와점성의 계산을 υ²방정식을 사용하여 이 영역에서의 속도변동의 비등방성효과를 효과적으로 계산할 수 있으므로 강한 부력이 지배적인 유동에서 정확한 예측성능을 기대할 수 있다.¹³⁾ 그러나 V2F모델 역시 부력이 지배적인 자연대류 문제에서 부력에 의한 벽근처에서의 불균일한 벽전단응력의 분포를 효과적으로 반영할 수 있는지에 대한 의문이 제기되고 있으므로¹⁴⁾ 향후 이와 관련된 실험적 검증과 상세한 모델평가가 이루어져야 한다고 생각된다.

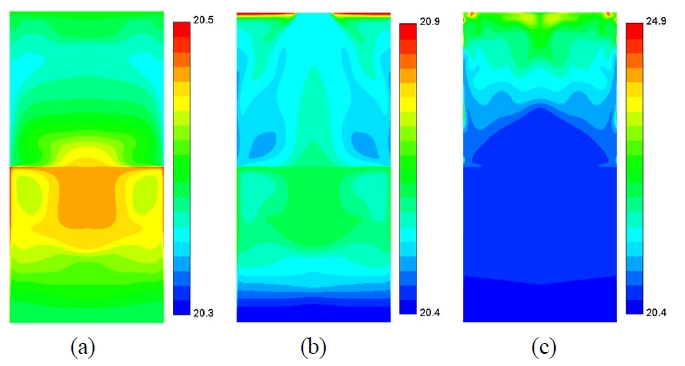
Fig. 5에 벽면가열 후 100초에서의 액상과 기상에서의 온도분포를 열유속 별로 나타내었다. 그림에서 볼 수 있듯이 자유경계면 아래에 열적 성층화가 형성되어져 있음을 알 수 있고 이로 인한 증발이 이루어진다. Fig. 5(a)의 경우, 액상에서 벽면으로부터의 열유입 되어 측면 벽근처에 큰 온도구배가 형성됨과 동시에 부력을 발생시켜 수직방향으로 엔탈피 이송이 시작되어 자유표면근처에 강한 온도구배가 형성되기 시작함을 볼 수 있다. Fig. 5(b)에서 볼 수 있듯이, 유입 열유속이 증가함에 따라 액상 내에 축방향으로 큰 열성층화가 이루어지고 있음을 볼 수 있고 기상의 경우는 중심축을 기준으로 반경방향으로 자연대류에 의한 큰 온도구배가 형성되어 있을 확인 할 수 있다. 특히 자유표면에서 증발된 수소가스가 벽면을 타고 상향제트류를 형성하면서 상면부에서 정체되면서 열 축적이 이루어져 상면부에 최고 온도가 분포되어 있음을 볼 수 있다. 벽면으로 열유입이 더욱 증가하면 Fig. 3(c)에서 볼 수 있듯이, 대류와 전도에 의한 에너지 평형이 이루어져서 자유표면의 온도가 더욱 상승할 뿐만 아니라 이로 인하여 열성층화가 형성되기 전에 증발이 일어나고 있음을 알 수 있다.

Fig. 5

Temperature(K) contours for three different heat fluxes after 100 s : (a) 50, (b) 150, (c) 250 W/m2

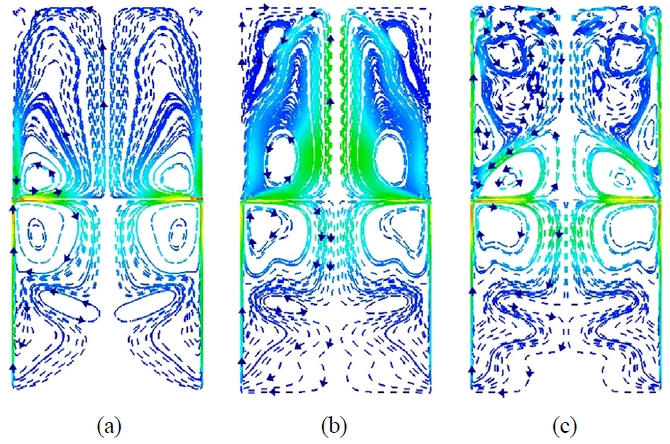
Fig. 6에 100초에서의 3가지 열유속에 대한 유선을 액상과 기상에서 동시에 나타내었다. 액상의 경우, 측벽으로부터 전도되는 열이 벽근처의 열경계층 내로 전달되어 일부가 유체를 팽창시켜 부력에 의해 상향 제트류를 형성하여 위쪽으로 흐르며 자유표면 근처에서 냉각되어 원통 중심축으로 이동하면서 밀도 상승으로 인하여 하강하며 한쌍의 와류를 형성하고 있다. 이 때 벽면으로 열유속의 과도한 유입으로 인하여 충분히 냉각되지 못한 하강류가 2차 와류를 형성함을 볼 수 있다. 벽면에서 제트류로 인하여 매우 큰 속도구배가 형성되어 있고 이는 자유표면에서 빠른 흐름을 유도하여 증발을 가속시키고 있다. 자유표면에서 증발된 기체상태의 수소는 액체표면에서 가열되면서 중심축으로 이동하며 액화수소는 자유표면 중심부에서 가장 높은 온도를 형성하므로 일부는 와류쪽으로 이동하고 일부는 기화되어 이후 중심축을 타고 상승하여 상면부에서 냉각되어 양쪽 벽면을 타고 제트류를 형성하여 자유표면으로 내려온다. 벽면에서 하향제트류가 발생하는 이유는 열경계층 보다 와류가 발생하는 영역의 온도가 높기 때문이다. 그러므로 기상에서도 한쌍의 와류가 형성되고 있다. 그러나 벽면으로부터 유입 열유속이 증가하면 Fig. 6(b)에서 볼 수 있듯이 상면부에서의 냉각이 충분히 이루어지지 않아 2차 와류가 형성되어 있으며 1차 와류의 세기도 더욱 발달되어져 있음을 알 수 있다. 또한 액상의 경우도 자유표면에서 더욱 활발한 증발이 일어나므로 잠열로 인한 대류냉각이 강해져 중심축에서 보다 강한 하향유동이 존재하고 따라서 Fig. 5(b)에서 볼 수 있듯이 축방향의 큰 온도구배를 형성한다. 벽면 유입 열유속이 증가하는 Fig. 6(c)의 경우는 액체의 평균온도가 상승하고 자유표면에서의 활발한 증발로 인하여 많은 높은 온도의 기체가 냉각되지 못하고 상면부에 정체되어 있다. 따라서 상층부의 많은 열축적으로 인하여 기체들이 작은 여러 개의 와류를 형성하며 정체되어 있어 그 아래쪽에 매우 축소된 1차 와류가 형성되어져 있음을 알 수 있다.

Fig. 6

Streamlines for three different heat fluxes after 100 s : (a) 50, (b) 150, (c) 250 W/m2

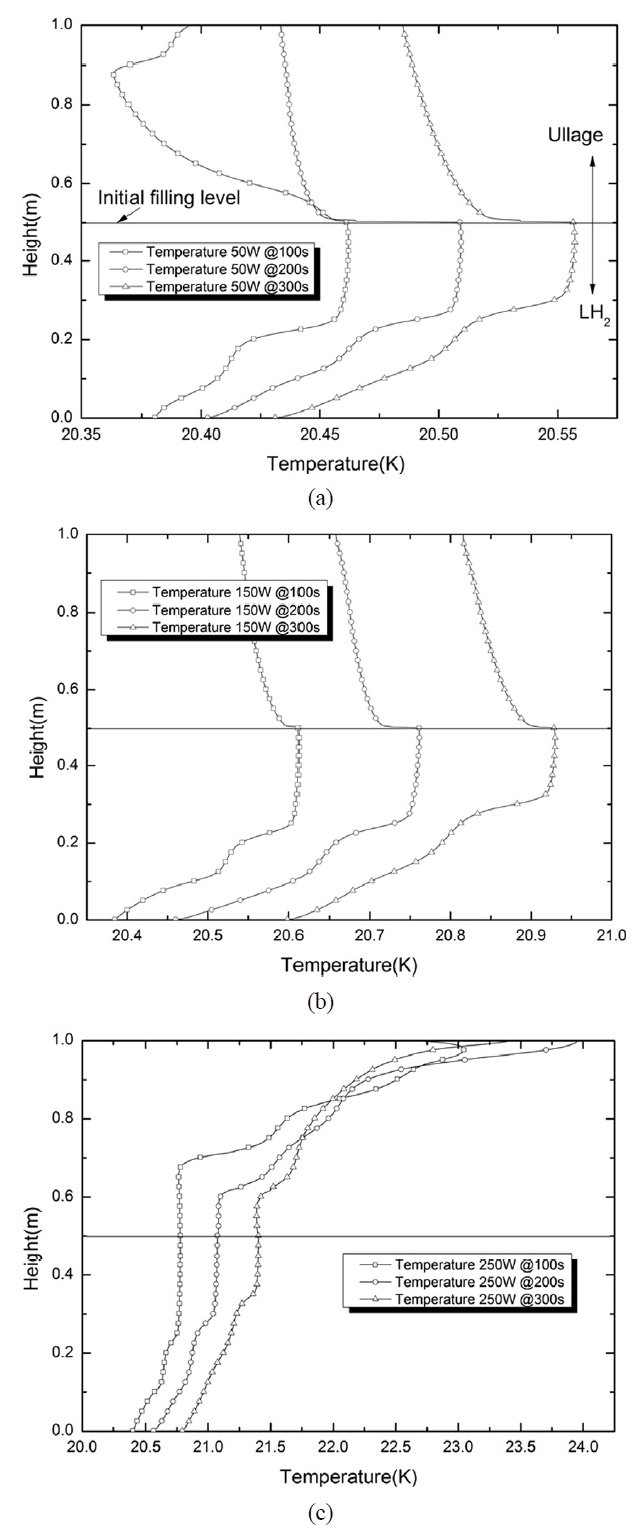
Fig. 7에 각 유입 열유속에 대하여 시간별 중심축에서의 축방향 온도분포를 나타내었다. 열경계층으로 열유입이 작은 Fig. 7(a)의 경우, 자유표면에서 증발이 미미하게 일어나며 냉각효과가 미미하여 온도구배가 미미하게 형성되다가 보다 하향유동이 일어나며 냉각되어 큰 온도구배를 형성하고 있다. 기체영역은 증발수소의 양이 미미하여 초기에는 자유표면에서 큰 온도구배를 보이며 역구배를 형성하다 점차 증발수소량이 증가하면서 완화됨을 볼 수 있다. 열유입이 점차 증가하면서 Fig. 7(b)에서 볼 수 있듯이, 자유표면으로부터 높은 온도의 충분한 증발가스가 상향류를 형성하므로 자유표면 근처를 제외하고 Fig. 7(a)에 비하여 온도구배가 매우 완화되어 있음을 확인할 수 있다. 액체의 경우는 중앙부 자유표면 아래에 최고 온도분포가 형성되어져 있으며 하면부에 접근할수록 냉각에 의한 온도구배를 확인할 수 있다. 더욱 열유입이 증가하는 Fig. 7(c)의 경우는 증발 가스량이 과도하게 생성되어 중심축에서 상향이동하면서 상면부에 높은 엔탈피를 가진 가스의 정체되는 영역이 시간이 지나면서 넓어지며 큰 온도구배를 형성하며 이 영역은 시간이 지남에 따라 확대되고 있음을 볼 수 있다. 액체영역도 자유표면에서의 활발한 증발이 하향류를 타고 강하게 흐르면서 점차 냉각된다. 시간이 흐르면서 증가하는 증발잠열로 인하여 냉각영역이 증가하고 있음을 확인할 수 있다. 이와 같은 결과들로부터 온도분포는 Fig. 5와 Fig. 6에서 볼 수 있듯이 유동분포에 강하게 연계되어 있음을 알 수 있다.

Fig. 7

Comparison of axial temperature profiles at centerline for various times: (a) 50, (b) 150, (c) 250 W/m2

4. 결 론

본 연구에서는 액화수소연료를 효율적으로 사용하기 위한 극저온 수소액화기의 외부로부터의 열 침투에 의한 기화손실 및 내부 압력상승을 예측하기 위한 3차원 극저온 열해석 모델을 개발하여 외부 열유속 변화에 따른 탱크 내 물리적 변화를 연구하였으며 그 결과는 아래와 같다.

1) 자유표면해석을 위하여 VOF모델을 적용하였으며 기･액 상변화해석을 위하여 Ranz-Marshall⁶⁾모델을 사용하였다. 해석조건이 H/D < Ra^1/4인 조건에 해당하는 경계층영역(Boundary Layer Regime)¹⁵⁾이고 따라서 정체 및 낮은 레이놀즈수 유동과 열성층화가 주된 특성이므로 이를 모사할 수 있는 k−ξ−f 난류모델을 적용하였다. 개발된 해석모델을 검증하기 위하여 기존 연구결과³⁾를 이용하였으며 외부 열유속 유입에 따른 탱크 내부의 압력상승효과 및 상변화에 따른 내부 유체거동을 매우 신뢰성 있게 예측하였다.
2) 탱크 내 기상과 액상 수소의 자연대류현상 및 이에 따른 열적 성층화 과정을 매우 잘 표현할 수 있었으며 이에 따른 탱크 내 가압현상을 물리적으로 타당하게 예측할 수 있었다.
3) 액화수소의 경우, 탱크 벽면으로부터의 열유입으로 인한 벽근처에서의 큰 온도구배 형성과 부력에 의한 수직방향으로의 엔탈피 이송에 기인하는 자유표면근처의 강한 온도구배가 형성을 잘 표현하였다. 이로 인한 증발가스는 중심축을 타고 상승하여 상면부에서 냉각되어 양쪽 벽면을 타고 제트류를 형성하여 자유표면으로 내려오는 하향제트류가 발생함을 확인하였다. 유입 열유속이 증가하면, 자유표면에서의 활발한 증발로 인하여 상면부에서의 불충분한 냉각이 발생하고 따라서 와류의 세기와 생성 개수가 증가함을 알 수 있었다. 액상영역도 자유표면에서의 충분한 냉각으로 인하여 축방향 온도구배가 완화되고 있음을 확인하였다.
4) 향후 본 연구에서 개발된 해석모델은 액화수소탱크 내의 증발가스 억제 및 건전성 설계 및 최적화에 유용하게 이용될 수 있을 것으로 사료된다.

Nomenclature


D :	diffusivity
g :	gravitational acceleration
h :	heat transfer coefficient
k :	conductivity
υ² :	wall normal fluctuations
D :	diameter of tank or diffusivity
H :	height of tank
P :	pressure
t :	time
x :	position in space
y+ :	dimensionless normal distance from wall
ρ :	density
μ :	viscosity
ν :	kinematic viscosity
c_p :	specific heat
χ :	species mass fraction
▽ :	gradient
Ra :	rayleigh number

Subscripts


air :	air
eff :	effective
g :	gas
i,j :	coordinate
ℓ :	liquid
s :	surface
sat :	saturation
v :	vapour
o :	reference

Acknowledgments

본 연구는 중소벤처기업부의 창업성장기술개발사업의 일환으로 수행되었습니다. 프로그램 사용 및 개발에 많은 지원을 해주신 AVL 관계자 여러분께 진심으로 감사드립니다.

References

F. Amasedar and G. Krainz, “Liquid Hydrogen Storage Systems Developed and Manufactured for the First Time for Customer Cars,” SAE 2006-01-0432, 2006. [https://doi.org/10.4271/2006-01-0432]
M. Kassemi and O. Kartuzova, “Effect of Interfacial Turbulence and Accomodation Coefficient on CFD Predictions of Pressurization and Pressure Control in Cryogenic Storage Tank,” Cryogenics, Vol.74, pp.138-153, 2016. [https://doi.org/10.1016/j.cryogenics.2015.10.018]
B. Sunden and J. Fu, Heat Transfer in Aerospace Applications, Academic Press, Cambridge, Massachusetts, pp.71-87, 2016. [https://doi.org/10.1016/B978-0-12-809760-1.00005-3]
Z. Liu and Y. Li, “Thermal Physical Performance in Liquid Hydrogen Tank under Constant Wall Temperature,” Renewable Energy, Vol.130, pp.601-612, 2019. [https://doi.org/10.1016/j.renene.2018.02.023]
S. Hardt and F. Wondra, “Evaporation Model for Interfacial Flows Based on a Continuum-field Representation of the Source Terms,” Journal of Computational Physics, Vol.227, No.11, pp.5871-5895, 2008. [https://doi.org/10.1016/j.jcp.2008.02.020]
AVL FIRE^® Main Program User Manual Ver.2019.1, 2019.
L. Wang, Y. Li, C. Li and Z. Zhao, “CFD Investigation of Thermal and Pressurization Performance in LH₂ Tank during Discharge,” Cryogenics, Vol.57, pp.63-73, 2013. [https://doi.org/10.1016/j.cryogenics.2013.05.005]
L. Wang, Y. Li, Z. Zaho and Z. Liu, “Transient Thermal and Pressurization Performance of LO₂ Tank during Helium Pressurization combined with Outside Aerodynamic Heating,” International Journal of Heat and Mass Transfer, Vol.62, pp.263-271, 2013. [https://doi.org/10.1016/j.ijheatmasstransfer.2013.03.021]
P. A. Durbin, “Near-wall Turbulence Closure Modelling without “Damping Functions,”” Theoretical and Computational Fluid Dynamics, Vol.3, pp.1-13, 1991.
K. Hanjalic, M. Popovac and M. Hadziabdic, “A Robust Near-wall Elliptic-Relaxation Eddy-Viscosity Turbulence Model for CFD,” International Journal of Heat and Fluid Flow, Vol.25, Issue 6, pp.1047-1051, 2004. [https://doi.org/10.1016/j.ijheatfluidflow.2004.07.005]
NIST Chemistry WebBook, NIST Standard Reference Database Number 69, http://webbook.nist.gov/chemistry/, , 2019.
Z. Altac and N. Ugurlubilek, “Assessment of Turbulence Models in Natural Convection from Two-and three-dimensional Rectangular Enclosures,” International Journal of Thermal Sciences, Vol.107, pp.237-246, 2016. [https://doi.org/10.1016/j.ijthermalsci.2016.04.016]
R. E. Spall, A. Richards and D. M. McEligot, “An Assesment of k-w and v²-f Turbulence Models for Strongly Heated Internal Gas Flows,” Numerical Heat Transfer, Part A, Vol.46, pp.831-849, 2004. [https://doi.org/10.1080/104077890504032]
S. -Y. Kim, D. -H. Shin, C. -S. Kim, G. -C. Park and H. K. Cho, “Flow Visualization Experiment in a Two-side Wall Heated Rectangular Duct for Turbulence Model Assessment in Natural Convection Heat Transfer,” Nuclear Engineering and Design, Vol.341, pp.284-296, 2019. [https://doi.org/10.1016/j.nucengdes.2018.11.012]
A. Bejan, Convection Heat Transfer, 3rd Edn., John Wiley & Sons, Inc., Hoboken, New Jersey, pp.243-258, 2004.

Location	Conditions	Details
Sidewalls (Internal)	No slip	u_j = 0
Sidewalls (Outside)	Uniform wall heat flux (q_w=50, 150, 250 W/m²)	$- k ∂ T ∂ n = q w$
Top & Bottom surfaces	Adiabatic	$- k ∂ T ∂ n = 0$

	Parameter & Eqs.	Values
Under-relaxation	Momentum	0.1
	Turbulence	0.2
	Energy	0.6
	Scalar	0.8
	Pressure	0.05
Convergence - Criteria (Residual limit)	Momentum	0.0005
	Energy	5×10^-5
	Scalar(VOF)	0.0001
	Pressure	0.0001