MDPS 감속기용 웜기어의 정렬오차 및 웜휠 가공용 호브 제원이 치 접촉에 미치는 영향 연구

1. 서 론

MDPS^1,2)감속기용 웜기어의 형태는 원통형 웜과 장구형 웜휠의 조합인 싱글 인벨로핑 웜기어를 많이 사용하며, 웜의 치형은 ZI 치형을 사용한다. ZI 치형의 웜은 기하학적으로 헬리컬각이 매우 큰 인벌류트 헬리컬기어와 같으며 인벌류트 곡선에 대한 수식은 간단하고 잘 알려져 있기 때문에 치형의 3차원 모델을 얻기가 어렵지 않다. 그러나 웜휠은 ZI치형을 가지는 웜 또는 호브에 대한 공액 치형이므로, 정확한 치형 모델은 미분기하학을 이용한 수치해석을 통해 얻어야 하므로 그 과정이 다소 까다롭다. 이러한 이유로 장구형 웜휠을 사용하는 웜기어의 3차원 모델이나 접촉패턴은 상용 기어설계 소프트웨어들에서도 대부분 지원하지 않으며, 지원하더라도 근사적인 3차원 모델을 이용하기 때문에 정확한 접촉패턴을 기대하기는 어렵다. 기어의 접촉패턴은 서로 힘을 전달하는 기어 치면 사이의 맞물림이 적절한지의 여부를 판별할 수 있는 중요한 지표이기 때문에, 제품 제작 전에 이를 확인하는 것은 설계에서 매우 중요한 요소이다. 싱글 인벨로핑 웜기어의 접촉패턴은 웜휠 치면을 정면에서 봤을 때 치면 중앙에 비스듬히 분포하는 것이 이상적이다. 접촉패턴은 가공오차나 정렬오차에 따라 상하좌우로 이동하며 그 형상도 변하는데, 어떤 경우에는 치간섭 현상이 나타나서 모서리 접촉으로 이어지기도 한다. 또한 접촉패턴은 웜휠 가공용 호브의 증경량(Oversize)이나 호브의 줄 수에 의해서도 영향을 받는다. 따라서 이러한 설계변수 및 발생 가능한 정렬오차에 따른 접촉패턴의 변화를 확인하는 것은 웜기어 설계에 필수적이라 할 수 있다.

MDPS 감속기용 웜기어는 백래쉬가 없어야 하는데, 이를 위해 ARS(Anti-Rattle Spring)^1,2) 장치를 사용한다. ARS는 웜 샤프트의 한쪽 끝을 웜휠 쪽으로 계속 눌러주어 백래시가 없도록 해 주며 부하 변동이나 치두께 변화에 따라 웜과 웜휠의 중심거리가 변화하도록 해 준다. 중심거리의 변화는 웜기어의 정렬오차에 해당하며, 정렬오차는 접촉 패턴을 변화시킨다. 따라서 MDPS 감속기용 웜기어는 설계 시 중심거리오차를 고려한 접촉패턴 검토가 필요하다.

싱글 인벨로핑 웜기어의 치 접촉에 대한 연구는 몇몇 학자들에 의해 진행되어왔다. 일반화된 TCA(Tooth Contact Analysis)를 통한 전달오차(Transmission Error) 및 타원 접촉 패턴 계산에 대한 연구가 Litvin과 Kin³⁾에 의해 이루어졌다. Narayan 등⁴⁾은 가공 변수가 웜기어 구동 성능에 미치는 영향을 연구하였다. Fang과 Tsay^5,6)은 ZK웜과 ZN웜에 대하여 전달오차와 타원 접촉 패턴을 계산하고 축 정렬오차와 호브 증경량에 따른 접촉 패턴의 이동경로 변화를 연구하였다. 부하 시 치 변형에 의한 모서리 접촉을 방지하는 개선된 형상의 웜기어에 대한 연구가 Litvin 등⁷⁾에 의해 수행되었다. 개선된 웜기어는 위로 볼록한 포물선 형태의 전달오차 함수를 보여줬다. Simon^8,9)은 싱글 인벨로핑 웜기어에 LTCA(Loaded Tooth Contact Analysis)를 적용하는 방법을 제시하였는데, 타원 접촉을 계산하지 않고 잠재적 접촉선을 따라 웜과 웜휠 치면이 떨어진 거리를 이용하여 하중 분포를 계산하였다. 축 정렬오차, 호브 증경량 및 가공 장비 세팅이 부하 시 치 접촉에 미치는 영향도 Simon¹⁰⁾에 의해 연구되었다. 손종현과 박노길¹¹⁾은 치면간 최소 근접 거리를 이용하여 접촉 패턴을 예측하는 치면간격해석(Surface Separation Topology) 기법을 제시하고, 이를 이용하여 싱글 인벨로핑 웜기어에서 발생하는 기하학적 치 간섭 현상을 규명하였다. 또한 그 후속 연구로 웜휠 가공장비 세팅과 축 정렬오차가 기하학적 치 간섭에 어떤 영향을 미치는지 연구하였으며,¹²⁾ 높은 리드각을 가진 싱글 인벨로핑 웜기어의 치 접촉 시 웜과 웜휠 치면 사이의 양쪽 틈새를 비대칭형에서 대칭형으로 변화시키는 변형된 웜휠 호빙 기법¹³⁾을 제시한 바 있다.

싱글 인벨로핑 웜기어에 대한 지난 연구^3-13)들은 대부분 웜휠 가공용 호브의 증경량(Hob oversize)을 5 % 이내의 낮은 값으로 설정하여 수행되었다. 호브 증경량은 웜의 피치직경 대비 웜휠 가공용 호브의 피치직경이 얼마나 더 큰지를 나타낸다. 웜이 호브와 동일한 경우 호브 증경량이 0 %가 되는데, 이 경우 이론적으로는 선접촉이 일어나지만 축 정렬오차를 전혀 흡수할 수 없으며 호브의 재연삭(Re-shar_pening)으로 직경이 줄어들면 사용할 수 없기 때문에 실제로는 사용되지 않는다. 반대로 호브 증경량이 0 % 보다 큰 경우, 이론적으로 점접촉이 일어나며 실제로는 타원 형태의 면접촉을 하게 된다. 호브 증경량이 커질수록 접촉면적은 줄어들며, 상대적으로 흡수할 수 있는 정렬오차의 크기도 증가한다. 호브 증경량이 무한대로 커지면 싱글 인벨로핑 웜기어는 크로스헬리컬기어(Crossed helical gears)¹⁴⁾와 같게 되어 축 정렬오차에 치 접촉이 거의 영향을 받지 않지만 면압강도가 매우 약해진다. MDPS용 웜기어의 경우 일반적인 산업용 웜기어에 비해 상대적으로 축 정렬오차가 크게 발생하기 때문에 호브 증경량을 어느 수준 이상으로 크게 설정해야 치 접촉을 중앙에 유지시키고 치 간섭도 피할 수 있다. 그러나 과도하게 큰 호브 증경량은 면압강도를 떨어뜨리고 결과적으로 감속기의 크기를 증가시킨다. 호브의 줄 수는 일반적으로 웜의 줄 수와 같게 설정하지만, 경우에 따라 호브의 줄 수를 더 크게 설정하는 경우가 있다. 호브 증경량이 같더라도 호브의 줄 수가 바뀌면 접촉패턴이 변하며, 이러한 특성은 접촉패턴 최적화에 이용할 수 있다. 또한 MDPS용 웜기어는 높은 효율을 위해 웜의 리드각을 크게 설계하는데, 큰 리드각을 가지는 웜기어는 기하학적으로 치 간섭¹¹⁾이 잘 발생하며 호브 증경량 및 호브 줄 수는 치 간섭 여부와 직접적으로 관계되어있다. 따라서 주어진 정렬오차 조건에서 치 접촉을 치면 중앙에 유지시키고 치 간섭은 발생시키지 않는 최소의 호브 증경량과 적절한 호브 줄 수를 찾는 것은 MDPS용 웜기어 최적설계에 필수적이라 할 수 있다.

이 연구에서는 MDPS 감속기용 웜기어의 접촉패턴이 중심거리오차에 따라 어떻게 변화하는지를 살펴보고, 웜휠 가공용 호브의 증경량 및 줄 수가 여기에 어떤 영향을 미치는지를 분석하였다. 웜과 웜휠 치면간 접촉패턴의 계산은 미분기하학을 이용하여 웜과 웜휠 치면을 수학적으로 정의하고, 두 치면이 기구학적으로 접촉하여 구동할 때에 최대로 근접한 거리를 웜휠 치면 전체 범위에 대하여 계산하는 치면간격해석¹¹⁾ 기법을 이용하였다. 또한 치면간격해석 결과의 교차확인을 위하여, 웜과 웜휠 치면의 수학적 정의로부터 얻은 3차원 모델을 이용한 유한요소해석이 병행되었다.

2. 본 론

2.1 웜기어 치면의 수학적 표현

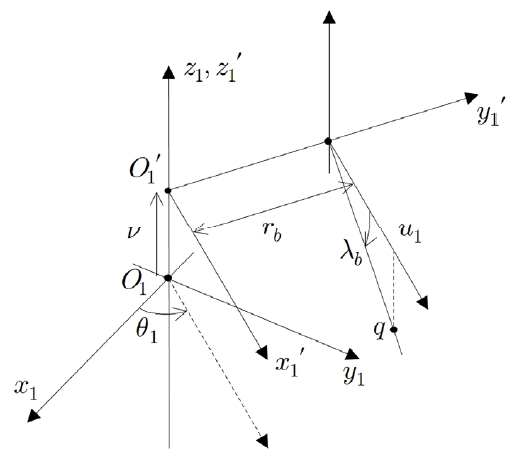
ZI 웜 또는 호브의 치면은 인벌류트 곡선이 스크류 운동할 때의 궤적과 같으며 이는 선직면(Ruled surface)이므로 직선의 스크류 운동으로도 나타낼 수 있다. Fig. 1은 웜 또는 호브 치면 상의 임의의 점 q를 보여준다. 점 O₁′을 원점으로 하는 좌표계 C₁′(x₁′, y₁′, z₁′) 상의 벡터 $$ \overrightarrow{O_1\text{'}q}$$는 다음과 같이 표현할 수 있다.

Fig. 1

An illustration of ZI worm surface

$\[ \overrightarrow{O_1\text{'}q}=\left[\begin{array}{c}{u}_1\\ r_b\\ -u_1\tan {\lambda }_b\end{array}\right] \]$

(1)

좌표계 C₁′(x₁′, y₁′, z₁′) 는 점 O₁을 원점으로 하는 좌표계 C1 (x₁, y₁, z₁) 에 대하여 z₁축 방향으로 ν만큼 진행하여 z₁축에 대하여 θ₁만큼 회전되어 있으므로, 벡터 $$ \nu =\frac{l{\theta }_1}{2\pi }$$는 좌표계 C₁ (x₁, y₁, z₁) 상에 다음과 같이 표현할 수 있다.

$\[ \overrightarrow{O_{1}q}=\left[\begin{array}{c}{u}_1\cos {\theta }_1-r_b\sin {\theta }_1\\ r_b\cos {\theta }_1+u_1\sin {\theta }_1\\ \nu -u_1\tan {\lambda }_b\end{array}\right] \]$

(2)

여기서, $$ \overrightarrow{O_{1}q}$$ 이다. 따라서 웜 또는 호브 치면은 벡터 $$ \nu =\frac{l{\theta }_1}{2\pi }$$의 직교좌표계 벡터성분에 상수성분 1을 추가하여 4×1 벡터 $$ \overrightarrow{r_1}$$으로 웜 고정좌표계 상에 다음과 같이 표현할 수 있다.

$\[ \overrightarrow{r_1}=\left[\begin{array}{c}{u}_1\cos {\theta }_1-r_b\sin {\theta }_1\\ r_b\cos {\theta }_1+u_1\sin {\theta }_1\\ \frac{l{\theta }_1}{2\pi }-u_1\tan {\lambda }_b\\ 1\end{array}\right] \]$

(3)

여기서, u₁ 과 θ₁은 웜 또는 호브 치면의 독립 매개변수이다. r_b는 기초원 반경, l은 리드, λ_b는 기초 리드각을 나타내는 상수이며, r_b = r_pcosα_t, l = 2πr_ptanλ, $$ {\lambda }_b={\tan }^{-1}\left(\frac{\tan \lambda }{\cos {\alpha }_t}\right)$$이고, $$ {\alpha }_t={\tan }^{-1}\left(\frac{\tan {\alpha }_n}{\sin \lambda }\right)$$이다. r_p는 피치반경, λ는 리드각, α_t는 축직각 압력각, α_n은 치직각 압력각이다. 호브의 증경량 OS는 호브의 피치원이 웜의 피치원보다 얼마나 큰지를 % 단위로 나타내는 설계변수이며, 호브의 피치반경 r_ph와 리드각 λ_h는 OS에 의해 다음과 같이 계산된다.

$\[ r_{ph}=r_{pw}(1+OS) \]$

(4)

$\[ {\lambda }_h={\sin }^{-1}\left(\frac{Z_h\sin {\lambda }_w}{Z_w(1+OS)}\right) \]$

(5)

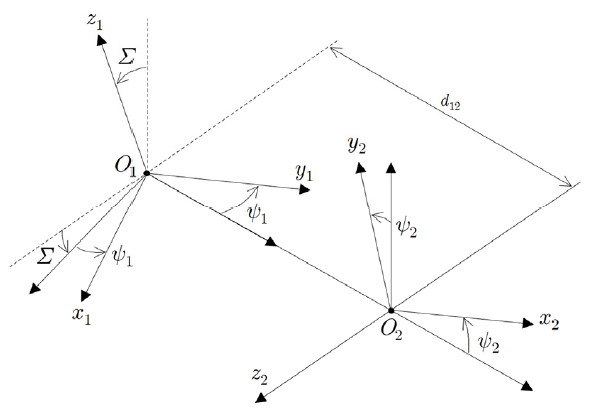
여기서, 아래첨자 w는 웜을, h는 호브를 나타낸다. Z_h는 호브의 줄 수, Z_w는 웜의 줄 수를 나타낸다. Fig. 2는 호브와 웜휠의 운동관계를 나타내며, 웜휠 고정좌표계에서 바라본 호브 치면은 다음과 같이 표현할 수 있다.

Fig. 2

Relation between coordinate systems of a hob and an enveloping worm wheel

$\[ \overrightarrow{r_2}=M_{21}\overrightarrow{r_1} \]$

(6)

여기서, M₂₁은 웜 고정좌표계에서 웜휠 고정좌표계로의 변환행렬이며 다음과 같이 표현할 수 있다.

$\[ M_{21}=M_{\psi 2}{M}_{par}{M}_{\Sigma }{M}_{\psi 1} \]$

(7)

여기서,

$$ \begin{array}{c}{M}_{\psi 2}=\left[\begin{array}{cccc}\cos {\psi }_2& \sin {\psi }_2& 0& 0\\ -\sin {\psi }_2& \cos {\psi }_2& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right], M_{par}=\left[\begin{array}{cccc}0& 1& 0& -d_{12}\\ 0& 0& 1& 0\\ 1& 0& 0& 0\\ 0& 0& 0& 1\end{array}\right], \\ M_{\Sigma }=\left[\begin{array}{cccc}\cos \Sigma & 0& \sin \Sigma & 0\\ 0& 1& 0& 0\\ -\sin \Sigma & 0& \cos \Sigma & 0\\ 0& 0& 0& 1\end{array}\right], M_{\psi 1}=\left[\begin{array}{cccc}\cos {\psi }_1& -\sin {\psi }_1& 0& 0\\ \sin {\psi }_1& \cos {\psi }_1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\end{array}$$

이고, $$ {\psi }_2=\frac{Z_1}{Z_2}{\psi }_1, \Sigma ={\lambda }_{\omega }-{\lambda }_h$$이다. Z₁은 웜 또는 호브의 줄 수, Z₂는 웜휠의 잇수, 그리고 d₁₂는 호빙 시 호브와 웜휠의 중심거리이다. 웜휠 고정좌표계에서 바라본 호브 치면 $$ \overrightarrow{r_2}$$는 3개의 독립매개변수 u₁, θ₁ 그리고 ψ₁를 가지며, 이는 무수한 호브 치면의 집합을 나타낸다. 호브 치면 집합의 포락면(Enveloping surface)에서 만족되어야할 필요조건이 호브 치면상 한 점에서의 법선벡터와 상대속도 벡터가 수직이어야 한다는 조건인데, 이를 물림방정식¹⁵⁾이라 하며 다음과 같이 미분기하학적으로 표현된다.

$\[ f_{mesh}\left(u_1,{\theta }_1,{\psi }_1\right)=\left(\frac{\partial {\overrightarrow{r_2}}^{\mathrm{*}}}{\partial u_1}\times \frac{\partial {\overrightarrow{r_2}}^{\mathrm{*}}}{\partial {\theta }_1}\right)\cdot \frac{\partial {\overrightarrow{r_2}}^{\mathrm{*}}}{\partial {\psi }_1}=0 \]$

(8)

여기서 $$ {\overrightarrow{r_2}}^{\mathrm{*}}$$는 4×1 벡터 $$ \overrightarrow{r_2}$$에서 마지막 행 성분을 제거한 3×1 벡터이다. 물림방정식으로 $$ \overrightarrow{r_2}$$의 독립매개변수 3개 중 1개가 종속매개변수가 되면 나머지 2개의 독립매개변수로 웜휠 치면을 나타낼 수 있다. Fig. 3은 식 (6)과 (8)을 이용하여 웜휠 치면 상의 3차원 좌표를 계산하는 코드 구조의 예를 보여준다. Loop 1은 호브와 웜휠의 위치를 정의하는 매개변수 ψ₁에 대한 반복문이고, Loop 1 내부에 호브 치면을 나타내는 매개변수 중 하나인 u₁에 대한 반복문 Loop 2가 있다. 벡터 $$ \overrightarrow{r_2}$$의 3차원 좌표 성분들을 계산하기 위해서는 u₁, θ₁ 그리고 ψ₁을 알아야 하는데, Loop 1과 Loop 2에서 ψ₁과 u₁이 각각 정해 졌으므로 Loop 2 내부의 A 부분에서 나머지 매개변수 θ₁을 물림방정식인 식 (8)을 이용하여 계산한다. 물림방정식은 음함수(Implicit function)의 형태로 나타나며 그 수식이 길고 복잡하기 때문에 양함수(Explicit function)의 형태로 변환이 어렵다. 따라서 ψ₁과 u₁을 물림방정식에 대입 후 이분법이나 뉴턴-랩슨 법 등의 수치해석을 이용하여 θ₁을 계산해야 한다. 그 후 Loop 2 안의 B 부분에서 $$ \overrightarrow{r_2}$$에 u₁, θ₁ 그리고 ψ₁을 대입하면 웜휠 치면 상 한 점의 3차원 좌표 성분이 계산된다. 이러한 방식으로 Loop 1과 Loop 2에서 ψ₁과 u₁의 범위를 적절히 선택하여 계산하면 웜휠 치면을 나타내는 3차원 좌표군을 얻을 수 있다.

Fig. 3

An illustration of calculation loops for obtaining coordinates on wheel surface

2.2 치면간격해석 및 유한요소해석 기법

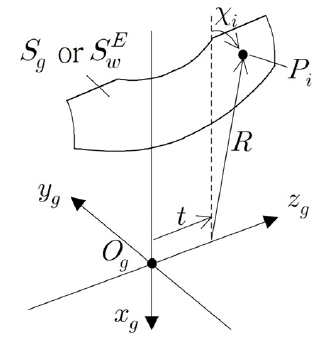
ZA, ZN 그리고 ZK 웜기어와는 달리, ZI 웜기어는 호브의 증경량이나 정렬오차와 무관하게 기구학적인 전달오차가 발생하지 않는다. 따라서 호브 증경량 OS를 0으로 설정하고 얻은 웜휠 치면은, 웜휠과 접촉하여 구동하는 웜 치면의 포락면과 같다. 웜 치면의 포락면을 $$ S_w^E$$, 호브 증경량이 양수인 실제 웜휠 치면을 S_g라 하면, S_g 상 임의의 지점과 $$ S_w^E$$ 사이의 간격은 웜 치면이 웜휠 치면에 최대로 근접했을 때의 간격을 나타낸다. 따라서 이 간격을 웜휠 치면 전체 범위에 대해 나타내면 웜기어 구동 시 웜휠 치면상에 나타나는 접촉패턴을 파악할 수 있다. 이 방법은 부하시의 탄성변형이 전혀 고려되지 않지만, 복잡한 치형을 가지는 싱글 인벨로핑 웜기어의 접촉패턴을 빠르게 확인하는데 효과적이다. 웜 치면의 포락면과 웜휠 치면 사이 간격은 Fig. 4와 같이 웜휠 반경 R과 웜휠 치폭방향 위치 t에 대하여 웜휠 축을 중심으로 한 호의 길이 ζ로 다음과 같이 계산하였다.

Fig. 4

An illustration of surface separation topology using a point Pi on SwE or Sg

$\[ \zeta =R\left({\mathcal{X}}_1-{\mathcal{X}}_2\right)=R\left({\mathit{tan}}^{-1}\left(\frac{y_{p_1}}{x_{p_1}}\right)-{\mathit{tan}}^{-1}\left(\frac{y_{p_2}}{x_{p_2}}\right)\right) \]$

(9)

여기서, P₁는 $$ S_w^E$$ 상의 점이고, P₂는 S_g상의 점이다. P_{i;(i = 1or 2)}의 좌표 (x_i, y_i, z_i)는 아래 조건을 만족해야 한다.

$\[ x_{p_i}^2+y_{p_i}^2=R^2 \]$

(10)

$\[ z_{p_i}=t \]$

(11)

식 (8), (10) 그리고 (11)은 독립매개변수 u₁, θ₁ 그리고 ψ₁ 에 대한 3개의 방정식이므로, 이를 수치해석으로 풀면 P_i의 좌표를 계산할 수 있으며 R, t 에 대한 ζ 값을 계산할 수 있다. ζ 값은 $$ S_w^E$$ 와 S_g의 치면간격을 나타내므로, 웜 및 웜휠 치면 유효범위에 대하여 계산된 ζ 값의 분포를 확인하면 웜기어 접촉패턴을 확인할 수 있다.

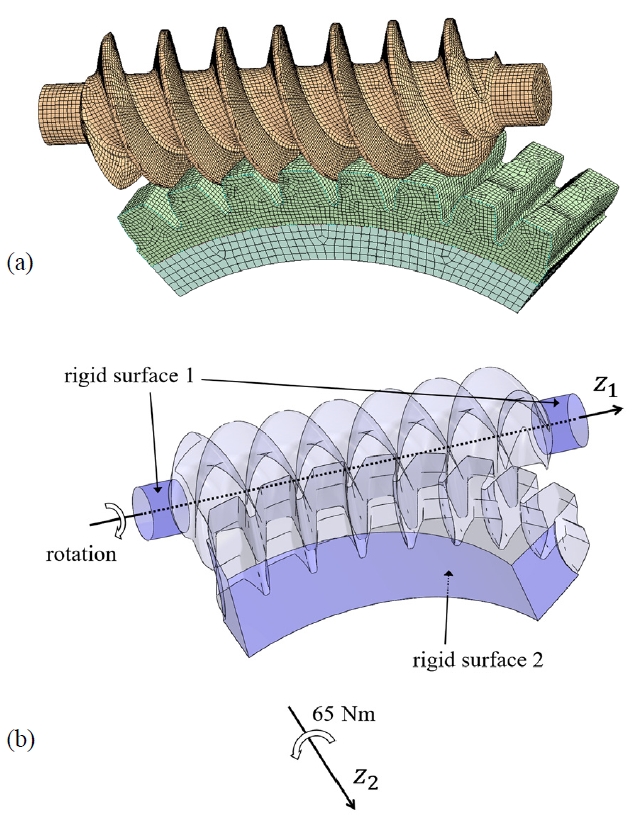
치면간격해석을 통해 계산된 접촉패턴의 교차확인을 위해 ANSYS 프로그램을 이용한 유한요소해석이 함께 수행되었다. 유한요소해석을 위한 3차원 모델은 식 (3), (6) 그리고 (8)을 이용해 산출된 웜과 웜휠 치면 좌표군을 이용하여 모델링되었다. Table 1은 예제로 사용된 웜기어의 제원을 보여준다. Fig. 5는 유한요소모델 및 경계조건을 보여준다. 요소 간 모서리 접촉으로 발생하는 해석의 불안정성을 완화시키기 위하여 웜과 웜휠의 이끝 모서리에는 반경 0.2 mm의 라운딩이 추가되었다. 유한요소해석 요소의 크기는 웜과 웜휠이 접촉하는 표면은 0.3 mm, 그 외의 부분은 0.5 mm로 설정하였으며, 웜휠 림의 안쪽 부분은 1 mm로 설정하였다. 총 요소 수는 약 21만개이다. Fig. 5(b)와 같이, 웜과 웜휠 각각과 그라운드 사이에는 각각의 회전축 위치에 회전조인트(Revolute joint)를 설정하였으며 회전조인트는 Rigid surface 로 표시된 면에 연결하였다. 웜은 설정된 각도에 따라 회전시켰으며 웜휠의 축에는 65 N･m의 모멘트를 가하였다. 웜과 웜휠 접촉면의 마찰은 무시하였으며, 비선형 접촉 계산 방법에는 Augmented Lagrange가 사용되었다. 웜은 구조용 강에 해당하는 탄성계수 200 GPa, 포아송비 0.3의 등방성 소재로 설정하였으며, 웜휠은 PA66 플라스틱에 해당하는 탄성계수 3.7 GPa, 포아송비 0.4의 등방성 소재로 설정하였다.

Table 1

Example cases of MDPS worm gear specification

Fig. 5

(a) Finite element model and (b) Boundary conditions for FEA

2.3 정렬오차 및 호브 제원에 따른 접촉패턴 변화

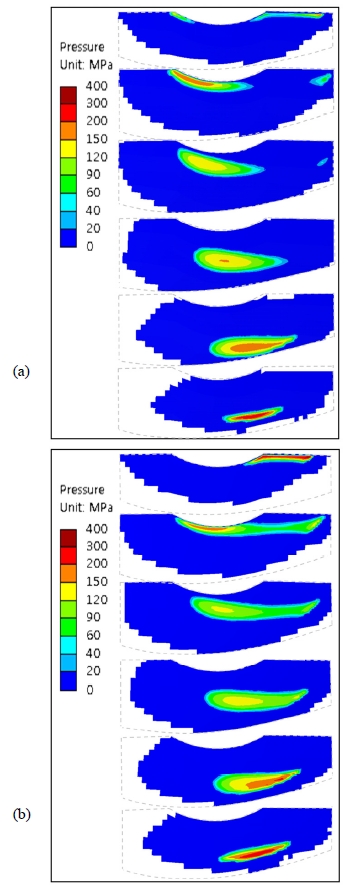
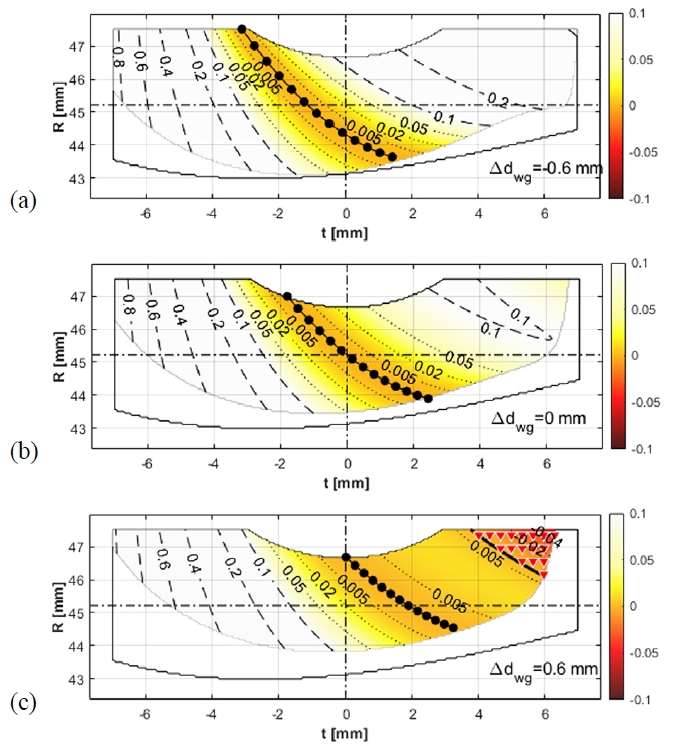
Fig. 6은 Table 1의 Case 1-a의 치면간격해석 결과를 중심거리오차 Δd_wg= -0.6 mm, 0 mm, 0.6 mm에 대하여 보여준다. 식 (9)의 ζ 값에 대한 등고선 그래프가 R과 t에 대해 나타나 있다. 검은 실선은 호브에 의해 생성된 웜휠 치면 S_g의 경계를 나타내며 그 안의 옅은 회색선은 웜 치면의 포락면 $$ S_w^E$$ 의 경계를 나타낸다. 등고선 위의 숫자는 ζ 값을 mm 단위로 나타내며 색상은 시각화를 보조하기 위해 사용되었다. 세로 1점 쇄선은 웜휠 치폭방향의 중심을, 가로 1점 쇄선은 웜휠의 피치원을 나타낸다. 웜휠 치면 가운데의 검은색 원형 점들은 ζ 값이 0이 되는 기구학적 접촉점의 궤적을 나타낸다. 실제 탄성체 접촉 시에는 ζ값이 작고 색상이 짙은 부분을 중심으로 접촉응력이 분포할 것을 예상할 수 있다. 웜과 웜휠 사이의 중심거리가 감소했을 때를 보여주는 Fig. 6(a)에서는, 표준 중심거리일 때인 Fig. 6(b)에 비해 접촉부위가 전체적으로 왼쪽으로 이동하였으나 별다른 이상 접촉은 나타나지 않았다. 그런데 중심거리가 증가한 경우인 Fig. 6(c)를 보면 웜휠 치면 윗부분 오른쪽 모퉁이에 빨간색 역삼각형 표시들이 있는데, 이는 ζ값이 0보다 작다는 표시이다. ζ값이 0보다 작다는 것은 기구학적으로 웜 치면이 웜휠 치면 안쪽으로 파고 든다는 의미이므로 간섭이 발생함을 나타낸다. Fig. 7은 Case 1-a의 유한요소해석 결과로, Δd_wg= 0 mm과 Δd_wg= 0.6 mm에 대한 접촉 위치별 접촉응력 분포를 보여준다. Fig. 6(b)를 보면 기구학적 간섭은 없으나 웜휠 치면 이끝 중앙에서 오른쪽 모퉁이로 갈수록 ζ값이 증가하다가 다시 감소하는 것을 볼 수 있는데, 이러한 특성은 Fig. 7(a)의 웜휠 이끝 부분 응력분포와 일치한다. Fig. 7(b)의 웜휠 이끝 오른쪽 모퉁이에서는 Fig. 6(c)의 결과와 같이 기구학적 간섭으로 인한 모서리 접촉이 발생하여 300 MPa이 넘는 높은 접촉응력이 나타났으며, 전반적으로 접촉응력이 웜휠 치면 오른쪽에 분포하여 치면간격해석 결과와 잘 일치하는 것을 보여준다. 웜휠 치면 아랫부분에서는 Fig. 7(a)와 Fig. 7(b)에서 공통적으로 200 MPa 이상의 접촉응력이 나타나는데, 이 부분은 웜의 이끝이 닿는 부분이며 웜에 치선수정을 적용함으로써 완화시킬 수 있으나 본 연구주제의 범위를 벗어나므로 이 논문에서는 다루지 않는다.

Fig. 6

Surface separation results of Case 1-a with misalignment (a) Δdwg= -0.6 mm, (b) Δdwg= 0 mm and (c) Δdwg= 0.6 mm

Fig. 7

Contact stress on worm wheel surface in Case 1-a with (a) Δdwg= 0 mm and (b) Δdwg= 0.6 mm

Fig. 8은 호브 줄 수가 3줄인 Table 1의 Case 1-b의 경우를, Fig. 9은 호브 줄 수가 4줄인 Table 1의 Case 1-c에 대한 치면간격해석 결과를 보여준다. Δd_wg=-0.6 mm 및 Δd_wg=0 mm에서의 결과는 호브 줄 수가 2개인 Fig. 6의 경우와 큰 차이가 없으나, Fig. 8(c)와 Fig. 9(c)를 보면 Δd_wg=0.6 mm에서는 호브의 줄 수가 증가할수록 정렬오차 발생 시 간섭현상이 줄어드는 것을 확인할 수 있다. 그러나 같은 호브 증경량일 때 호브 줄 수가 증가하면 웜휠 이빨 한 개당 절삭에 사용되는 호브 커터 날의 수가 그만큼 줄어들어서 치형의 정밀도가 떨어질 수 있으며, 호브의 리드각이 증가하기 때문에 호브 재연삭 시 어려움이 있을 수 있으므로 충분한 검토가 필요하다.

Fig. 8

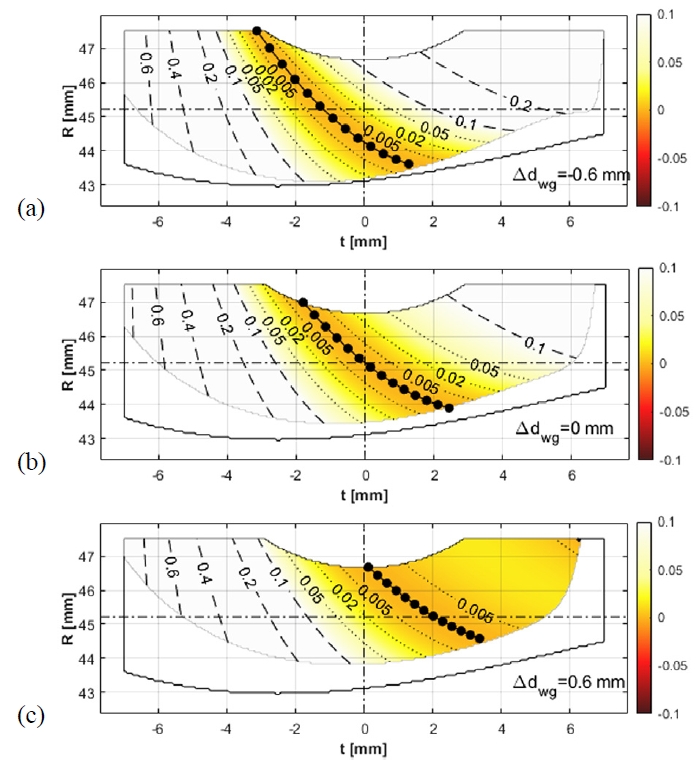
Surface separation results of Case 1-b with misalignment (a) Δdwg= -0.6 mm, (b) Δdwg= 0 mm and (c)Δdwg= 0.6 mm

Fig. 9

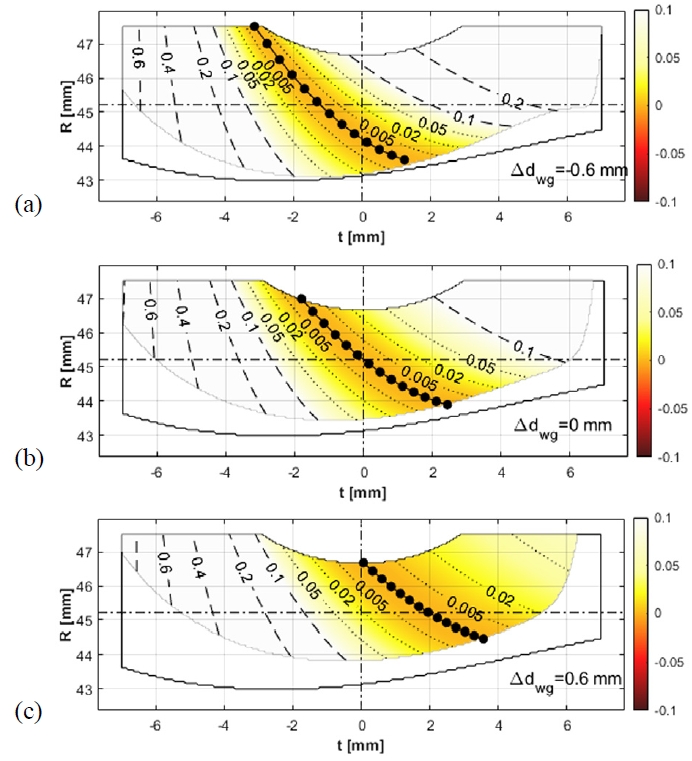
Surface separation results of Case 1-c with misalignment (a) Δdwg= -0.6 mm, (b) Δdwg= 0 mm and (c) Δdwg= 0.6 mm

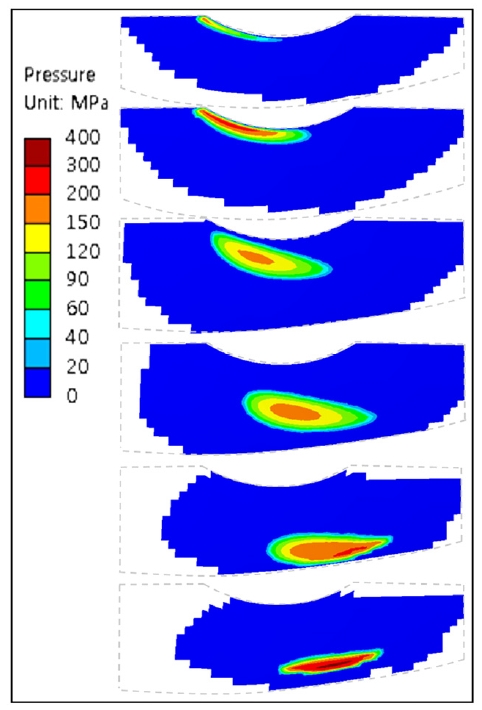
Fig. 10은 Table 1의 Case 2에 대한 치면간격해석 결과로, 호브 줄 수는 Fig. 6의 경우와 동일하게 2줄이지만 호브 증경량이 2배인 경우이다. Fig. 6과 비교했을 때, Δd_wg=-0.6 mm 및 Δd_wg=0 mm에서 큰 차이는 나타나지 않으나, 접촉점의 궤적을 중심으로 등고선 간 면적이 약간 좁아진 것을 볼 수 있다. 이는 호브 증경량이 커져서 웜휠 치면이 더 평평해졌기 때문이며, 탄성 접촉 시 접촉면적이 줄어들어서 접촉응력이 증가하게 될 것을 예상할 수 있다. Fig. 10(c)에서는 Fig. 6(c)에서 나타났던 간섭현상은 나타나지 않는 것을 확인할 수 있다. Fig. 11은 Table 1의 Case 2가 Δd_wg=0 mm일 때 접촉 위치별 접촉응력 분포를 보여준다. Fig. 11에 나타난 접촉응력이 Fig. 7(a)에 비해 평균적으로 더 높은 것을 확인할 수 있으며, Fig. 11의 웜휠 이끝 오른쪽 모퉁이에서는 모서리 접촉이 발생하지 않는 것을 볼 수 있다. 따라서 Fig. 6, Fig. 7(a), Fig. 10 그리고 Fig. 11의 결과는 호브 증경량을 증가시켜서 정렬오차 발생 시의 간섭을 피할 수는 있지만, 간섭이 발생하지 않는 부분의 접촉응력은 전체적으로 증가함을 보여준다.

Fig. 10

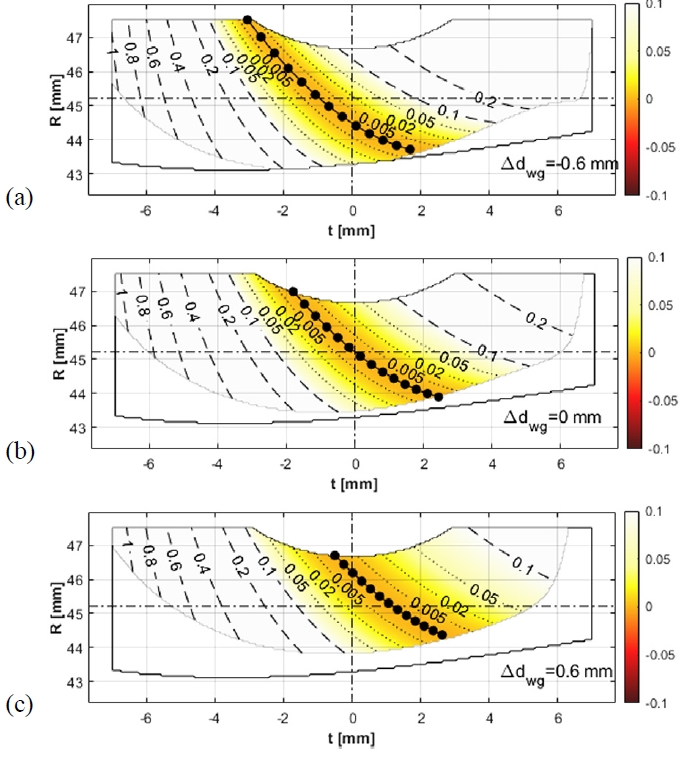
Surface separation results of Case 2 with misalignment (a) Δdwg= -0.6 mm, (b) Δdwg= 0 mm and (c) Δdwg= 0.6 mm

Fig. 11

Contact stress on worm wheel surface in Case 2 under the condition of Δdwg= 0 mm

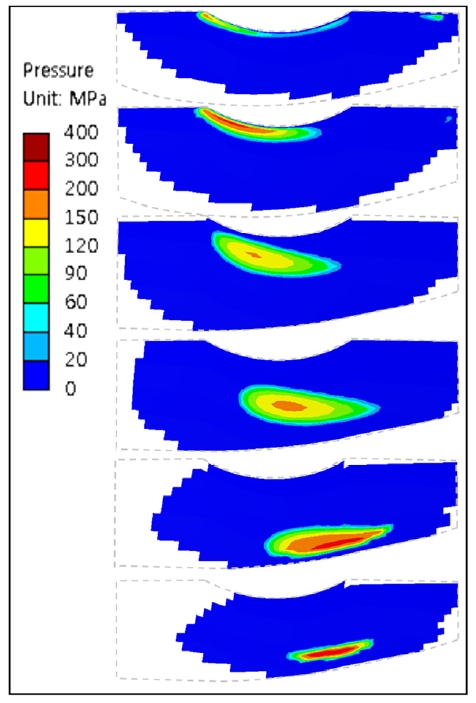
Fig. 12는 Table 1의 Case 3에 대한 치면간격해석 결과로, 호브 줄 수는 Case 1-a 에 비해 1줄을 증가시켰으며 호브 증경량은 30 %를 증가시킨 경우이다. Fig. 6와 비교했을 때, Δd_wg=-0.6 mm 및 Δd_wg=0 mm에서는 큰 차이는 없으나 Fig. 6(b)에서 나타났던 웜휠 치면 이끝 중앙에서 오른쪽 모퉁이로 갈수록 ζ값이 증가하다가 다시 감소하는 현상은 완화된 것을 볼 수 있다. Fig. 12(c)에서는 Fig. 6(c)와 달리 기구학적 간섭현상은 발견되지 않았다. Fig. 13는 Fig. 12(b)에 대한 접촉 위치별 접촉응력 분포를 보여준다. Fig. 7(a)에 비해 접촉응력이 전반적으로 약간 증가하였으나 Fig. 11보다는 낮은 접촉응력을 보여준다. 이 결과는 호브 증경량이 충분히 크지 않아서 중심거리오차 발생 시 치 간섭이 발생할 경우, 호브의 증경량만 증가시킴으로써 치 간섭을 회피할 수도 있지만, 호브 줄 수를 웜의 줄 수보다 높게 설정하면 호브의 증경량을 많이 증가시키지 않아도 치 간섭을 회피할 수 있으며, 호브의 증경량을 적게 증가시킨 만큼 접촉응력도 덜 증가시킬 수 있다는 것을 보여준다.

Fig. 12

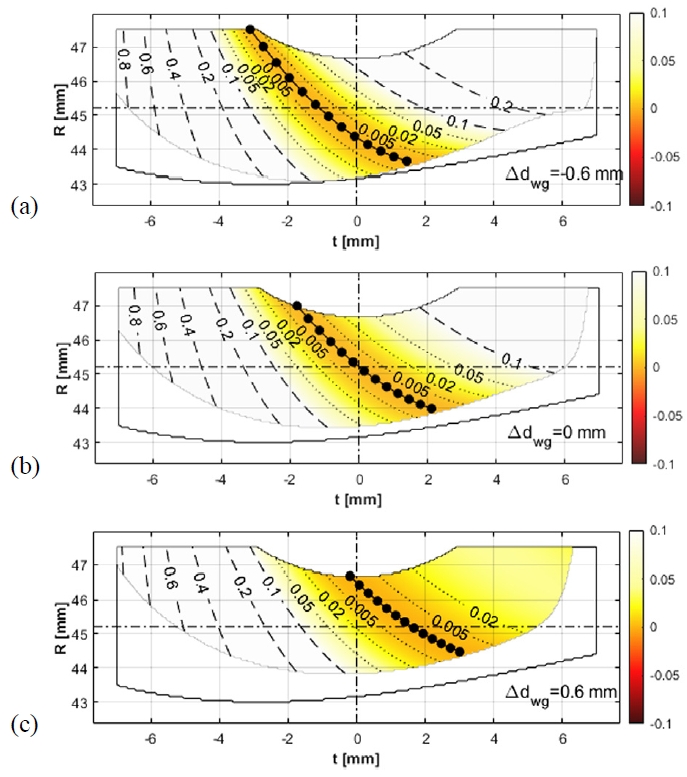
Surface separation results of Case 3 with misalignment (a) Δdwg= -0.6 mm, (b) Δdwg= 0 mm and (c) Δdwg= 0.6 mm

Fig. 13

Contact stress on worm wheel surface in Case 3 with Δdwg= 0 mm

3. 결 론

본 연구에서는 미분기하학을 이용한 치면간격해석 기법과 유한요소해석을 병행하여 MDPS 감속기용 웜기어의 접촉패턴이 호브 줄 수 및 증경량에 따라 중심거리오차 조건에서 어떻게 변화하는지를 분석하였다. 분석결과, 중심거리가 감소하는 방향으로 정렬오차가 발생할 경우에는 접촉궤적이 전체적으로 옆으로 이동하기는 하나 치 접촉에 별다른 문제가 나타나지는 않았다. 그러나 중심거리가 증가하는 방향으로 정렬오차가 발생할 경우, 웜휠 치면 상단 모퉁이에서 높은 접촉응력을 나타내는 간섭현상이 발생할 수 있음을 확인하였다. 호브의 줄 수를 증가시키거나 호브의 증경량을 증가시킬수록 간섭현상이 완화되는 것을 확인하였으며, 호브의 증경량 증가는 간섭부위가 아닌 부분에서의 접촉응력을 전체적으로 증가시키는 것을 확인하였다. 또한 호브의 줄 수와 호브의 증경량을 동시에 약간씩 증가시켰을 때에 접촉응력을 크게 증가시키지 않으면서 간섭현상을 효과적으로 회피할 수 있음을 확인하였다. 치면간격해석 결과가 보여주는 웜기어 접촉패턴은 유한요소해석 결과와 잘 일치 하였으며, MDPS 감속기용 웜기어의 접촉패턴이 호브 줄 수, 호브 증경량 그리고 중심거리오차에 따라 어떻게 변화하는지를 시각화하여 제시하였다.

Acknowledgments

본 연구는 한국기계연구원의 핵심 기계 설비 스마트설계 및 플랫폼화 기술 개발 과제의 일환으로 수행되었습니다.

References

• S. Choi and H. Kwon, “Study on the MDPS Vibration Analysis,” KSAE Spring Conference Proceedings, pp.554-559, 2009.
• S. Choi, P. Kim and K. Choi, “Study on the MDPS Vibration Analysis,” KSAE Annual Conference Proceedings, pp.2274-2283, 2009.
• F. L. Litvin and V. Kin, “Computerized Simulation of Meshing and Bearing Contact for Single-Enveloping Worm-Gear Drives,” Journal of Mechanical Design, Vol.114, No.2, pp.313-316, 1992. [https://doi.org/10.1115/1.2916948]
• A. Narayan, D. Houser and S. Vijayakar, Study of Effect of Machining Parameters on Performance of Worm Gears, AGMA 95FTM14, Alexandria, 1995.
• H. S. Fang and C. B. Tsay, “Mathematical Model and Bearing Contacts of the ZK-type Worm Gear Set Cut by Oversize Hob Cutters,” Mechanism and Machine Theory, Vol.31, Issue 3, pp.271-282, 1996. [https://doi.org/10.1016/0094-114X(95)00062-4]
• H. S. Fang and C. B. Tsay, “Mathematical Model and Bearing Contacts of the ZN-type Worm Gear Set Cut by Oversize Hob Cutters,” Mechanism and Machine Theory, Vol.35, Issue 12, pp.1689-1708, 2000. [https://doi.org/10.1016/S0094-114X(00)00024-0]
• F. L. Litvin, I. Gonzalez-Perez, K. Yukishima, A. Fuentes and K. Hayasaka, “Design, Simulation of Meshing, and Contact Stresses for an Improved Worm Gear Drive,” Mechanism and Machine Theory, Vol.42, Issue 8, pp.940-959, 2007. [https://doi.org/10.1016/j.mechmachtheory.2006.08.005]
• V. Simon, “Load Distribution in Cylindrical Worm Gears,” Journal of Mechanical Design, Vol.125, No.2, pp.356-364, 2003. [https://doi.org/10.1115/1.1561043]
• V. Simon, “Computer Aided Loaded Tooth Contact Analysis in Cylindrical Worm Gears,” Journal of Mechanical Design, Vol.127, No.5, pp.973-981, 2005. [https://doi.org/10.1115/1.1904050]
• V. Simon, “The Influence of Gear Hobbing on Worm Gear Characteristics,” Journal of Manufacturing Science and Engineering, Vol.129, No.5, pp.919-925, 2007. [https://doi.org/10.1115/1.2752524]
• J. Sohn and N. Park, “Geometric Interference in Cylindrical Worm Gear Drives Using Oversized Hob to Cut Worm Gears,” Mechanism and Machine Theory, Vol.100, pp.83-103, 2016. [https://doi.org/10.1016/j.mechmachtheory.2016.02.002]
• J. Sohn and N. Park, “Study on the Influence of Gear Hobbing and Shaft Misalignments on the Geometric Interference of Cylindrical Worm Gear Set,” Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol.231, No.24, pp.4646-4654, 2017. [https://doi.org/10.1177/0954406216671543]
• J. Sohn and N. Park, “Modified Worm Gear Hobbing for Symmetric Longitudinal Crowning in High Lead Cylindrical Worm Gear Drives,” Mechanism and Machine Theory, Vol.117, pp.133-147, 2017. [https://doi.org/10.1016/j.mechmachtheory.2017.07.004]
• F. L. Litvin, I. Gonzalez-Perez, A. Fuentes and D. Vecchiato, “Generalized Concept of Meshing and Contact of Involute Crossed Helical Gears and Its Application,” Computer Methods in Applied Mechanics and Engineering, Vol.194, Issues 34-35, pp.3710-3745, 2005. [https://doi.org/10.1016/j.cma.2004.09.009]
• F. L. Litvin and A. Fuentes, Gear Geometry and Applied Theory, 2nd Edn., Cambridge University Press, New York, 2004. [https://doi.org/10.1017/CBO9780511547126]