무향 칼만 필터를 이용한 타이어 수직하중 변화 추정

1. 서 론

최근 지능형 자동차에 관한 연구가 활발히 진행되면서, 정확한 자세 제어를 위한 능동안전시스템(Active Safety System)의 중요성이 커지고 있다. 능동안전과 관련된 대표적인 섀시 제어로는 Electronic Stability Control(ESC), Torque Vectoring System(TVS), Continuous Damping Control(CDC), Active Front Steering(AFS)과 같은 것들이 있다.¹⁾ 이들은 차량의 선회안정성을 향상시키기 위해 개발되었기 때문에, 차량 모션과 관련된 정보가 필요하다.

자동차는 선회운동시 원심력에 의해 수직하중의 이동이 발생하게 되는데, 이는 차량의 선회 안정성 및 조정성에 중요한 영향을 미친다. 타이어 수직력은 차량의 내부센서(In-Vehicle-Sensor)에서 직접 측정이 되지 않기 때문에, 이를 계산 하기 위한 여러 방법들이 제안되었다.^2-4) 먼저 전 차량 모델을(Full Car Model) 이용하는 방법이 논의되었지만, 해당 모델은 서스펜션 역학(Suspension Dyna-mics) 및 타이어의 비선형적인 특성 때문에 효과적인 제어전략의 수립이 어려웠다.⁵⁾ 이러한 이유들 때문에, 간략화된 모델을 사용하여 타이어 수직력을 추정하는 방법들이 연구되었다. 윤장열 등⁶⁾과 조완기 등⁷⁾은 차량의 Inertial Measurement Unit(IMU) 센서와 3-DOF Vehicle Model을 바탕으로 한 Steady-State Kalman Filter(KF)를 설계하였다. 하지만 이러한 추정방법은 차량의 실시간 정보를 업데이트 하지 못하기 때문에, 다양한 주행 환경 변화를 정확히 반영하지 못한다. 윤성환 등⁸⁾은 Plane Roll Model의 파라미터를 변경하였으나, 실제 다양한 도로 환경에서의 차량 파라미터는 알기 어렵기 때문에 해당 방식은 그 정확성이 떨어진다.

본 연구에서는 타이어 수직력 추정기의 성능을 개선하기 위해 보다 향상된 추정 알고리즘을 제안한다. 먼저 차량의 IMU센서에서 측정되는 횡가속도 및 요레이트 정보로만으로는 미끄러운 도로 환경에서 발생되는 선회 특성을 정확히 반영하지 못하기 때문에, 롤 레이트를 측정값으로 추가하였다. 롤 레이트는 차량의 수직방향 고유 주파수 특성으로 구성되어 있으므로, 다양한 도로 노면 환경에서의 차량 응답 특성을 얻을 수 있다.⁹⁾ KF의 경우는 Ricatti equation에서 계산된 고정된 게인값을 사용하기 때문에, 주행중인 차량 정보를 실시간으로 반영하지 못한다. 본 연구에서는 선형 모델을 사용하였기 때문에 Extended Kalman Filter(EKF)를 사용하지 않았다.⁶⁾ 그러므로 Unscented Kalman Filter(UKF)에 기반한 추정기 알고리즘을 사용하여, 게인을 지속적으로 업데이트 한다. 이를 통해 미끄러운 주행 환경에서의 차량 정보를 실시간으로 반영할 수 있다.

제안된 방법의 검증을 위해 차량 동역학 Simulation 프로그램인 CarSim을 사용하였다. Dry Asphalt에서는 이전에 방법과 제시된 방법간의 성능차이가 유의미하지 않았다. 하지만 Ice Road 상에서는 Tire slip angle이 2도 이상 발생되면서 Lateral Force가 Saturation 영역을 넘어가게 된다. 이로 인해 비선형성이 증가하여 두 가지 방법의 성능차이가 크게 발생했다. 따라서 제안된 방법은 낮은 도로 마찰 계수 상황에서 유효한 방법임이 검증되었다.

본 논문은 총 5개의 장으로 이루어져 있으며, 그 구성은 다음과 같다. 2장, 3장에서는 차량의 타이어 수직력을 모델링하며 추정기 알고리즘을 설명한다. 4장에서는 제안된 추정기를 설계하여, 차량 동역학 해석프로그램인 CarSim으로 그 성능을 검증하였다.

2. 차량의 수직역학 모델링

본 장에서는 차량의 수직역학을 모델링하여 타이어 수직력을 추정한다. 먼저 2.1절에서는 타이어 수직력 추정기 구조도를 제시하며, 2.2절에서는 차량의 수직역학을 모델링하는 과정에 대해 설명한다.

2.1 타이어 수직력 추정기 구조도

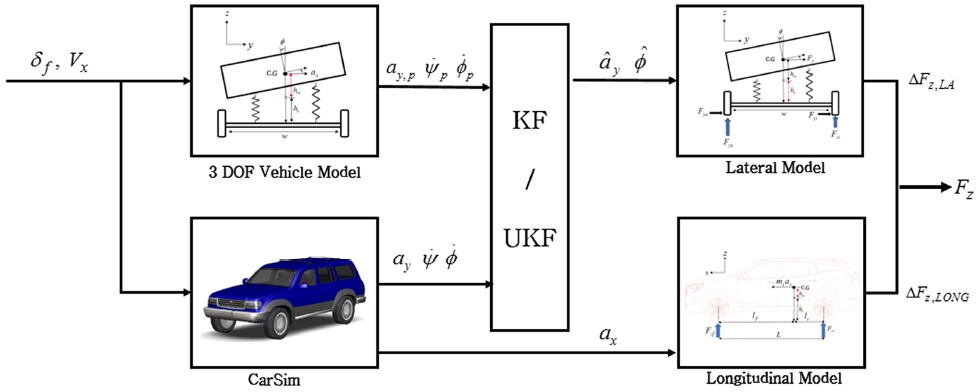
본 연구에서 제시한 타이어 수직력 추정기 구조도는 Fig. 1과 같다. 해당 구조도에서는 입력으로 종방향 속도와 조향각이 주어졌을 때, 횡 가속도 와 요 레이트, 롤 레이트가 계산 및 측정되는 과정을 보여준다.⁶⁾ 이후 해당 데이터들을 입력으로 하는 추정기(KF/UKF)를 통해 횡 가속도와 롤 각을 추정한다. 이렇게 추정된 값들을 이용하여 횡방향 하중이동을 구하고, 차량의 종 가속도로부터 종방향 하중이동을 구한다. 이를 바탕으로 각 바퀴의 타이어 수직력을 추정한다.

Fig. 1

Structure of vertical tire forces estimation

2.2 수직역학 모델링

이번절에서는 타이어 수직력 추정에 사용될 Bicycle Model, Simple Roll Model, Lateral/Longitudinal Load Transfer Model에 대해 설명한다.

2.2.1 Bicycle Model

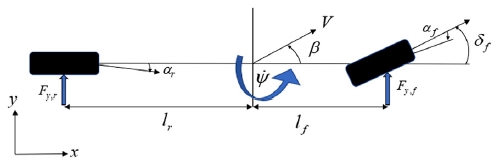
차량의 횡방향 움직임에 대한 동역학을 묘사하기 위해, 차량이 고속으로 주행하는 상황을 가정한다. 이로 인해 선회반경은 차량의 축거 보다 훨씬 크고, 조향각의 범위가 작은 범위에 존재하면, 전후륜의 내측과 외측을 아래 Fig. 2와 같이 하나의 휠로 나타낼 수 있다.^2,10)

Fig. 2

Bicycle model

또한 도로의 경사각이 없을 때 y 축에 대하여 뉴턴의 제2 법칙을 적용하면, 다음 식 (1)과 같이 표현된다.

$\[ {ma}_y=F_{yf}+F_{yr} \]$

(1)

선회하는 차량의 횡 가속도는 y 축에 의한 모션과 구심가속도에 의한 성분을 더하여, 식 (2)와 같이 나타낼 수 있다.

$\[ a_y=\ddot{y}+V_x\dot{\Psi } \]$

(2)

이를 이용하여 차량의 횡방향 병진운동을 정리하면, 식 (3)과 같다.

$\[ m\left(\ddot{y}+V_x\dot{\Psi }\right)=F_{yf}+F_{yr} \]$

(3)

또한 z 축에 대한 모멘트 평형식을 구하면 식 (4)와 같이 표현할 수 있다.

$\[ I_z\dot{\Psi }=l_f{F}_{yf}-l_r{F}_{yr} \]$

(4)

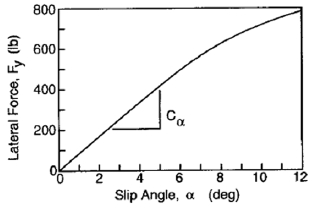
자동차가 고속으로 주행 중인 상황에서는, 차량의 진행 방향과 타이어의 진행방향이 일치하지 않게 된다. 이로 인해 타이어에는 슬립이 발생된다. 이때 슬립각이 작은 범위에 있다면 Fig. 3과 같이 횡력과 선형적인 관계를 갖고 있으며, 이는 식 (5)와 같이 표현될 수 있다.^11,12)

Fig. 3

Relation between slip angle and lateral force

$\[ F_y=C_{\alpha } \alpha \]$

(5)

작은 각 범위에서는 전후륜의 슬립각을 아래 식 (6)과 식 (7)로 근사화할 수 있다.

$\[ {\alpha }_f=\frac{\dot{y}+l_f\dot{\Psi }}{V_x} \]$

(6)

$\[ {\alpha }_r=\frac{\dot{y}-l_r\dot{\Psi }}{V_x} \]$

(7)

이상에서 식 (3)~(7)을 정리하면 아래 식 (8)과 같은 상태 공간 방정식의 형태로 나타낼 수 있다.

상태변수 $$ x=\left[\begin{array}{cc}\dot{y}\hfill & \dot{\Psi }\hfill \end{array}\right]$$ 에 대하여 입력 u=δ_f 라 하면,

$$ \dot{x}=Ax+Bu$$

여기서

$\[ \begin{array}{c}\begin{array}{cc}A=\left[\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right]\hfill & B=\left[\begin{array}{c}{b}_{11}\\ b_{21}\hfill \end{array}\right]\end{array}\hfill \\ a_{11}=-\frac{2\left(C_{\alpha f}+C_{\alpha }r\right)}{m{V}_x},a_{12}=\frac{2\left(l_r{C}_{\alpha r}-l_f{C}_{\alpha f}\right)}{m{V}_x}-V_x,\hfill \\ a_{21}=-\frac{2\left(C_{\alpha f}{l}_f-C_{\alpha r}{l}_r\right)}{I_z{V}_x},a_{22}=\frac{-2\left({l^2}_r{C}_{\alpha r}+{l^2}_f{C}_{\alpha f}\right)}{I_z{V}_x}\hfill \\ b_{11}=\frac{2C_{\alpha f}}{m},b_{21}=\frac{2l_f{C}_{\alpha f}}{I_z}\text{이다.}\hfill \end{array} \]$

(8)

2.2.2 Simple Roll Model

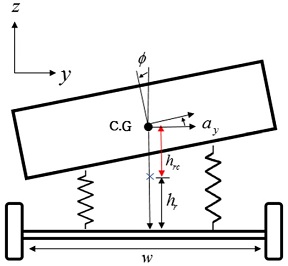
앞의 Fig. 2에서 제시된 Bicycle Model은 롤이 발생하지 않는, 평면 움직임의 영역만을 다루었다. 그러나 실제 차량은 선회시 횡 가속도에 의해 아래 Fig. 4와 같이 롤 이 발생된다.^6,13,14)

Fig. 4

Simple roll model

이때 차량은 요철이 없는 평지를 주행한다고 가정하면, 서스펜션의 역학을 2개의 스프링과 댐퍼로 단순화 할 수 있다. 이때 횡 가속도에 의해 발생된 롤 모멘트를 고려하여, 롤 축에 대한 토크평형식을 구하면 아래 식 (9)와 같이 표현할 수 있다. 이때 롤 각이 작다고 가정하면 (sinϕ≃ϕ, cosϕ≃1) 식 (10)과 같이 정리될 수 있다.¹⁵⁾

$\[ I_x\ddot{\varphi }=-m_s{a}_y{h}_{rc}\cos \varphi +m_{s}g{h}_{rc}\sin \varphi -K_{roll}\varphi -C_{roll}\dot{\varphi } \]$

(9)

$\[ \ddot{\varphi }=-\frac{m_s{a}_y{h}_{rc}}{I_x}+\frac{\left(m_{s}g{h}_{rc}-K_{roll}\right)\varphi }{I_x}-\frac{C_{roll}\dot{\varphi }}{I_x} \]$

(10)

2.2.3 Lateral Load Transfer Model

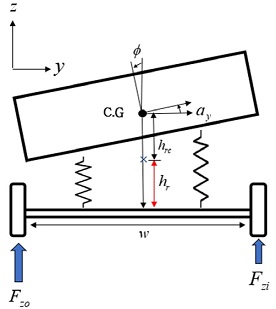
아래 Fig. 5에서는 좌/우 수직력과 횡 방향힘, 롤 영향을 고려하여 뉴턴의 제2법칙을 적용한다. 이를 통해 좌/우 수직하중의 변화를 아래 식 (11)로 표현할 수 있다.^11,16,17)

Fig. 5

Latereal load transfer model

$\[ F_{zi}\frac{w}{2}-F_{zo}\frac{w}{2}-F_y{h}_r=I_x\ddot{\varphi }+C_{roll}\dot{\varphi }+K_{roll}\varphi \]$

(11)

$\[ \mathrm{\Delta }{F}_{z,LA}=\left(F_{zi}-F_{zo}\right)=\frac{\left(2F_y{h}_r+2K_{roll}\varphi \right)}{w} \]$

(12)

이때 차량이 정상상태에서 선회한다고 가정하면, 식 (12)로 정리할 수 있다($$ \ddot{\varphi }=\dot{\varphi }=\varphi $$). 즉 차량에서 발생되는 수직하중의 변화는 선회력에 의한 횡방향 하중 이동과 롤 역학에 의한 하중이동의 합으로 정의할 수 있다.

2.2.4 Longitudinal Load Transfer Model

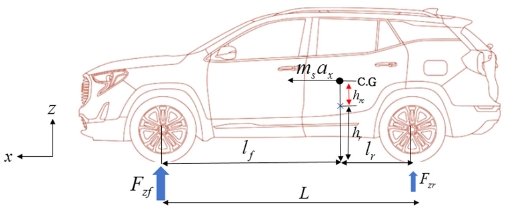
차량이 일정한 속도로 주행하면서 선회를 하면, Fig. 6과 같이 종방향 가속도에 변화가 발생한다.^7,18,19)

Fig. 6

Longitudinal load transfer model19)

이는 전후륜 수직하중의 변화를 일으키기 때문에, 타이어 수직력 추정시 고려될 필요가 있다. 차량의 무게중심과 롤센터 사이에서 발생되는 종방향 힘과 전후륜 수직력 사이의 토크 평형식을 고려하면, 식 (13)과 같이 표현할 수 있다.

$\[ F_{zr}L-F_{zf}L+F_x{h}_{rc}=I_x\ddot{\varphi }+C_{roll}\dot{\varphi }+K_{roll}\varphi \]$

(13)

$\[ \mathrm{\Delta }{F}_{z,LONG}=\left(F_{zr}-F_{zf}\right)=-\frac{F_x{h}_{rc}}{L}=-\frac{m{a}_x{h}_{rc}}{L} \]$

(14)

이때 차량이 정상상태에서 주행하고 있다고 가정하면($$ \ddot{\varphi }=\dot{\varphi }=\varphi $$), 이를 식 (14)와 같이 정리할 수 있다.⁴⁾

2.2.5 각 바퀴의 수직력 계산

자동차의 타이어 수직력을 계산하기 위해서는 정적인 상태에서의 하중을 기준으로 종/횡방향 수직하중 변화를 고려해야 한다. 여기서 정적인 상태의 하중은 차량을 저속으로 주행시킨 상황에서 계측한 값을 기준으로 삼았다. 앞의 2.2.3절과 2.2.4절에서 구한 횡방향 하중이동, 종방향 하중이동의 변화를 고려한 각 바퀴의 수직력은 Fig. 7과 같고, 다음 식 (15)와 같이 정리할 수 있다.^7,20)

Fig. 7

Calculation of vertical tire force of each wheel20)

$\[ \begin{array}{c}{F}_{z,fL}=\frac{1}{2}{F}_f+\text{Δ}{F}_{zf,LA}-\text{Δ}{F}_{z,LONG}\hfill \\ F_{z,fR}=\frac{1}{2}{F}_f-\text{Δ}{F}_{zf,LA}-\text{Δ}{F}_{z,LONG}\hfill \\ F_{z,rL}=\frac{1}{2}{F}_r+\text{Δ}{F}_{zr,LA}+\text{Δ}{F}_{z,LONG}\hfill \\ F_{z,rR}=\frac{1}{2}{F}_r-\text{Δ}{F}_{zr,LA}+\text{Δ}{F}_{z,LONG}\hfill \end{array} \]$

(15)

3. 타이어 수직력 추정기 설계

3장에서는 앞의 2장에서 사용된 모델들을 바탕으로 3-DOF 차량동역학을 모델링하고, 4장에서 설계될 2가지의 추정기 알고리즘을 설명한다.

4. 시뮬레이션 및 결과

4.1 시뮬레이션 조건

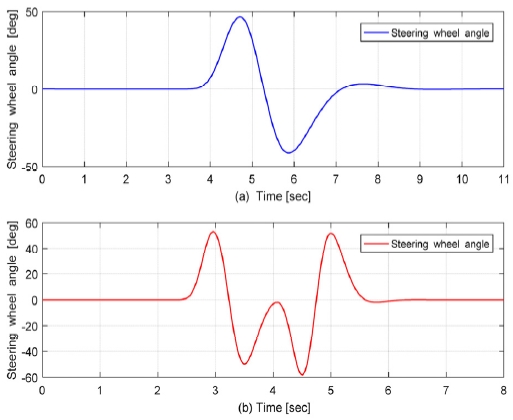
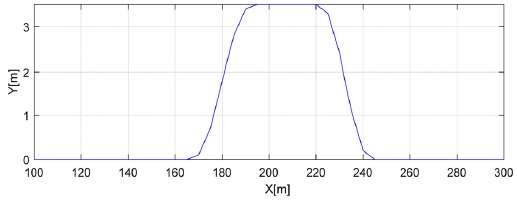
본 연구에서 제시한 타이어 수직력 추정기 알고리즘을 검증하기 위해 MATLAB/CarSim을 이용하였다. 그리고 다음과 같은 주행 시나리오를 상정하였다. 시나리오는 Single Lane Change 상황(시속 70 km/h)과 Double Lane Change(시속 50 km/h) 상황으로 분류하였다. 그리고 이를 다양한 노면 마찰계수 상황에서 시뮬레이션을 진행하였다. 이때 True 값은 CarSim에서 계측된 값을 의미한다.

Table 1

E-Class SUV Parameter

4.1.1 시뮬레이션 조건 및 도로 환경

(1) Steering wheel angle

Fig. 8

Steering wheel angle (a) Single lane change, (b) Double lane change

(2) Vehicle trajectory

Fig. 9

Vehicle trajectory

4.2 시뮬레이션 결과

4.2.1 Single lane change (Mu=1.0)

4.2.2 Single Lane Change (Mu=0.2)

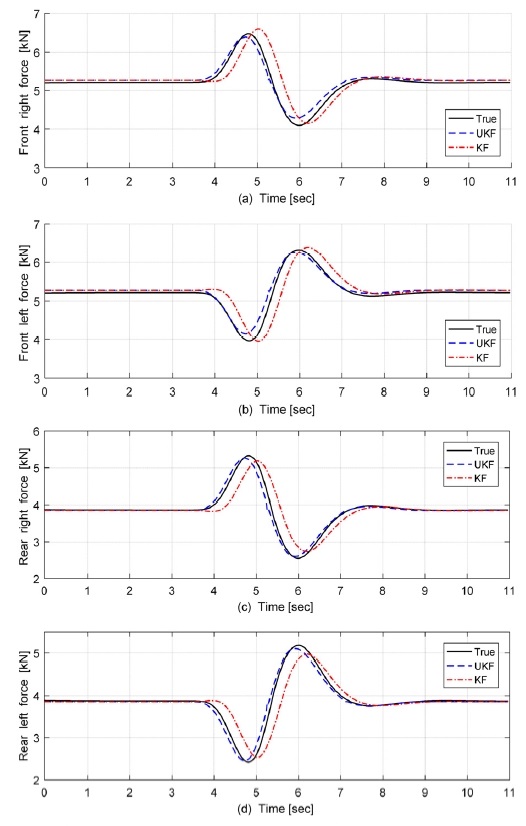
제시된 Single Lane Change에서 Fig. 10과 같이 도로 노면 마찰계수가 1.0인 상황에서는 Steady-State-KF 와 UKF의 성능은 유사하였다. 그러나 Fig. 11에서와 같이 도로 노면마찰계수가 0.2인 상황에서는 UKF의 추정값이 Ground Truth와 더 일치하는 경향을 보였다.

Fig. 10

Vertical tire forces estimation (a) Front right, (b) Front left, (c) Rear right, (d) Rear left [kN]

Fig. 11

Vertical tire forces estimation (a) Front right, (b) Front left, (c) Rear right, (d) Rear left [kN]

4.2.3 Double Lane Change(Mu=1.0)

4.2.4 Double Lane Change (Mu=0.2)

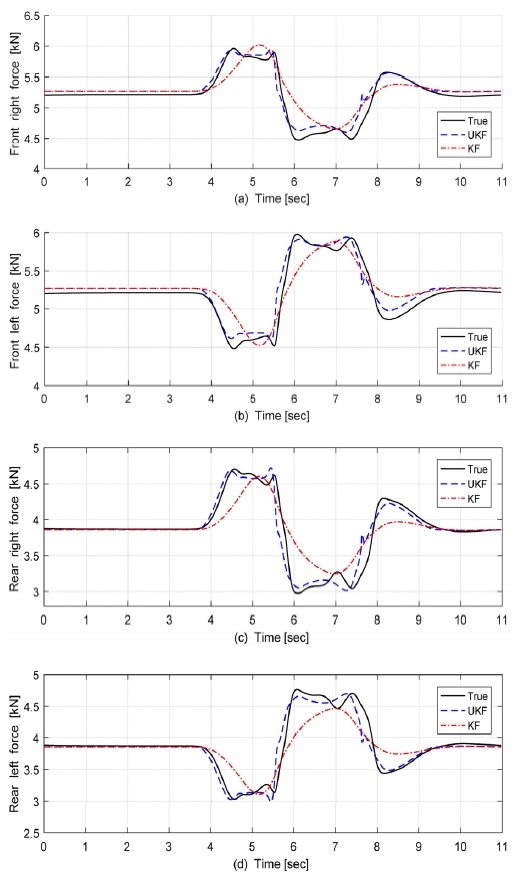
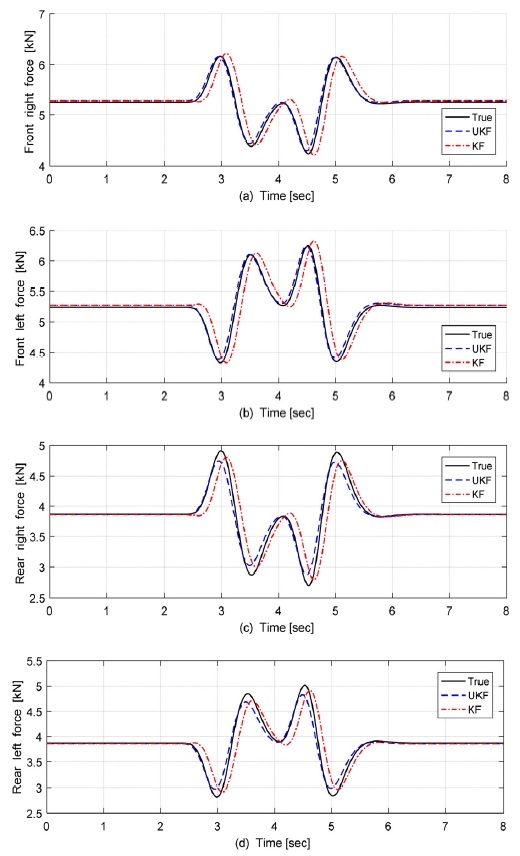
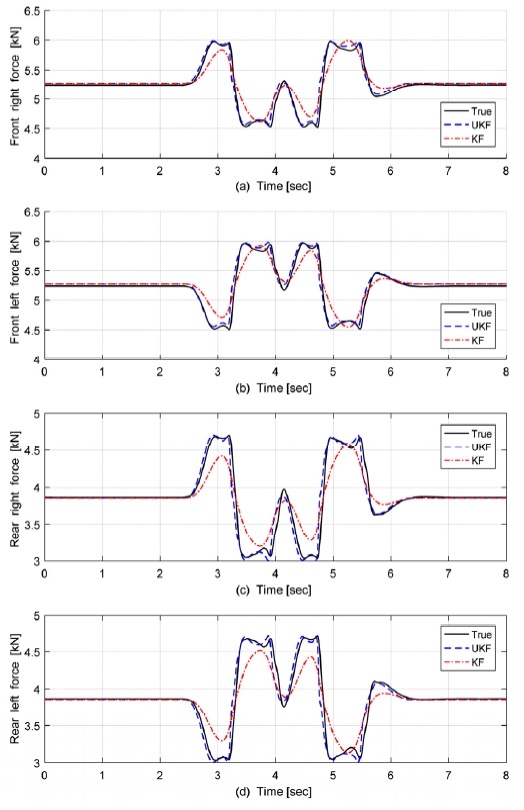
제시된 Dobule Lane Change에서 Fig. 12에서와 같이 도로 노면 마찰계수가 1.0인 상황에서는 Steady-State-KF와 UKF의 성능은 유사하였다. 그러나 Fig. 13에서와 같이 도로 노면마찰계수가 0.2인 상황에서는 UKF의 추정값이 Ground Truth와 더 일치하는 경향을 보였다. 즉 Ice Road 상에서는 Tire slip angle이 2도 이상 발생하면서, Lateral Force가 Saturation 영역을 넘어가게 된다. 이로 인해 비선형성이 증가하여 두 가지 방법의 성능차이가 크게 발생했다.

Fig. 12

Vertical tire forces estimation (a) Front right, (b) Front left, (c) Rear right, (d) Rear left [kN]

Fig. 13

Vertical tire forces estimation (a) Front right, (b) Front left, (c) Rear right, (d) Rear left [kN]

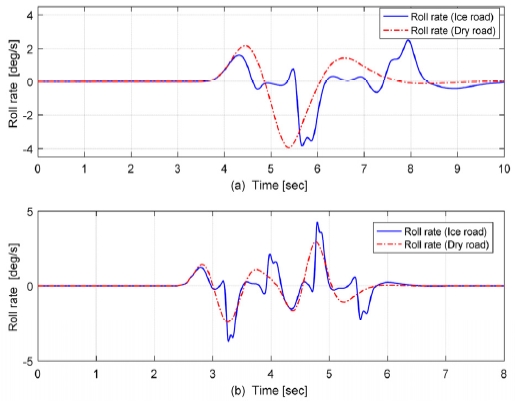
4.3 차량의 Roll rate 비교

Fig. 14는 CarSim에서 계측된 롤 레이트를 비교하였다. 마찰계수가 1인 상황에서는 롤 레이트가 사인파 형태로 움직인 반면, 마찰계수가 0.2인 경우에는 불규칙적으로 움직였다. 후자의 경우와 같이 비정상적인 선회상황에서는 타이어가 그립을 잃게 된다. 따라서 UKF에 기반한 추정기를 통해 롤 레이트의 변화된 특성을 반영하여, 타이어 수직력을 추정해야 한다.

Fig. 14

Measured roll rate (a) Single Lane Change (b) Double Lane Change

4.4 RMSE (Root Mean Square Error) 비교

아래 Table 2 ~ Table 5를 통해 제안된 Lane Change/ Double Lane Change 상황에서 UKF가 추정한 타이어 수직력이 KF가 추정한값보다 Ground Truth와 의 RMSE가 적은 것으로 나타났다.

Table 2

RMSE of vertical tire forces : Lane change (Mu=1.0)

Table 3

RMSE of vertical tire forces : Lane change (Mu=0.2)

Table 4

RMSE of vertical tire forces : Double lane change (Mu=1.0)

Table 5

RMSE of Vertical tire forces : Double lane change(Mu=0.2)

5. 결 론

본 연구에서는 UKF를 이용한 타이어 수직력 추정기 알고리즘을 제시하였다. 제안한 타이어 수직력 추정기를 검증하기위해 Single Lane Change, Double Lane Change 주행상황을 상정하였고, 각각 아스팔트 도로와 빙판길 도로 조건으로 분류하여 시뮬레이션을 진행하였다. 시뮬레이션 결과 도로 마찰계수가 낮은 상황에서는 비정상적인 선회상황이 발생하여 Covariance를 지속적으로 업데이트해야할 필요성이 있었다. 또한 제시된 추정알고리즘은 Mu값이 0.2~1.0 사이에서 유효한 결과를 보인 것으로 관찰되었다. 즉 미끄러운 도로에서 타이어 수직력 추정시 Covariance를 업데이트 하는 UKF 알고리즘을 적용하여 추정성능을 높일 필요가 있다. 이를 통해 정확한 타이어 수직력 정보가 필요한 여러 샤시 제어시스템에 적용한다면 그 성능이 향상될 것으로 기대된다.

Acknowledgments

A part of this paper was presented at the KSAE 2018 Fall Conference and Exhibition

본 연구는 2019 년도 산업통상자원부 및 산업기술평가관리원(KEIT) 연구비 지원(20000293, 환경센서와 차량내부센서 융합기반 노면상태 검출 기술 개발) 과 산업통상자원부 및 중소벤처기업부의 연구비 지원(S2367759, 통합 이종카메라 시스템을 이용한 운전자지원시스템 개발) 에 의하여 연구되었음.

References

• W. Cho, J. Choi, C. Kim, S. Choi and K. Yi, “Unified Chassis Control for the Improvement of Agility, Maneuverability, and Lateral Stability,” IEEE Transactions on Vehicular Technology, Vol.61, No.3, pp.1008-1020, 2012. [https://doi.org/10.1109/TVT.2012.2183152]
• H. B. Pacejka, Tyre and Vehicle Dynamics, Butterworth-Heinemann, Oxford, 2002.
• S. Song, M. C. K. Chun, J. Huissoon and S. L. Waslander, “Pneumatic Trail Based Slip Angle Observer with Dugoff Tire Model,” IEEE Intelligent Vehicles Symposium Proceedings, pp.1127-1132, 2014. [https://doi.org/10.1109/IVS.2014.6856538]
• A. Rezaeian, R. Zarringhalam, S. Fallah, W. Melek, A. Khajepour, S. -Ken Chen, N. Moshchuck and B. Litkouhi, “Novel Tire Force Estimation Strategy for Real-time Implementation on Vehicle Applications,” IEEE Transactions on Vehicular Technology, Vol.64, No.6, pp.2231-2241, 2015. [https://doi.org/10.1109/TVT.2014.2345695]
• J. Daknlallah, S. Glaser, S. Mammar and Y. Sebsadji, “Tire-road Forces Estimation Using Extended Kalman Filter and Sideslip Angle Evaluation,” American Control Conference, pp.4597-4602, 2008. [https://doi.org/10.1109/ACC.2008.4587220]
• J. Yoon, D. Kim and K. Yi, “Design of a Rollover Index based Vehicle Stability Control Scheme,” Vehicle System Dynamics, Vol.45, No.5, pp.459-475, 2007. [https://doi.org/10.1080/00423110701245165]
• W. Cho, J. Yoon, S. Yim, B. Koo and K. Yi, “Estimation of Tire Forces for Application to Vehicle Stability Control,” IEEE Transactions on Vehicular Technology, Vol.59, No.2, pp.638-649, 2010. [https://doi.org/10.1109/TVT.2009.2034268]
• S. H. Yun, J. G. Yang, C. S. Kim and K. S. Huh, “A Study of Vertical Load Estimation for 4-wheel Torque Vectoring Control,” KSAE Fall Confenrence Proceedings, pp.211-213, 2016.
• S. W. Kim, Y. W. Jeong, J. S. Kim, S. -H. Lee and C. C. Chung, “Vehicular Vertical Tire Foces Estimation Using Unscented Kalman Filter,” Asian Control Conference, pp.325-330, 2019.
• R. Rajamani, Vehicle Dynamics and Control, Springer, New York, 2012. [https://doi.org/10.1007/978-1-4614-1433-9]
• T. D. Gillespie, Fundamentals of Vehicle Dynamics, Society of Automotive Engineers, Warrendale, 1992. [https://doi.org/10.4271/R-114]
• R. N. Jazar, Vehicle Dynamics: Theory and Applications, Springer, New York, 2008. [https://doi.org/10.1007/978-0-387-74244-1]
• A. Hac, T. Brown and J. Martens, “Detection of Vehicle Rollover,” SAE 2004-01-1757, 2004. [https://doi.org/10.4271/2004-01-1757]
• M. Doumiati, A. Charara, A. Victorino and D. Lechner, Vehicle Dynamics Estimation Using Kalman Filtering: Experimental Validation, Wiley, Hoboken, 2013. [https://doi.org/10.1002/9781118578988]
• S. Bae, J. R. Yun, J. M. Lee and T. O. Tak, “An Effect of the Complexity in Vehicle Dynamics Models on the Analysis of Vehicle Dynamics Behaviors: Model Comparison and Validation,” Transactions of KSAE, Vol.8, No.6, pp.267-278, 2000.
• D. C. Barton and J. D. Fieldhouse, Automotive Chassis Engineering, Springer, New York, 2018.
• J. Reimpell, H. Stoll and J. W. Betzler, The Automotive Chassis: Engineering Principles, SAE International, Woburn, 2001.
• M. Meywerk, Vehicle Dynamics, Wiley, West Sussex, 2015.
• GMC Terrain SLE/SLT, https://www.gmc.com/suvs/terrain-smallsuv, , 2019.
• Auto-Tech-Review, Technology, https://autotechreview.com/technology/tech-update/sensors-ecus-actuators-to-boost-suspension-performance, , 2019.
• J. L. Crassidis and J. L. Junkins, Optimal Estimation of Dynamic Systems, Chapman and Hall, Florida, 2004. [https://doi.org/10.1201/9780203509128]
• V. Kordic, Kalman Filter, InTech, Vukovar, 2010. [https://doi.org/10.5772/233]
• S. W. Kim, Vertical Tire Forces Estimation and Active Steering Control Considering Roll Dynamics of Vehicle, M. S. Thesis, Hanyang University, Seoul, 2019.
• S. W. Kim, Y. W. Jeong, J. S. Kim, S. -H. Lee and C. C. Chung, “Design of Roll Angle Estimator for Vehicles Using Unscented Kalman Filter,” KSAE Fall Conference Proceedings, pp.495-500, 2018.