Deep Q - Networks 기반의 하이브리드차량의 에너지관리전략 개발
Copyright Ⓒ 2019 KSAE / 168-10
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
The fuel economy of a hybrid electric vehicle(HEV) is vastly influenced by the manner power is distributed. A dynamic, programming-based power distribution strategy can provide a global optimal solution, but it is not applicable to an actual vehicle because it requires further driving information. On the other hand, the reinforcement learning-based power distribution strategy is highly applicable to an actual vehicle because it requires only the current state to construct the policy. Recently, deep Q-networks(DQN) have been developed by applying a deep neural network to reinforcement learning, leading to significant change in the field of reinforcement learning. DQN could solve complex tasks efficiently based on different studies. In this particular study, we developed an energy management strategy for HEVs that is applicable to actual vehicles, and can achieve high efficiency through the DQN.
Keywords:
Hybrid electric vehicle, Energy management, Parallel hybrid electric vehicle, Deep neural network, Reinforcement learning키워드:
하이브리드 차량, 에너지관리, 병렬형 하이브리드 차량, 심층 인공신경망, 강화학습1. 서 론
지구온난화와 심화되는 대기오염으로 인해서 차량 연비와 배기가스에 대한 전 세계적인 규제가 강화되면서 친환경 차량에 대한 지속적인 연구와 개발이 계속 이루어지고 있다.1) 하이브리드 차량은 대표적인 친환경 차량으로 두 개 이상의 동력원을 사용하는 차량을 의미한다.
하이브리드 차량은 두 개 이상의 동력원을 가지기 때문에 임의의 주행환경에서 동력원들의 동력을 분배하는 방식에 따라서 하이브리드 차량의 연비효율이 큰 차이를 보이게 된다. 이와 같이 하이브리드 차량의 동력분배 전략은 하이브리드 차량의 연비효율에 가장 많은 영향을 미치는 요인 중 하나이기 때문에 그 동안 많은 연구가 진행되어 왔다. 동력분배전략의 대표적인 접근방식에는 동적계획법(Dynamic programming) 기반의 동력분배전략,2,3) Pontryagin’s minimum principle (PMP) 기반의 동력분배전략,4,5) 그리고 강화학습 기반의 동력분배전략6,7)이 있다.
동적계획법은 전역 최적해를 보장한다는 장점이 있으나 많은 연산량을 필요로 하고 미래의 주행정보가 주어져야만 한다는 단점을 가진다. 미래의 주행정보에 대한 필요성으로 인하여 동적계획법 기반의 동력분배전략은 실제 차량에 직접적으로 적용되기 어렵고 동적계획법은 주로 하이브리드 차량의 단품의 용량을 설계하거나 개발된 동력분배전략의 유효성 검증에 필요한 기준점을 도출할 때 활용된다.
PMP 기반의 동력분배전략에서는 설정된 Hamiltonian을 최소화 하는 방식으로 에너지 관리가 이루어진다. 주로 Hamiltonian은 연료소모율과 배터리파워를 고려하여 설계되는데, 배터리파워는 일종의 등가화 계수인 Co-state를 통해서 연료소모율로 등가화된다. 초기 Co-state가 적절히 설계 될 경우, PMP 기반의 동력분배전략은 동적계획법 기반의 동력분배전략에 상응하는 연비효과를 도출할 수 있다.3) 하지만 최적 Co-state는 미래의 주행환경에 의존적이기 때문에 실제 차량에 적용하기 어려운 점이 존재한다. 최근에는 미래의 주행정보를 예측하여 최적의 Co-state를 도출하고자 하는 연구가 진행되고 있다.8)
강화학습 기반의 동력분배전략에서는 현재의 State를 통해서 하이브리드 차량의 에너지 관리를 수행한다. 따라서 강화학습 기반의 동력분배전략은 미래의 주행정보를 필요로 하지 않기 때문에 실제 차량에 개발된 동력분배전략을 적용하기 수월하다. 최근에는 강화학습 과 심층인공신경망(Deep neural network)을 융합한 형태의 Deep Q-networks(DQN)이 개발되어 강화학습 분야에 혁신을 불러일으켰다.9,10) DQN은 매우 복잡한 문제를 효과적으로 해결할 수 있음이 많은 연구 등을 통해서 입증되고 있다.
이에, 본 연구에서는 하이브리드 전기자동차 실제 차량에 적용하기가 용이하면서 효율적인 동력분배가 가능한 DQN 기반의 동력분배전략을 개발하고자 하며, 최적 Co-state가 주어진 PMP 기반의 동력분배전략과 비교하여 그 성능을 검증하고자 한다.
2. 연구 배경
본 파트에서는 강화학습의 일종인 Q-learning과 DQN에 대해서 개략적인 설명을 진행한다. Q-learning에서는 목적함수의 일종인 Q-value를 최대화하는 Policy를 구성하는 방법론을 제공하며 DQN은 Q-learning의 이론적인 배경에 심층인공신경망을 적용하여 매우 복잡한 문제를 효과적으로 해결할 수 있는 방법론을 제공한다.
2.1 Q-learning
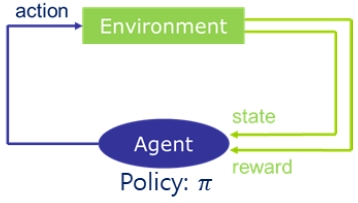
강화학습의 일종인 Q-learning은 Fig. 1과 같은 마르코프 프로세스(Markov decision process, MDP)를 기반으로 수학적으로 표현된다. MDP에는 두 가지 성분이 존재한다. 하나는 Environment이며 다른 하나는 Agent이다. Environment는 Agent에서 도출된 Action에 따른 State와 Reward를 Agent에 전달하고, Agent는 Environment로부터 전달받은 State와 내부의 구성된 Policy를 통해서 Action을 도출한다.
즉, Q-learning은 현재 State로부터 Action을 맵핑하는 Policy를 도출할 수 있는 방법론을 제공한다. Q-learning의 목적은 Q-value를 최대화하는 Policy를 도출하는 것에 있다. Q-value는 식 (1)과 같이 Reward를 누적시킨 총합으로 표현된다. ρ는 Discount factor로써, 0과 1사이의 값을 가진다. ρ가 0에 가까울수록 현재 시점의 Reward가 Q-value에서 차지하는 비중이 높아지고 반대로 ρ가 1에 가까울수록 현재 시점의 reward는 Q-value에서 차지하는 비중이 낮아진다.
Q-learning은 식 (2)와 같이 Q-value를 최대화하는 Policy π를 도출하는 것을 목표로 삼는다. Q-learning에서는 Q-value를 State와 Action에 따른 Q-value를 저장하는 테이블의 형식의 Q-table을 기반으로 Policy가 구성된다. 그리고 Q-table 내의 Q-value는 식 (3)과 같이 Bellman optimality equation을 통해서 반복적으로 업데이트된다.
| (1) |
where Rt : reward
ρ : discount factor
s : state
a: action
| (2) |
where π : policy
| (3) |
where s′ : next state
a′ : action for the next state
2.2 Deep Q-Networks
Q-learning은 State와 Action에 따른 Q-value를 테이블 형식의 Q-table을 통해서 Policy를 도출하기 때문에 과도한 State가 주어지는 복잡한 문제에 대해서는 불안정한 학습과정을 겪게 된다. 즉, 과도한 State의 차원이 존재하는 경우에는 차원의 저주문제(Curse of dimensionality problem)로 인해서 학습속도가 매우 느려지고 Sparse Q-table이 도출되는 등의 문제가 발생하게 된다.
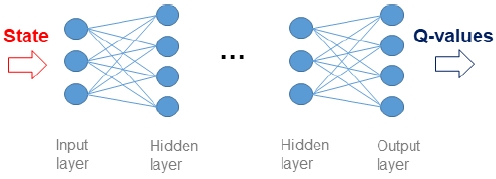
이러한 기존의 Q-learning에 대한 문제는 Q-learning에 심층인공신경망을 도입한 형태의 Deep Q-networks(DQN)를 통해서 효과적으로 해결되었다.8) 아래의 Fig. 2와 같은 심층인공신경망의 Input layer는 연속적인 값(Continuous value) 형식의 State가 입력받고 Hidden layer를 통해서 State에 대한 Feature가 생성된다. 그리고 최종적으로 Output layer에서는 Action에 따른 Q-value의 추정 값이 도출된다. 따라서 Input layer의 유닛의 개수는 State의 차원과 동일하고 Output layer의 유닛의 개수는 Action의 차원과 동일하다. DQN내 심층인공신경망의 Input layer에서는 State가 이산화 된 값의 형식이 아닌 연속적인 값의 형식으로 입력되기 때문에 DQN은 차원의 저주문제를 효과적으로 해결할 수 있고 그로인해 State의 수가 매우 많은 복잡한 문제에 대해 적용이 가능하다.
본 연구에서는 Q-learning과 심층인공신경망을 결합한 DQN을 활용하여 실차적용성이 높고 효율적인 하이브리드 차량의 동력분배전략을 개발하는 연구를 진행하였다.
3. DQN 기반의 동력분배전략의 개발
본 연구에서는 병렬형 하이브리드 차량을 대상으로 한 동력분배전략을 개발하였다. 본 파트에서는 연구 대상 차량의 사양과 DQN의 학습과정에 대해서 간략한 소개한다.
3.1 연구대상 차량모델
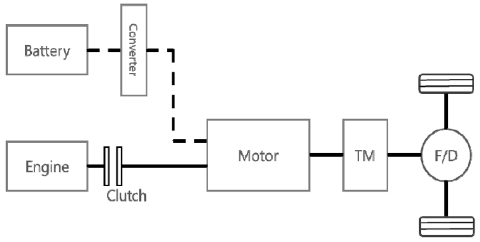
본 연구에서는 연구대상 차량을 Fig. 3과 같은 구조를 가지는 병렬형 하이브리드 차량으로 삼아서 연구를 진행하였다. 초기 배터리 State of charge(SOC)와 최종 상태에서 목표로 하는 Target SOC는 0.6으로 설정하였다. 연구대상차량은 엔진 앞에 클러치를 통해서 엔진 동력의 전달을 조절하며 6속의 자동변속기를 탑재하고 있다. 차량모델에 대한 상세한 사양은 Table 1에 표현되어 있다.
3.2 State, Action, Reward에 대한 정의
강화학습 분야에서 State, Action, 그리고 Reward에 대한 설계는 Agent의 성능을 결정하는 매우 중요한 요소이다. 본 파트에서는 State, Action, 그리고 Reward를 정의한 방식에 대해서 간략히 소개한다.
State는 Agent가 Action을 도출하는 데, 필요한 입력정보로 본 연구에서는 SOC 변화량, 요구파워, 그리고 차량속도를 State의 요소로 고려하였다. SOC 변화량은 식 (4)처럼 현재 SOC와 초기 SOC의 차이로 정의된다.
| (4) |
Action은 임의의 State가 주어졌을 때, Agent가 구성된 Policy에 따라 Environment에 전달하는 행위이다. 임의의 State에 대해서 적절한 Action이 취해졌을 시, Agent는 Environment로부터 많은 Reward를 획득 할 수 있고 반대의 경우엔 적은 Reward를 획득하게 된다.
본 연구에서는 Action을 하이브리드차량의 엔진토크로 정의하였다. Action set의 크기는 10개이며 수학적으로는 아래의 식 (5)처럼 표현할 수 있다. Action set의 각각의 요소는 0부터 최대엔진 토크를 선형적으로 나눈 값이다.
| (5) |
where Tmax : maximum engine torque
Reward는 Agent가 학습되어야할 학습방향을 암시하는 수학적인 표현이다. 따라서 Reward의 설계는 강화학습 분야에서 가장 중요한 요소이며 적절한 Reward의 설계가 되지 못하면 좋은 성능의 Agent를 도출하는 것은 불가능하다.
본 연구에서는 PMP에서의 Hamiltonian과 유사하게 식 (6)과 같이 화학적 에너지와 전기적 에너지의 소모량을 고려한 Reward를 고려하였으며 전기적 에너지는 등가계수 ψ를 통해서 화학적 에너지로 등가화 된다. PMP의 Hamiltonian과 본 연구의 DQN 모델에서 활용한 Reward는 모두 화학적 에너지와 전기적 에너지를 등가화 하는 일종의 등가계수가 존재하는데, PMP에서는 이를 Co-state라고 한다. Co-state는 PMP이론에 따라 각 Step별로 업데이트되므로 초기 Co-state를 어떻게 설정하느냐에 따라서 PMP 성능이 결정된다. 즉, PMP의 성능은 주행사이클에 따라 초기 Co-state를 어떻게 설정하느냐에 따라서 결정되는 값으로, 미리 주행정보를 알고 있을 시에만 최적의 Co-state를 도출할 수 있다. 반면, 본 연구에서의 Reward에서 활용되는 등가계수 ψ는 주행사이클에 의존적인 값이 아니라 화학적 에너지와 전기적 에너지를 등가화하는 임의적인 값이다.
그리고 ψ는 식 (7)에서처럼 ∆SOC의 함수로 표현되고 ψ는 ∆SOC에 비례하도록 설계되었다. 식 (7)과 같이 등가계수가 ∆SOC에 비례하도록 설정한 이유는 차량의 Charge sustain 성능을 확보하기 위해서이다. 현재 SOC가 초기 SOC와의 차이가 클 경우, 등가계수의 영향으로 인하여 전기적 에너지가 전체 Reward에 미치는 영향이 커지게 되고 이로 인해 Agent는 전기적 에너지보다는 화학적 에너지를 적극적으로 사용함으로써 초기 SOC와의 과도한 차이가 나지 않게 동력분배를 수행하도록 학습이 된다.
| (6) |
where Eche : chemical energy
Eelec : electric energy
| (7) |
이와 같이, 본 연구에서 위와 같은 Reward를 설계함으로써 기본적으로는 화학에너지와 전기에너지를 최소화하는 Policy를 구성하도록 Agent를 유도하였으며 등가계수 ψ를 ∆SOC의 함수로 표현하여 결국 Final state에서의 SOC가 Target SOC와 큰 차이를 보이지 않도록 Reward를 설계하였다.
3.3 Deep Q-Networks의 학습 과정
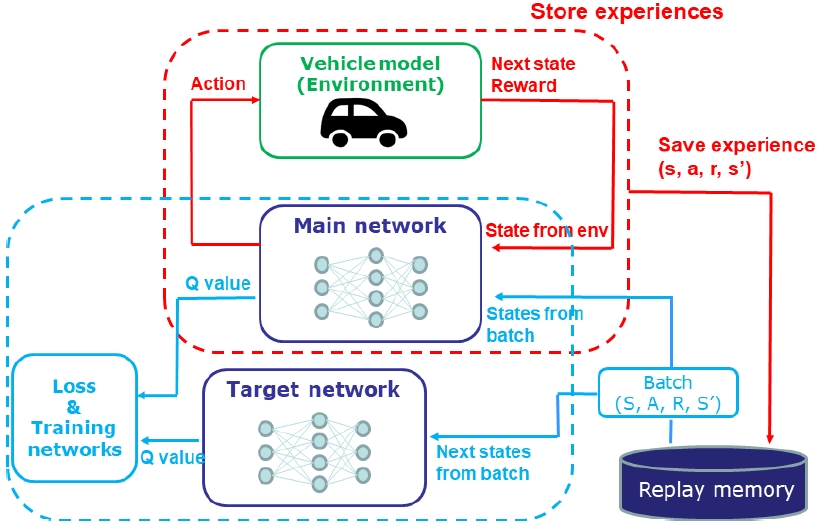
DQN은 두 가지 프로세스을 거쳐서 학습이 이루어진다. 하나는 Agent의 Experience을 저장하는 프로세스이고 나머지 하나는 DQN에 존재하는 두 개의 심층인공신경망의 학습이 이루어지는 프로세스이다. Fig. 4는 DQN의 학습과정에 대한 개략적인 모형을 보여준다. 하이브리드 차량의 동력분배전략 개발에 대한 DQN 모델에서 Environment는 하이브리드 차량에 대응되며 Agent는 심층인공신경망을 통해서 추측된 Q-value를 기반으로 Action을 취한다.
Experience를 저장하는 프로세스에서는 Agent가 반복적인 학습과정에서 겪게 되는 Experience를 Replay memory라고 하는 저장소에 저장하게 된다. Experience는 현재 State, Action, Reward, 그리고 다음 Staet로 이루어진 튜플 형식의 데이터이다. Experience는 학습과정에서 지속적으로 Replay memory에 저장되고 Replay memory에 저장된 Experience들은 DQN의 두 개의 네트워크를 학습시키는 데, 활용된다.
그리고 학습 프로세스에서는 DQN내의 두 개의 네트워크의 학습이 이루어진다. DQN에는 Main network와 Target network가 존재하는데, Main network는 Q-value를 추측하여 Agent의 Action을 결정하는 역할을 하고 Target network는 식 (8)과 같이 Target Q-value를 도출한다.
| (8) |
where θ′ : weights in the target network
Main network 학습에 필요한 손실함수 L는 식 (9)와 같이 Main network에서 도출된 Q-value와 Target network에서 도출된 Target Q-value의 Mean squared error(MSE)로 정의된다.
| (9) |
where θ : weights in the main network
학습과정에서 두 네트워크에 존재하는 다수의 Weight는 역전파 알고리즘(Back-propagation algorithm)을 기반으로 식 (9)에서 정의된 손실함수를 최소화하는 방향으로 조정된다.
4. 시뮬레이션 조건 및 결과
Main network와 Target network의 구조는 동일하며 네트워크 구조에 대한 정보는 Table 2에 나타나 있다. Input layer의 유닛의 개수는 State의 차원의 개수와 동일한 3개이며 각각의 유닛은 각각의 State의 요소(요구파워, 차량속도, SOC 차이)에 대한 연속적인 값을 입력받게 된다. 이후의 두 개의 Hidden layer의 유닛의 개수는 각각 64개와 128개이다. 그리고 심층인공신경망에 비선형적인 특성을 부여하는 Hidden layer의 Activation function은 Rectified linear unit(ReLU)로 설정하였다. 마지막으로 Output layer에서의 유닛의 개수는 Action의 크기와 동일하므로 10개이고 각각의 유닛은 유닛에 해당되는 Action의 Q-value를 도출하게 된다.
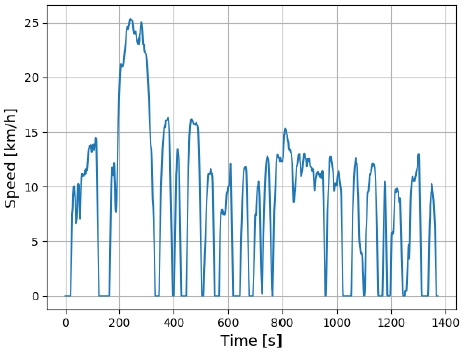
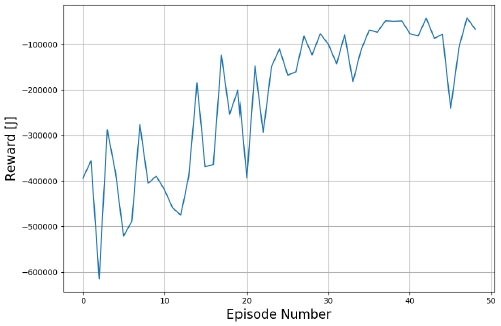
본 연구에서는 개발한 DQN 기반의 동력분배전략의 유효성을 검증하기 위해서 최적 Co-state가 주어진 경우에서의 PMP 기반의 동력분배전략과 비교되었다. DQN 기반의 동력분배전략은 Fig. 5와 같은 FTP-72 사이클 상에서 학습을 진행하였다. Fig. 6은 학습 진행에 따른 Reward의 누적 값에 대한 변화를 보여주고 있다. Fig. 6의 x축은 에피소드의 횟수를 의미하며 y축은 누적 Reward로써 [J]의 단위를 가진다. 에피소드란 DQN이 주기적인 학습 사이클을 의미하며, 본 연구에서는 학습에 활용된 주행 사이클인 FTP-72 완주하여 학습이 마무리되는 순간을 하나의 에피소드로 규정하였다. Fig. 6을 통해서 학습 에피소드가 증가함에 따라서 Agent는 주어진 State 상에서 점점 더 많은 Reward를 추구하는 쪽으로 Action을 취하는 경향성을 보임을 알 수 있다.
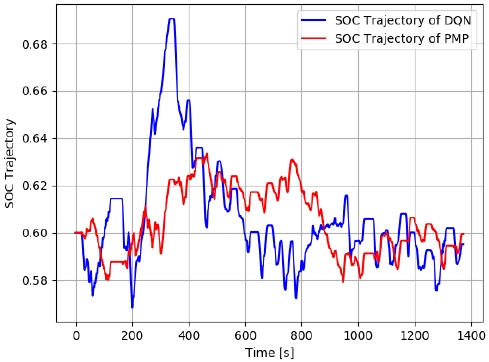
Table 3은 FTP-72 사이클에서 PMP 기반의 동력분배전략의 시뮬레이션 결과와 DQN 기반의 동력분배전략을 비교한 결과를 보여준다. 그리고 Fig. 7은 FTP-72 주행 사이클 상에서의 DQN 제어전략 기반의 SOC 경로와 PMP 제어전략 기반의 SOC 경로를 보여준다. Fig. 7을 보면 DQN기반의 제어전략의 경우 최종 SOC가 초기 SOC인 0.6에 유사하게 유지됨을 볼 수 있는 데, 이는 DQN 제어전략을 통해서 Charge sustain 능력이 확보할 수 있음을 볼 수 있다. 다만 DQN 기반의 제어전략은 200초에서 800초에 걸쳐 과도한 충방전이 이루어져 PMP의 SOC 경로와 상당히 큰 괴리를 보이는데, 이러한 현상이 DQN 기반의 제어전략이 PMP기반의 제어전략에 비해서 연비가 떨어지는 요인으로 작용했을 것으로 예상된다. DQN 기반의 제어전략은 최적 Co-state가 주어진 상황에서의 PMP 기반의 제어전략과 비교하여 연비가 약 6 %정도 낮으며 등가화 된 연료소모율 측면에서는 약 7 %정도 낮음을 확인하였다. 등가화 된 연료소모율은 최종 SOC를 고려한 연료소모율을 의미한다.
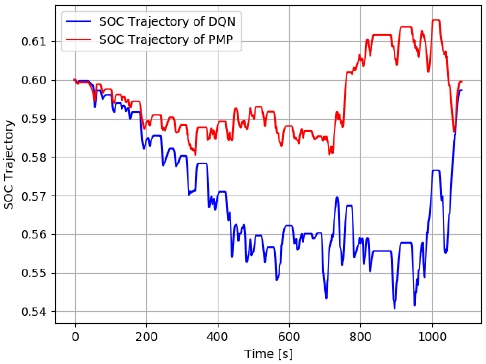
그리고 DQN 기반 제어전략의 일반화된 성능을 알아보고자 Table 4와 같이 학습에서 사용되지 않은 주행 사이클인 Nuremberg 주행사이클에 대한 DQN과 PMP 제어의 성능비교를 비교하였다. 그리고 Fig. 8은 Nuremberg 주행사이클에서의 DQN과 PMP 기반 제어전략의 SOC 경로를 보여준다. 학습에서 활용되지 않은 사이클 상에서도 DQN기반의 동력분배전략은 초기 SOC와 최종 SOC의 차이가 0.03에 불과한 점을 볼 때, Charge sustain 성능에 대한 일반화가 이루어졌다고 볼 수 있다. 다만, Table 4 에서 확인할 수 있듯이 Nuremberg 주행사이클은 학습에서 활용된 주행사이클이 아니기 때문에 Nuremberg 주행사이클에서의 DQN의 SOC 경로와 PMP의 SOC 경로의 차이는 학습에 활용된 FTP-72 사이클에서의 DQN의 SOC 경로와 PMP의 SOC 경로의 차이보다 크다. 이로 인해 DQN 기반의 동력분배 전략의 경우, Nuremberg 주행사이클에서의 연비가 FTP-72 주행사이클에서의 연비보다 상대적으로 낮음을 Table 4를 통해서 알 수 있다.
본 연구를 통해서 개발된 DQN 기반의 동력분배전략은 실차적용 가능성에 핵심적인 성능인 Charge sustain 능력을 확보할 수 있음을 확인하였다. 최적 Co-state가 보장된 PMP 기반의 제어전략의 결과는 전역 최적해를 보장하는 동적계획법 기반결과와 매우 유사하다는 사실을 고려할 때, DQN 기반의 동력분배전략의 결과는 최적해와 유사한 결과를 얻을 수 있음을 확인하였다.
5. 결 론
본 연구에서는 DQN 기반의 하이브리드차량의 동력분배 전략을 개발하였다. DQN 기반의 동력분배전략은 강화학습 기반의 동력분배전략으로써, DP나 PMP 기반의 동력분배전략과 달리 미래의 주행정보를 필요로 하지 않는다는 점에서 실차적용성이 높다. 그리고 DQN 모델은 기존의 Q-learning 모델에 심층인공신경망을 도입하여 차원의 저주의 문제로부터 자유로울 수 있다는 장점이 있다.
본 연구에서는 위와 같은 DQN 모델의 장점을 활용하여 하이브리드차량의 동력분배전략을 개발하고 그에 대한 유효성을 PMP 기반의 동력분배전략과 비교하였다. 비교 결과, 개발된 DQN 모델은 최종 SOC를 초기 SOC로 유지하는 Charge sustain 능력이 확보될 수 있음을 확인하였다. 그리고 학습 데이터로 활용된 FTP-72 사이클상에서 DQN 모델은 연비효율 측면에서 최적화된 PMP 결과와 약 6 %의 차이를 보였으며 학습에 활용되지 않은 Nuremberg 주행사이클 상에서 DQN 모델은 PMP 결과와 약 13 %의 연비차이를 보였다. 학습되지 않은 주행사이클 상에서의 DQN 기반의 제어전략은 PMP 기반의 제어전략과 다소 높은 연비 차이를 보이는 데, 이는 DQN 기반의 제어전략의 일반화 성능이 높지 않다는 것을 의미한다. 향후 연구에서는 학습 데이터의 다양성과 크기를 증가시켜서 DQN 모델의 일반화 성능을 강화시킬 예정이다.
Nomenclature
| s : | state |
| r : | reward |
| a : | action |
| s’ : | next state |
| π : | policy |
| ρ : | discount factor |
Subscripts
| θ : | weights for main network |
| θ ’ : | weights for target network |
References
-
S. Kim, W. S. Choi, M. Kim, H. Kim and W. Lim, “Analysis of Fuel Economy of Mild Hybrid Vehicle by the Backward Simulation with Considering Power Loss of Oil Pump,” Transactions of KSAE, Vol.26, No.4, pp.533-539, 2018.
[https://doi.org/10.7467/KSAE.2018.26.4.533]

-
Y. Yang, X. Hu, H. Pei and Z. Peng, “Comparison of Power-split and Parallel Hybrid Powertrain Architectures with a Single Electric Machine: Dynamic Programming Approach,” Applied Energy, Vol.168, pp.683-690, 2016.
[https://doi.org/10.1016/j.apenergy.2016.02.023]

-
J. Kim and Y. I. Park, “Fuel Economy Analysis of Novel Hybrid Powertrain for PHEV,” Transactions of KSAE, Vol.27, No.4, pp.325-332, 2019.
[https://doi.org/10.7467/KSAE.2019.27.4.325]

-
N. Kim, S. W. Cha and H. Peng, “Optimal Control of Hybrid Electric Vehicles based on Pontryagin’s Minimum Principle,” IEEE Transactions on Control Systems Technology, Vol.19, No.5, pp.1279-1287, 2011.
[https://doi.org/10.1109/TCST.2010.2061232]

-
C. H. Zheng, G. Q. Xu, S. W. Cha and Q. Liang, “Numerical Comparison of ECMS and PMP-based Optimal Control Strategy in Hybrid Vehicles,” Int. J. Automotive Technology, Vol.15, No.7, pp.1189-1196, 2014.
[https://doi.org/10.1007/s12239-014-0124-5]

-
X. Lin, Y. Wang, P. Bogdan, N. Chang and M. Pedram, “Reinforcement Learning based Power Management for Hybrid Electric Vehicles Categories and Subject Descriptors,” Proceedings of the 2014 IEEE/ACM International Conference on Computer-Aided Design, pp.32-38, 2014.
[https://doi.org/10.1109/ICCAD.2014.7001326]

-
Y. Zou, T. Liu, D. Liu and F. Sun, “Reinforcement Learning-based Real-time Energy Management for a Hybrid Tracked Vehicle,” Applied Energy, Vol.171, pp.372-382, 2016.
[https://doi.org/10.1016/j.apenergy.2016.03.082]

-
S. Xie, X. Hu, Z. Xin and J. Brighton, “Pontryagin’s Minimum Principle based Model Predictive Control of Energy Management for a Plug-in Hybrid Electric Bus,” Applied Energy, Vol.236, pp.893-905, 2019.
[https://doi.org/10.1016/j.apenergy.2018.12.032]

-
V. Mnih, K. Kavukcuoglu, D. Silver, A. Rusu, J. Veness, M. G. Bellemare, A. Graves, M. Riedmiller, A. K. Fidjeland, G. Ostrovski, S. Petersen, C. Beattie, A. Sadik, I. Antonoglou, H. King, D. Kumaran, D. Wierstra, S. Legg and D. Hassabis, “Human-level Control Through Deep Reinforcement Learning,” Nature, Vol.518, pp.529-533, 2015.
[https://doi.org/10.1038/nature14236]

-
D. Silver, A. Huang, C. J. Maddison, A. Guez, L. Sifre, G. Driessche, J. Schrittwieser, I. Antonoglou, V. Panneershelvam, M. Lanctot, S. Dieleman, D. Grewe, J. Nham, N. Kalchbrenner, I. Sutskever, T. Lillicrap, M. Leach, K. Kavukcuoglu, T. Graepel and D. Hassabis “Mastering the Game of Go with Deep Neural Networks and Tree Search,” Nature, Vol.529, pp.484-489, 2016.
[https://doi.org/10.1038/nature16961]