메타분석기반 자동비상제동장치 사고방지 효과 연구
Copyright Ⓒ 2019 KSAE / 167-09
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
For the road safety of passengers and vulnerable road users, the advanced driver-assistance systems(ADAS) were recently introduced in vehicles. Among the ADAS, AEB is known as the best safety device for preventing traffic accidents. However, it is difficult to find a study that analyzes its effects by using the accident statistics of a country. The effectiveness of AEB on actual roads is the basic data for improving the performance of AEB and calculating the vehicle insurance premium. This paper presents the collision avoidance effect of AEB by means of a meta-analysis method. Meta-analysis is a statistical method used for deriving a comprehensive conclusion based on several studies. In order to estimate the effectiveness of AEB by applying the meta-analysis method, the accident data from Korean auto insurance companies are used. As a result, among the same model vehicles, the accident rate of a vehicle with an AEB was approximately 10 % to 17 % smaller than that of a vehicle without an AEB. The purpose of this study is to verify the effectiveness of AEB’s actual accident prevention for domestic vehicles lacking in statistical verification studies.
Keywords:
ADAS, AEB, Meta-analysis, IVW, WLS키워드:
첨단운전자지원장치, 자동비상제동장치, 메타분석, 역분산가중추정법, 가중최소제곱추정법1. 서 론
현재 세계 자동차산업의 가장 큰 화두는 자율주행차이다. 보행자와 자동차 탑승자의 완벽한 안전을 담보하면서 운전자의 조작이 전혀 필요하지 않은 완전자율주행을 달성하기 위하여 전 세계 자동차 제작사와 관련 IT 업체들이 연구에 매진하고 있다. 이 과정에서 완전자율주행 이전 단계로 차량 사고를 막고 운전자에 편의를 제공하는 안전장치들이 차량에 장착되고 있다. 전방 차량, 보행자 등을 인식하여 충돌 이전에 경고하거나 제동을 통해 사고를 방지하는 전방충돌경고장치(FCW, Forward Collision Warning System)와 자동비상제동장치(AEB, Autonomous Emergency Braking System), 차선이탈을 경고하거나 방지하기 위한 차선이탈경고장치(LDWS, Lane Departure Warning System)와 차선유지지원장치(LKAS, Lane Keeping Asist System) 등을 첨단운전자지원장치(ADAS, Advanced Driver Asistance Systems)라고 부른다. ADAS가 빠른 속도로 보급됨에 따라, 해당 장치들의 성능을 연구하고 장착효과를 추정하는 일도 중요한 작업으로 대두되었다. 미국 고속도로안전보험연구소(IIHS, Insurance Institue for Highway Safety)는 ‘City Safety’라고 명명한 Volvo社의 AEB장치를 장착한 차량과 미장착된 타사의 유사 차량과 비교했을 때 사고 발생 비율이 14 % 감소하는 것을 확인했으며, 추돌사고의 경우 그 수치가 무려 41 %나 된다고 분석하였다.1) 우리나라에서도 자동차 제작사, 기관, 학계 주도로 ADAS의 성능 평가를 위한 연구가 지속적으로 수행되고 있다. 보험개발원 부설 자동차기술연구소에서는 정지한 차량 및 움직이는 보행자 타겟을 대상으로 AEB의 충돌방지 성능평가를 실시했으며, 차량별로 상이한 충돌 회피 성능을 나타냈다고 보고했다.2) 또한 대구경북자동차부품진흥재단에서는 움직이는 무인타겟차량(Unmaned Target Vehicle)을 이용하여 Lane Change Test를 실시하였으며, Euro NCAP의 AEB City/Urban/Pedestrian 시험 절차에 따라 다양한 시나리오를 적용하여 시험평가기술개발을 진행 중이다.3) 그러나 데이터집적과 같은 문제 등으로 인해 실도로에서 나타나는 ADAS 장치들의 장착효과를 추정하기 위한 연구는 수행하기 어려운 실정이다. 그럼에도 불구하고 ADAS 개발 방향, 시험평가기술개발, 자율주행차량 및 자동차보험 정책 방향 설정 등에는 실제 사고 데이터에 기반 한 성능평가가 반드시 필요하다.
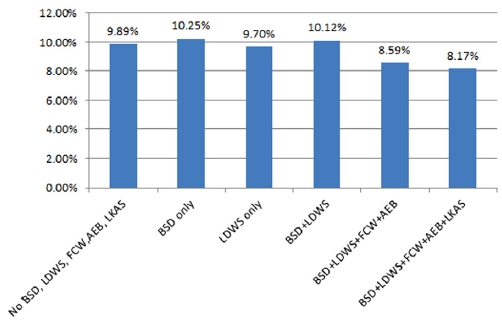
본 연구를 위한 선행연구로 국내 자동차보험사로부터 수집한 자동차보험 계약정보 및 사고정보 데이터를 이용하여 중복 장착되는 경우가 많은 ADAS 장치별 사고방지 효과를 비교하였다. 사용 데이터는 2014~2017년 자동차보험 통계이며 BSD/LDWS/FCW/AEB/LKAS를 모두 장착하지 않은 트림, BSD만 장착한 트림, LDWS만 장착한 트림, BSD 및 LDWS를 장착한 트림, BSD/LDWS/FCW/AEB를 장착한 트림, BSD/LDWS/FCW/AEB/LKAS를 모두 장착한 트림별로 대물배상담보에 대한 사고율을 비교하였다. 분석에 사용된 전체 트림은 101개이며 5개의 장치를 1개 이상 기본 장착한 트림을 기준으로 각 장치별 기본장착, 선택장착, 미장착 트림을 구분하여, 장치별 57,280~85,699개의 데이터 세트를 마련하였다. 장착 여부가 불명확한 선택장착 트림을 제외한 후, 기본장착 및 미장착 트림 데이터를 이용하여 카테고리별 사고율을 다변량 분석 방법으로 분석하였다. 그 결과 Fig. 1과 같이 5개 장치가 모두 장착되지 않은 카테고리의 사고율 9.89 %에 비해 BSD/LDWS 장착 카테고리는 10.12 %로 다소 높았고, BSD/LDWS/FCW/AEB를 장착한 카테고리는 사고율이 8.59 %로 나타나, AEB(FCW포함) 장치 장착에 따른 효과가 가장 큰 것으로 나타났다.
Fig. 1의 결과를 바탕으로 ADAS 장비 중 사고율 감소 효과가 가장 크다고 판단되는 AEB/FCW(분석대상 모든 차량이 AEB 장착 시 FCW가 기본 장착되어, 이후 AEB로 통칭) 장치에 대해 교통사고 예방 및 경감 효과를 추정하는 하는 연구를 실시하였다. 특히 기존 연구와 달리, 동일 차량모델을 AEB 장착 여부로 구분한 후 데이터를 수집하고 메타분석을 적용함으로써 차량모델에 의한 변동을 최소화하고 추정 정확도를 증가시켰다.
2. 메타분석
2.1 기존 연구
본 연구에서는 차량에 장착된 AEB의 사고방지효과를 종합하기 위해 메타분석 방법을 사용하였다. 메타분석은 다수의 연구결과를 바탕으로 하나의 종합적인 결론을 도출할 때 사용하는 통계적 기법이다. 지속가능한 체계적 고찰의 구체적인 방법론 중 하나인 메타분석은 의학(또는 약학) 분야에서 동일하거나 유사한 주제로 실시된 연구결과들을 결합하여 논리적 결론을 내리기 위한 방법으로 주로 사용되었다. 1904년 Pearson에 의해 처음으로 의학 연구결과들이 결합되기 시작하였고,4) 1976년 Glass에 의해 ‘메타분석’이라는 용어가 처음으로 사용되었다.5) 스코틀랜드 태생의 의학자 Cochrane은 약 3,500여 개의 자료를 결합하여 600여개의 종합된 연구결과를 발표하였고,6,7) 이는 체계적 고찰이 발전하는 토대가 되었다. 메타분석을 포함한 체계적 고찰 연구방식의 사용은 90년대 이후 전 세계적으로 급증하고 있으며, 의학분야의 경우 세계적으로 출간되는 논문 중 약 1.5 %가 이 방법을 사용하고 있을 정도로 관련분야의 중요한 연구영역으로 자리 잡았다.8) 메타분석은 교통사고 통계적 연구분야에서도 다양하게 활용되고 있다. Elvik은 메타분석을 활용하여 사고의 심각도, 도로의 종류, 국가, 연도 등에 따른 교통 정온화(Traffic calming) 수단의 효과를 추정하였고,9) Caird 등은 운전 중 전화사용이 운전자의 반응속도에 미치는 영향을 연구한 논문들을 결합하여 종합적인 결론을 도출하는데 메타분석을 사용하였다.10) 또한 IIHS는 미국 자동차보험 데이터에 메타분석 방법론을 적용하여 Volvo차량에 장착된 AEB의 사고경감효과를 유사 차종과 비교하여 추정하였다.11) 본 연구에서는 국내 11개 손해보험사로부터 확보한 자동차보험 데이터에 메타분석 방법을 적용하여 국내 5개 자동차 제작사가 차량에 장착하고 있는 AEB 장치의 사고감소효과를 추정하였다.
2.2 교차비 (Odds ratio)
본 연구에서는 AEB장비가 장착되지 않은 차량(대조군)과 AEB장비가 기본으로 장착된 차량(처리군)의 비교를 위한 요약척도로 교차비를 사용하였다. 개별 차량모델에 장착된 AEB의 사고감소효과를 교차비를 통해 계산하고 이를 다시 종합하는 방식으로 연구를 진행하였다. 개별 차량모델에 장착된 AEB의 사고감소효과는 다음과 같이 교차비 형태로 정의할 수 있다.12)
여기서 nci는 조사기간 내 전체 대조군 차량의 국내 운행대수 값을, xci는 조사기간의 대조군 차량의 사고 발생건수를 의미한다. 이와 유사하게 nti는 조사기간 내 전체 처리군 차량의 국내 운행대수 값을, xti는 처리군 차량의 사고 발생건수를 의미한다(단, 본 연구에서는 운행대수의 값을 보험계약일로부터 추정한 , 값을 사용하였다). 만약 대조군과 처리군의 사고 발생률이 동일하다면 상기 교차비(ORi) 값은 1.0이 된다. 또한 ORi 값이 1.0보다 작을 경우 해당 차량에 장착된 AEB는 사고감소에 효과가 있는 것을 의미한다. 반대로 ORi 값이 1.0보다 크거나 같은 경우에는 차량에 장착된 AEB는 사고발생 감소에 효과가 없는 것을 의미한다.
2.3 고정효과모형과 변량효과모형
개별 차량모델의 AEB 사고감소효과를 결합하기 위하여 본 연구에서는 역분산가중추정법(IVW, Inverse variance weighted estimation method)과 가중최소제곱추정법(WLS, Weighted least squares estimation method) 두 가지를 사용하였다. 고정효과모형의 하나인 역분산가중추정법은 처리효과는 모두 동일하나, 개별연구에서 사용된 표본들을 추출하는 과정에서 변동이 발생하여 다른 결과가 도출된다는 가정이다. 즉, AEB 장착효과 자체는 모든 차량에서 동일하나 운전자, 사고발생 위치나 환경 등의 변동이 발생하여 다른 효과를 나타낸다는 이론이다. 반대로 가중최소제곱추정법은 변량효과모형의 하나로 개별연구들이 갖는 서로 다른 특성을 인정하고 표본추출변동과 개별 연구의 처리효과 변동을 함께 고려하여 종합적인 결론을 내는 방법이다. 즉, 차량모델 별로 장착된 AEB가 모두 다른 장착효과를 가지며, 이를 고려하여 차량모델에 따른 특성과 앞서 언급한 외부 환경적인 요소를 모두 고려하여 AEB 장착효과를 추정하는 이론이다.13)
본 연구에서는 두 가지 결합방법을 모두 사용하여 자동차보험데이터를 분석하고, 그 결과를 토대로 국내 시판중인 차량에 장착된 AEB 장치의 사고감소효과에 대해 논리적 결론을 도출하였다.
임의의 k개 연구에 대하여, 고정효과모형을 사용하면 개별연구의 효과는 다음과 같이 나타낼 수 있다.
이때 θi는 처리효과(본 연구에서는 AEB 장착으로 인해 발생하는 사고감소효과)를 나타내고, ei는 개별연구가 가지는 표본추출로부터의 변동을 의미하며 일반적으로 평균이 0이고 분산이 인 정규분포를 가정한다. 고정효과모형에서는 개별연구에 관계없이 처리효과가 동일한 것으로 가정하므로 θi는 임의의 값 μ와 같다고 나타낼 수 있다. θi=μ(단, i=1,2,...,k)로 표현할 수 있으며, 공통된 처리효과를 추정하기 위해서 μ값에 대해 적절한 추정치를 역분산가중추정법으로 도출하면 된다.
역분산가중추정법은 개별연구에 의한 변동을 분산의 역수를 가중치로 하여 가중평균을 구하는 것과 같다. 역분산가중추정법에 사용하는 개별연구들의 가중치()는 개별연구 표본의 크기로부터 결정되며 아래와 같이 구할 수 있다.
여기서 yi는 개별 차량모델의 AEB 사고감소 효과, 는 yi 변동(분산)의 추정 값을 나타낸다. 앞서 교차비에서 설명한 것과 같이 xti는 처리군 차량의 사고 발생건수, xci는 조사기간의 대조군 차량의 사고 발생건수, 는 조사기간 내 전체 처리군 차량의 국내 운행대수 값을 보험계약일로부터 추정한 값, 는 조사기간 내 전체 대조군 차량의 국내 운행대수 값을 보험계약일로부터 추정한 값이다.
결과적으로, 역분산가중추정법(IVW)을 통하여 획득한 처리효과의 교차비는 다음과 같은 형태로 표현된다.
변량효과모형은 개별연구에서 발생하는 처리효과가 서로 다름을 가정하므로, 변량효과모형을 사용하여 개별연구의 효과를 나타낼 경우 다음과 같이 표현될 수 있다.
(단, ei와 ϵi는 서로 독립)
고정효과모형과는 다르게, 변량효과모형에서는 처리효과 θi도 평균이 0이고 분산이 τ2인 정규분포 형태로 표현된다. 위 식에서 모수 τ2의 값이 곧 개별연구에서 나타나는 처리효과의 변동을 나타낸다. 고정효과모형 역시 변량효과모형의 한 경우라고 볼 수 있으며, 개별연구들 사이에 처리효과의 변동이 없을 경우 τ2값은 0이 되고 고정효과모형과 동일한 형태가 된다.
변량효과모형에서는 연구결과의 결합 시 개별연구의 변동과 연구들 간의 변동을 모두 고려한 가중치를 사용해야 한다. 따라서 메타분석을 이용하여 특정 대상의 처리효과를 결합하는 연구를 진행 할 때에는 개별연구들 간에 이질성이 존재하는지 파악하고, 이질성이 존재한다면 적절한 가중치를 계산 후 처리효과 모수 추정 시 사용해야 한다. 개별연구 간의 이질성을 통계적으로 확인하는 방법으로는 Cochran의 Q-검정14,15)과 Higgins의 I2-통계량16,17)을 많이 사용한다. 본 연구에서는 Q-검정을 개별연구의 통계적 이질성을 판정하는 기준으로 사용하고 I2-통계량은 보조지표로 제시하였다.
Q-검정은 H0:τ2=0을 귀무가설(본 연구에서는 ‘개별연구들 사이에 처리효과로 인한 변동이 없다.’로 설정)로 하여 다음과 같은 검정통계량을 사용한다.
연구들 사이의 변동 σ2이 알려져 있고 귀무가설(H0)이 옳다면, 검정통계량(Q)는 자유도 k-1인 χ2분포를 따를 것이다. 따라서 주어진 연구결과들로 메타분석을 실시할 때, 고정효과 모형과 변동효과모형 중 어느 것을 선택할 지에 대한 결정은 위의 검정통계량을 이용한 χ2검정을 통해 내릴 수 있다. 만약 통계적 검정 시 귀무가설(H0)이 기각된다면 개별연구들 사이에는 처리효과의 이질성이 존재한다고 보고 변량효과모형을 사용하여 개별연구들의 결과를 결합하여야 한다(실제 Q값을 계산할 때는 데이터로부터 추정치 를 구하여 사용한다).
변량효과모형에서 각 연구의 가중치를 계산하기 위해서는 먼저 처리효과 변동에 관한 추정치()를 계산하여야 한다. 를 계산할 때는 DerSimonian과 Laird가 제안한 방법18)을 널리 사용하고 있으며 이는 계산이 간편하고 모델의 이질성을 감소시키고 처리효과 추정 정확도를 높이는 변량을 포함하도록 확장할 수 있기 때문이다. DerSimonian과 Laird가 제안한 방법으로 τ2의 추정치, t를 구하면 아래와 같다.
여기서 q는 검정통계량이며, τ2은 처리효과가 가지는 분산이므로 값의 크기가 0보다 작을 수 없다. 따라서 처리효과 변동에 관한 추정치는() 다음과 같은 기준을 적용하여 선택한다.
위에서 구한 값을 사용하여 개별 연구에 대한 가중치를 아래와 같이 구할 수 있다.
결과적으로, 변량효과모형 중 가중최소제곱추정법(WLS)을 사용하여 처리효과에 대한 결합추정치(ORi)를 구하면 아래와 같다.
더불어 두 모형에 대한 95% 신뢰구간은 모두 아래와 같은 식으로 계산할 수 있으며,
변량효과모형의 경우 대신 값을 사용하여 계산한다.
2.4 보고편향
메타분석을 통한 연구결과들의 종합 시, 확인해야 할 중요한 요소 중 하나로 개별 연구들에 관해 보고(또는 출간)편향이 존재하는지 확인할 필요가 있다. 보고편향이란 통계적으로 유의한 결과를 나타낸 연구들만 보고(또는 출간)됨으로서, 해당 개별연구들만을 결합하여 결론을 도출 할 때 왜곡이 발생하는 것을 의미한다. 인위적으로 선택된 연구 결과들만 메타분석을 수행할 경우, 따라서 실제 효과보다 훨씬 더 긍정적인 결과를 제시하게 되어 부적절한 결론을 도출하게 된다.
보고편향의 존재여부를 확인하는 일반적인 방법으로 깔때기 그림(Funnel plot)을 활용한다. 깔때기 그림은 개별연구의 교차비를 가로축으로 하고, 표준오차를 세로축으로 그린 산점도의 하나로, 보고편향이 존재하지 않는 경우 깔대기를 뒤집어 놓은 것과 같은 형태로 그래프가 그려지게 된다.
만약 깔대기 그림의 특정 영역에서 개별 연구들의 결과값이 존재하지 않는 경우에는 보고편향이 존재하는 것으로 보고 결과해석 시 주의를 기울여야 한다. 본 연구의 경우, AEB의 장착효과가 유의성을 보인 특정 차량모델만 선택되어 결론이 도출될 경우 보고편향이 존재하는 것으로 간주될 수 있음에 따라 잘못된 결론 도출을 방지하기 위해 깔대기 그림을 활용하여 보고편향 존재여부를 확인하였다.
3. 데이터 및 분석결과
3.1 데이터 설정
본 연구에 사용된 데이터는 2014년~2017년 기간 동안의 보험개발원 자동차보험 기초통계자료로부터 추출하였다. 보험개발원은 자동차 보험업을 영위하는 국내 11개 손해보험사로부터 자동차보험 계약정보 및 사고자료를 집적하고 있다.
먼저 국내 5개 제작사에서 생산하는 차량모델 중 한 모델 내에서 AEB 장착이 기본으로 되어있는 트림과 장착 되어있지 않은 트림을 명확하게 구분할 수 있는 차량모델을 선택하였다. 정확한 AEB 장착의 사고경감효과를 추정하기 위하여 AEB 장착이 선택옵션으로 되어 있는 트림 또는 차종은 분석 대상에서 제외하였다. 다음으로 해당 기간 내 분석 대상 차량의 전체 운행대수를 추정하기 위하여 ‘평균 보유대수’의 개념을 사용하였다. 평균 보유대수는 선택한 차량모델 개별 트림의 전체 보험계약일수를 365일로 나눈 값으로, 개별 차종의 연간 운행대수를 추정할 수 있다. 사고 발생 비율 추정을 위한 사고 발생건수는 분석 대상 차량모델(트림) 사고 자료의 대물사고 발생건수를 사용하였다. 대물사고는 차대차 사고 발생 시 상대차 손해에 대해 보상한 사고를 말한다. 대물사고에 대한 자동차보험 가입은 국내에서 의무사항이므로 정확한 차대차 사고발생건수를 확인할 수 있다.
또한 ‘전체(All)’, ‘접촉(Minor)’, ‘추돌(Rear-end)’ 3가지 사고형태별 데이터를 각각 입수하여 분석하였다. 접촉사고와 추돌사고 발생건수는 전체사고에 포함되나, AEB의 작동 매커니즘을 고려할 때 사고 감소효과가 크게 나타날 사고유형임을 감안하여 별도로 분석하였다(차량 전・후면 충돌사고 중 사고심도가 크지 않은 사고를 접촉사고로 분류). 결론적으로 3가지 사고형태에 따른 AEB장치의 사고감소효과를 각각 분석한 후, 결과값이 도출되는 양상을 비교하고 가장 합리적인 AEB 장치 사고감소효과를 추정 하였다. 본 연구에 사용된 상세 데이터는 Table 1과 같다.
3.2 적용모델 타당성 검증
메타분석은 실험실에서 수행 불가능한 대규모의 처리・대조연구 결과 도출에 유용하다. 또한 확장성이 좋아 타 연구 또는 사후 연구와의 결합도 용이하다. 교통사고 데이터를 통한 연구가 후행적으로 진행되는 처리・대조연구의 하나임에 따라 향후 신규차량 출시 시 신규차량의 AEB 사고경감 효과를 기존차량과 결합하여 보다 정확한 AEB장치의 효과를 지속적으로 도출해야하는 점을 고려하여 본 연구의 분석 방법론으로 메타분석을 선정하였다.
한편 본 연구에서 분석방법으로 사용한 메타분석의 결과가 유의미한 지 확인할 수 있는 유의확률(p-value)의 값이 모형의 종류나 사고형태와 관계없이 0.05미만 수준으로 계산됨에 따라 메타분석을 통한 결과 해석의 타당성이 확인되었다. 아울러 ‘접촉(Minor)사고’에서 유의확률 값이 0.05를 일부 상회하나, 변량효과모형임을 고려할 때 전체 결론 도출에 적절할 것으로 판단된다.
3.3 분석결과
Table 2는 ‘전체’, ‘접촉’, ‘추돌’ 3가지 사고형태에 따른 AEB의 사고발생 감소효과를 메타분석으로 추정한 결과를 나타내고 있다. 먼저 사고형태에 관계없이 AEB 장착에 대한 ORi(교차비)는 모두 1보다 작게 나타났다. 이는 차량사고 발생비율을 확인해본 결과, 동일한 차량모델일지라도 AEB 장치가 장착된 차량들의 사고발생 비율이 10 % ~ 17 % 가량 작게 나타났다는 의미로 해석할 수 있다. 사고형태별로 나누어 보면, 전체사고에서 AEB 장치의 사고감소효과는 모델에 따라 11 % ~ 13 % 정도로 나타났고 접촉사고와 추돌사고는 각각 10 % ~ 11 %와 16 % ~ 17 %로 나타났다. 특히 추돌사고에서 AEB의 사고발생 감소효과 추정값이 가장 크게 나타난 것은 앞서 언급 했던 AEB의 작동 매커니즘이 전방 차량(또는 사람 등)을 인식하여 충돌방지를 위해 차량을 자동으로 제동시키는 시스템이기 때문에 추돌사고에서 장착효과가 가장 크게 나타날 것이라는 가정을 실제 사고 데이터를 통해 확인한 것으로 볼 수 있다.
Fig. 2는 각 차량모델의 ORi분포와 차량모델 사이의 AEB장착 효과 이질성 존재 여부 확인을 위한 숲 그림을 나타낸다. 숲 그림은 이질성의 존재 여부 및 정도를 시각적 방법으로 확인하는 대표적 방법으로서, ORi값 1.0을 기준으로 좌/우 영역에 연구들의 ORi와 95 % 신뢰구간을 표시하여 개별연구들의 처리효과 분포를 요약적으로 제시한다. Fig. 2에서 볼 수 있듯이 사고형태에 관계없이 9개 차량모델 중 6개 이상의 모델에서 AEB 장착효과에 대한 ORi가 1.0미만인 것으로 확인되었다. 차량모델 A2에서만 모든 사고형태에서 ORi가 1.0보다 크게 나타나고 교차비의 산포 또한 크게(특히 추돌사고 유형) 나타나도록 영향을 미쳤는데, 이는 A2차량의 경우 처리군(AEB 장착 모델)의 데이터수가 작고 대조군(AEB 미장착 모델)과의 데이터 비율도 큰 차이를 나타낸 것이 그 원인으로 추정된다. 따라서 A2 차량의 AEB 장착이 증가할 경우 사고유형별 사고경감 효과는 더욱 커질 것이라 사료된다. 아울러 A2 차량의 AEB 장치 성능에 대한 검증을 통해 타 모델과의 사고경감 효과 비교도 필요해 보인다(cf. 최대한 많은 AEB 장착 차량모델을 사용하여 종합적인 결론을 도출하기 위해 해당 데이터를 제거하지 않고 사용). 특히, 후면추돌(Rear-end) 사고유형의 ORi의 산포가 크고 낮은 값을 나타내는 모델이 존재하는 원인은 앞서 언급한 것처럼 AEB 장치의 본래 성능이 가장 잘 드러나는 추돌사고 유형에서 성능차이와 사고경감 효과가 사고통계를 통해 나타났기 때문으로 판단된다. 또한 Fig. 2에서 일부 차량모델의 ORi 신뢰구간이 겹치지 않고 있음을 알 수 있는데, 이는 제작사별, 동일 제작사라 할지라도 차량모델별로 AEB 장착효과가 다름을 보여주고 있다. AEB 장착효과 이질성 존재 여부는 Table 2의 Q값을 사용하여 보다 정확하게 평가할 수 있다. Table 2에서 볼 수 있듯이 전체사고에서 이질성 존재여부를 평가하기 위한 Q값은 44.60이었다. 유의수준 0.05 하에서 자유도 8인 χ2분포 값이 임을 고려할 때, 이는 귀무가설인 H0:τ2=0을 기각하며, 전체사고에서 제작사별, 차량모델별 AEB 장착효과가 다름을 추정할 수 있다. 이때 전체사고의 AEB 장착효과 변동에 관한 추정치는 = 0.0092 이었으며 I2=82.1%로 확인되었다. 접촉사고와 추돌사고에서도 유사한 결과가 도출되었다. Table 2에서 볼 수 있듯이 접촉사고와 추돌사고의 Q값은 각각 32.05, 109.68로서 모두 유의수준 0.05 하에서 귀무가설 H0:τ2=0 을 기각하고, AEB 장착효과의 이질성이 있음을 나타내었다. 이때 접촉사고의 AEB 장착효과 변동 추정치는 = 0.0714 이었고 I2=75.0%이었으며, 추돌사고의 변동 추정치는 = 0.0651, I2=92.7%로 가장 높게 나타났다. 차량모델에 따라 AEB 장착효과의 변동이 발생하는 원인은 차량 설계 차이로 인한 변동, AEB 설계 및 작동조건 차이로 인한 변동, AEB를 구현하는데 사용하는 레이더, 카메라모듈 등의 장비 차이로 인한 변동, 개별 차량모델의 운행 조건이나 해당 모델을 구매하는 구매자들의 차이(연령 또는 운전 습관 등)에 따른 변동 등이 있을 것으로 추정된다.
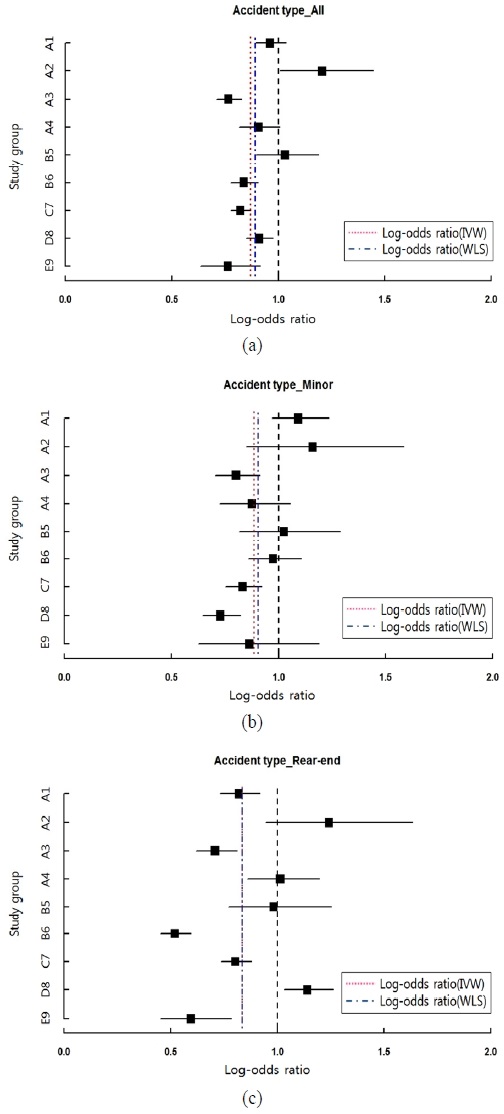
Forest graphs of estimated effects and confidence intervals for the 9 vehicle models using meta-analysis
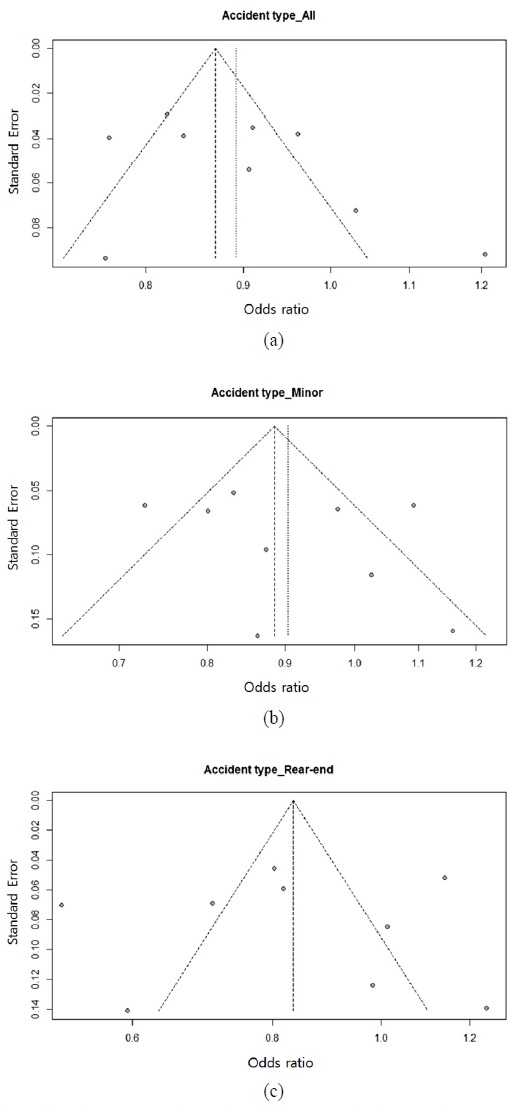
Fig. 3은 보고편향 존재 여부 확인을 위한 깔대기 그림을 나타낸다. 깔대기 그림을 통해 데이터의 오류 여부의 확인이 가능하며, 데이터의 오류가 없다면 좌우가 대칭인 모습을 보인다. Fig. 3과 개별연구의 수가 많지는 않지만, 전체’, ‘접촉’, ‘추돌’ 3가지 사고형태 모두에서 AEB 장치의 사고감소 효과 추정 교차비의 좌/우 모든 영역에 걸쳐 개별연구결과들이 분포하는 것을 확인할 수 있다. 더불어 개별연구의 분포가 임의적으로 나타남을 고려했을 때 차종선택으로 인한 편향이 존재한다고 볼 수 없다.
4. 결 론
AEB는 ADAS의 하나로 전방 차량 또는 보행자 등과 충돌을 방지하기 위한 시스템이다. 본 연구에서는 국내에서 운행 중인 9개 차량모델의 AEB 장착효과를 자동차보험 데이터에 메타분석 방법론을 적용하여 통계적으로 분석하였다.
보험개발원 자동차보험 사고데이터를 분석한 결과, 사고형태에 관계없이 AEB가 장착된 차량들의 사고발생 비율은 AEB가 장착되지 않은 차량에 비해 10 % 이상 낮게 나타났다. 전체사고의 경우 사고발생 비율이 약 11 % 낮았으며 접촉사고의 경우 약 10 %, 추돌사고의 경우 약 17 % 가량 낮게 나타났다. 이는 AEB 장착이 사고발생(특히 추돌사고) 감소에 효과가 있다는 것을 수치적으로 보여준다. 또한 AEB가 FCW, LDWS, LKAS, ACC 등 다른 ADAS 장비와 레이더, 카메라, 센서 등을 공유하며 차량에 함께 장착되어 있기 때문에, 차종에 따라서 ADAS 장비의 장착효과로 확장시켜 생각할 수도 있다. 또한 개별연구의 이질성평가결과는 제작사별, 차량모델별 AEB 장착 효과가 다르게 나타나는 것을 보여준다. 따라서 ADAS 설계 방향을 연구하거나 관련 정책을 수립할 때에 제작사 및 각 차량모델에 대한 심층적인 연구가 추가로 진행되어야 한다.
그동안 국내 자동차 관련업계에서 ADAS 장비의 장착효과를 추정하기 위해 사용하던 방법은 연구시설 실험으로부터 도출된 결과를 사용하여 추정하거나 해외발표사례를 인용하는 것이 대부분이었다. 본 연구는 따라서 그동안 실험적으로만 평가하던 국산 차량들의 AEB 장착 효과를 국내에서 발생한 실제 자동차사고 데이터를 이용하여 추정했다는 것에 그 의의가 있다. 운전자의 안전과 편의를 위한 ADAS 장비들은 앞으로 그 종류와 장착범위가 확대될 것이다. ADAS 장비들의 장착효과 분석은 자동차 제작업계뿐만 아니라 자동차보험 및 정비업계 등 자동차 산업 전반에 중요한 정보이므로 체계적인 데이터 집적과 과학적인 방법론을 적용한 분석을 지속적으로 추진할 예정이다.
Acknowledgments
본 연구는 보험개발원 2018년 사업계획인 “ADAS 성능 비교평가를 통한 사고율 경감 유도” 연구의 일환으로 수행되었습니다.
References
- J. B. Cicchino, Effectiveness of Volvo’s City Safety Low-Speed Autonomous Emergency Braking System in Reducing Police-Report Crash Rates, Insurance Institute for Highway Safety, (2016).
- J. W. Lee, N. K. Lim, and S. W. Shim, “A Study on Evaluation of Collision Avoidance Performance of AEB”, KSAE Annual Conference Proceedings, p944-945, (2014).
- J. W. Woo, M. G. Kim, and S. B. Lee, “Study on the Test Method of AEB and FCW System”, KSAE Spring Conference Proceedings, p1160-1163, (2013).
- K. Pearson, “Report on Certain Enteric Fever Noculation Statistics”, The British Medical Journal, 2(2288), p1243-1246, (1904).
-
G. V. Glass, “Primary, Secondary and Meta-analysis of Research”, Educational Researcher, 5(10), p3-8, (1976).
[https://doi.org/10.3102/0013189x005010003]

- A. L. Cochrane, Effectiveness and Efficiency: Random Reflections on Health Services, Royal Society of Medicine Press, London, Nuffield Provincial Hospitals Trust, (1972).
- A. L. Cochrane, 1931-1971: A Critical Review, with Particular Reference to the Medical Profession, Office of Health Economics, London, p1-11, (1979).
- H. S. Ahn, and H. J. Kim, “An Introduction to Systematic Review”, Journal of the Korean Medical Association, 57(1), p49-59, (2014).
-
R. Elvik, “Area-wide Urban Traffic Calming Schemes: A Meta-anylsis of Safety Effects”, Accident Analysis & Prevention, 33(3), p327-336, (2001).
[https://doi.org/10.1016/s0001-4575(00)00046-4]

- J. K. Caird, C. R. Willness, P. Steel, and C. Scialfa, “A Meta-analysis of Effect of Cell Phones on Driver Performance”, Accident Analysis and Prevention, 40(4), p1282-1293, (2008).
- IIHS, More Good News about Crash Avoidance: Volvo City Safety Reduces Crashes, Status Report, 48(3), (2013).
- S. E. Brockwell, and I. R. Gordon, “A Comparison of Statistical Methods for Meta-analysis”, Statistics in Medicine, 20(6), p825-840, (2001).
- J. Lee, “Meta-analysis”, Endocrinology and Metabolism, 23(6), p361-378, (2008).
- A. J. Sutton, K. R. Abrams, D. R. Jones, T. A. Sheldon, and F. Song, Methods for Meta-analysis in Medical Research, John Wiley and Sons, New York, (2000).
-
W. G. Cochran, “The Combination of Estimates from Different Experiments”, Biometrics, 10, p101-129, (1954).
[https://doi.org/10.2307/3001666]

-
J. P. T. Higgins, S. G. Thompson, J. Deeks, and D. G. Altman, “Statistical Heterogeneity in Systematic Reviews of Clinical Trials, a Critical Appraisal of Guidelines and Practice”, Journal of Health Services Research & Policy, 7(1), p51-61, (2002).
[https://doi.org/10.1258/1355819021927674]

-
J. P. T. Higgins, S. G. Thompson, J. Deeks, and D. G. Altman, “Measuring Inconsistency in Meta-analysis”, The British Medical Journal, 327, p557-560, (2003).
[https://doi.org/10.1136/bmj.327.7414.557]

-
R. DerSimonian, and N. M. Laird, “Meta-analysis in Clinical Trials”, Controlled Clinical Trials, 7(3), p177-188, (1986).
[https://doi.org/10.1016/0197-2456(86)90046-2]