Estimation of Tire Forces using Vehicle Linear Accelerations and Yaw Rate
Copyright Ⓒ 2019 KSAE / 167-01
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
This paper describes the estimation method of tire forces by using vehicle accelerations and yaw rate. The tire forces estimated here are front traction and front/rear lateral forces, which are essential for vehicle yaw dynamics. The proposed method are based on a well-known bicycle model of a front wheel drive vehicle. Therefore, this paper first reviews in detail a bicycle model for vehicle yaw dynamics focusing on linearization. Even with all of its simplicity and robustness, the bicycle model has errors in the yaw rate and aligning moment with the measurements, owing to the assumptions used for linearization. In particular, the estimation method using vehicle accelerations and yaw rate in this paper can predict the tire forces neglecting the complicated nonlinearity of the tire itself by installing an acceleration transducer in the vehicle. In order to assure its feasibility, several simulations have been performed and the results have been compared with the MF tire model and the cornering stiffness model. The performances in practice have been validated by comparing the experimental results of installing a tri-axial acceleration transducer and six-component wheel force transducers in the vehicle. Finally, the simulation and test results showed reliable performances for vehicle applications.
Keywords:
Tire forces, Vehicle linear acceleration, Yaw rate, Aligning moment, Bicycle model1. Introduction
Active safety systems such as ABS(anti-lock braking system) and ESC(electronic stability control) can significantly enhance the vehicle dynamic performances, and they are common in recent passenger cars. Such active safety systems use the vehicle dynamic equations described with vehicle states and external forces, which transmitted through tires. Based on these structural merits, vehicle motions can be stabilized by additional yaw moment generated as a result of the differences in driving or braking forces between the right and left sides of the tires, which is the so-called “Direct Yaw-moment Control” or “Torque Vectoring System.” In the direct yaw moment controller, the tire lateral forces directly affect dynamic performances of a vehicle. However for both technical and economic reasons, these dorminant variables are not measurable in a standard car. As a consequence, tire forces and side slip angle are not measured but observed or estimated by using various control theories and their practical modifications.
This paper focuses on the estimation of tire forces; there have been numerous numerical and experimental results such as using a road friction identification,1) a monitoring system,2) and a semi-physical tire model.3) Though the recent advances in the sensor technology, it is still difficult to measure the tire forces in real-time because of the nonlinearity of its dynamics, friction, and slippage on road, etc. However in our previous studies, the possibility of enhancement of the ESC performance has been numerically investigated by using wheel hub linear acceleration compared with the vehicle body acceleration.4) And we presented some experimental results of real-time estimation of tire lateral and vertical forces using wheel acclerations.5)
First this paper reviews a linearized bicycle model for vehicle yaw dynamic analysis in detail. The bicycle model is popular for predicting vehicle yaw motions because of its simplicity and robustness. However, there exist distinct errors of yaw rate and aligning moment with the measurements resulted from the assumptions used for linearization. In order to compensate these errors, many researchers have tried to develop mathematical models of the tire including its nonlinear characteristics like the MF tire model. But an estimation method presented here can predict the tire forces without complicate nonlinearity of tire itself by installing an acceleration transducer in the vehicle. To assure the feasibility of the proposed method, several simulations have been performed and compared the results with the MF tire model and the cornering stiffness model. Finally, its performances in practice have been validated by comparing with the experimental results installing a tri-axial accelerometer and six-component wheel force transducers in the vehicle.
2. Vehicle Yaw Dynamics
2.1 Review of a Linearized Bicycle Model
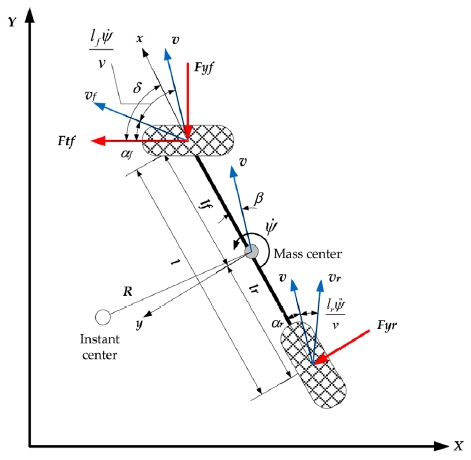
In order to predict the vehicle motion physically, it might be established a complicated nonlinear mathematical model. In analyzing the vehicle yaw dynamics, however a simplified bicycle model (1/2 car model) is widely used for its robustness and observability. Fig. 1 shows the free body diagram and kinematic variables in the bicycle model of a front wheel driven vehicle.6)
Preliminarily it does not consider the roll motion and longitudinal dynamics of a vehicle. Vehicle velocity at the mass center (v) acts in the direction tangential to the traveling curve and the lateral acceleration (aGy) toward the instant center of rotation. The vehicle side-slip angle (β) indicates the angle between the longitudinal axis of the vehicle body and the direction of velocity (v). And the vehicle body assumes to rotate around the mass center in a yaw rate ().
In the center of each axle, vehicle lateral or cornering forces (Fyf, Fyr) occur to balance with the centrifugal force exerted on the mass center. Each wheel rotates having slip angles (αf, αr) with respect to the center plane. In the direction perpendicular to the vehicle velocity, there is an instantaneous center of rotation consistent with the geometric center of the driving trajectory in steady-state cornering. From the free body diagram in Fig. 1, the yaw dynamic equations are obtained by relating the linear and angular accelerations of mass center (aGx, aGy, ) and the external forces (Ftf, Fyf, Fyr) exerted on the wheels as equation (1).
| (1) |
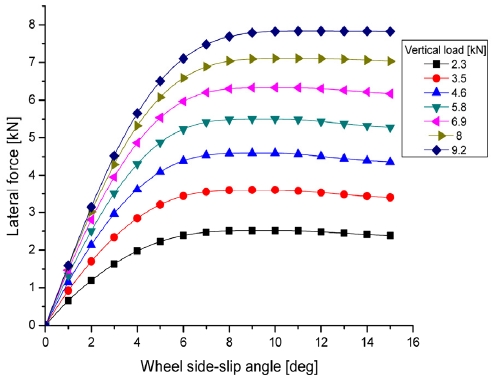
Tire lateral force varies with the frictional properties of the surface on which it is tested. Typically, the lateral force builds up as the tire slips sideways. Over the first few degrees, the buildup is linear with angle. This slope is called as the cornering stiffness and relates tire lateral forces with the wheel side-slip angle and tire vertical loads experimentally. Thus, the tire lateral forces can be linearized by using the tire cornering stiffness and wheel side-slip angle. As slip angle increases, the lateral force eventually peaks out at around 15 to 20 degrees of slip angle.7) Some studies have described observers which take cornering stiffness (or road friction) variations into account.1) Equation (2) shows how the front and rear tire lateral forces (Fyf, Fyr) relate with the equivalent tire cornering stiffness (Kf, Kr) and the side slip angles of front and rear wheel (αf, αr).8,9)
| (2) |
The bicycle model in equation (1) can be simplified into an equivalent 2-DOF model by neglecting tire tractive effort (Ftf) in the driving wheel and assuming the steering angle (δ) is relatively small for high speeds. The wheel side slip angles represent the angular direction of the linear wheel velocity relative to the longitudinal wheel axis; they are calculated by using the steering angle (δ), vehicle speed (v), yaw rate ( ), and vehicle side slip angle (β) as equation (3).
| (3) |
Let the vehicle side slip angle and yaw rate represent the system state variables. By defining the kinematic relationship as , and assuming local operating regime approximations, the numerical equations can be simplified into an equivalent linear 2-DOF model in equation (4).
| (4) |
2.2 Yaw Rate Errors owing to Linearization
The linearized bicycle model using the steering angle as an input is widely adopted in developing the yaw motion controller of a vehicle. However there exist inevitable errors with real vehicle behaviors because of the assumptions used for linearization. Thus, this subsection investigates the errors of the linearized bicycle model in detail.
In order to compare the yaw rate value calculated from equation (4) with the measurement, vehicle tests have been performed by a test car equipped with a yaw rate sensor. The test vehicle is an SUV (sports utility vehicle) which has the following specifications (see Table 1). And it is run on the dry-asphalt road; the tire cornering stiffness is shown in Fig. 2. The vehicle tests are a steady-state circular turn and a slalom maneuver. The detailed driving conditions are as follows:
- In the steady-state circular turning test, the vehicle turns to the right in 50 m radius and runs at 55 km/h; the steering angle is maintained as -90 degrees during the test.
- The steering angle changes in 0.2 Hz during a slalom test in a constant vehicle speed of 70 km/h.
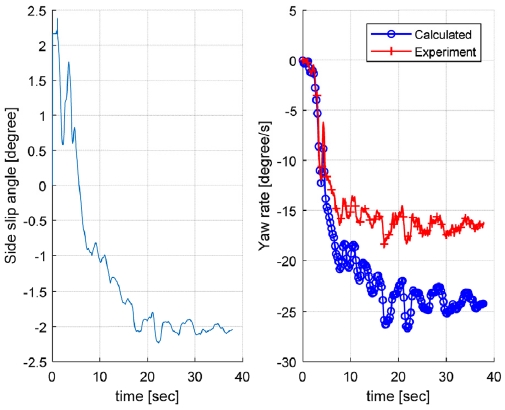
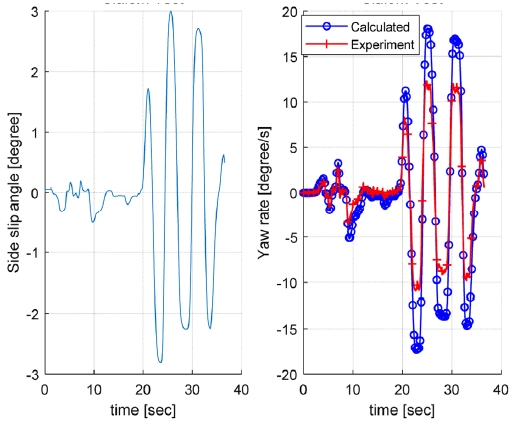
Fig. 3 and 4 show the computed side slip angle and compare the numerical and experimental values of the yaw rate in the vehicle tests. In these figures, though the yaw rate shapes of each result are quite alike, there exist a large difference between the numerical and experimental yaw rate values. In the circular turning test, the test vehicle has increased its speed to 55 km/h and turning radius up to 50 meters until 20 seconds. And this difference between the calculated and the real values increases until 20 seconds and is constantly maintained at about 8 degree/s thereafter(Fig. 3). Therefore this accumulated error has resulted from the steady-state assumption in the linearized bicycle model, although the test vehicle changes its speed.
The slalom test results are shown in Fig. 4. The vehicle speed has been increased up to 70 km/h for 20 seconds, and then the steering angle has changed repeatedly in 0.2 Hz maintaining the vehicle speed. Unlike the case of the circular turning test, the steady-state error of yaw rate does not appear but large differences whenever the steering angle changes.
From the comparison results, the linearized bicycle model in equation (4) predicts the vehicle yaw rate well in smooth and normal driving conditions: the lateral acceleration of vehicle is limited under about 4 m/s2.10) However, it is inevitable to have errors of yaw rate with the real values in rough and unsteady driving conditions because it assumes that the vehicle speed as constant and the lateral tire forces linearized with the tire cornering stiffness.
3. Estimation of Tire Forces using Vehicle Accelerations and Yaw Rate
In order to compensate the errors from the linearization of a bicycle model, several types of mathematical models of the tire have been developed. Different levels of accuracy and complexity are introduced in the various categories of utilization. In many articles dealt with vehicle dynamics, the tire forces are usually modeled as a function of slips between tire and road.8,9) Tire lateral force in the Magic Formula (MF) tire model, which is based on the work by Pacejka et al, varies with the frictional properties of the surface on which it is tested. It uses mathematical functions that relate the lateral force as a function of lateral slip, the longitudinal force as a function of longitudinal slip, and the aligning moment as a function of lateral slip.
This section describes another method of estimating the tire forces using the vehicle accelerations and the rate of yaw rate. The tire forces are re-formulated from the vehicle yaw dynamics using the bicycle model in equation (1). As the proposed method uses the vehicle states in backward, there is not necessary for the complicate experimental results of tire’s nonlinearity. Rearranging equations in (1), the tire forces making the vehicle yaw motion become as follows.
| (5) |
The tire forces directly affect the resultant aligning moment; it can be different from each other according to which tire force model used. Thus a couple of numerical simulations using CarSim software have been performed to assure the feasibility by comparing the vehicle aligning moment calculated by the proposed method with the linearized tire lateral forces using the cornering stiffiness in equation (2) and MF tire model. CarSim includes several tire models: a fully asymmetric table-based model, an extended model, the Pacejka 5.2 version of the magic formula, and MF Tire from TASS/TNO. The built-in models use nonlinear tables for lateral force, longitudinal force, aligning moment, and overturning moment as functions of slip, load, and camber.
The values of vehicle accelerations and yaw rate are obtained from the simulation results by the MF tire model of CarSim. The vehicle specifications used in the simulation are the same as Table 1. The simulations here are a steady-state circular turn and a double lane change maneuver. The detailed driving conditions are as follows:
- In a steady-state circular turn, the vehicle turns to the right in 50 m radius and runs at 60 km/h while the steering angle is maintained as 80 degrees.
- The steering angle changes in 1 Hz during a double lane change in a constant vehicle speed of 60 km/h.
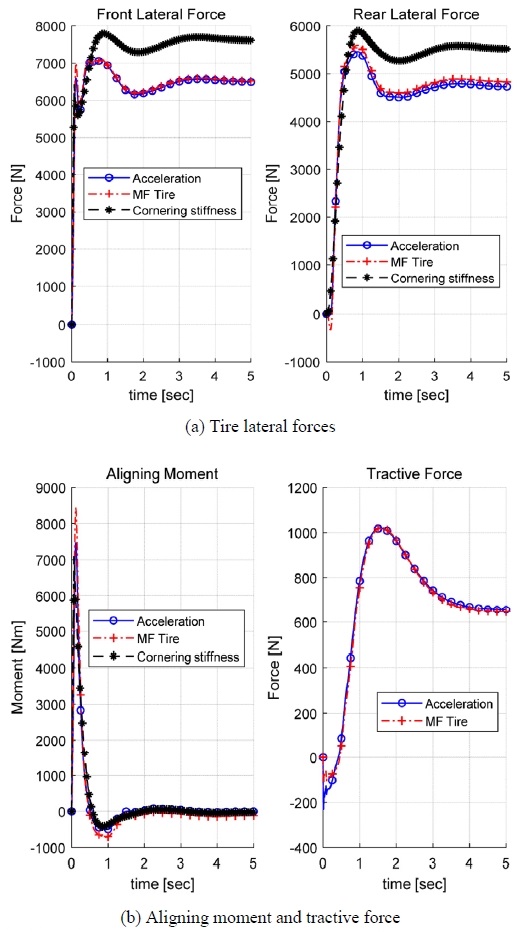
In the steady-state circular turn, the vehicle has reached the steady-state after 5 seconds (Fig. 5). The front and rear lateral forces have almost same values in both cases of using acceleration and MF tire model. However, the tire lateral forces calculated by using the cornering stiffness show a constant differences from other tire models in the steady-state (Fig. 5(a)). Since the cornering stiffness case does not take the tractive force into account, the front and rear lateral forces are larger than other cases. Especially the resultant aligning moment of MF tire case varies more sharply than other cases as soon as the vehicle moves (Fig. 5(b)).
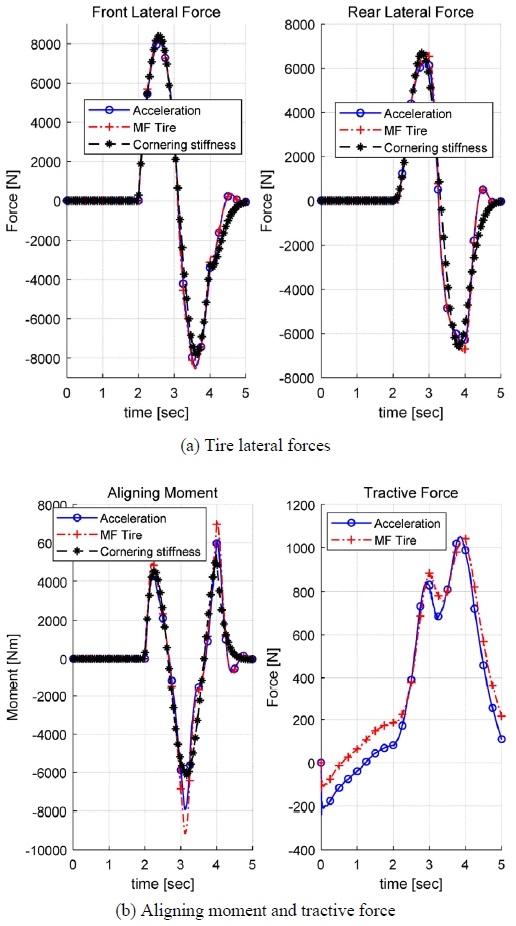
The magnitude of front and rear lateral forces in the double lane change maneuver show almost same values in all cases (Fig. 6(a)). Unlike the case of the circular turn, the cornering stiffness case does not show the steady-state errors but varies differently from other cases whenever the steering angle changes. Similar to the circular turn, the resultant aligning moment of MF tire case varies more sharply than other cases (Fig. 6(b)). Simulation results of the proposed method show consistent values with the MF tire model in magnitude and shape. From these figures, the cornering stiffness model cannot describes fully the dynamic behaviors of a vehicle in steering harshly.
4. Comparison of Experimental Results with Wheel Force Transducers
To estimate the tire forces in practice, it is necessary to install an acceleration transducer and yaw rate sensor in the vehicle body. Fortunately, most vehicles recently have the yaw rate sensor to supply the ESC function; the rate of yaw rate is differentiated directly from the ECU (Electronic Control Unit) signal. The raw acceleration signal from an accelerometer is so sensitive to a subtle movement that it is necessary to design the appropriate signal filter. Moreover, it should consider that the direction of accelerations of the vehicle varies with the changes of steering angles.4)
In order to verify the calculated values of tire lateral forces, the six-component wheel force transducers are also installed in each wheel. The transducer built in experiments can measure the acceleration in tri-axial directions (detailed specifications in Table 2). The vehicle specifications are the same to the aforementioned.
And two dynamic steering motions are imposed on the test vehicle. One is the single lane change and the other the slalom maneuver in a constant vehicle speed. The detailed driving conditions are as follows:
- In the single lane change test, steering angle is zero at start and varies within ±12 degrees; the steering angle changes in 1 Hz.
- The changes of steering angle are applied in 0.5 Hz during a slalom test in a constant vehicle speed and the vehicle speed is maintained as 75 km/h.
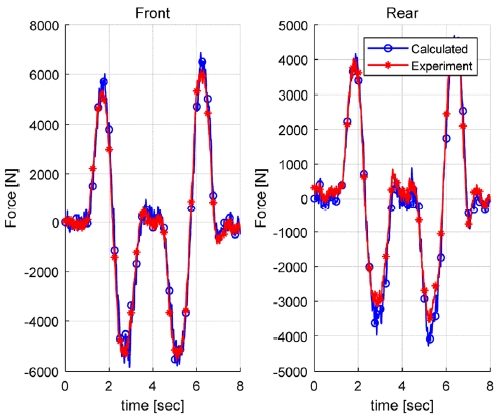
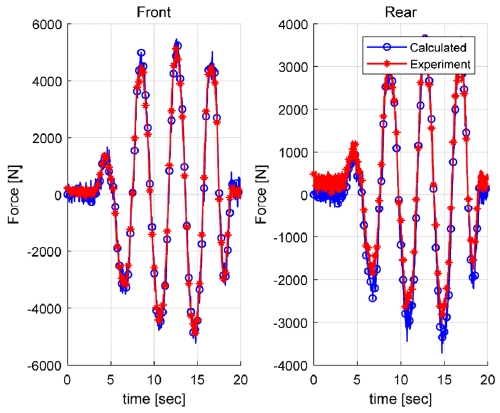
Fig. 7 and 8 depict the comparison of tire forces from the wheel force transducer and the calculated by using the accelerations and yaw rate. In those figures, the errors in the rear lateral forces are larger than in the front from the beginnings of the tests. Considering these errors are maintained consistently during the whole test period, it is supposed to be resulted from the incomplete calibration of the test equipment. Therefore the tire lateral forces calculated by using the accelerations and yaw rate accord with the experimental values well. Although it is expected that there exist time delays for differentiating the yaw rate and phase differences in accelerations between vehicle body and tire itself.
5. Conclusions
This paper describes the estimation method of tire forces using vehicle acceleration and yaw rate. The tire forces estimated here are front tractive and front/rear lateral forces, which essential for the vehicle yaw dynamics. And the proposed method are based on the well-known bicycle model of a front wheel driven vehicle. Despite of additional sensors in the vehicle body, simulation and test results show reliable performances of accuracy for vehicle applications. The conclusions are summarized as follows;
- 1) The bicycle model for vehicle yaw dynamics has been reviewed focusing on the linearization with the tire cornering stiffness. Though its simplicity and robustness, the linearized bicycle model reveals errors to predict vehicle yaw motions in changing speeds and steering harshly.
- 2) Based on the bicycle model, tire forces are re-formulated by using the vehicle accelerations and yaw rate. The proposed estimation method is not necessary for experimental results of tire’s nonlinearity unlike other numerical models of tire forces.
- 3) To assure the feasibility, a couple of CarSim simulations have been performed which compare the results of the cases of using cornering stiffness, MF tire model, and accelerations. The numerical results show that the proposed method can estimate the tire forces consistent with the MF tire model.
- 4) The performances in practice of the proposed method have been validated by comparing experimental results installing a tri-axial acceleration transducer and six-component wheel force transducers in the vehicle. The estimated tire lateral forces accords with the measured values in various dynamic yaw motions.
- 5) Although it is expected that there exist time delays for differentiating the yaw rate and phase differences in accelerations between vehicle body and tire itself. Estimation of tire forces using vehicle accelerations and yaw rate shows reliable performances for vehicle applications.
Nomenclature
| x : | longitudinal direction of a vehicle |
| y : | lateral direction of a vehicle |
| aG : | acceleration at a vehicle mass center |
| Ftf : | tractive force of a vehicle |
| Fyf : | front lateral tire force |
| Fyr : | rear lateral tire force |
| δ : | steering angle |
| lf, lr : | vehicle front and rear length |
| v : | vehicle linear velocity |
| : | yaw rate |
| β : | side-slip angle |
| af, ar : | wheel slip angles in front and rear |
| Iz : | mass moment of inertia with respect to yaw axis |
Acknowledgments
This work was supported by the sabbatical research grant from Daegu Catholic University in 2019.
References
- L. R. Ray, “Nonlinear Tire Force Estimation and Road Friction Identification: Simulation and Experiments”, Automatica, 33(10), p1819-1833, (1997).
-
K. Huh, J. Kim, and K. Yi, “Monitoring System Design for Estimating the Lateral Tyre Force”, Journal of Automobile Engineering, 217(Part D), p247-256, (2003).
[https://doi.org/10.1243/09544070360613219]

-
G. Gim, Y. Choi, and S. Kim, “A Semiphysical Tire Model for Vehicle Dynamics Analysis of Handling and Braking”, Vehicle System Dynamics, 43, p267-280, (2005).
[https://doi.org/10.1080/00423110500140849]

- H. Jo, J. Min, S. Lee, J. Park, and J. Kim, “Measurement Method of the Tire Lateral Force for the Use of Chassis Control System”, 10th International Symposium on Advanced Vehicle Control(AVEC), UK, (2010).
-
H. J. Yoon, and J. Kim, “Design of a Signal Transducer for Direct Conversion of Wheel Linear Accelerations into Tire Lateral Forces”, Int. J. Automotive Technology, 14(6), p897-902, (2013).
[https://doi.org/10.1007/s12239-013-0098-8]

-
P. Riekert, and T. E. Schunck, “Zur Fahrmechanik des gummibereiften Kraftfahrzeugs”, Ingenieur-Archiv, 11(3), p210-224, (1940).
[https://doi.org/10.1007/bf02086921]

- U. Kiencke, and L. Nielsen, Automotive Control System, Springer, Berlin, (2000).
-
C. Canudas-de-Wit, P. Tsiotras, E. Velenis, M. Basset, and G. Gissinger, “Dynamic Friction Models for Road/Tire Longitudinal Interaction”, International Journal of Vehicle Mechanics and Mobility, 39(3), p189-226, (2003).
[https://doi.org/10.1076/vesd.39.3.189.14152]

- H. B. Pacejka, and E. Bakker, “The Magic Formula Tyre Model”, Vehicle System Dynamics, 21(sup001), p1-18, (2007).
-
D. G. Tomas, Fundamentals of Vehicle Dynamics, Society of Automotive Engineers Inc., Warrendale, (1992).
[https://doi.org/10.4271/r-114]