SHPB와 Pulse Shaping Method를 이용한 CFRP의 압축 동적 물성에 관한 연구

1. 서 론

최근 항공우주, 자동차, 고속열차 등 운송수단의 구조설계 및 개발의 핵심 키워드는 경량화와 고강도이다. 운송수단의 연료 효율과 기계적 효율 향상을 위해 경량성과 고강도를 지닌 소재가 활발히 연구되고 있다. 기존의 경량화 및 고강도 소재로는 알루미늄 및 티타늄 합금 소재가 활발히 사용되었으나, 최근에는 적층 방향과 적층 각도 설계 등의 최적화를 통해 매우 가벼우면서도 강한 복합재료 소재가 각광받고 있다.^1-3)

복합재료는 두 가지 이상의 재료가 복합적으로 이루어져 원래의 소재보다 우수한 성능을 지니도록 한 재료를 의미하며, 일반적으로 재료의 이방성을 가지기 때문에 유연한 구조 및 재료 설계가 가능하다. 대표적인 예로는 시멘트와 CFRP(Carbon fiber reinforced plastic), Glass-epoxy 복합재료 등이 있다.¹⁾ 최근 고성능 및 연비 향상을 위해 보닛이나 범퍼, 프레임에 복합재료를 적용하고 있으며, 이러한 자동차 구성 요소의 충돌의 정확한 유한요소 해석을 수행하기 위해서는 동적 특성이 반영된 물성을 입력하여야 한다.⁴⁾

동적 물성을 획득하기 위한 방법은 변형률 속도마다 다르며, 그 중 SHPB(Split Hopkinson pressure bar) 실험은 소재의 변형률 속도 영역이 100~10000/sec일 때의 동적 물성을 획득할 수 있는 실험 기법이다.⁵⁾ SHPB 실험은 1차원 응력파 전달 이론 원리를 바탕으로 한다. 고강도 압력봉과 시편의 임피던스 차이에 의해 응력파의 반사와 투과가 이루어지게 되는데, 이 때 발생하는 투과 응력파와 반사 응력파의 관계식을 이용하여 시편의 동적 물성을 획득할 수 있다.

SHPB 실험은 시편이 일정한 변형률 속도를 갖고, 시편 내부의 응력이 평형하여야 한다는 가정을 필요로 한다. 이를 만족시키기 위해 Pulse shaping method가 제안되었으며, 응력파의 형태를 제어하여 일정한 변형률 속도와 동적 응력 평형에 기여할 수 있다.^6,7)

본 연구에서는 자동차 및 항공, 방위산업 분야에서 활발히 연구되고 있는 CFRP 소재의 압축형 동적 물성을 SHPB 실험 방법을 통해 획득하였다. 또한 Pulse shaping method를 적용하여 시편의 동적 평형도를 높이고, 변형률 속도를 일정하게 하여 물성 획득에 대한 신뢰도를 높일 수 있도록 하였다. 제작한 CFRP 시편은 상용 프리프레그를 적층하여 제작한 Woven 형태의 복합재료이며, In-plane 방향과 두께 방향에 대한 실험을 각각 수행하여 물성을 획득하였다.

2. SHPB 실험 개요

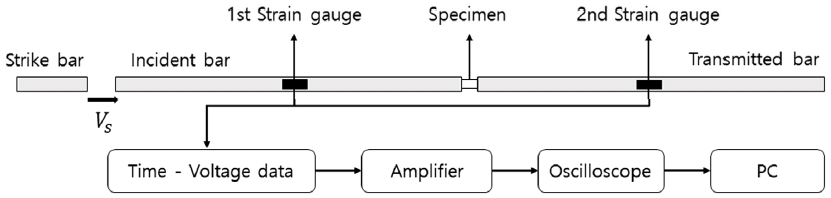
소재의 물성을 변화시키는 요인으로는 대표적으로 온도와 가공 경화, 변형률 속도가 있다. 변형률 속도가 고려된 물성 측정 방법은 변형률 속도 영역 별로 다르다.⁸⁾ 변형률 속도가 100/sec 이상일 때의 소재의 동적 물성을 획득하기 위해서 SHPB 실험이 널리 사용되고 있다. SHPB 실험은 Fig. 1과 같이 세 가지 압력봉으로 구성되며, 각각 충격봉(Strike bar), 입력봉(Incident bar), 그리고 출력봉(Transmitted bar)으로 명명한다. 충격봉에 일정 속도를 부과하면 충격봉과 입력봉이 충돌하고, 이에 따라 입사 응력파가 발생하게 된다. 충격에 의해 발생한 응력파는 입력봉의 축 방향으로 이동하며, 이와 동시에 입력봉의 압축 탄성 거동을 발생시키며 탄성 변형이 일어난다. 시편과의 경계에 도달했을 때 응력파의 일부는 반사되고 나머지는 투과한다. 투과파와 반사파에 의해 발생하는 변형률을 스트레인 게이지를 이용하여 측정하고, 데이터 획득 시스템을 이용하여 시편의 물성에 의한 식으로 변환할 수 있다.

Fig. 1

Schematic diagram of SHPB experiments

2.1 SHPB 이론식

SHPB 실험에서 시편의 전면 및 후면에 대한 응력은 식 (1)과 식 (2)와 같이 나타낼 수 있다.

$\[ {\sigma }_1=E_B\frac{A_B}{A_s}\left({\epsilon }_I+{\epsilon }_R\right) \]$

(1)

$\[ {\sigma }_2=E_B\frac{A_B}{A_s}\left({\epsilon }_T\right) \]$

(2)

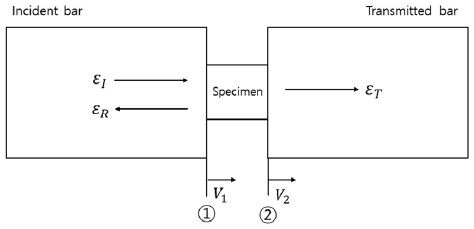
식 (1)은 시편의 전면과 입력봉의 경계면(Fig. 2의 ①)에서 발생하는 응력의 크기이며, 식 (2)는 시편의 후면과 출력봉의 경계면(Fig. 2의 ②)에서 발생하는 응력의 크기이다. 동적 응력 평형이 이루어졌다는 것은 위의 두 식이 동일하다는 의미이며, 두 식이 같다고 가정하면 다음과 같이 나타낼 수 있다.

Fig. 2

Testing section of SHPB experiments

$\[ {\epsilon }_T={\epsilon }_I+{\epsilon }_R \]$

(3)

시편 내부에서 이상적으로 동적 평형이 이루어진 경우, 입사파와 반사파에 의한 탄성 변형률의 합은 투과파에 의한 탄성 변형률과 같다. 식 (3)을 가정하여 시편의 공칭 변형률 속도와 이를 적분한 공칭 변형률, 그리고 시편의 평균 공칭응력을 도출할 수 있다. 시편의 평균 변형률 속도와 평균 공칭 변형률, 평균 공칭 응력을 식 (4)와 (5), (6)에 나타내었다.

$\[ \dot{\overline{e_s}}=-\frac{2C_0}{L_s}{\epsilon }_T \]$

(4)

$\[ \overline{e_s}=-\frac{2C_0}{L_s}{\int }_0^t{\epsilon }_{T}dt \]$

(5)

$\[ \overline{{\sigma }_s}=E_B\frac{A_B}{A_s}{\epsilon }_T \]$

(6)

2.2 SHPB 실험 장비 구성

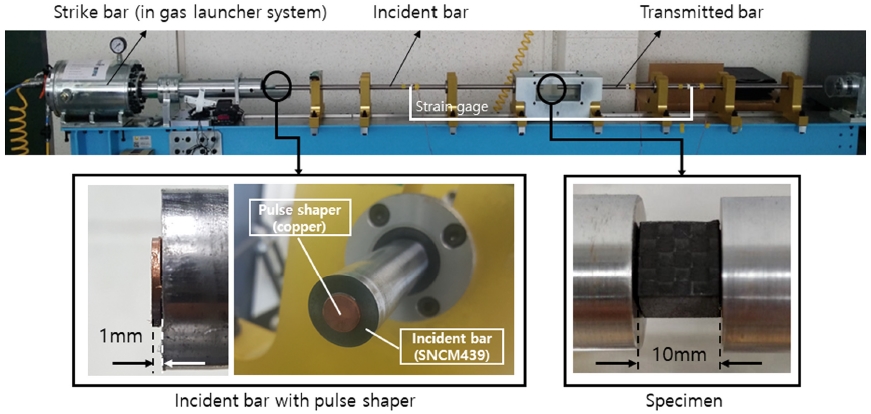
동적 물성 획득을 위한 SHPB 실험 장비의 모습은 Photo. 1과 같다. 실험 장비는 충격봉에 속도를 가하기 위한 공압 발사 장비와 세 압력봉, 축 가이드, 스토퍼, 데이터 획득 시스템으로 구성하였다.

Photo. 1

SHPB experiments apparatus in Pusan national university

2.2.1 압력봉

세 압력봉은 탄성 영역 내에서 거동하여야 하기 때문에 강도가 매우 높아야 한다. 또한 압력봉 끝단에서 응력파의 손실 등이 발생할 수 있다. 이를 위해 열처리 공정으로 강도를 높였으며, 정밀 연삭 공정을 통해 응력파의 손실을 최소화하였다. 압력봉의 물성은 Table 1과 같다.

Table 1

Material properties of pressure bars

2.2.2 공압 발사장비

공압 발사 장비를 사용한 이유는 충격봉의 속도 제어가 용이하여 일정한 충격봉의 속도를 도출할 수 있다. 이에 따라 실험의 재현성을 확보하여 시편의 변형률 속도를 일정하게 할 수 있다.

2.2.3 축 방향 가이드 및 스토퍼

응력파의 원활한 1차원 전달을 위해서는 세 압력봉의 축이 일치하여야 한다. 축 방향 가이드는 세 압력봉의 축이 일치할 수 있도록 한다.

스토퍼는 출력봉 후방에 부착되어 있다. 충격에 의해 발생한 압력봉의 운동에너지를 감쇠시키고, 압력봉이 축 방향 가이드를 빠져나가는 것을 방지한다.

2.2.4 데이터 획득 시스템

데이터 획득 시스템은 응력파에 의해 발생하는 변형률을 측정하기 위한 스트레인 게이지와 휘트스톤 브리지, 신호 증폭기 및 오실로스코프로 구성된다. 응력파에 의해 변형이 발생하면 스트레인 게이지에서 저항 변화가 발생하며, 휘트스톤 브리지 케이블에서 저항 변화에 따른 전압을 감지한다. 증폭기를 이용하여 전압 데이터 신호를 증폭시킨 후, 고해상도 오실로스코프를 이용하여 시간에 따른 전압 데이터를 측정할 수 있다. 본 연구에서 사용된 휘트스톤 브리지 회로는 쿼터 브리지 시스템으로, 응력 측정 시 많이 사용되는 시스템이다.

이외에도 충격봉의 속도를 측정할 수 있는 포토 게이트 시스템이 있다.

3. CFRP의 압축 동적 물성

“복합재료는 두 가지 이상의 재료가 조합되어 물리적·화학적으로 서로 다른 상을 형성하면서 보다 유효한 기능을 발현하는 재료를 말한다. 강화재의 구조에 따라, 강화되는 기지재료의 종류에 따라 나누어진다.”¹⁴⁾ 수많은 종류의 복합재료 중, CFRP는 카본 소재의 섬유가 강화 플라스틱 기지로 구성된 복합재료이다. CFRP 소재는 비강도와 비강성이 높아 자동차 및 항공 산업에서 많은 연구가 진행되고 있다.

3.1 CFRP 시편 제작 및 가공

SHPB 실험을 수행하기 위해 CFRP 시편을 제작하였다. 일반적인 SHPB 실험에서는 원기둥 형상의 시편을 사용한다. 시편의 형상을 원기둥으로 제작하는 이유는 시편 반경 방향으로 응력파의 분산을 최소화하여 축 방향으로의 1차원 응력 전달을 원활하게 하기 위함이다. 참고문헌에 따르면 시편의 단면 형상에 따라 미소한 변화는 발생하지만 응력파의 전달과 응력파의 형태에 큰 영향을 주지 않는다.¹²⁾ 따라서 본 연구에서는 가공비 및 제작비를 절감하기 위해 Photo. 2와 같이 시편을 정육면체 형상으로 가공하였다.

Photo. 2

CFRP specimen used in SHPB experiments

방향성을 가진 CFRP 소재의 방향에 따른 물성을 획득하기 위해서는 실험하고자 할 방향으로 적층판을 별도로 제작하여야 한다. 그러나 정육면체로 시편을 제작할 경우, 시편을 간단히 회전하여 In-plane 방향과 두께 방향 모두 실험할 수 있다는 장점이 있다.

정육면체 CFRP 시편 제작 과정은 다음과 같다. 수지와 탄소섬유를 일정 비율로 혼합한 판재 형태의 탄소섬유 강화소재인 프리프레그를 총 50장 적층하여 두께 10 mm인 적층판을 제작하였다. 적층에 사용된 프리프레그는 SK chemicals 社의 WSN3KY이며, 물성은 Table 2와 같다.¹³⁾ 제작된 적층판은 워터 젯을 이용하여 정육면체 형상으로 가공하였다.

Table 2

Material properties of WSN3KY prepreg (3K fabric 50 ply)

3.2 SHPB 실험 조건 및 결과

Photo. 3과 같이 실험 장비를 구성하여 In-plane 방향과 두께 방향에 대해 CFRP 소재의 동적 물성을 획득하였다. Pulse shaper를 부착하여 실험을 수행하였고, 시편을 압력봉에 부착시키기 위해 점성을 가진 바세린을 이용하였다. CFRP 소재의 변형률 속도에 따른 동적 압축 물성을 획득하기 위해 공압 발사장비의 압력을 0.5 bar 간격으로 부과하여 실험을 수행하였다.

Photo. 3

Configuration of SHPB experiments with pulse shaper and CFRP specimen

3.2.1 In-plane 방향으로의 압축 동적 물성

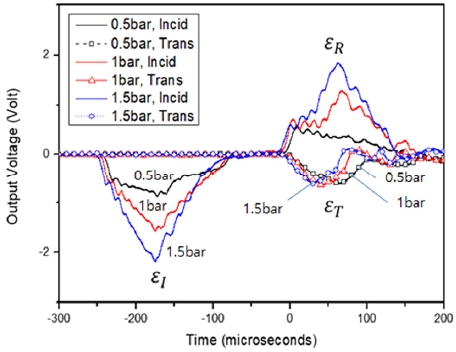
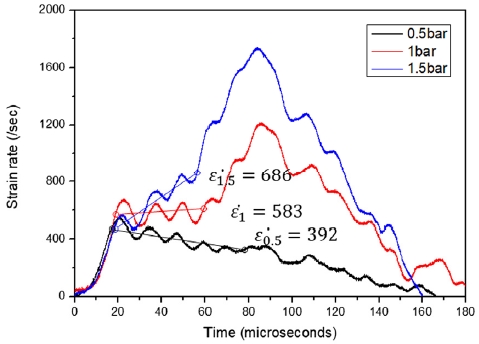
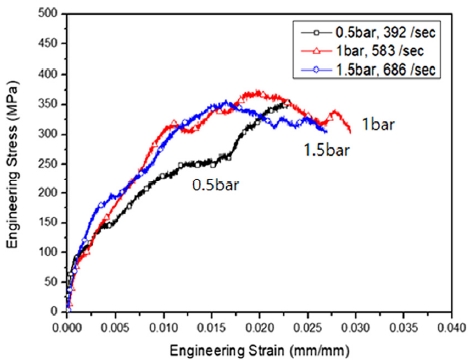
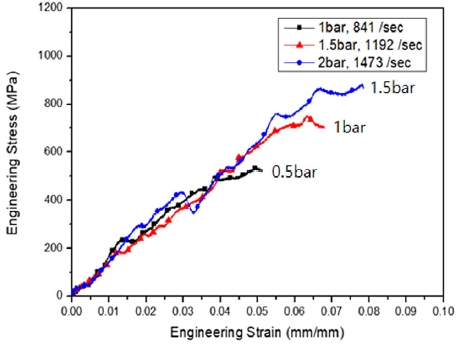
In-plane 방향(섬유 방향이 응력파 전달 방향과 일치)으로 시편을 부착한 후 실험하여 얻은 시간-전압 그래프를 Fig. 3에 나타내었다. 인가 압력에 따라 변형률 속도가 명확히 달라지는 것을 반사파를 통해 확인하였으며, 이를 통해 변형률 속도 이력을 Fig. 4와 같이 나타내었다. Fig. 4의 인가 압력 별 변형률 속도 값은 변형률 속도가 일정한 구간(첫 번째 원과 두 번째 원까지의 구간)의 중간값을 사용하였으며, 변형률 속도가 일정하게 유지되다가 급격히 증가하는 구간을 시편의 파단점으로 예측하였다. 이는 파단에 의해 응력파의 투과가 발생하지 않기 때문에 응력파가 전달되지 못하고 모두 반사되기 때문에 발생하는 현상으로 예측하였다. Fig. 5의 응력-변형률 선도는 최대 응력이 발생하는 변형률(0.5 bar, 392/sec)과 파단점으로 예측되는 변형률(1 bar, 583/sec 및 1.5 bar, 686/sec)까지 그래프를 작성하였다. 0.5 bar의 인가 압력을 부여하였을 때에는 Photo. 4의 (a)와 같이 완전 파단이 발생하지 않았기 때문에 변형률 속도 이력에서 파단점을 예측하기 어려워 최대 응력 발생지점까지 선도를 작성하였다. 반면, 1 bar 이상을 입력하였을 때에는 Photo. 4의 (b)와 같이 완전 파단이 발생하였고, 변형률 속도 이력에서 시편의 파단 예측 지점을 찾기가 용이하였기 때문에 파단 지점까지 선도를 작성하였다.

Fig. 3

Time-voltage data of CFRP in-plane direction

Fig. 4

Strain rate history about in-plane direction

Fig. 5

Stress-strain curve of CFRP in-plane direction

Photo. 4

CFRP specimen used in SHPB experiments

Table 3

Material properties of WSN3KY prepreg (3K fabric 50 ply)

Fig. 5에서 변형률 속도에 따른 강성 저하가 발생한 이유는 일반적인 정적 압축시험과 달리, 응력파에 의해 시편의 파단이 지속적으로 축적되면서 발생하는 현상으로 분석하였다.

In-plane 방향의 경우, 파단 여부에 따라(0.5 bar, 1 bar) 변형률 속도 민감도와 강도, 그리고 강성의 차이가 나는 것을 확인하였다. 또한, 완전 파단이 발생하였을 때(1 bar, 1.5 bar) 변형률 속도가 증가하면 파단 변형률은 감소하는 것을 확인할 수 있다.

3.2.2 두께 방향으로의 압축 동적 물성

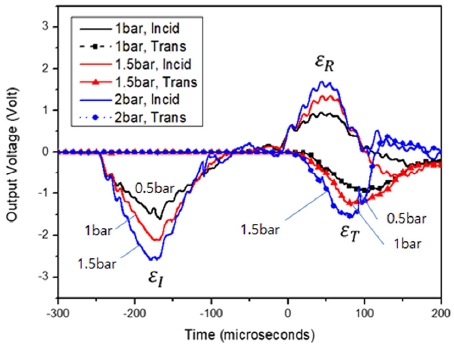
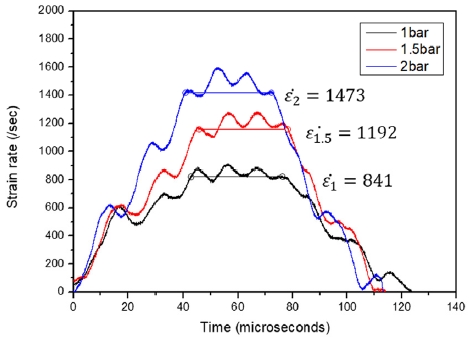
두께 방향(적층 방향이 응력파 전달 방향과 일치)으로 시편을 부착한 후 실험하여 얻은 시간-전압 그래프를 Fig. 6에 나타내었다. In-plane 방향과 마찬가지로 인가 압력을 증가시킴에 따라 변형률 속도가 증가하는 것을 확인할 수 있다. Fig. 7과 같이 두께 방향으로의 변형률 속도 이력에서도 인가 압력 크기와 변형률 속도는 비례하는 경향을 나타내었다. 그러나 변형률 속도 이력에서의 경향이 In-plane 방향과는 다른 것을 확인할 수 있다. 두께 방향으로 실험하였을 때에는 2 bar 이상의 인가 압력에서도 시편의 완전 파단이 발생하지 않았기 때문에(Photo. 4의 (c)) 변형률 속도가 일정한 구간 이후 변형률 속도가 급격히 증가하는 구간을 찾을 수 없다.

Fig. 6

Time-voltage data of CFRP thickness direction

Fig. 7

Strain rate history about thickness direction

Fig. 8의 응력-변형률 선도는 최대 응력이 발생하는 변형률까지 그래프를 작성하였다. 변형률 속도에 따라 강성의 차이는 없으나, 최대 응력이 도출되는 변형률이 달라지는 것을 확인할 수 있다. Fig. 8에서 변형률 속도에 따른 강성의 변화가 없는 이유는 시편 내부의 파단 축적이 발생하지 않았기 때문이라고 판단하였다.

Fig. 8

Stress-strain curve of CFRP thickness direction

3.2.3 실험 후 시편 파괴 형상

Photo. 4의 In-plane 방향 (a)와 (b)에서 볼 수 있듯이, 실험 후 시편의 파단 경향은 층간 박리(Delamination, 적층된 복합재 층이 분리되는 현상)가 발생하였다. 또한, 완전 파단이 발생한 (b)의 경우에는 횡방향 전단 파단(Lateral shear, 적층 축의 수직한 방향으로 발생한 전단 현상), 쪼개짐(Splitting, 프리프레그가 섬유방향 결을 따라 여러 개로 나누어지는 현상), 브루밍(Brooming, 끝단이 빗자루처럼 벌어지는 현상) 등이 추가적으로 나타난 것을 확인하였다. 두께 방향에서는 Photo. 4의 (c)와 같이 층간 박리는 일어나지 않았으며, 종방향 전단 파단(Transverse shear, 적층 두께 방향으로 발생한 전단 현상)과 두께 방향 쪼개짐 현상이 복합적으로 발생한 것을 확인하였다.

3.2.4 CFRP 압축 동적 물성의 곡선 접합

CFRP의 In-plane 방향과 두께 방향의 동적 물성 그래프를 이용하여 곡선 접합을 수행하였다. 곡선 접합에 사용된 수식은 다음과 같다.

$\[ \sigma =\alpha e^{\beta } \]$

(7)

일반적인 복합재료의 유동 응력은 선형을 나타낸다. 그러나 원본 데이터의 비선형 특성을 고려하여 식 (7)과 같이 멱함수 형태로 나타내었으며, 결과는 Fig. 9와 같다. 곡선 접합에 사용된 매개 변수를 Table 4에 정리하였다.

Fig. 9

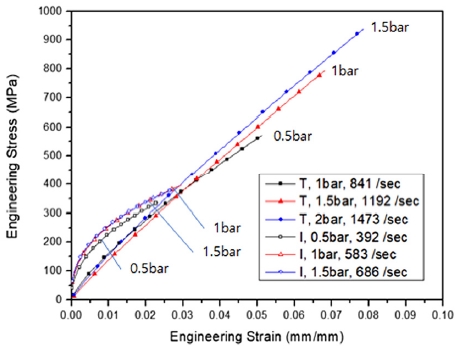
Curve fitting about dynamic material properties of CFRP laminate (T : thickness direction, I : in-plane direction)

Table 4

Parameters of power function

곡선 접합을 통해 예측한 멱함수와 실험에서 얻은 물성의 일치도를 평가하기 위해 결정계수(R) 값을 도출하였다.

$\[ R^2=1-\frac{RSS}{TSS} \]$

(8)

$\[ TSS=\sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2 \]$

(9)

$\[ RSS=\sum _{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2 \]$

(10)

식 (8)은 결정계수를 나타내는 식으로, 값이 1에 가까울수록 두 데이터 집단의 일치도가 높다는 것을 의미한다. 결정계수 값을 계산하기 위해 식 (9)와 (10)이 사용된다. 식 (9)는 Total sum squares로써, 실제값과 중간값 차의 제곱 합을 의미한다. 식 (10)은 Residual sum of squares로, 실제값과 예측값에서 발생하는 잔차의 합을 의미한다. RSS 값이 작을수록 실제값과 예측값의 적합도가 높다.

In-plane 방향 및 두께 방향으로의 모든 물성에 대해 결정계수 값을 비교한 결과, 0.9 이상의 값을 나타내었다. 따라서 곡선 접합 회귀모델의 일치도는 높다고 할 수 있다.

4. 결 론

본 연구에서는 SHPB 실험 기법과 Pulse shaping method를 이용하여 두 방향에 대해 CFRP 소재의 압축 동적 물성을 획득하였고, 파단 경향 및 특성을 분석하였다. 이에 대한 결론은 다음과 같다.

• 1) In-plane 방향의 동적 압축 강도보다 두께 방향의 동적 압축 강도가 높다.
• 2) In-plane 방향의 압축 강도는 완전 파단이 발생하였을 때 변형률 속도에 큰 영향을 받지 않으나, 변형률 속도가 증가하면 파단 변형률은 감소한다.
• 3) In-plane 방향과 두께 방향으로의 변형률 속도에 의한 강성의 변화는 크지 않다.
• 4) In-plane 방향의 파단 경향은 다양하고 완전한 파단이 발생하나, 두께 방향의 파단 경향은 단순하고 완전한 파단이 발생하지 않았다.
• 5) 향후, 획득한 동적 물성을 통해 복합재료 파손 모델(Damage model)의 매개변수를 확보한 후 실험과 해석을 비교하여 획득한 물성의 정확성을 검증하여야 할 것이다.

Acknowledgments

이 논문은 2015년도 정부(미래창조과학부)의 재원으로 한국연구재단의 선도연구센터지원사업(No. 2012R1A5A1048294)과 2017년도 정부(미래창조과학부)의 재원으로 한국연구재단의 이공학개인기초연구지원사업(No. NRF-2017R1D1A3B03034265)의 지원을 받아 수행된 연구임. 이에 관계자 여러분께 감사드립니다.

References

• R. M. Jones, Mechanics of Composite Materials, 2nd Edn., CRC Press, Philadelphia, (2014).
• T. Gao, and J. U. Cho, “A Study on Damage and Penetration Behaviour of Carbon Fiber Reinforced Plastic Sandwich at Various Impacts”, International Journal of Precision Engineering and Manufacturing, 16(8), p1845-1850, (2015). [https://doi.org/10.1007/s12541-015-0240-9]
• J. Harding, “Effect of Strain Rate and Specimen Geometry on the Compressive Strength of Woven Glass-reinforced Epoxy Laminates”, Composites, 24(4), p323-332, (1993). [https://doi.org/10.1016/0010-4361(93)90042-7]
• B. E. Lee, D. S. Kang, E. T. Park, J. Kim, B. S. Kang, and W. J. Song, “Numerical and Experimental Investigation on Impact Performance of Fiber Metal Laminates Based on Thermoplastic Composites”, Transactions of KASE, 24(5), p566-574, (2016). [https://doi.org/10.7467/ksae.2016.24.5.566]
• G. T. Gray, Classic Split-Hopkinson Pressure Bar Technique, ASM International, Mechanical Testing and Evaluation, ASM Handbook, 8(3), (2000).
• W. W. Chen, and B. Song, Split Hopkinson (Kolsky) Bar: Design, Testing and Applications, Springer Science & Business Media, New York, (2010).
• O. S. Lee, and D. H. Kim, “Reliability Estimation and Dynamic Deformation of Polymeric Material Using SHPB Technique and Probability Theory”, Transactions of the Korean Society of Mechanical Engineers A, 32(9), p740-753, (2008). [https://doi.org/10.3795/ksme-a.2008.32.9.740]
• S. Nemat-Nasser, Introduction to High Strain Rate, ASM International, Mechanical Testing and Evaluation, ASM Handbook, 8(3), (2000).
• P. Baranowski, J. Malachowski, R. Gieleta, K. Damaziak, L. Mazurkeiewicz, and D. Kolodziejczyk, “Numerical Study for Determination of Pulse Shaping Design Variables in SHPB Apparatus”, Bulletin of the Polish Academy of Sciences Technical Sciences, 61(2), (2013). [https://doi.org/10.2478/bpasts-2013-0045]
• S. Ellwood, L. J. Griffiths, and D. J. Parry, “Materials Testing at High Constant Strain Rates”, Journal of Physics E: Scientific Instruments, 15(3), p280, (1982). [https://doi.org/10.1088/0022-3735/15/3/009]
• Y. H. Kim, M. A. Woo, B. S. Kang, and J. Kim, “Numerical and Experimental Verification of Stress Wave Control Effect in SHPB Experiment using Pulse Shaper”, Transactions of Materials Processing, 26(5), p314-322, (2017). [https://doi.org/10.5228/kstp.2017.26.5.314]
• O. Sen, S. A. Tekalur, and P. Maity, “On the Use of Non-cylinderical Specimens in a Split-Hopkinson Pressure Bar”, The Journal of Strain Analysis for Engineering Design, 46(8), p866-878, (2011). [https://doi.org/10.1177/0309324711410127]
• SK Chemicals, Physical Properties Cured Laminate Properties (USN and WSN grade), http://www.skchemicals.com/business/sf_pop.do?no=2 (2019).
• Doopedia, Composite Materials, http://www.doopedia.co.kr/doopedia/master/master.do?_method=view&MAS_IDX=101013000844619 (2019).