횡방향 안정성 향상을 위한 샤시통합제어 개발
Copyright Ⓒ 2019 KSAE / 165-05
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
This paper describes an integrated chassis control(ICC) for improving lateral vehicle stability through the control system integration of the active front steering(AFS), rear wheel steering(RWS), and electronic stability control(ESC). The proposed ICC logic consists of the integrated vehicle observer(IVO) to estimate vehicle states, integrated target generator(ITG), integrated vehicle controller(IVC), and optimal distribution controller(ODC). The ITG determines a target motion of a vehicle based on the IVO. In order to achieve the target motion, the IVC calculates the target yaw moment and target lateral force. The target yaw moment and target lateral force can be generated in coordination with the AFS, RWS, and ESC system via the ODC. Vehicle tests were conducted in order to investigate the performance of the proposed control system on dry asphalt road. The experimental result shows that the ICC logic effectively maintains lateral vehicle stability.
Keywords:
ICC, Active front steering, Rear wheel steering, Electronic stability control, Lateral stability, Optimal distribution, Sideslip angle키워드:
샤시통합제어, 전륜능동조향시스템, 후륜능동조향시스템, 안정성제어시스템, 횡안정성, 최적분배, 횡슬립각1. 서 론
최근 고성능 차량에 대한 수요, 특히 차량의 핸들링 성능 개선에 대한 소비자들의 요구가 높아지고 있다. 차량의 핸들링 성능은 샤시, 차체, 및 구동계의 특성이 복합적으로 반영되어 결정되며, 승차감과 같은 타 성능과 Trade-off 관계에 있기도 하다. 따라서 핸들링 성능 육성 시 타 성능과의 조화로운 균형을 반드시 고려해야 한다. 이러한 차량의 핸들링 성능을 개선하기 위해 많은 엔지니어들이 샤시통합제어에 대한 연구를 수행해왔다.1-4) 본 연구에서는 차량 자세를 제어하는 대표 시스템인 ESC와 능동 조향시스템인 AFS와 RWS를 통합하여 차량의 횡방향 거동을 안정화시키는 샤시통합제어에 대한 연구를 수행하였다. 특히 Top-down 방식의 제어 흐름을 기반으로 상위에서 설계된 제어 모멘트 및 제어 힘을 개별 액추에이터의 성능 제약을 고려한 실시간 최적화과정을 거쳐 개별 시스템 제어량으로 분배하는 것을 그 특징으로 한다.
AFS와 RWS는 능동 전/후륜 조향시스템으로 차량의 전/후 조향각을 능동적으로 조절하여 차량의 민첩성과 안정성을 확보해 주며 ESC는 각 휠의 독립 제동을 통해 차량의 안정성을 확보해주는 시스템이다. 이 세 시스템들은 서로 다른 시스템이지만 차량 관점에서는 차량의 요 모멘트를 발생 시킨다는 공통점이 있고, AFS와 RWS은 차량의 횡력을 추가로 발생시킬 수 있다. 이러한 시스템 특성을 활용하여 본 연구에서는 차량 목표 거동 선정, 상위 거동 제어기 설계, 액추에이터 한계를 고려한 최적 분배 과정을 통한 차량의 횡안정성 개선에 대한 연구를 수행하였다.
본 논문에서 제안한 샤시통합제어 로직은 IVO, ITG, IVC 그리고 ODC 이렇게 4 가지 세부 모듈로 구성되어 있다. IVO에서는 측정이 어려운 차량 상태 변수인 각 바퀴 타이어 하중, 종/횡 방향 타이어 힘, 횡 방향 슬립각, 슬립률 그리고 노면 마찰계수 등을 추정한다. ITG에서는 차량의 현재 상태에서 추종해야 할 목표 거동인 목표 요레이트와 목표 횡슬립각을 계산한다. 산출된 목표 거동을 추종하기 위해 IVC에서는 차량 바디 관점에서의 제어량인 목표 요 모멘트와 횡력을 결정한다. 마지막으로 ODC에서는 IVC로부터 구한 목표 요 모멘트와 횡력을 생성하기 위한 각 시스템(ESC, AFS, RWS)의 제어량을 계산하여 분배한다. 추종해야 할 제어량의 우선 순위 그리고 각 시스템의 한계 성능 등을 고려한 최적화 기법을 이용하여 개별 시스템 제어량들을 결정하였다. 개발된 통합제어로직은 실제 양산차량을 개조한 시험차를 통해 고마찰 노면에서 그 성능을 검증하였다. IVO의 경우 기존 연구들을 활용하여 구현하였기 때문에 본 논문에서는 상세히 기술하지 않았다.5-8)
2. 샤시통합제어 로직 설계
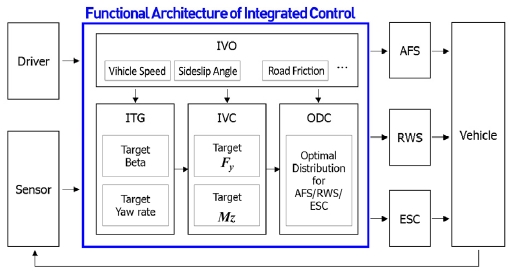
아래 Fig. 1은 통합제어 로직의 기능 아키텍처를 나타내고 있다. 통합제어 로직은 IVO, ITG, IVC 그리고 ODC 이렇게 4 가지 주요 모듈로 구성되어 있다. 지금부터 IVO를 제외한 모듈들에 대해 자세히 기술하도록 한다.
2.1 ITG : Integrated Target Generator
ITG는 센서 계측 신호와 IVO에서 추정된 신호를 이용하여 최적의 주행성능 구현을 위해 차량이 추종해야 할 목표 요 거동과 목표 횡 거동을 정의한다. 목표 요 거동(γd)은 센서로 측정된 운전자 조향각과 IVO로부터 추정된 차량 속도, 노면 마찰계수를 이용해 2자유도 바이시클 모델을 기반으로 다음과 같이 설계하였다.6)
| (1) |
여기에서, δf, lf, lr, Cf, Cr, M은 각각 운전자 조향각, 차량 무게 중심에서 앞/뒤 바퀴 거리, 앞/뒤 바퀴의 코너링 강성 그리고 차량 질량을 나타낸다.
목표 횡 거동은 차량의 횡슬립각을 기준으로 정의하였다. 목표 횡슬립각은 목표 요레이트와 같은 방식으로 바이시클 모델에 기반하여 설계가 가능하지만, 요 거동과는 달리 상시제어를 실시하지 않고 횡슬립각이 커진 경우 한시적으로 저감시키는 제어를 설계하기 위해 본 연구에서는 목표 횡슬립각을 0 deg로 정의하였다. 횡슬립각 0 deg는 차량의 Heading 방향과 주행 속도 궤적이 일치하는 것을 의미하며 운전자가 선회 안정감을 느끼는 이상적인 선회 상황으로 볼 수 있다.9)
2.2 IVC : Integrated Vehicle Controller
IVC는 앞 절에서 계산된 목표 요 거동과 목표 횡 거동을 추종하기 위한 차량 관점에서의 제어량인 목표 요 모멘트와 목표 횡력을 계산하는 모듈이다.
요레이트 제어의 경우 제어의 정확성도 중요하지만, 액추에이터의 응답지연을 보상하기 위해 비례-미분 제어를 많이 사용하게 된다. 하지만 미분 제어의 경우 요레이트 미분 값을 사용하기 때문에 노이즈 증폭 문제가 발생하며 본 연구에서는 이 문제를 회피하고자 수학적 모델 기반 요 모멘트 제어기를 설계하였다. 요 모멘트 제어기 구현을 위해 다음과 같이 바이시클 모델의 요레이트 동역학 모델을 사용하였다.
| (2) |
모델 기반 제어기의 경우 모델 파라미터 불확실성에 대한 고려가 필요하며, 이 부분에 대한 적절한 보상이 없으면 일관적인 제어 성능을 확보하기 어렵다. 모델 (2)의 파라미터 중 코너링 강성은 주행 상황에 따라 변동폭이 비교적 크며 모델의 정확도를 저하시키는 주요 인자이다. 따라서 이러한 코너링 강성의 불확실성에 대해 견실성을 보장할 수 있는 Sliding mode 제어 이론을 적용하여 목표 요 모멘트를 다음과 같이 산출하였다.6) 상세 유도 과정은 기존 연구결과를 참고바란다.6)
| (3) |
Where,
목표 횡 거동(횡슬립각) 추종을 위한 목표 횡력 연산의 경우 모델 기반 제어가 아닌, 단순 출력 신호 기반 비례 제어기(비례 게인 kp)를 설계하여 산출하였다.
| (4) |
실제 차량 주행 중 요레이트를 상시로 제어 할 경우 운전자에게 선회 성능이 개선됨을 느끼게 해주지만, 횡슬립각을 상시 제어 할 경우 운전자에게 선회 이질감을 발생시키는 문제가 발생하였다. 이러한 실험적 경험을 근거로, 본 논문에서는 요레이트의 경우 상시 제어하고, 횡슬립각 제어의 경우 횡슬립각이 과도하게 발생하는 상황에서만 작동하도록 제어 전략을 수립하였다. 따라서 요 모멘트 제어는 보다 빠른 응답성이 요구되기 때문에 이를 고려하여 Sliding mode 제어기를 설계하였고, 횡력 제어는 필요 시에 작동하면 되기 때문에 단순 출력 신호 기반의 비례 제어기로 설계하였다.
2.3 ODC : Optimal Distribution Controller
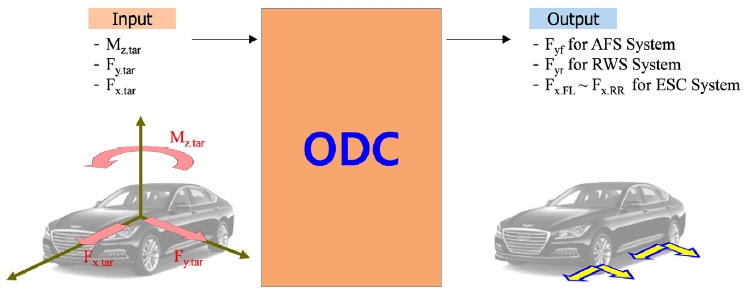
ODC에서는 IVC로부터 연산된 제어량인 목표 요 모멘트와 목표 횡력을 구현하기 위한 각 시스템(ESC, AFS, RWS)의 분배 제어 값을 실시간 계산한다. ESC 시스템은 각 바퀴의 타이어 종력 그리고 AFS/RWS 시스템은 전/후륜 타이어 횡력을 발생시키기 때문에 ODC에서는 각 시스템에 필요한 제어 입력 값을 종/횡 타이어 힘을 기준으로 결정한다. 연산된 종/횡 타이어 힘은 개별시스템 제어값을 결정하는데 사용된다. Fig. 2와 같이 ODC는 IVC에서 계산된 목표 요 모멘트(Mz.tar), 목표 횡력(Fy.tar) 그리고 목표 종력(Fx.tar) 총 3개의 제어량을 입력 받아, 이를 만족하는 전륜 횡력, 후륜 횡력 그리고 각 바퀴의 제동력 총 6개의 타이어 힘을 산출한다. 타이어 힘 연산 시 제어량(Mz.tar, Fy.tar, Fx.tar)들의 추종 성능을 최적으로 만족시키고, 동시에 시스템(AFS, RWS, ESC)의 성능 한계를 고려해야 하기 때문에 최적화 방법을 통하여 ODC를 설계하였다. 목표 종력(Fx.tar)의 경우 현재는 적극적으로 사용하지 않는 제어 요소지만, 향후 속도 제어 필요성으로 인해 목표 종력이 신규 추가가 되었을 경우 본 모듈을 그대로 사용할 수 있도록 목표 종력을 추가 고려하여 설계하였다. 따라서 ODC로 입력되는 목표 종력은 현재 0으로 설정하였다.
최적화 구현을 위해 우선 입력 제어량 간의 제어 우선순위를 결정하였다. 차량의 요 거동은 핸들링 성능에 가장 중요한 요소이기 때문에 Mz.tar 추종을 최우선으로 두고, 그 다음으로 Fy.tar 와 Fx.tar 는 동등하게 우선권을 부여하였다. 즉, Mz.tar을 추종하는 범위 내에서 Fy.tar 와 Fx.tar 를 최대한 추종하도록 하는 것이 본 최적화의 목표이다.
그 다음으로 제어 시스템들의 성능 한계를 고려하였다. AFS와 RWS 목표 조향각 같은 경우 타이어 각 기준으로 +/-3 deg를 넘지 않아야 하고, ESC의 제동은 타이어 종력 기준으로 0보다 크지 않고 제동에 의한 일정 슬립률(0.1)을 초과하지 않아야 한다. AFS와 RWS의 경우 하드웨어적으로는 타이어 각을 5 deg 이상을 작동시킬 수 있지만, 액추에이터 고장 시 안정성 확보를 위해 3 deg 이내로 제한하였다. ESC의 경우 제동이기 때문에 타이어 종력은 0보다 작아야 하고, 제동에 의한 과슬립을 방지하기 위해 슬립률 0.1을 넘지 않게 제동력을 제한하였다.
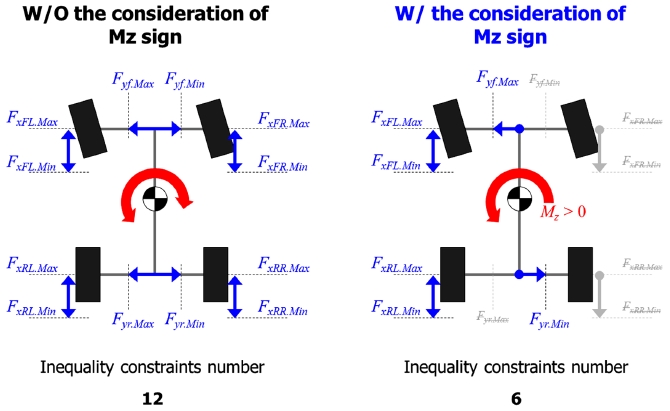
지금까지 최적화 구현을 위해 최적화의 목표 그리고 제약 사항들에 대해 서술하였다. 하지만 위에서 서술한 제약 사항들은 Inequality 제약 사항으로 최적해를 구하기 위해 반복연산을 해야 한다. 산술적으로 n개의 Inequality 제약 조건이 있는 경우 2n번 만큼의 반복 연산이 필요하다. 이는 연산 부하를 과도하게 만들어 실시간 작동성에 문제를 일으키게 된다. 이러한 연산 부하 문제를 최소화하기 위해 Mz.tar 의 부호 별로 최적화를 분리하였다. 아래 Fig. 3은 Mz.tar 부호 별 고려해야 할 제약 조건의 수를 나타내고 있다. 그림과 같이 Mz.tar 의 부호를 고려하지 않을 경우 12개의 제약 조건이 나오게 되고, 고려할 경우 6개의 제약 조건이 나오게 된다. 즉 부호를 고려하지 않은 경우가 고려한 경우보다 64(=26)배의 연산부하를 가지게 된다.
Mz.tar 부호를 고려한다고 해도 6개의 제약조건은 64번의 반복연산으로 연산부하가 크기 때문에 본 논문에서는 ESC의 각 바퀴 제동 중 후륜 제동은 사용하지 않았다. 이는 급격한 선회로 인해 차량이 불안정한 경우 대부분 Oversteer가 발생하며 이를 방지하기 위해 전륜 제동이 효과적이라는 경험 및 기존 연구10)에 근거하여 결정하였다. 위에 서술한 내용을 바탕으로 Mz.tar가 양수일 경우 최적화 문제를 설계하기 위해 목적 함수와 제약 조건들을 아래와 같이 정의하였다.
| (5) |
여기에서, FxFL.tar, Fyf.tar, Fyr.tar은 최적화를 통해 결정해야 할 각 휠의 요구 타이어 힘(시스템 제어 값)이고, Mz.tar, Fx.tar, Fy.tar은 상위 모듈 IVC에서 연산된 제어량 들이다. Cf, Cr, Ci는 전/후륜 코너링 강성 그리고 종방향 힘 강성을 의미한다. 식 (5)에서 보이는 바와 같이 최적화 목적 함수를 시스템 제어 값인 FxFL.tar, Fyf.tar 그리고 Fyr.tar가 IVC 제어량인 Fy.tar과 Fx.tar을 최대한 추종하도록 정의하였고, 제어 우선순위가 가장 높은 Mz.tar은 Equality 제약 조건으로 정의하였다. 이는 Mz.tar은 반드시 추종해야 할 제어량이고 Fy.tar과 Fx.tar은 Mz.tar의 추종이 만족되고, 기타 다른 제약 조건들이 만족되는 범위 내에서 최대한 추종하도록 하기 위함이다. 최적해를 구하기 위해 식 (5)에 대한 Hamiltonian을 아래와 같이 정의하였다.11)
| (6) |
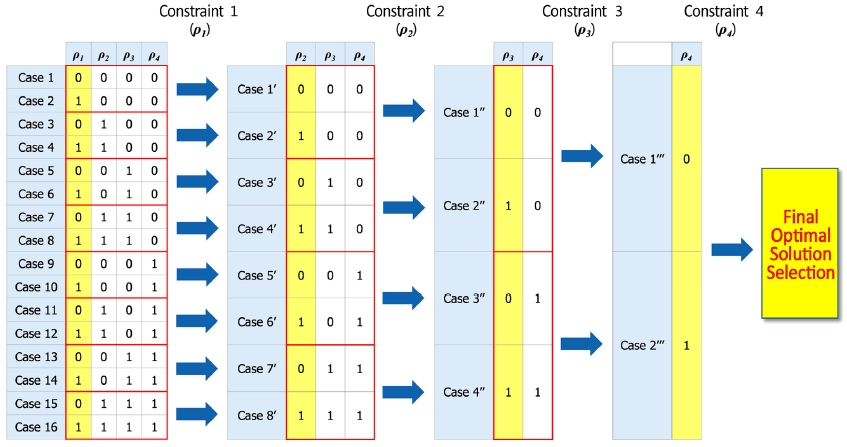
식 (6)에 대한 최적해는 최적화 Solver(Forces Pro, fmincon 등)를 통해 구할 수 있지만 이러한 방식은 반복 연산(Iteration)과정을 거치기 때문에 ECU 적용 시 연산 부하가 과다할 우려가 있다. 이를 극복하기 위해 본 논문에서는 반복 연산 없이 최적해를 산출하였다. 식 (6)을 보면, Inequality 제약 조건의 수가 4개로 총 16개(=24)의 경우의 수가 나오게 된다. 최적해는 우선 모든 경우(16개)에 대한 해들을 일괄적으로 구하고, 그 해들이 제약 조건을 만족하는지를 판단하여 선택하는 방식으로 산출하였다. 식 (6)에서 ρi와 ci(i=1~4)는 Inequality 제약 조건을 풀기 위한 변수로, ρi는 0과 1중에 하나의 값을 가지고, ci는 0과 0이 아닌 값을 가지게 된다. ρi가 0이면 현재 구한 최적해의 값이 제약조건을 만족한다는 의미로 ci는 0이 아닌 값을 가지게 된다. 이럴 경우 해당 Inequality 제약 조건은 무시할 수 있다. 반대로 ρi가 1이면 현재 구한 최적해의 값이 제약 조건을 만족하지 못한다는 의미로(제약조건의 범위를 초과) ci는 0의 값을 가지게 된다. 이럴 경우 해당 Inequality 제약 조건은 Equality 제약 조건으로 변경된다. 즉, ρi의 값에 관계 없이 식 (6)의 Inequality 제약 조건은 사라지게 된다. Inequality 제약 조건이 없는 최적화는 단순 First-order necessary condition을 이용하여 구현할 수 있다. 총 4개의 ρ에 대한 모든 경우의 수는 총 16(=24) 개이다. 모든 경우가 Inequality 제약 조건이 없기 때문에, Lagrange multiplier method(=first-order necessary condition)를 이용하여 최적해를 구할 수 있다. 이렇게 구해진 16개의 해들 중 최적해를 선정하기 위해 아래 Fig. 4와 같이 연산된 모든 경우의 해들을 Inequality 제약 조건들과 비교하였다. 아래 Fig. 4에서 Case1 ~ Case 16은 First-order necessary condition을 통해 계산된 해들을 의미한다. 예를 들어 Case1은 최적해가 모든 Inequality 제약 조건을 만족한다는 가정하에 연산된 최적해이고, Case 2는 1번의 Inequality 제약 조건을 제외한 나머지 조건들이 만족한다는 가정하에 연산된 최적해이다. 하지만, 제약 조건에 대한 만족 여부를 가정하여, 만족 시 제약 조건을 무시하고, 불만족 시에는 Equality 제약 조건으로 변경하여 최적해를 구했기 때문에 그 결과가 해당 제약 조건을 만족한다고 할 수 없다. 따라서 모든 경우의 최적해(Case 1 ~ Case 16)들이 Inequality 제약조건을 만족하는지 여부를 판단해야 한다. Fig. 4의 왼쪽 표에 표현된 각 Case들의 배열을 보면 2개 Case 씩 1번 제약 조건에 대한 가정(ρ1)만 다르고 나머지는 같음을 알 수 있다. 따라서 총 16개의 해들을 1번 제약 조건에 대해 비교를 하면 8개의 해를 선정할 수 있다. 선정된 8개의 해를 2번 제약조건에 대해 비교하면 4개의 해가 선정된다. 같은 방식으로 3번과 4번에 대한 제약 조건을 비교하면 최종 최적해를 구할 수 있다. 지금까지 Mz.tar가 양수일 경우 최적해를 구하는 방법에 대해 서술하였다. Mz.tar이 음수일 경우 제동 시스템 제어값에 대한 변수만 바뀌고(FxFL.tar →FxFR.tar) 동일한 방식으로 구하면 되기 때문에 생략하도록 한다.
3. 시뮬레이션 및 실차 검증
앞서 개발한 통합제어 평가를 위해 시뮬레이션 해석 및 실차 검증을 실시하였다. 주로 차량 횡방향 안정성의 향상도를 검증하였으며 선회 불안정 상황인 급격한 차선 변경 시 차량 요 거동과 횡슬립각을 분석하였다. 시뮬레이션 해석에서는 차량 모델로 차량해석SW인 CARSIM을 사용하였고 본 연구에서 제안된 최적화 방법론과 상용 최적화 알고리즘을 차량 제어 성능 관점에서 비교 검증하였다.
3.1 시뮬레이션 검증
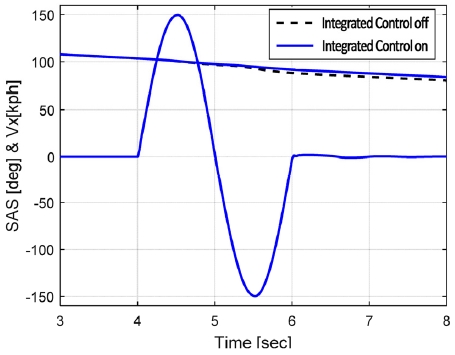
통합제어에 의한 차량 안정성 확보 여부를 판단하기 위해, Fig. 5와 같이 차속 100 kph에서 급격한 Open-loop 조향 입력의 Single lane change를 수행 하였다.
제안된 통합제어의 효과를 파악하기 위해 통합제어 On/off 결과를 비교하였다. 또한, 제안된 최적화 로직의 타당성을 검증하기 위해 비선형 최적화 Solver인 Matlab의 Fmincon 수행 결과도 같이 비교하였다.
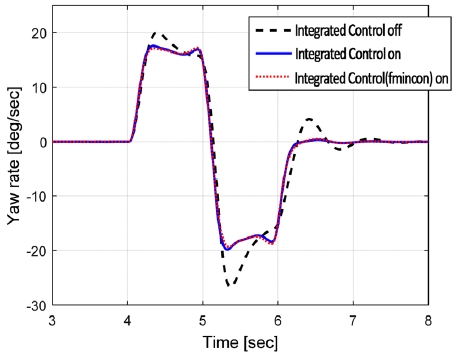
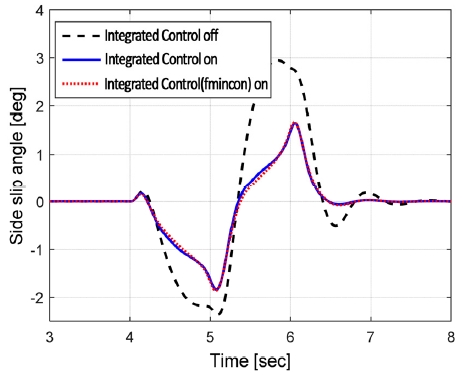
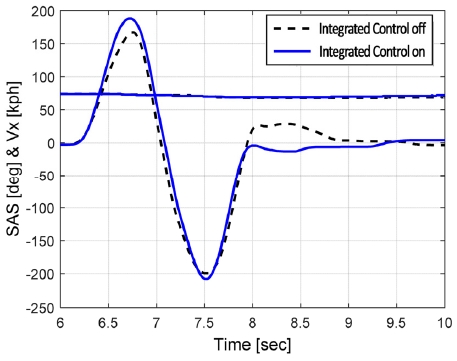
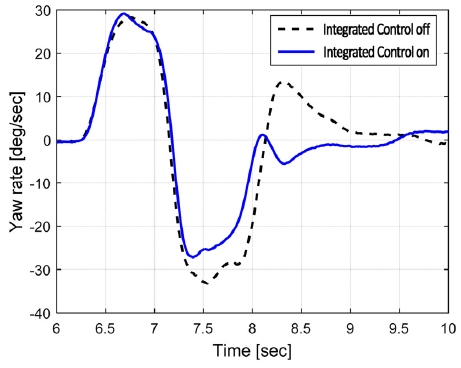
Fig. 5는 시뮬레이션 상의 주행 시나리오로 Open-loop 운전자 조향각 입력과 통합제어 On/off 시의 주행 속도를 나타내고 있다. 동일한 조향 및 초기차속 조건에서 제안된 통합제어를 통해 차량의 요 및 횡 안정성이 통합제어 Off 대비 크게 개선됨을 Figs. 6~7을 통해 확인할 수 있다.
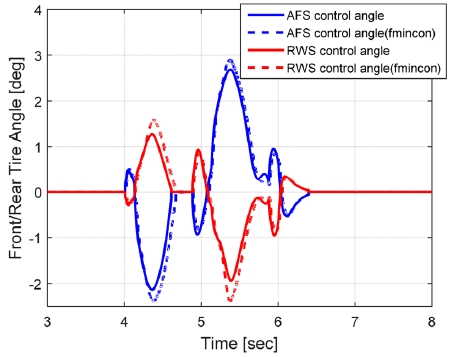
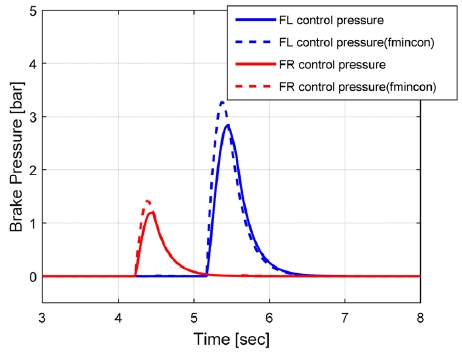
또한, 본 논문에서 제안한 최적화 방법론의 타당성을 검증하기 위해 범용 최적화 Solver인 Fmincon을 적용하여 성능을 비교 하였다. Figs. 6~9와 같이 제안한 최적화 결과와 범용 최적화를 사용한 결과가 산출 제어량 측면에서의 큰 차이가 없으며 특히 차량 안정성 제어 측면에서 차량 거동은 거의 동일함을 확인할 수 있었다. 두 방식에 대한 수행시간을 측정한 결과 본 논문에서 제안한 방식이 범용 Solver를 사용한 경우보다 10배 이상 빠름을 확인하였다.
결국 제안된 최적화 알고리즘은 범용 Solver(Fmincon)와 동등 수준의 차량 제어 성능을 보이며 수행 시간 측면에서 10배 이상의 이득이 있음을 확인할 수 있었다.
3.2 실차 검증
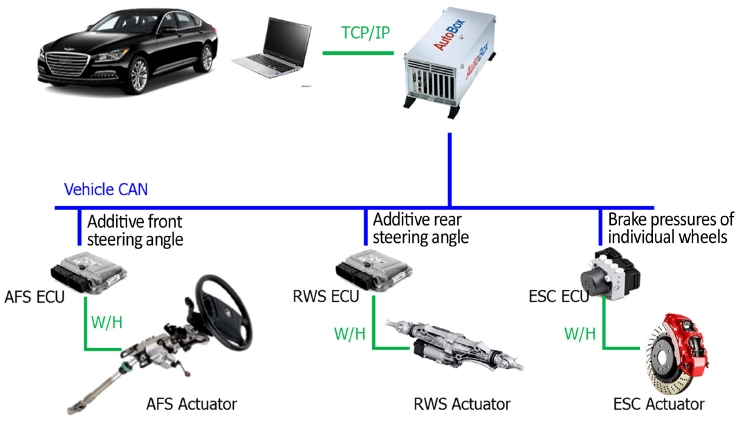
본 연구에서 개발한 통합제어 로직의 실차 검증을 위해 Fig. 10과 같이 시험차를 구성하였다. 보는 바와 같이 현대 제네시스 AWD 양산차량에 AFS와 RWS 시스템을 추가 장착하였다. 통합제어 로직은 Rapid control prototype(RCP) 장비인 dSPACE사의 AutoBox를 활용하였다.
시험차 구성 후 고마찰로에서 통합제어에 의한 차량 안정성 확보 여부를 판단하기 위해 급격한 Single lane change 실시하였다. 통합제어의 효과를 파악하기 위해 통합제어 On/off 결과를 비교하였다.
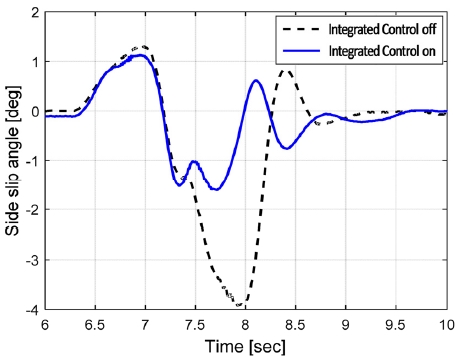
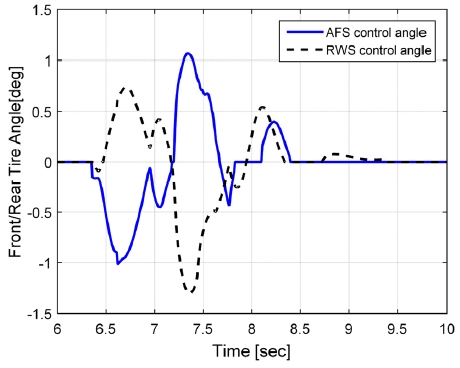
아래 Fig. 11은 시험 시나리오로 통합제어 On/off 시의 주행 속도와 운전자 조향각을 나타내고 있다. 차속 80 kph에서 급격한 조향을 하는 경우로 점선은 통합제어 Off를 실선은 통합제어 On인 경우의 조향각과 차속을 나타내고 있다. 통합제어 On 경우 Off보다 동일 속도 주행 상황에서 다소 더 과한 운전자 조향이 입력되고 있음을 알 수 있다. 그럼에도 불구하고 통합제어를 통해 차량의 요 및 횡 안정성이 개선됨을 Figs. 12~14를 통해 확인할 수 있다. 보다 자세히 설명하면 통합제어 동작 시 횡안정성 확보를 위한 요레이트 반대방향 AFS 제어각과 정방향 RWS 제어각의 효과를 통해 요레이트의 Peak2peak가 Off대비 62 deg/sec에서 56 deg/sec로 대략 9 %가 개선이 되었고, 조향입력 수렴 후(대략 8 sec 부근) 요레이트의 수렴 시간(2 deg/s 이내)이 980 ms에서 600 ms로 대략 42 % 개선된 결과를 보이고 있다. 횡슬립각 또한 Peak2peak가 5.2 deg에서 2.7 deg로 48 %가 개선됨을 확인할 수 있다.
4. 결 론
본 논문에서는 샤시제어 시스템인 AFS, RWS, ESC시스템들의 통합을 통해 차량의 횡방향 안정성 향상을 목적으로 하는 통합제어 로직을 개발하였다. 개발한 통합제어 로직은 IVO, ITG, IVC 그리고 ODC 4개의 모듈로 구성되는데, ITG에서는 최적 주행 성능을 위한 차량의 목표 거동인 목표 요레이트와, 목표 횡슬립각을 연산하고, IVC 에서는 목표 거동을 추종하기 위한 차량 관점에서의 제어량인 Mz와 Fy를 산출한다. 마지막으로 ODC에서는 앞서 산출된 Mz와 Fy를 추종하기 위한 각 시스템들의 분배 제어량을 최적화를 통해 결정하였다. Mz와 Fy 사이의 제어 우선권, 각 개별 시스템의 성능 한계, 그리고 연산 부하를 고려하여 최적화 문제를 정의하였고 이를 통해 실시간 연산을 통해 개별 시스템 타이어 요구 힘으로 분배하였다.
개발된 통합제어 로직은 RCP 환경에 구현, 적용되었으며 고마찰로 시뮬레이션 해석 및 실차 시험을 통해 그 성능 및 타당성을 검증하였다. 평가 결과 개발된 통합제어 로직의 적용으로 차량의 횡방향 안정성 및 수렴성이 개선됨을 확인하였다. 향후에는 RCP 기반으로 개발된 통합제어 로직을 ECU 레벨로 개발하기 위한 연구들을 수행하고, 통합제어 로직의 신뢰성 확보를 위한 Fail-safe 로직을 개발할 예정이다.
Acknowledgments
본 연구는 현대자동차의 연구 지원을 통해 수행되었음. 이 성과는 2019년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(2017R1A1A1A05069503). 또한, 이 논문은 2019년도 한국기술교육대학교 교수 교육연구진흥과제 지원에 의하여 연구되었음.
References
- Y. Hattori, K. Koibuchi, and T. Yokoyama, “Force and Moment Control with Nonlinear Optimum Distribution for Vehicle Dynamics”, Proceedings of the 6th International Symposium on Advanced Vehicle Control, p595-600, (2002).
-
P. Koehn, and M. Eckrich, “Active Steering - The BMW Approach Towards Modern Steering Technology”, SAE 2004-01-1105, (2004).
[https://doi.org/10.4271/2004-01-1105]

-
E. Ono, Y. Hattori, Y. Muragishi, and K. Koibuchi, “Vehicle Dynamics Integrated Control for Four-wheel-distributed Steering and Four-wheel-distributed Traction/Braking Systems”, Vehicle System Dynamics, 44(2), p139-151, (2006).
[https://doi.org/10.1080/00423110500385790]

-
J. Wang, and R. G. Longoria, “Coordinated Vehicle Dynamics Control with Control Distribution”, Proceeding of the 2006 American Control Conference, (2006).
[https://doi.org/10.1109/acc.2006.1657573]

-
K. Yi, K. Hedrick, and S. -C. Lee, “Estimation of Tire-road Friction Using Observer Based Identifiers”, Vehicle System Dynamics, 31(4), p233-261, (1999).
[https://doi.org/10.1076/vesd.31.4.233.4231]

- W. Cho, J. Yoon, S. Yim, B. Koo, and K. Yi, “Estimation of Tire Forces for Application to Vehicle Stability Control”, IEEE Transactions on Vehicular Technology, 59(2), p638-649, (2010).
-
W. Cho, and M. Hyun, “Estimation of Road Bank Angle and Vehicle Side Slip Angle Using Bayesian Tracking and Kalman Filter Approach”, Int. J. Automotive Technology, 19(6), p993-1000, (2018).
[https://doi.org/10.1007/s12239-018-0096-y]

-
S. -H. You, J. -O. Hahn, and H. C. Lee, “New Adaptive Approaches to Real-time Estimation of Vehicle Sideslip Angle”, Control Engineering Practice, 17(12), p1367-1379, (2009).
[https://doi.org/10.1016/j.conengprac.2009.07.002]

-
S. Horiuchi, K. Okada, and S. Nohtomi, “Improvement of Vehicle Handling by Nonlinear Integrated Control of Four Wheel Steering and Four Wheel Torque”, JSAE Review, 20(4), p459-464, (1999).
[https://doi.org/10.1016/s0389-4304(99)00051-x]

-
S. -H. You, J. -S. Jo, S. Yoo, J. -O. Hahn, and K. I. Lee, “Vehicle Lateral Stability Management using Gain-Scheduled Robust Control”, Journal of Mechanical Science and Technology, 20(11), p1898-1913, (2006).
[https://doi.org/10.1007/bf03027583]

- W. Cho, J. Yoon, J. Kim, J. Hur, and K. Yi, “An Investigation into Unified Chassis Control Scheme for Optimized Vehicle Stability and Maneuverability”, Vehicle System Dynamics, 46(1), p87-105, (2008).