공기압축기 로터 어셈블리 형상의 개선 설계와 피로수명 예측

1. 서 론

연료전지 자동차(FCEV, Fuel Cell Electric Vehicle)는 수소와 산소의 전기화학 반응으로 발생하는 전기에너지를 동력원으로 사용한다.

이러한 연료전지 자동차의 운전 장치 시스템(BOP, Balance of Plant)은 수소 공급계(FPS, Fuel Processing System), 공기 공급계(APS, Air Processing System) 및 열 관리계(TMS, Thermal Management System)로 구성된다.¹⁾ 연료전지 자동차에서 사용되는 수소와 산소는 각각 고압의 수소탱크와 공기 공급계의 공기압축기를 통하여 공급을 받는다. 이때, 공기압축기는 연료전지 자동차의 성능에 큰 영향을 줌에 따라 많은 연구가 진행되어 왔다.

이용복 등²⁾은 연료전지 용 에어 블로워의 내구성과 안전성을 실험적으로 연구를 수행하였다. 실험 결과, 설계 수치와 유사하게 도출되었으며 내구성 실험 동안 에어 블로워의 공력 성능과 소모 동력이 일정하게 유지되었다. 하경구 등³⁾은 연료전지 자동차에 적용되는 공기압축기의 구조 및 유동해석을 진행하고, 그 결과를 통해 소요 전력을 줄일 수 있는 개선안을 도출하였다. 육지용 등⁴⁾은 유한요소해석과 동특성 시험을 통해 연료전지 자동차에 적용되는 공기압축기 회전부의 구조적 안정성, 회전시스템의 동특성 및 구조적 진동 특성을 분석하였다. Zheng⁵⁾는 공기압축기 임펠러의 형상에 따른 강도와 변형량을 해석을 통해 연구하였다. 이 연구에서는 임펠러 끝단의 두께, 후방 디스크 두께, 후방 디스크 높이, 필렛 반경 및 임펠러 내부의 반경을 설계변수로 사용하였다. 연구 결과, 다섯 가지 설계변수 중 임펠러 끝단의 두께, 후방 디스크 두께 및 임펠러 내부의 반경의 크기가 임펠러의 강도와 변형량에 중요한 역할을 한다는 것을 확인하였다. 양현섭 등⁶⁾은 고속 볼 베어링을 적용한 에어 블로워의 NVH 문제 개선을 위해, 회전체 개선 설계 방향 및 결과를 실험을 통하여 연구하였다. 강현수 등⁷⁾은 원심압축기 임펠러 블레이드 형상에 대해 유체-구조 연성해석을 통해 유체역학적 성능과 구조역학적 안전성을 검토하였고, 응답 표면법을 이용하여 임펠러의 효율적인 최적설계방안을 제시하였다. 이들은 입구 폭, 블레이드 두께, 입구 각도 및 출구 각도를 설계변수로 사용하였으며, 각 설계변수에 따라 압력 비, 변위 및 최대응력의 경향을 관찰하고 최적의 임펠러 형상을 도출하였다. Liu 등⁸⁾은 원심압축기의 임펠러에 대해 원심력과 공기역학적 성능이 임펠러의 피로수명에 어떠한 영향을 끼치는지 해석적 연구를 진행하였다. 이 연구에서는 Soderberg, Goodman 및 Smith 피로 이론을 사용하여 피로수명을 구하였고 실제 실험값과 비교하였다.

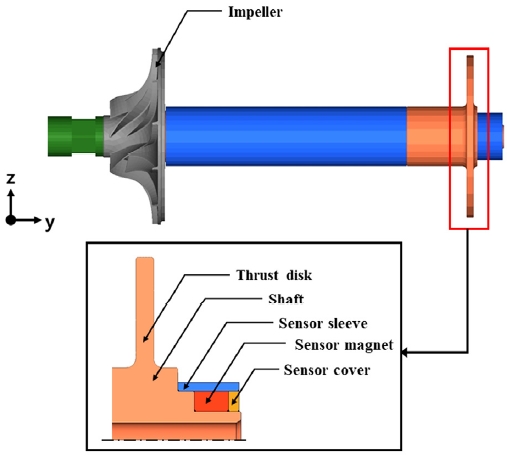
공기압축기는 흡입된 공기를 원하는 압력 및 유량으로 압축하는 임펠러(Impeller)와 고속 회전하는 축을 지지하는 샤프트의 쓰러스트 디스크(Thrust disk)와 센서부(Sensor components) 등으로 구성된다(Fig. 1). 이때, 임펠러, 쓰러스트 디스크 및 센서부에 작용하는 응력은 고속회전에 의한 원심력과 구성 부품의 기하학적 형상에 의하여 영향을 받는다.

Fig. 1

Schematic diagram of air compressor rotor assembly

본 연구에서는 연료전지 자동차에서 사용될 개발 중인 공기 압축기 로터 어셈블리의 구성 부품의 형상 변경에 따른 구조 안전성을 평가함으로써 최적의 설계 변수 크기를 결정하였다. 그 이후 정지 상태와 최대속도 125 krpm으로 운전을 반복하는 경우에 대하여 개발 중인 로터 어셈블리의 피로수명을 예측하였다. 이 과정에서 최대속도가 100 krpm이며 개발 완료된 로터 어셈블리에서 해석과 실험으로 측정한 피로수명이 서로 가장 유사한 결과가 나타난 방법으로 평균응력을 보정하였다.

공기압축기의 모델링, 구조해석 및 피로해석을 위해서, 각각 ANSYS Meshing, ANSYS Mechanical 및 ANSYS nCode DesignLife 등의 상용 프로그램을 사용하였다.

2. 유한요소 모델링 및 구조해석 조건

2.1 유한요소 모델링

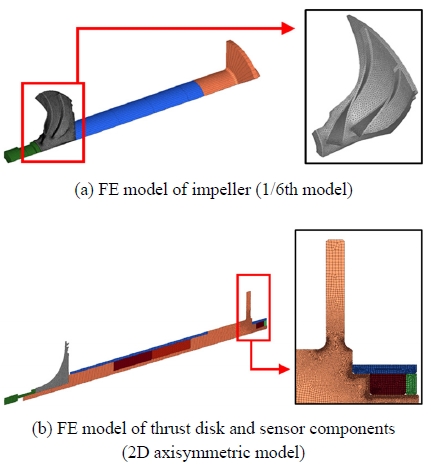
공기압축기 로터 어셈블리의 임펠러는 고속 회전을 통하여 외부의 공기를 흡입하여 압축하는 역할을 한다. 본 연구에서 사용한 임펠러의 구조는 각각 6개의 풀 블레이드와 스플리터 블레이드로 구성된다. 구조해석에 사용된 임펠러 유한요소해석 모델은 해석시간을 단축하기 위해 전체 모델을 사용하지 않고 풀 블레이드와 스플리터 블레이드를 기준으로 1/6회전 대칭 모델을 사용하였다. 해석에 사용된 임펠러의 유한요소는 10 node-Tetra 타입을 사용하였고, 사용한 요소 개수는 총 167,894개 이상이다.

쓰러스트 디스크는 고속 회전하는 회전축을 지지하는 역할을 한다. 센서부는 로터 어셈블리의 위치(위상각)를 측정하여 속도를 제어하는 역할을 한다. 구조해석에 사용된 쓰러스트 디스크와 센서부의 유한요소해석 모델은 해석시간을 단축하기 위해 이차원 축대칭 모델을 사용하였다. 쓰러스트 디스크와 센서부는 임펠러와 서로 멀리 떨어져 있기 때문에, 임펠러를 정확하게 모델링하지 않아도 쓰러스트 디스크와 센서부의 구조해석에 큰 영향을 미치지 않는다. 따라서 쓰러스트 디스크와 센서부를 이차원 축대칭으로 모델링할 때에는, 임펠러 형상을 단순화하여 임펠러도 이차원 축대칭으로 모델링하였다. 쓰러스트 디스크와 센서부의 유한요소는 6 node-Tria와 8 node-Quad 타입을 사용하였고, 사용한 요소 개수는 각각 14,404개와 41,071개 이상이다. 임펠러와 쓰러스트 디스크 및 센서부의 유한요소 모델을 Fig. 2에 도시하였다.

Fig. 2

FE models of impeller, thrust disk and sensor components

2.2 구조해석 조건

구조해석에서는 부품간의 접촉 조건, 경계 조건, 하중 조건의 설정이 매우 중요하다. 본 연구에서는 이들 조건을 다음과 같이 설정하였다.

공기압축기 구성 부품 사이의 접촉 조건은 단순 접촉면으로 가정하고 마찰 조건을 사용하였다. 마찰계수는 접촉되는 재료에 따라 다음과 같이 세 가지로 분류하여 설정하였다; 0.33(강재-알루미늄 접촉 면), 0.31(강재-강재 접촉 면), 0.1(그 외의 모든 접촉 면).⁹⁾ 또한 센서부에 들어가는 자석과 슬리브는 서로 끼워맞춤으로 체결이 되므로 이를 반영하기 위하여 Interference Fit 조건을 사용하였다.

경계 조건으로는 Fig. 1의 센서부 부근의 회전축 상의 한 점을 3 자유도 변위 구속을 하고, 임펠러 부근의 회전축 상의 한 점을 회전축 방향을 제외한 나머지 2 자유도 변위 구속을 하였다. 하중 조건은 공기압축기의 최대 회전속도인 125 krpm을 사용하였다.

구조해석에 사용된 공기압축기 구성 부품의 기계적 물성을 Table 1에 정리하였다.

Table 1

Material properties of constituting components of air compressor

3. 형상 개선 설계

ANSYS사의 Meshing과 Mechanical 등의 상용 프로그램을 이용하여 공기압축기를 구성하는 임펠러, 샤프트 등을 모델링 및 구조해석을 수행하였다.^10,11)

3.1 임펠러의 형상 개선 설계

3.1.1 임펠러의 설계변수

회전에 의하여 임펠러에 발생하는 응력은 회전 속도, 임펠러 디스크 형상 및 임펠러 날개의 형상 등에 따라 좌우된다.

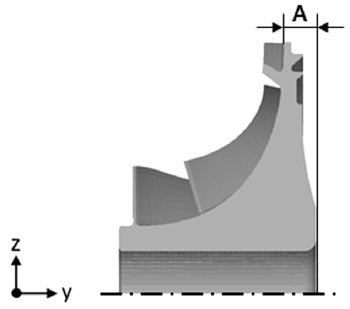
본 연구에서는 임펠러 디스크의 후방 두께(A)를 설계 변수로 고려하였다(Fig. 3). 그 이유는 매우 빠른 속도로 회전하는 임펠러의 단면 형상은 좌우대칭으로 하는 것이 응력 분포 측면에서 유리한데, 임펠러 디스크의 후방 두께를 증가시키면 초기 형상보다 좌우대칭인 형상에 더욱 가까워지기 때문이다.

Fig. 3

Rear disk thickness (A) of impeller

임펠러 디스크의 후방 두께(A)를 초기 설계 값인 2.8로부터 4.3, 5.8, 7.3 및 8.8 mm로 증가시키면서 구조해석을 수행하였다.

3.1.2 초기 설계 상태에서의 응력 해석 결과

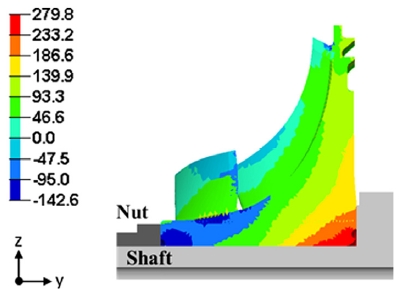
초기 설계 상태(A=2.8mm)에 대한 임펠러의 구조해석 결과를 Fig. 4에 도시하였다. 초기 설계 상태에서, 임펠러의 최대응력은 279.8MPa로 회전축과 닿아 있는 내부 표면에서 발생하였다. 회전축으로부터 거리가 멀어 질수록 응력의 크기가 작아지는 것을 알 수 있다. 또한 회전축으로부터 동일한 반경 방향의 거리만큼 떨어진 경우에는, 중앙보다 좌우 끝단에서의 응력이 더 큰 것을 확인하였다. 이는, 임펠러의 좌우 끝단이 너트와 샤프트를 사용한 조임으로 고정되기 때문이다(Fig. 4).

Fig. 4

Von Mises stress distribution of impeller (unit: MPa)

3.1.3 최대응력을 고려한 형상 개선 설계

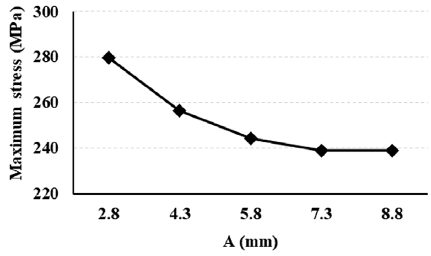
임펠러 디스크의 후방 두께 크기를 변화시키면서(A=4.3, 5.8, 7.3 및 8.8 mm), 각각의 경우에 대하여 구조해석을 수행하였다. 임펠러 디스크의 후방 두께 변화에 따른 임펠러에서의 최대 응력을 Fig. 5에 나타내었다. 임펠러 후방 디스크의 두께가 증가할수록 최대 응력이 감소하지만, 임펠러 디스크의 후방 두께가 증가함에 따라서 그 감소 폭이 점점 작아짐을 확인하였다. 임펠러 디스크의 후방 두께가 A=5.8 mm과 같거나 더 클 때에는, 임펠러 디스크의 후방 두께가 증가하여도 최대 응력의 변화는 미미함을 확인하였다. 그 이유는 후방 두께가 A=5.8 mm가 될 때, 임펠러 디스크의 단면 형상이 좌우대칭에 가까워지기 때문이다.

Fig. 5

Change in maximum von Mises stress with respect to rear disk thickness (A) of impeller

3.1.4 변위를 고려한 형상 개선 설계

고속 회전 운동을 하는 임펠러에서는 변형이 발생한다. 많은 경우에 임펠러 블레이드 끝단과 하우징 사이의 간극이 매우 작기 때문에, 임펠러에서 발생하는 변형은 반드시 고려되어야 한다.

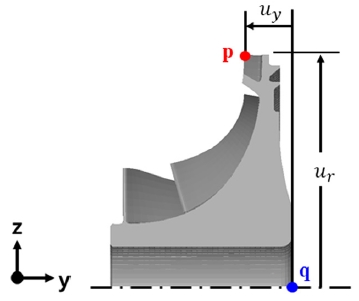
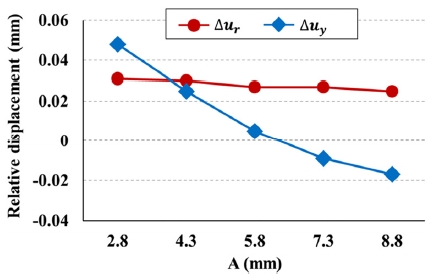
본 연구에서는 여러 크기의 임펠러 디스크 후방 두께에서, 공기압축기 회전 전과 최대 회전속도(125 krpm)로 회전할 때에 Fig. 6의 점 q에 대한 점 p의 반경 방향의 상대변위(Δu_r)와 회전축 방향의 상대변위(Δu_y)가 어떻게 변화하는지 계산하여, 이들을 Fig. 7에 도시하였다.

Fig. 6

The relative displacements of impeller at two points

Fig. 7

Change in the relative displacements with respect to rear disk thickness (A) of impeller

임펠러 디스크의 후방 두께가 변화하여도, 반경 방향의 상대변위(Δu_r)는 크게 변화하지 않음을 확인하였다. 그러나 임펠러 디스크의 후방 두께가 증가함에 따라서, 축방향의 상대변위(Δu_y)는 0.048 mm에서 -0.017 mm로 점차 감소하였다. 회전 전과 최대 회전속도로 회전할 때, 상대변위의 변화가 작아야 임펠러 블레이드와 하우징 사이의 간섭을 방지할 수 있다. 따라서 Fig. 7로부터 임펠러 디스크의 후방 두께가 A=5.8 mm일 때, 임펠러 블레이드와 하우징 사이의 간섭 가능성이 가장 작음을 확인할 수 있다.

3.2 쓰러스트 디스크 및 센서부의 형상 개선 설계

3.2.1 쓰러스트 디스크 및 센서부의 설계변수

본 연구에서는 쓰러스트 디스크 및 센서부에서 모두 세 개의 설계 변수를 사용하였다(Fig. 8). 센서 슬리브의 길이(L1), 쓰러스트 디스크의 후방 길이(L₂) 및 센서 슬리브 압입량(S_in). L₁=8.5, L₂=1.40 및 S_in=0.01 mm인 경우를 초기 설계 상태(Baseline case)로 하고, 이 값으로부터 세 설계변수 L₁, L₂ 및 S_in의 크기를 Table 2에서와 같이 변경하면서 각각의 경우에 대하여 해석을 수행하였다.

Fig. 8

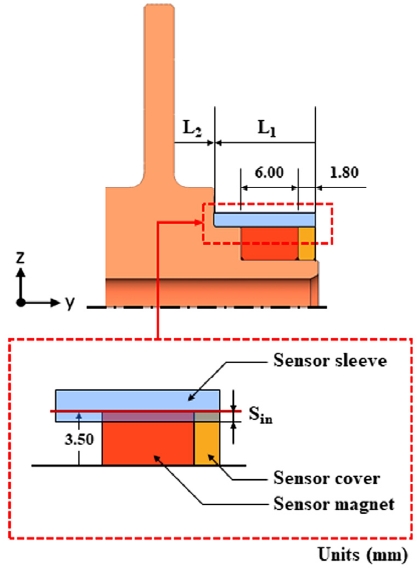
Three design variables near thrust disk and sensor components; sensor sleeve length (L1), thrust disk rear length (L2) and sensor sleeve interference fit depth (Sin)

Table 2

Design variables and their magnitudes near thrust disk and sensor components

3.2.2 초기 설계 상태에서의 응력 해석 결과

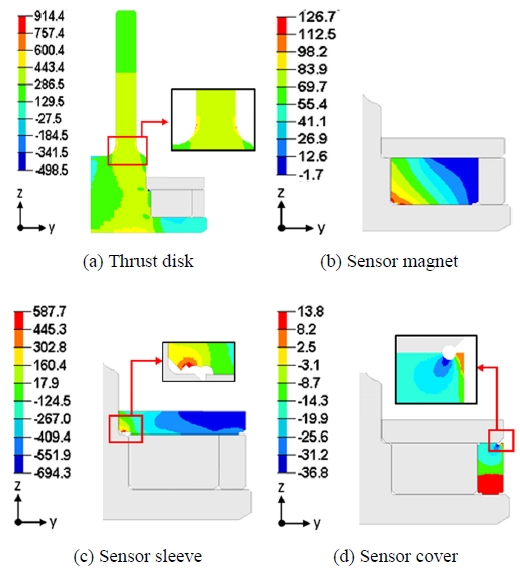
초기 설계 상태(L₁=8.5, L₂=1.40 및 S_in=0.01 mm)의 구조해석 결과를 Fig. 9에 도시하였다. 쓰러스트 디스크, 센서 슬리브 및 센서 커버는 연성재료이므로 Signed von Mises stress를 도시하였고 센서 마그넷은 취성재료이므로 Maximum principle stress를 도시하였다(Fig. 9). 쓰러스트 디스크에서 최대응력은 필렛 주위에서 발생하며 크기는 914.4 MPa로, 소재의 극한응력 1,070 MPa과 항복응력 1,000 MPa에 미치지 못하였다.

Fig. 9

Stress distribution near thrust disk and sensor components. (a), (c), (d) signed von Mises stress and (b) maximum principal stress (unit: MPa)

3.2.3 안전계수를 고려한 형상 개선 설계

쓰러스트 디스크 및 센서부 근처의 설계 변수 변화에 따른 경우 총 9가지 경우에 대하여 구조해석을 수행하여, 구성 부품에 대한 안전계수를 구하여 이들을 Table 3에 정리하였다. 안전계수는 최대응력을 극한응력으로 나누어 구하였다.

Table 3

Safety factors of components

Table 3에서 센서 마그넷의 안전계수가 작은 경우가 자주 발생하였다. 그 이유는 고속 회전에 의하여 발생하는 인장응력이 센서 마그넷의 작은 인장 극한응력 값(42 MPa)을 초과하는 경우가 자주 발생하였기 때문이다.

Table 3에서 경우 1~3은 센서 슬리브의 길이 L₁이 변화할 때 구성 부품에서의 안전계수이다(쓰러스트 디스크의 후방 길이 L₂ 및 센서 슬리브 압입량 S_in의 값은 초기 설계 상태에 해당하는 값으로 고정). 이들 각각의 경우에, 안전계수가 가장 낮은 부품은 센서 마그넷으로 나타났다. 각각의 경우 중에서, 센서 마그넷의 안전계수가 가장 높은 경우는 경우 3이다. 경우 3의 최소 안전계수는 0.67이다.

Table 3에서 경우 3~7은 쓰러스트 디스크의 후방 길이 L₂가 변화할 때 구성 부품에서의 안전계수이다(센서 슬리브의 길이 L₁ 및 센서 슬리브 압입량 S_in의 값은 초기 설계 상태에 해당하는 값으로 고정). 이들 각각의 경우에, 안전계수가 가장 낮은 부품은 센서 마그넷으로 나타났다. 각각의 경우 중에서, 센서 마그넷의 안전계수가 가장 높은 경우는 경우 7이다. 경우 7의 최소 안전계수는 1.09이다.

Table 3에서 경우 7~9는 센서 슬리브 압입량 S_in이 변화할 때 구성 부품에서의 안전계수이다(센서 슬리브의 길이 L₁ 및 쓰러스트 디스크의 후방 길이 L₂의 값은 초기 설계 상태에 해당하는 값으로 고정). 이들 각각의 경우에, 안전계수가 가장 낮은 부품은 센서 마그넷 또는 센서 슬리브로 나타났다. 각각의 경우 중에서, 최소 안전계수가 가장 높은 경우는 경우 8이다. 경우 8의 최소 안전계수는 센서 슬리브에서 나타났으며 그 크기는 2.04이다.

쓰러스트 디스크 및 센서부에서 세 개의 설계 변수(센서 슬리브의 길이 L₁, 쓰러스트 디스크의 후방 길이 L₂ 및 센서 슬리브 압입량 S_in)를 변화시킨 해석 결과로부터 경우 8 (L₁=10.7 mm, L₂=4.00 mm 및 S_in=0.02 mm)일 때, 각 구성 부품의 최소 안전계수가 가장 높은 크기를 갖는 최적의 경우로 나타났다.

4. 피로 수명 예측

ANSYS사의 상용 프로그램인 nCode Design Life 이용하여 공기압축기의 센서부에 대하여 피로해석을 진행하여 피로수명을 구하였다.¹²⁾

4.1 평균응력 보정

피로해석이론은 응력-수명 이론과 변형률-수명 이론으로 구분된다.¹³⁾ 응력-수명 이론은 재료에 작용하는 응력이 탄성영역 내에 있고, 그 결과로 피로수명이 긴 경우(High Cycle)에 적용되는 이론이다. 변형률-수명 이론은 탄성영역은 물론이고 소성영역까지 고려하며, 피로수명이 낮은 경우(Low Cycle)에 주로 사용되는 이론이다. 본 연구에서 구조해석 결과, 모든 경우에 최대응력이 재료의 항복강도보다 작기 때문에 탄성영역을 벗어나지 않는다. 따라서 응력-수명 이론을 적용하여 피로수명을 예측하였다.

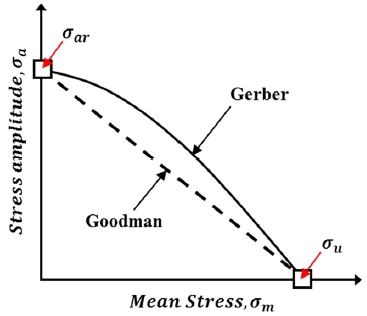
응력-수명 이론을 사용하여 피로수명을 예측할 때, 반복 하중에서 파괴까지의 반복수에 대한 관계로 나타난 응력-수명 선도(Stress-Life Curve)를 사용한다. S-N선도의 가로 축은 반복수(N)를 나타내고 세로 축은 반복 응력의 크기(σ_a)을 나타낸다. 일반적인 S-N선도는 평균응력의 크기(σ_m)이 0인 상태에서 작도된다. 만약 평균응력의 크기가 0이 아닌 경우에는, 이를 보정하는 방법이 필요하게 된다.¹³⁾ 평균응력을 보정하는 가장 일반적인 두 가지 방법은 Goodman과 Gerber에 의한 보정법이다(Fig. 10).

Fig. 10

Mean stress correction methods by Gerber and Goodman

Fig. 10에서 σ_ar는 평균응력의 크기가 0인 상태에서의 반복 응력의 크기이며 σ_u는 극한응력의 크기이다. Goodman은 σ_ar과 σ_u를 직선으로 연결하여 평균응력을 보정하였으며, Gerber는 σ_ar과 σ_u를 포물선으로 연결하여 평균응력을 보정하였다.¹³⁾

$\[ \begin{array}{c}\left.1\right) Goodman:\frac{{\sigma }_a}{{\sigma }_{ar}}+\frac{{\sigma }_m}{{\sigma }_u}=1\hfill \\ \left.2\right) Gerber:\frac{{\sigma }_a}{{\sigma }_{ar}}+{\left(\frac{{\sigma }_m}{{\sigma }_u}\right)}^2=1\hfill \end{array} \]$

4.2 개발 완료된 로터 어셈블리의 피로 시험 및 해석 결과

개발 완료된 최대속도 100 krpm의 로터 어셈블리에 대하여 피로 시험과 해석을 수행하였다. 정지와 최대속도로 가동을 반복적으로 수행하는 조건을 사용하였다.

개발 완료된 최대속도 100 krpm의 로터 어셈블리에 대한 피로 시험에서는 정지와 최대속도에서의 가동을 98,000사이클 반복하였을 때, 쓰러스트 디스크에서 파손이 발생하였다. 쓰러스트 디스크가 파손되어 분리된 로토 어셈블리와 파손된 쓰러스트 디스크의 사진을 Fig. 11에 나타내었다. 시험에서 파손이 발생한 부위와 유한요소해석에서 최대응력이 발생하는 부위는 일치하였다.

Fig. 11

Air compressor rotor and thrust disk which failed due to fatigue in 98,000 cycles

개발 완료된 최대속도 100 krpm인 로터 어셈블리의 쓰러스트 디스크에 대한 피로 해석에서는 평균응력을 보정하는 방법에 따라서 피로수명의 차이가 매우 크게 나타났다(Table 4). Gerber, Walker 또는 FKM에 의한 평균응력을 보정하는 방법을 사용하였을 경우, 피로 시험에서 얻은 피로수명 98,000사이클과 비교하여 최소 2.8배 이상의 피로수명을 해석으로 얻을 수 있었다. 실제 피로시험에서 얻은 피로수명과 가장 유사한 결과는 Goodman의 평균응력 보정 방법을 사용하였을 때이다(Table 4).

Table 4

Analysis and test results of fatigue life on existing air compressor rotor assembly

4.3 개발 중인 로터 어셈블리의 피로 수명 예측

이미 개발 완료된 로터 어셈블리의 피로수명 해석에서, Goodman의 평균응력 보정 방법을 사용하였을 경우에 가장 피로시험과 유사한 결과를 얻을 수 있었다(Table 4). 따라서 개발 중인 로터 어셈블리가 정지 상태와 최대속도 125 krpm으로 반복적으로 가동될 때 Goodman의 평균응력 보정 방법을 사용하여 피로해석을 수행하였다. 그 결과 각 주요 부품에서 얻은 피로수명을 Table 5에서 정리하였다.

Table 5

Analysis results of fatigue life on a new air compressor assembly under development

로터 어셈블리의 어느 부품이라도 파손되면 로터 어셈블리가 파손되는 것으로 간주해야 하므로, 개발 중인 로터 어셈블리의 피로수명은 238,000사이클이라고 예측할 수 있다. 이미 개발 완료된 로터 어셈블리의 피로수명은 88,300사이클에 불과하였다. 개발 중인 로터 어셈블리의 쓰러스트 디스크의 형상을 좌우 대칭에 가깝게 설계함으로써, 개발 완료된 로터 어셈블리에 비하여 피로수명을 크게 증가시킬 수 있었다.

5. 결 론

공기압축기 로터 어셈블리에서 임펠러 디스크의 후방 디스크 두께의 변화에 따라서, 임펠러에서 발생하는 응력과 변위가 영향을 받음을 확인하였다. 또한 응력과 변위가 최소화될 수 있는 최적의 후방 디스크 두께가 존재함을 확인하였다.

쓰러스트 디스크 및 센서부 근처의 설계변수 변화에 따라서 구성 부품들의 안전계수가 영향을 받음을 확인하였다. 안전계수가 가장 작은 구성 부품의 안전계수를 최대화하는 방법으로 가장 최적의 설계변수의 크기를 찾을 수 있었다.

이미 개발이 완료된 로터 어셈블리에서, Goodman의 평균응력 보정 방법을 사용하였을 때 피로 실험과 가장 유사한 해석 결과를 얻을 수 있었다. 따라서 개발 중인 로터 어셈블리에 대하여, Goodman의 평균응력을 보정하는 방법을 사용하여 피로수명을 예측할 수 있었다.

Acknowledgments

이 논문은 2018년도 한국기술교육대학교 교수 교육연구진흥과제 및 산업통상자원부와 한국산업기술진흥원의 “수소연료전지차 부품실용화 및 산업기반육성사업” (과제번호 R0006468)으로 수행된 연구결과입니다.

References

• M. S. Kim, and S. C. Kim, “BOP of Fuel Cell Vehicles”, Auto Journal, KSAE, 29(2), p30-35, (2007).
• Y. B. Lee, H. S. Lee, and J. T. Chung, “An Experimental Study on the Durability Test for PEM Fuel Cell Turbo-blower”, Transactions of KASE, 16(5), p37-43, (2008).
• K. K. Ha, S. M. Sung, S. H. Kang, H. R. Keon, and C. H. Lee, “Evaluations of the Turbo Blower Improvement Designs for the Fuelcell Vehicles”, KSME Annual Conference Proceedings, p458-461, (2008).
• J. Y. Yook, H. S. Yang, C. H. Lee, K. S. Cho, and K. I. Kim, “Dynamic Analysis of FCEV Turbo Blower”, The Korean Society for Noise and Vibration Engineering, 21(7), p591-598, (2011). [https://doi.org/10.5050/ksnve.2011.21.7.591]
• X. Zheng, L. Jin, Y. Zhang, H. Qian, and F. Liu, “Effects of Disk Geometry on Strength of a Centrifugal Compressor Impeller for a High Pressure Ratio Turbocharger”, Proceedings of Gas Turbine India Conference, p683-690, (2012). [https://doi.org/10.1115/gtindia2012-9690]
• H. S. Yang, D. B. Kwon, K. S. Cho, and C. H. Lee, “The Study of Noise Reduction FCEV Air Blower”, KSAE Annual Conference Proceedings, p2354-2358, (2012).
• H. S. Kang, and J. S. Han, “Shape Optimization of Blades for Centrifugal Compressor Impeller Using FSI Analysis and RSM”, KSME Annual Conference Proceedings, p324-329, (2013).
• S. Liu, C. Liu, Y. Hu, S. Gao, Y. Wang, and H. Zhang, “Fatigue Life Assessment of Centrifugal Compressor Impeller Based on FEA”, Engineering Failure Analysis, 60, p383-390, (2016). [https://doi.org/10.1016/j.engfailanal.2015.11.035]
• J. R. Davis, Concise Metals Engineering Data Book, ASM International, (1997).
• Ansys, Inc., https://www.ansys.com/ko-kr/products/platform/ansys-meshing (2018).
• Ansys, Inc., https://www.ansys.com/ko-kr/products/structures (2018).
• Ansys, Inc., https://www.ansys.com/ko-kr/products/structures/ansys-ncode-designlife (2018).
• N. E. Dowling, Mechanical Behavior of Materials, Pearson, Harlow, (1988).