2차원 평면 형태의 심층학습 기반 깊이 카메라 캘리브레이션

1. 서 론

컴퓨터 비전, 영상처리 분야에서 공장 자동화, 로봇과 같은 인간의 시각을 대체하거나 보조하는 기술에 대한 연구가 활발하게 진행되고 있다.¹⁾ 컴퓨터 비전, 영상처리 분야에서 공장 자동화, 로봇과 같은 인간의 시각을 대체하거나 보조하는 기술에 대한 연구가 활발하게 진행되고 있다.²⁾ 인간이 정보를 받아들이는 일을 하면서, 인간의 눈은 주변 정보를 이해하고 받아들이는 역할 중 70 % 이상을 기여한다. 컴퓨터 비전 분야의 목표는 인간 대신 기계가 장면 또는 물체를 인식하고 이해하는 일을 하도록 하는 것이다. 인간은 주변상황에 따라 시각을 통한 판단력이 항상 일관되지 않을 수 있다. 그러나 기계는 물리적 결함이 발생하지 않는 한, 판단의 일관성을 유지할 수 있다는 장점이 있다. 그리하여 결함 검출, 물체인식, 의료영상 등의 분야에서 컴퓨터 비전 및 영상처리 기술이 차지하는 비중이 점차 높아지고 있다.³⁾ 인간이 시각을 통해 장면을 인식할 때에는 장면 또는 물체의 3차원 정보를 기초로 하며 컴퓨터 비전 분야에서 3차원 좌표 정보를 획득 또는 복원하는 기술의 필요성은 점차 증가하고 있다. 카메라의 성능에 영향을 주는 환경적 요인을 정량적으로 나타내는 변수를 구하여 3차원 물체가 속한 좌표와 이것이 투영된 영상 평면에서의 2차원 좌표로 사이의 관계를 정립하는 절차, 그리고 카메라 내부 요인에 의한 영상 왜곡 등의 현상을 정량적으로 정의하는 절차를 카메라 캘리브레이션(Camera calibration)이라고 한다. 본 논문에서는 카메라 캘리브레이션 정확도를 개선하기 위한 방법을 제안한다. 특히 캘리브레이션을 수행하기 위해 필요한 절차인 코너 검출의 정확도를 높이기 위해 심층학습 개념을 적용한다. 지난 수십년간 가장 많이 사용되어온 캘리브레이션 알고리즘은 Zhang³⁾에 의해 개발되었으며, Zhang의 캘리브레이션에서 가장 중요한 절차 중 하나인 호모그래피 행렬(homography matrix) 도출 방법은 크게 네가지로 분류할 수 있다. 첫 번째 방법은 물체의 3차원 좌표와 2차원 좌표 간의 관계로부터 정의되는 호모그래피 행렬이고, 두 번째는 스테레오 카메라가 획득한 한 쌍의 2차원 물체들 간의 관계로부터 정의되는 호모그래피 행렬이다. 나머지 두 개는 직선 간의 기하학적 관계로부터 정의되는 호모그래피 행렬이며, 자세한 내용은 Zhang의 논문에 설명되어 있다.³⁾ 3차원 카메라 캘리브레이션 방식은 2개 혹은 3개의 직선들로 구성된 체커보드와같은 패턴을 사용하며 가장 정확도가 높은 방식이다. 2차원 평면 기반의 경우에는 2차원 평면에 나타난 물체의 이동을 관측해 캘리브레이션을 수행하고 1차원 직선 기반의 캘리브레이션은 고정된 점의 움직임을 이용해 캘리브레이션을 수행한다. 자가 캘리브레이션은 특정한 패턴물체를 사용하지 않고 한 물체에 대해서 여러 각도로 찍힌 여러 장의 이미지들을 사용해 캘리브레이션을 수행한다. 카메라 캘리브레이션은 체커보드와 같은 특정패턴을 가진 물체를 사용한 캘리브레션과 특정 물체를 사용하지 않은 캘리브레이션으로 나눌 수 있다. 전자는 전통적 캘리브레이션(Conventional calibration)이라고 하고, 후자는 자가 또는 자동 캘리브레이션(Self- or automatic calibration) 이라고 한다. 자가-캘리브레이션은 무인자동차와 로봇과 같은 분야에서 외부의 충격으로 카메라의 환경이 변경되는 경우를 대비해 실시간으로 카메라 캘리브레이션을 수행하는 것이며, 현재 연구가 활발하게 이루어지고 있다. 그리고 자가 캘리브레이션을 적용함으로서, 기존에 수십 번의 체커보드 촬영을 하는 비효율적인 절차를 줄일 수 있다. 또한, 많은 촬영으로부터 얻어진 영상을 활용한 캘리브레이션은 최적화 과정에서 과적합 등의 부작용이 발생할 수 있다. 소실점(Vanishing point)을 이용한 캘리브레이션은 스테레오 카메라로부터 찍힌 한 쌍의 영상에서 획득된 소실점을 기반으로 한 매칭을 통한 방법이다. 기존의 자가 캘리브레이션에서는 주로 기본 행렬(Fundamental matrix)을 활용하여, 획득된 영상들 간의 기하학적 제약사항을 활용하는 것이다.^4-7) 전통 방식의 캘리브레이션은 특정 패턴의 기구를 사용하는 제약이 있다. 하지만, 전통 방식의 캘리브레이션의 결과가 여전히 자가 캘리브레이션보다 높으며, 그 결과의 안정정이 뛰어나다는 장점이 있다.³⁾ 체커보드 패턴을 가진 물체와 함께 주기적 원형보드, 비주기적 원형보드를 사용하는 등 다양한 형태의 패턴을 이용해 캘리브레이션의 정확도 및 절차의 효율성을 높이기 위한 연구가 진행되었다.⁸⁾

본 논문에서는 전통 방식의 캘리브레이션에서 사용하는 체커보드 물체를 사용한 캘리브레이션을 수행한다. 기존의 방법과 다르게 체커보드 형태의 물체를 활용한 코너 검출 정확도를 향상시켜 캘리브레이션의 전체 정확도를 높인다. 특히 본 논문에서 가장 높은 기여를 하는 부분은, 코너 검출을 위해 심층학습 알고리즘을 적용하는 것이다. 그리고 심층학습 알고리즘을 적용함으로서 기존의 전통 캘리브레이션 방법이 사용한 수십 번의 영상촬영 횟수를 줄이는 것이다. 본 연구에서는 촬영횟수를 2회로 줄이면서 재투영 오류를 감소시켰다. 심층학습 알고리즘은 체커보드 형태의 물체를 검출하고, 그 물체에 속한 코너를 추출하는 절차에서 그 정확도를 높이는데 기여한다. 체커보드 물체 및 코너 검출에 필요한 신경망 알고리즘은 3개의 은닉계층을 거쳐서 각 은닉 계층마다 5단계의 세부 절차를 거친다. 그 5단계의 세부 절차는 Prepare, FAPL, PAMFG, Reconstruction, and PADCROP 이며 본론에서 자세히 다룬다.⁹⁾ 본 연구에서 제안한 방법을 통한 캘리브레이션의 결과는 재투영 오류(Re-projection error)를 활용하여 그 성능을 검증한다.

본 논문의 구성은 다음과 같다. 2장에서는 본 논문의 핵심내용인 심층학습 기반의 캘리브레이션 방법을 제안하고, 3장에서는 실험 결과를 통해 본 연구에서 제안한 방법의 성능을 제시한다. 그리고 4장에서 본 논문을 끝맺는다.

2. 본 론

이 장에서는 카메라 캘리브레이션 수행에 필요한 기하학적 변환 관계, 구성요소들 간의 상대적인 좌표 시스템에 대한 소개를 하고, 캘리브레이션의 방법 중 오랫동안 사용되어왔고, 대표적 방법 중 하나인 Zhang의 카메라 캘리브레이션 방법에 대해서 간략히 설명한다.

2.1 카메라 캘리브레이션

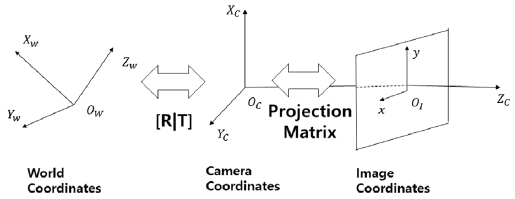
카메라 캘리브레이션은 3차원 공간상의 점들(또는 영역)이 2차원 이미지 평면에 투영될 때 카메라의 내, 외부환경으로 인해 발생하는 기하학적인 요인에 대한 파라미터를 구하는 것이다. 카메라의 내부 요인 또는 내부 특성을 정의하는 요소들로 구성된 파라미터들을 내부 파라미터(Intrinsic parameters), 특성을 정의하는 요소들로 구성된 파라미터들을 외부 파라미터(Extrinsic parameter)라고 한다. 외부 파라미터는 현실 3차원 좌표계와 비교하여 카메라의 상대적인 위치를 나타내고, 회전(R) 및 변위(T) 행렬로 표현될 수 있다. 그리고 내부 파라미터는 투영 행렬(Projection matrix)의 성분으로 표현될 수 있다(Fig. 1 참조). 내부 파라미터는 A, 외부 파라미터는 [R|T]로 표기한다. 3차원 좌표와 2차원 좌표 간의 관계는 식 (1)처럼 표현될 수 있다.³⁾

Fig. 1

Relationship between world, camera and image coordinate systems

$\[ s\left(\begin{array}{c}x\\ y\\ 1\end{array}\right)=\mathrm{A}\left[\mathrm{R}|\mathrm{T}\right]\left(\begin{array}{c}{\mathrm{X}}_{\mathrm{W}}\\ {\mathrm{Y}}_{\mathrm{W}}\\ {\mathrm{Z}}_{\mathrm{W}}\\ 1\end{array}\right) \]$

(1)

s는 상수이며 스케일(Scaling factor) 표현을 위한 것이다.

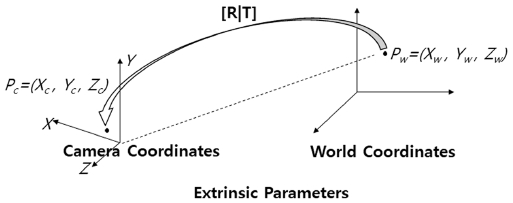
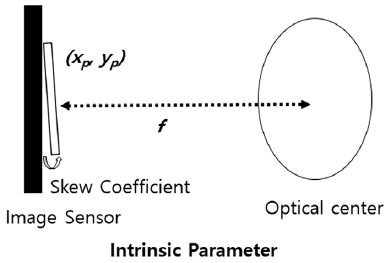
내부파라미터(Intrinsic Parameter)는 초점거리(Focal length, f), 비대칭 계수(Skew coefficient), 중심점(Principal point, ((x_p,y_p)) 로 이루어진다. 내부 파라미터를 구성하는 행렬 A (식 (1))에서 비대칭 계수는 0으로 고정시키기도 한다. 초점거리는 카메라 렌즈(광학 중심)와 이미지 센서간의 거리, 중심점은 렌즈의 중심에서 이미지 센서로 사영(Projection)된 곳에 위치한다. 그리고 비대칭 계수는 이미지 센서의 수직축(y축)이 기울어진 정도를 나타낸다. 기울어짐이 없는 경우는 비대칭 계수는 0이다. 외부파라미터 계산을 위한 요소로 회전과 변이로 표현된다. 한 개의 카메라를 사용할 경우 회전은 3차원 현실 좌표계와 카메라가 속한 좌표계사이의 회전각을 나타내고, 스테레오 카메라를 사용할 경우에는 사용된 카메라들 간의 상대적 회전각을 나타낸다. 그리고, 스테레오 카메라에서 변위 값은 두 카메라의 광학 중심간의 거리로 표현될 수 있다. 그러므로, 외부 파라미터는 카메라와 현실 좌표계 간의 상대적인 위치를 나타내고, 이것은 3차원 물체 또는 장면의 상대적 원근을 표현하기에 적합하다. 절대적인 원근값을 구하기 위해서는 추가로 내부 파라미터가 필요하고, 이것은 식 (2)를 통해 표현할 수 있다.

$\[ z=\frac{bf}{d} \]$

(2)

z는 3차원 물체 중 목표가 되는 점과 카메라 사이의 거리이고, b,f,d는 두 카메라 사이의 거리, 초점거리, 디스패리티(Disparity)를 각각 나타낸다. 카메라 캘리브레이션 절차에서 필요한 좌표간의 변환관계를 이해하기 위해서는 Fig. 1, Fig. 2, Fig. 3에서 나타난 좌표계들에 대한 이해 및 계산이 필요하다. 여러 대의 카메라를 사용하는 깊이 카메라 시스템에서는 서로 다른 초점거리(또는 동일 카메라의 경우에도 초점 거리는 다를 수 있으므로) 에 대한 문제점을 해결하기 위해 정규화된 좌표(Normalized coordinate)를 사용할 수 있다.¹⁰⁾ 현실 좌표계(World coordinate)는 3차원 사물의 위치를 표현할 때 사용하는 좌표계이고 카메라 좌표계(Camera coordinate)는 카메라가 속한 3차원 공간을 표현할 때 사용하는 좌표계이다. 현실 좌표계에서 카메라 좌표계로 변환된 후 2차원 영상 좌표계로 투영될 때 픽셀 좌표계로 표현하기 전에 사용하는 실제 이미지의 좌표계를 필름 좌표계(Film coordinate)라고 한다.¹¹⁾ 영상처리에서는 영상의 픽셀단위 조작을 위해 필름 좌표계를 픽셀 좌표계로 이산화 시킨다.

Fig. 2

Extrinsic parameters of a camera and relationship between coordinate systems

Fig. 3

Intrinsic parameters of a camera

2.2 카메라 캘리브레이션

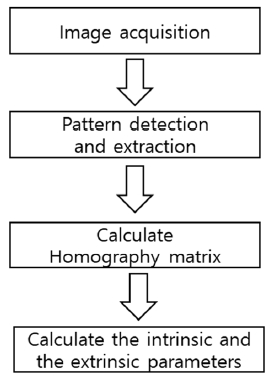
Fig. 4는 전통적으로 많이 사용되어 온 카메라 캘리브레이션의 절차를 보여주고 있다. 대표적인 전통 방식의 카메라 캘리브레이션은 ^3,8,12,13)에서 자세히 설명되어 있고, 캘리브레이션 알고리즘의 이해를 돕기위한 대표적인 방식이며 현재까지도 많이 활용되고 있다. 지금까지는 2000년에 발표된 Zhang의 논문에 기반한 방식이 가장 많이 사용되고 있고, 정확도 및 안정성이 높은 방식이다. 호모그라피 행렬을 추정(Fig. 4 참조)하는 기본 행렬(Fundamental maxtirx 또는 Essential matrix)의 절차는 본 논문에서 다루는 주된 내용은 아니므로, 자세한 설명은 생략한다. 호모그래피 행렬은 식 (3)에서 3×3행렬로 표현된다.

Fig. 4

Camera calibration (Conventional approach)

$\[ \left(\begin{array}{c}x\\ y\\ w\end{array}\right)=\left(\begin{array}{ccc}{H}_{11}& H_{12}& H_{13}\\ H_{21}& H_{22}& H_{23}\\ H_{31}& H_{33}& H_{33}\end{array}\right)\left(\begin{array}{c}X\\ Y\\ Z\end{array}\right) \]$

(3)

w는 2차원 좌표의 균질좌표계(Homogeneous)로 표현하기 위해 사용된 상수이며, 1로 고정하여 사용할 수 있다. 최종적으로 비선형 최적화(Nonlinear optimization)를 거친 후 계산된 파라미터들을 활용하여 재투영 오류를 계산하고 카메라 캘리브레이션의 정확도를 평가한다. 재투영 오류란 3차원 포인트들을 2차원 평면으로 재투영했을 때, 영상에서 얻어진 포인트들과 재투영된 포인트들의 간의 차이로 정의된다. 카메라 캘리브레이션의 정확도를 평가하는 방법은 여러 가지가 있을 수 있으나, 일반적으로 활용되는 평가 기준은 재투영 오류(Re-projection error)이다. 이에 본 논문은 코너 검출의 효율 및 정확도를 높여 캘리브레이션의 정확도를 높이기 위해 심층학습 기술을 적용한다. 심층학습 알고리즘은 체커보드의 형태를 검출하고, 그 안에 속한 코너 및 에지(Edge)를 추출하여 결과적으로 호모그래피 행렬의 안정적인 계산 및 전체 캘리브레이션의 정확도를 높인다. 여기서 정확도는 재투영 오류로 정의한다.

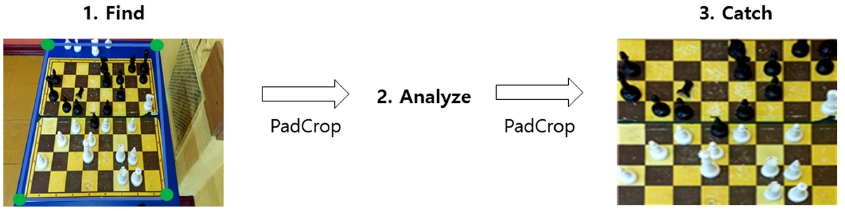
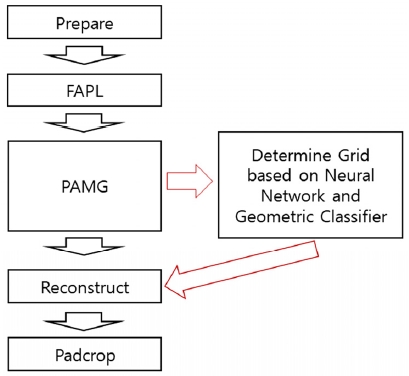
체스보드 검출을 위해서 입력된 영상에서 주변 배경 및 잡음을 제외한 체스보드 검출 과정이 진행된다(Fig. 5). Fig. 5에서 영상을 찾는(Find) 과정 완료 후 Fig. 6의 단계가 수행되고, 체스보드 영상을 찾은 후 기하학적 변환을 하기 직전에도 Fig. 6의 단계가 수행된다. 이 과정에서 체스보드 탐지와 추출하는 정확도를 높이기 위해 에지 및 코너 검출을 학습 기반으로 수행한다. 그리고 학습 단계에서 3개의 은닉 계층이 존재하며, 각 계층마다 Prepare, FAPL, PAMG, Reconstruct 그리고 Padcrop의 총 5단계의 절차가 진행된다. Prepare는 체커보드의 선을 찾기위한 사전작업이다. Retinex 알고리즘¹⁴⁾을 활용해 입력된 영상에서 불필요한 배경성분을 제거해 체커보드의 위치를 대략적으로 찾아 추출한다. FAPL은 Retinex 알고리즘을 통해 처리된 영상에서 선 영역을 찾아내는 과정이다. Over-exposed, Blurred 그리고 Tinted 등의 효과를 적용하여 최종적으로 선 모양으로 판단되는 영역을 모두 나타냄으로서 선을 검출한다. PAMG는 체스보드의 Padcrop을 위한 코너검출 과정이고, Padcrop은 각 은닉계층의 마지막 단계에서 영상을 획득하는 과정이다.

Fig. 5

Learning based detection of a chessboard

Fig. 6

Corner and edge detection from chessboard image

PAMG 단계에서는 학습기반의 신경망(Neural network) 알고리즘과 비학습 기반 방식인 기하학적 분류기(Geometric classifier)를 함께 사용하여 추출의 정확도를 높인다. 체스보드의 격자 코너를 정확하기 추출하기 위한 방법으로 기하학적 분류기를 사용하여 격자 형태가 완벽한 경우만을 인식하고 신경망 알고리즘은 영상의 왜곡에 상관없이 격자의 형태를 학습기반으로 추출한다. 최종적으로 PAMG 단계에서는 기하학적 분류기를 통한 검출 성공, 신경망 알고리즘을 통한 검출 성공, 그리고 검출 실패의 경우이다. Reconstruct 단계에서는 PAMG에서 검출된 코너들로 격자(Grid)의 형태를 변환시킨다(Fig. 5 우측 참조). Grid 계산방법으로는 그리드 밀도 공식을 사용한다((식 (4) 참조).

$\[ S=\frac{p^3}{nlo{g}_{10}\left(n\right)} \]$

(4)

p는 프레임 내부의 코너의 개수, n는 표면적을, S는 밀도를 의미한다. 코너 및 에지 추출 과정에서 계산된 밀도 값 중 가장 큰 값을 선택한다. Padcrop 단계는 Padding과 Crop을 합친 것이며, 각 은닉계층 단계에서의 계산이 종료될 때마다 영상을 Crop하여 Fig. 5의 우측 영상처럼 변환한다. 카메라 캘리브레이션의 코너검출 정확도를 높이기 위해 Fig. 6에서 설명한 5개의 단계를 은닉계층의 개수만큼 거쳐서 체커보드를 추출한다. 본 연구에서 은닉계층의 수는 3이다. 다음 장에서는 본 연구에서 제안한 방법을 실제 캘리브레이션 절차에 적용하여 그 결과를 제시한다.

3. 실 험

체스보드 검출을 위해 신경망 알고리즘을 적용한다. 학습(Training) 데이터는 총 9,664개이며 학습 데이터는 Fig. 7과 같다. 격자가 존재하는 경우(Train_ok, 4,732개)와 그렇지 않은 경우(Train_no, 4,932개)를 분류하여 왜곡된 부분의 체스보드 격자를 판별하도록 학습시킨다.

Fig. 7

Training data of existence of grid(Train_ok) and nonexistence of grid(Train_no)

Table 1

Size of images and number of corners used in experiments

지정한 알고리즘 수행 횟수만큼 학습을 마치면 Fig. 7과 같이 Test 샘플을 통해 Fig. 8처럼 체커보드를 추출할 수 있다. 수행횟수의 지정은 수동으로 임의로 지정하였으며 본 연구에서는 50회에서 1000회까지 증가시키며 그 결과를 분석하였다. Table 2에 제시된 것처럼, 본 논문에서 적용한 심층학습 방법은 전체적인 캘리브레이션의 성능(재투영 오류 기반)을 개선시켰다. 다만, 본 논문에서 사용한 영상에서 코너 추출의 성능이 어느정도 확보되었을 경우 재투영 오류의 감소는 크지 않았으나, 기존의 방법³⁾ 대비 감소를 보였다.

Fig. 8

Example results of chessboard detection and corner extraction

Table 2

Comparision results

본 연구에서 제안한 방법과 Zhang의 방법과의 재투영 오류 비교 결과는 Table 2에 제시하였다.

Table 2에서 제시되었듯이, 학습기반으로 코너추출을 한 후 캘리브레이션을 수행할 경우, 재투영 오류가 기존의 방법 대비 감소하였음을 확인할 수 있다. 기존의 방법처럼 여러 장의 영상을 다른 위치에서 찍으며 캘리브레이션을 수행하는 것보다, 학습기반의 코너추출을 적용하여 적은 수의 영상을 촬영한 후 캘리브레이션을 하는 효율적인 캘리브레이션을 수행할 수 있다. 학습기반 알고리즘을 적용한 경우 Table 1처럼 기존에 입력된 이미지의 해상도보다 낮은 해상도로 변환되지만 Table 2처럼 작업 량도 비례하여 줄어들기 때문에 수행속도가 증가하였다. 마지막으로 Table 3에서 제시된 것처럼 학습 수행 횟수를 늘렸을 경우 체커보드 추출에대한 정확도가 증가된 것을 확인할 수 있다. Table 3에서 제시된 정확도는 체스보드 검출 정확도를 의미하는 것이고, 참 양성 비율(True positive) 값으로 Table 값이 구현된다.

Table 3

Accuracy(true positive) of training data with a number of iterations

4. 결 론

본 논문은 카메라 캘리브레이션의 정확도를 높이기위해 카메라 캘리브레이션의 과정 중 코너 검출 부분에서의 정확도를 높이고, 3차원의 실제 영상과 투영된 2차원 영상 간의 호모그래피 행렬 계산의 정확도를 높이기 위해 심층학습 기반 알고리즘을 적용하였다. 인공 신경망은 3개의 은닉계층으로 이루어져 있으며 각 계층마다 5개의 단계를 거쳐 캘리브레이션에 필요한 체스보드 영상을 생성하며 이를 이용하여 코너를 추출할 경우 기존의 캘리브레이션 방법 대비 재투영 오류가 감소하였음을 확인하였다. 그리고 인공신경망은 각 계층에서의 5단계 중에서 PAMG 단계에 학습기반 알고리즘을 적용한다. Table 3에서 제시된 것처럼 학습 횟수를 50회부터 시작하여 1000회까지 증가시키면서 체커보드 추출에 대한 정확도가 증가하였지만 호모그래피 행렬 계산은 동일하기 때문에 학습기반 알고리즘으로 추출된 체커보드에 대한 재투영오류는 학습횟수가 증가하더라도 큰 변화가 없음을 확인할 수 있다. 그 이유는 본 논문에서 사용된 입력 영상의 품질은 어느정도 일관되기 때문이다. 입력 영상의 화질이 낮을수록, 학습을 통한 재투영오류 결과의 개선은 더욱 뚜렷할 것이다. 본 연구에서 제안하는 학습 기반 방법을 적용할 경우, 특수 실험환경이 아니더라도, 코너추출 단계에서 체커보드 외에 불필요한 영상들을 모두 제외시키는 전 처리과정이 있기 때문에 일반적인 환경에서도 높은 정확도를 가지는 캘리브레이션을 수행할 수 있다. 제안된 방법을 통해 얻어진 코너 추출 결과는 호모그래피 행렬의 정확도를 높일 수 있다. 다만, 본 논문에서는 호모그래피 행렬 계산 전까지의 단계만 다루었으며 향후 연구에서 심층학습 알고리즘을 통해 호모그래피 행렬 계산 결과가 카메라 캘리브레이션의 재투영 오류에 영향을 끼치는 과정을 연구할 계획이다.

Acknowledgments

본 연구는 2018년도 계명대학교 연구기금으로 이루어졌음.

References

• K. -S. Yang, J. -H. Park, C. -M. Jung, M. -W. Suh, and S. -H. Hwang, “Development of Real-Time Electric Vehicle Driving Simulator for the Verification of Vision Algorithm”, KSAE Annual Conference Proceedings, p2274-2278, (2012).
• K. Park, D. Lee, and Y. Park, “Hand Gesture Recognition Using Depth Information and Visual Image”, Journal of KIIT, 11(7), p57-65, (2013). [https://doi.org/10.14801/kiitr.2013.11.7.57]
• Z. Zhang, “A Flexible New Technique for Camera Calibration”, IEEE Transactions on Pattern Analysis and Machine Intelligence, 22, p1330-1334, (2000). [https://doi.org/10.1109/34.888718]
• S. -Y. Kim, and J. -H. Han, “A Constrained Self-Calibration Technique”, Journal of KISS : Software and Applications, 28(4), p358-368, (2001).
• B. Zhao, and Z. Hu, “Camera Self-calibration from Translation by Referring to a Known Camera”, Applied Optics, 54(25), p7789-7798, (2015). [https://doi.org/10.1364/ao.54.007789]
• S. Duan, H. Zang, M. Xu, X. Zhang, Q. Gong, Y. Tian, E. Liang, and X. Liu, “Camera Self-calibration Method based on Two Vanishing Points”, Proceedings SPIE 9675, AOPC 2015: Image Processing and Analysis, (2015).
• Q. -T. Luong, and O. D. Faugeras, “Self-Calibration of a Moving Camera from Point Correspondences and Fundamental Matrices”, International Journal of Computer Vision, 22(3), p261-289, (1997).
• J. Heikkila, “Geometric Camera Calibration using Circular Control Points”, IEEE Transactions on Pattern Analysis and Machine Intelligence, 22(10), p1066-1077, (2000). [https://doi.org/10.1109/34.879788]
• M. A. Czyzewski, A. Laskowski, and S. Wasik, “An Extremely Efficient Chess-board Detection for Non-trivial Photos”, arXiv:1708.03898v1.
• D. Kim, OpenCV Computer Vision Programming, Int Edn., Kame Publishing, Seoul, (2014).
• M. Garcia-Elias, K. -N. An, L. Berglund, R. Linsheid, W. Cooney, and E. Chao, “Extensor Mechanism of the Fingers. I. A Quantitative Geometric Study”, The Journal of Hand Surgery, 16(6), p1130-1136, (1991). [https://doi.org/10.1016/s0363-5023(10)80079-6]
• R. Tsai, “A Versatile Camera Calibration Technique for High-accuracy 3D Machine Vision Metrology Using Off-the-shelf TV Cameras and Lenses”, IEEE Journal on Robotics and Automation, 3(4), p323-344, (1987). [https://doi.org/10.1109/jra.1987.1087109]
• T. Kim, and T. Park, “Calibration Method between Two 3D LIDARs for Autonomous Vehicle”, KSAE Fall Conference Proceedings, p827, (2016).
• E. Provenzi, L. Carli, A. Rizzi, and D. Marini, “Mathematical Definition and Analysis of the Retinex Algorithm”, Journal of the Optical Society of America A, 22(12), p2613-2621, (2005). [https://doi.org/10.1364/josaa.22.002613]
• J. Leiner Barba, Q. Lorena Vargas, M. Cesar Torres, and V. Lorenzo Mattos, “Three-Dimensional Reconstruction Optical System Using Shadows Triangulation”, AIP Conference Proceedings, 992(1), p1073-1077, (2008).