점진적 L2-노름 기반 방법을 적용한 얼굴영상 분류 및 인식
Copyright Ⓒ 2019 KSAE / 162-01
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
This paper proposes an approach to face recognition by using the L2-norm method, and suggests an algorithm to solve the overdetermined system problem, which is one of the practical issues. The proposed approach is fully utilized, and it consists of incremental QR decomposition and block-wise matrix inversion. In this paper, L2-norm based algorithm is applied to a face recognition problem and the experimental results are used to verify the proposed method that provides competitive results compared to the existing methods(e.g., batch L2-norm based method). In addition, the proposed algorithm shows computational efficiency in that the training time is significantly reduced even if a new training data is added. A reduction of computational complexity is also verified by showing the experimental results.
Keywords:
Face recognition, Incremental L2-norm, Incremental QR decomposition, Blockwise matrix inversion키워드:
얼굴인식, 점진적 L2-노름, 점진적 QR 행렬분해, 블록 행렬 도치1. 서 론
지난 수 십 년간 얼굴 인식 기술은 연구 및 다양한 산업 분야에서 많은 관심을 받아왔다. 또한 얼굴인식 분야는 과거부터 학습을 통한 분류 알고리즘 기반으로 연구가 수행되었으며, 최근의 심층학습 기반 인식 연구의 기반 기술이라고 할 수 있다.1) 학습기반 얼굴인식의 목적은 학습된 얼굴 영상들을 활용하여 얼굴 인식률을 높이는 것이다. 과거의 많은 연구들은 수학적 모델에 기반한 얼굴 특징 표현(특징점)이나 특징을 활용한 매칭 또는 분류에 기반한 것들이었다. Eigenface,2) Fisherface,3) Laplacianface4) 등은 얼굴인식 분야 연구에서 초기에 제안된 알고리즘들이었으며, 이 연구들의 특징은 고차원에서 표현되는 영상신호들을 저차원에서 표현하는 방법을 찾는 것에 초점을 맞추었다. 그에 반해 최근접 이웃 분류기(Nearest Neighborhood Classifier),5) SVM(Support Vector Machine),6) 신경망(Neural Network)7) 알고리즘 등은 초기에 활발히 연구되었던 학습 기반의 얼굴 인식 알고리즘들이다. 앞에서 언급한 저차원 벡터를 활용한 얼굴인식 알고리즘은 특징점들의 집합을 저차원 공간으로 변환하는 것에 목적이 있었기 때문에 기저벡터를 최신화 하는 것이 중요한 요소였다. 기저벡터의 최신화를 위해서는 추가되는 학습 데이터를 포함한 모든 입력 데이터들의 특징점(또는 특징 벡터)들을 재학습(또는 재훈련)시켜야 하고 이러한 재학습의 절차는 시스템의 전반적인 계산효율에 큰 문제를 가져올 수 있다는 단점이 있다. 그리하여 특징점 추출 기반의 분류 및 인식 알고리즘 대비 희소 표현을 통한 분류 알고리즘에 대한 연구가 더 활발해지기 시작하였다. Wright 등8)은 선형회귀(Linear regression) 모델을 활용한 희소행렬(Sparse matrix, 또는 스파스행렬) 표현(Sparse representation)에 기반한 새로운 방식의 접근법을 소개하였다. 이 접근법에서 평가 데이터(Test data)는 학습데이터(Training data)의 선형 합으로 표현되고, L1-노름(Norm) 최소화 기법을 통한 희소 저차원(Sparse low-dimensional) 특징벡터 해를 얻게 된다. 희소 행렬(또는 벡터) 계수(Elements of sparse matrix)가 추출되면 평가(Test) 데이터는 그 계수들과 각 클래스의 학습 데이터를 활용한 근사치로 표현될 수 있다. 평가 데이터의 소속 클래스는 최소 잔차(Residual) 알고리즘을 통해 결정된다.9) Wright의 연구8)에서 제안한 알고리즘은 L1-노름 최소화를 통한 희소행렬에 기반한 영상 표현이 얼굴인식의 높은 인식률을 보여주는 것을 제시하고 있다. 그러나 희소행렬 표현을 통한 얼굴인식은 여전히 명확한 분석적 모델링을 제시하기에 한계를 보이고 있고, L1-노름 최소화는 여전히 높은 계산량이 필요하다는 단점이 있다. 그리하여 최근 몇 년간 진행된 얼굴인식 연구들은 L2-노름 기반 선형회귀 모델이 L1-노름 기반 알고리즘 대비 인식률에서 더 강인하고 알고리즘 계산량의 효율성에서 더 우세하다는 것을 제시하였다. 또한 행렬로 표현되는 영상의 희소성(Sparsity)에 대한 가정이 더 이상 유효하지 않을 경우 L1-노름 기반 압축센싱(Compressive sensing or compressed sensing) 방식보다 L2-노름 기반 방식의 알고리즘이 더 강인하고 정확도 높은 결과를 보인다는 연구결과도 제시되었다.10) 희소 표현(Sparse representation)을 통한 영상 분류 방법을 적용하여 얼굴인식에 적용하는 기술은 지금까지 활발히 연구되어 왔다. 새로운 입력 데이터를 축적된 학습 데이터의 선형 합(Linear combination)으로 간단히 표현하고, 분류의 오류를 최소화 하는 수학적 모델을 제시한 연구가11)에 제시되어 있으며, 이 연구에서도 협동 표현(Collaborative representation) 기반 분류 알고리즘을 제시하여 L1-노름 대비 결과의 우세함을 보여주고 있다.
본 논문에서는 점증적 L2-노름 기반 얼굴인식 방법을 제안한다. 기존에 Shi 등10)이 제안한 방법에서 점진적 학습 알고리즘을 추가한 방법을 활용한다. 제안하는 알고리즘은 기존의 방법처럼 고차원 영역에서 정의되고 표현되는 영상 데이터를 저차원으로 사영(Projection)하여 표현한 후 분류하는 분류기(Classifier) 제안 알고리즘이 아니며, 압축 센싱 처럼 신호의 희소성을 가정하지 않고 점진적(Incremental) 학습을 적용한 알고리즘이다. 본 논문에서는 얼굴인식 및 분류에서 발생할 수 있는 과적합 문제(Over-determined system problem)도 함께 다룬다. 또한 본 연구는 L2-노름 기반 학습결과가 점진적 QR 분해법과 블록 행렬 도치(Inversion)를 통해 점진적으로 최신화됨을 보인다. 특히, 본 논문에서 제시한 방법은 새로운 평가 데이터가 추가되더라도 학습에 소요되는 계산량(또는 계산시간)이 줄어드는 효과를 보인다. 계산량의 감소에도 불구하고 얼굴인식률은 기존의 배치(Batch) L2-노름 기반 방법을 적용한 결과와 유사함을 실험적으로 보인다. 본 논문의 구성은 다음과 같다. 2장에서는 L2-노름 기반 얼굴인식 방법의 수학적 모델을 제시하고, 3장에서 본 논문이 제시한 방법을 통해 QR 분해(Decomposition)와 블록행렬 도치화를 통한 최적화 해법을 제시한다. 본 논문에서 제시한 방법을 검증하기 위해 4장에서 실험결과를 제시하고 5장에서 본 논문을 끝맺는다.
2. L2 - Norm 기반 얼굴인식
벡터 v(v= [v1, v2, v3,......., vn-1,vn]T) (T: transpose)의 L2-노름 (L2-Norm) 는 식 (1) 과 같이 표현된다.
| (1) |
학습에 사용되기 위한 얼굴영상 데이터의 집합을 로 정의하고 X={x1,..........xn}로 표현한다. X의 각 요소인 xi(i=1,2,......,n-1,n)는 d 차원의 학습 얼굴영상이고 n은 X를 구성하는 얼굴 영상의 개수이다. xi는 l개의 클래스 중 하나에 속해 있다(즉, xi는 클래스 Ck, (k=1,2,...,l-1,l) 에 속해 있다). 얼굴인식의 기본적인 목표는 새로운 입력 영상 y가 입력으로 들어올 경우, y∈Ck를 만족시키는 k를 찾는 것이다. 즉 성공적인 분류는 인식률에 직접적인 영향을 준다. 새로운 입력영상(평가 데이터) 가 추가되면 y=Xα이 성립된다. 은 계수 벡터이다. 최소 복원 오류 결과 기반 최적의 α값은 식 (2)로부터 얻을 수 있다.
| (2) |
∥∙∥2 은 L2 노름을 나타낸다. 대부분의 얼굴인식 문제는 과결정(Over-determined) 문제인 경우가 많다 (d≫n). 그리고 최소자승법(Minimum least square method)에 의한 식 (2)에서의 α은 식 (3)에 의해 얻어질 수 있다.
| (3) |
Shi 등10)에 의하면 식 (2)에서의 α는 QR 분해(Decomposition)(X = QR)를 이용하여 효과적으로 계산될 수 있다.
| (4) |
R-1QT는 y와 서로 독립이고, α는 y를 R-1QT로 사영(Projection) 시킴으로서 구해질 수 있다. 학습 데이터의 수가 증가하면 X의 사이즈가 증가하므로 그에 따라 R-1QT의 계산량도 증가하며 이 현상은 전체적인 시스템의 계산 복잡도를 증가시키는 문제점이 될 수 있다. 정규화 식(Regularization term)을 추가한 L2 노름 방법을 활용하여 α는 식 (5)와 같이 계산될 수 있다.
| (5) |
λ는 정규화 계수이다. 정규화 부분식을 추가함으로써 L2-노름 방법을 이용하여 구해진 결과는 더 안정적이고 α가 희소성질(Sparsity)을 갖도록 해준다.11) 식 (5)로부터 α는 식 (6)과 같이 구해질 수 있다.
| (6) |
새로운 평가 이미지 y가 추가되면 y를 R-1QT 또는 (XTX+αI)-1XT에 사영시킴으로서 α를 구할 수 있다. 그러나 평가 이미지 y의 개수가 증가할수록 평가이미지가 학습 데이터에 추가되기 때문에 R-1QT 또는 (XTX+αI)-1XT 의 계산량은 크게 증가한다는 문제점이 있다. α가 계산되면 영상들이 소속된 모든 클래스들에서 계산되는 잔차(Residual)들을 y에 관한 함수로 표현할 수 있다. k 번째 클래스 Ck 에서의 잔차는 식 (7)과 같이 표현된다.
| (7) |
k=1,.......l이고 는 α의 부분 벡터이며 는 X의 부분집합이다. 본 논문에서는 이러한 한계점들을 해결할 수 있는 알고리즘을 제안하고자 하며, L2-노름 기반 방법을 활용한 최적 해법을 다음 장에서 설명하고 제시한다.
3. L2 - Norm 기반 최적 해법
본 연구에서 제안하는 점진적 방법은 점진적 QR 행렬분해와 블록행렬 도치(Block-wise matrix inversion)를 활용한 방법이다. 영상 집합 는 QR분해를 적용하여 QARA로 표현될 수 있다. 즉 XA=QARA이다. 새로운 영상 데이터셋 가 주어졌을 때 XB는 식 (8)과 같이 표현될 수 있다.
| (8) |
는 QA에 직교(Orthogonal) 성질을 가진 기저벡터로 구성된 행렬이다. 는 를 QR 분해하여 얻을 수 있다. 그리고 결합행렬 XC=[XA XB]는 QR 분해에 의해 XC=QCRC 로 표현될 수 있다. 점증적 학습에서 XA는 학습 전 과정에서 계산되고, 를 계산하는 과정에서의 계산량은 줄어든다. 즉, nA≫nB이다. 그러므로 새로운 학습데이터 XB가 추가될 경우 QC와 RC 의 업데이트는 비교적 짧은 시간에 이루어진다. 한편, 식 (5)는 식 (9)와 같이 표현될 수 있다.
| (9) |
그리고 이고, 은 대각행렬이며 대각성분은 이다. 식 (9)는 결국 식 (2)와 같은 형태이며, 점진적 QR 분해는 여전히 적용 가능함을 보이고 있다. 식 (2)을 활용할 경우 식 (9)에서의 α의 최적 해는 α=R-1QTy이고, 새로운 학습데이터가 추가될 때마다 R-1이 업데이트 될 필요가 있다. 업데이트는 블록 행렬 도치를 통해 얻을 수 있고, 블록행렬 도치의 식은 식 (10)처럼 표현할 수 있다.
| (10) |
A,B,C,D는 각각 블록 행렬(Sub-blocks of a matrix or sub-block matrix)을 나타내고, S=D-CA-1B는 행렬 A의 슈어 요소 (Schur component)12)를 나타낸다. 식 (10)은 A와 D가 정방(Square) 행렬이고, A와 S가 가역(Invertible) 행렬일 때 성립된다. 식 (11)에서는 블록 도치 행렬을 활용하여 의 업데이트 과정을 보여준다. RC의 역행렬은 식 (11)과 같이 표현된다.
| (11) |
그리고 이다. 식 (11)에서 표현된 것처럼 은 와 을 활용하여 계산될 수 있다. 특히, 은 미리 주어진 값이고, 는 RA에 비해 사이즈가 훨씬 작다. 그러므로 α=R-1QTy는 점진적 학습 절차에서 효율적으로 업데이트 될 수 있다. 위의 과정들(식 (8) ~ (11))을 모두 고려하였을 때, 새로운 평가 영상이 입력으로 들어오면 식 (7)을 활용하여 영상의 특징을 파악하고 소속 클래스를 결정하여 분류를 수행할 수 있다.
4. 실 험
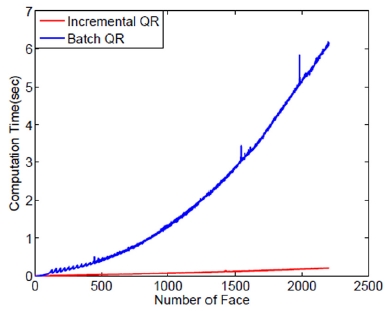
이 장에서는 본 논문에서 제안한 점증적 L2-노름 방법 기반 얼굴인식 성능을 실험적으로 보인다. 공개적으로 제공된 얼굴 데이터베이스들인 Yale B 와 AR face을 사용하여 실험을 진행하였다.13,14) Yale B 데이터베이스에서는 38명의 2,414개의 정면 응시 얼굴들을 사용하였다. 이 데이터베이스에서는 영상을 임의로 나누어 절반(1,207개)은 학습데이터, 나머지 절반(1,207개)은 평가데이터로 활용하였다. AR face 데이터베이스에서는 126명의 4,000개 이상의 정면응시 얼굴 영상을 실험에 활용하였다. 이 데이터베이스에서는 조명과 표정의 변화를 가지고 있는 50명의 남성과 50명의 여성의 얼굴 데이터를 선택하여 실험에 활용하였다. 각 사람마다 7개의 얼굴 영상이 학습용(총 350개)으로 선택되고 나머지 7개의 영상은 평가용(총 350개)으로 선택되었다. Yale B 및 AR face 데이터베이스 모두 그레이스케일(Grey-scale) 60×43 사이즈로 변환하여 실험에 사용하였다. 잔차 부분식(Residual term)을 활용하기 위해, 영상 데이터들은 단위(Normalized) L2-노름을 가지도록 정규화(Normalization)하였고, 식 (10)의 는 계산의 편이성을 위하여 0.1로 설정하였다. 점진적 학습절차를 위해 평가 영상 데이터는 각 클래스에 하나씩 추가하고, 추가된 영상을 기존의 학습데이터들의 선형 합으로 표현하였다. 각 학습 절차마다 분류(Classification)를 수행 하였고, 각 절차별로 계산시간을 측정하였다. 실험은 쿼드코어 CPU(2.33GHz), 1.75RAM의 환경에서 MATLAB으로 수행되었다. Fig. 1은 학습 데이터 개수의 변화에 따른 QR 분해에 걸리는 계산 시간을 보여주고 있다. 특히 Batch QR 방식과의 비교를 통한 계산시간에서의 효율성을 실험적으로 제시하였다.
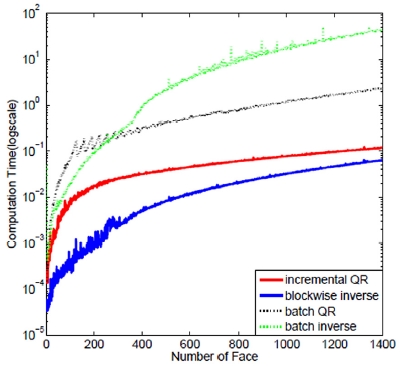
Comparison of computation time between batch QR, batch inverse, blockwise inverse and the proposed incremental QR decomposition
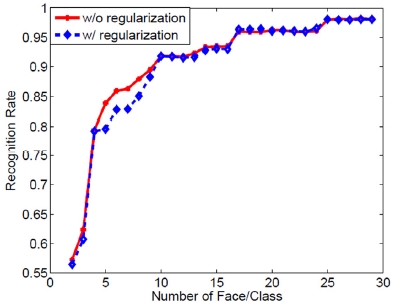
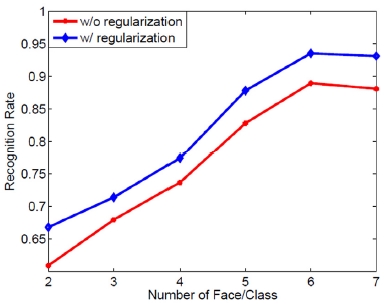
Fig. 1과 Fig. 2에서 보인 것처럼, 학습 데이터의 양이 많아질수록 계산량은 증가하고 있지만, 본 연구에서 제안한 점증적 QR 분해의 계산시간의 증가량은 배치(Batch) QR 분해 방법 대비 계산시간의 증가량이 매우 작음을 보여주고 있다. Fig. 1에서 나타난 것처럼 Blockwise inverse 방법보다는 여전히 계산 시간 소요가 큰 것으로 나타났고, Fig. 2에서는 Incremental QR 방식을 사용한 경우가 Batch QR 방식을 사용했을 경우보다 계산 시간이 감소되었음을 보여준다. 그러나, 학습 데이터가 늘어날수록 계산량의 증가폭은 Blockwise inverse 대비 점차 작아지고 있고, 전체 계산시간 또한 유사해 지고 있음을 확인할 수 있다. Fig. 3과 Fig. 4에서는 각 데이터베이스를 활용하여 얼굴인식률을 학습 데이터량의 변화에 따라 보여주고 있다. 각 실험에서는 정규화 식(Regularization term)을 포함한 결과와 포함하지 않은 결과도 비교하여 제시하고 있다.
Fig. 3과 Fig. 4에서 제시된 것처럼, 정규화 식을 포함한 경우와 포함하지 않은 경우 모두 학습 데이터의 수가 증가할수록 인식률은 증가하였다. 실험 결과 Fig. 3의 AR Face의 경우에는 학습데이터의 수가 증가할 때 Regularization term의 유무와 상관없이 비슷한 인식률을 보였으나, Fig. 4의 Extended Yale B 데이터의 경우에는 모든 학습 데이터 수의 변화에 대해서 Regularization term이 있을 경우에 더 좋은 인식률을 보였다. 이는 Extended Yale B의 경우 Class 별 학습데이터의 수가 AR Face 대비 작은 것이 그 원인일 것으로 추정된다.
특히 정규화 식이 포함되었을 경우 인식률은 조금 더 높거나 유사한 것으로 확인되었다. Table 1에서는 본 연구에서 제안한 L2-노름 방식을 활용하였을 때의 얼굴 인식률을 제시하고 있다. Table 1에서의 결과는 점진적인 학습을 통해 모든 학습 데이터를 활용했을 때의 결과이며, 이 결과는 Batch 학습 방식을 사용할 때와 결과가 동일하면서 학습에 소요되는 계산량 및 시간이 줄어들었음을 보여준다.
5. 결 론
본 논문에서는 점증적 L2-노름 방법을 활용하여 얼굴인식에 적용하여 그 결과를 제시하였다. 특히, 본 논문에서 제안한 L2-노름 방법은 점증적 QR 분해와 블록 행렬의 역행렬화(Blockwise matrix inversion)로 구성되어 있다. 제안한 방법으로 구현한 시뮬레이션은 얼굴 인식률과 계산시간이었으며, 학습데이터의 양이 많아지면서 발생할 수 있는 계산시간량에서 기존의 다른 방법들 대비 우세하거나 비교경쟁력이 있음을 확인하였다. 또한 얼굴인식률에서도 기존의 얼굴인식 방법들과 비교하였을 때 인식률의 결과에서 열세하지 않음을 확인하였다. 논문에서 제시한 이론적 모델과 실험에서 L2 노름 기반 방법은 계산효율에서의 장점을 보여주고 있고, 계산량의 감소로 인한 인식률의 저하가 없음을 보여주고 있다. 얼굴 인식 및 분류에 대한 연구는 최근 자율주행 자동차 또는 무인 자동차 시스템에서 필요성이 증대됨으로서, 학습량이 많아지는 상황에 대한 최적의 계산 해법에 대한 연구는 앞으로도 연구에 대한 필요성이 점차 증가할 것이다.15,16)
Acknowledgments
이 논문은 2018년도 정부(과학기술정보통신부)의 재원으로 정보통신기술진흥센터의 지원을 받아 수행된 연구임(2016-0-00564, 사용자의 의도와 맥락을 이해하는 지능형 인터랙션 기술 연구개발).
References
-
F. Schroff, D. Kalenichenko, and J. Philbin, “FaceNet: A Unified Embedding for Face Recognition and Clustering”, The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), p815-823, (2015).
[https://doi.org/10.1109/cvpr.2015.7298682]

- M. Turk, and A. Pentland, “Eigenfaces for Recognition”, Journal of Cognitive Neuroscience, 3(1), p71-86, (1991).
-
P. Belhumeur, J. Hespanda, and D. Kriegman, “Eigenfaces vs. Fisherfaces: Recognition Using Class Specific Linear Projection”, IEEE Transactions on Pattern Analysis and Machine Intelligence, 19(7), p711-720, (1997).
[https://doi.org/10.1109/34.598228]

- X. He, S. Yan, Y. Hu, P. Niyogi, and H. Zhang, “Face Recognition using Laplacianfaces”, IEEE Transactions on Pattern Analysis and Machine Intelligence, 27(3), p328-340, (2005).
- K. Q. Weinberger, and L. K. Saul, “Distance Metric Learning for Large Margin Nearest Neighbor Classification”, The Journal of Machine Learning Research, 10, p207-244, (209).
- S. -H. Park, and N. Kwak, “Local Appearance-based Face Recognition Using SVM and PCA”, Journal of Institute of Electronics Engineers of Korea - Signal Processing, 47(3), p54-60, (2010).
- M. Er, S. Wu, J. Lu, and H. Toh, “Face Recognition with Radial Basis Function(RBF)”, IEEE Transactions on Neural Networks, 13(3), p697-710, (2002).
-
J. Wright, A. Y. Yang, S. S. Sastry, and Y. Ma, “Robust Face Recognition Via Sparse Representation”, IEEE Transactions on Pattern Analysis and Machine Intelligence, 31(2), p210-227, (2008).
[https://doi.org/10.1109/tpami.2008.79]

- J. Cao, K. Zhang, M. Luo, C. Yin, and X. Lai, “Extreme Learning Machine and Adaptive Sparse Representation for Image Classification”, Neural Networks, 81, p91-102, (2016).
-
Q. Shi, A. Eriksson, A. Hengel, and C. Shen, “Is Face Recognition Really a Compressive Sensing Problem?”, IEEE Computer Society Conference on Computer Vision and Pattern Recognition, (2011).
[https://doi.org/10.1109/cvpr.2011.5995556]

-
L. Zhang, M. Yang, and X. Feng, “Sparse Representation or Collaborative Representation: Which Helps Face Recognition?”, International Conference on Computer Vision, (2011).
[https://doi.org/10.1109/iccv.2011.6126277]

- L. Lathauwer, B. Moor, and J. Vandewalle, “Computation of the Canonical Decomposition by Means of a Simultaneous Generalized Schur Decomposition”, SIAM Journal on Matrix Analysis and Applications, 26(2), p295-327, (2004).
-
A. Georghiades, P. Belhumeur, and D. Kriegman, “From Few to Many : Illumination Cone Models for Face Recognition Under Variable Lighting and Pose”, IEEE Transactions on Pattern Analysis and Machine Intelligence, 23(6), p643-660, (2001).
[https://doi.org/10.1109/34.927464]

- A. Martinez, and R. Benavente, The AR Face Database, CVC Technical Report #24, (1998).
- S. Oh, D. Lee, and D. Jo, “Achieving Driver Status via Face Detection Using Image Processing”, KSAE Spring Conference Proceedings, p617-618, (2018).
- S. Jung, G. Deepak, C. Park, and S. Park, “Adaptive ROI Technique for Lane Detection and Vehicle Detection”, KSAE Spring Conference Proceedings, p842, (2018).