Polyamide 6의 탄성계수에 대한 실험 온도와 수분 흡수의 영향

1. 서 론

수소연료전지자동차(FCEV, Fuel Cell Electric Vehicle)의 수소저장용기는 일반적으로 비금속 소재 라이너의 전체 면을 탄소섬유강화 복합재료로 감싼 용기 형태로 제작된다. 현재 라이너로 주로 사용되는 HDPE(High Density Polyethylene) 소재는 수소기체의 투과성이 높은 문제점을 갖고 있기 때문에 새로운 라이너 소재로 PA6(Polyamide 6)가 고려되고 있다. PA는 주사슬구조가 반복 아미드기와 섞인 열가소성 수지이다. 이는 나일론이라고도 불리며, 반복단위에 따라서 PA66, 6, 11, 12, 6/10, 6/12, 4/6 등으로 구분된다.¹⁾ PA6는 우수한 기계적 성질과 뛰어난 가격 경쟁력으로 여러 산업 분야에서 금속을 대체하여 그 사용이 증가하고 있다. 그러나 PA6는 그 화학 구조상(-CONH-) 공기 내 수분을 흡수하는 성질이 있다. PA6가 수분을 흡수하게 되면, 건조 상태에 비하여 물성이 변하게 된다. 따라서 PA6의 수분 흡수에 따른 물성 변화에 대한 많은 연구가 진행 중이다. Arhant 등²⁾은 PA6의 수분 흡수를 Fick’s Law, Arrhenius Law 및 Free Volume Theory와 비교하는 연구를 하였다. 해수의 온도변화에 따른 수분 흡수율을 Fick’s Law와 비교하였고, 이 때 발생한 차이를 Arrhenius Law와 Free Volume Theory로 보완하였다. Gac 등³⁾은 PA6의 수분 흡수에 따른 기계적 물성 변화를 연구하였다. 그 결과 수분 흡수율이 증가할수록 인장강도가 감소하는 것을 보였다. Lawrence 등⁴⁾은 PHEE(Poly Hydroxy Ester Ether)의 수분 흡수에 따른 기계적 물성 변화를 연구하였다. 이들은 수분 흡수가 증가할수록 유리천이온도와 인장강도가 감소하는 것을 보였다. Taktak 등⁵⁾은 PA6의 수분 흡수율에 따른 기계적 물성 변화를 연구하였다. 이들은 수분 흡수율이 높을수록 파괴 인성강도가 감소하는 것을 보였다. Miri 등⁶⁾은 80 μm 두께의 얇은 PA6 시편을 사용하여 수분 흡수에 따른 기계적 물성 변화를 연구하였다. 이들은 건조 상태의 시편에 비하여 수분을 흡수한 시편의 인장강도가 감소하는 것을 보였다. 김택기 등⁷⁾은 PA66에 EMMA(Ethylene Methyl Methacrylate)를 첨가하여 마찰마모 특성 및 수분 흡습의 변화를 연구하였다. 이들은 EMMA의 첨가를 통하여 PA66의 수분 흡습 개선 효과가 있음을 보였다.

PA6과 같은 고분자 재료로 제작한 복합재료에서 수분흡수에 따른 기계적 물성 변화에 대하여 많은 연구가 수행되었다. Arhant 등⁸⁾은 Carbon/PA6 섬유강화 복합재료에 흡수된 수분의 종류 및 수분 흡수율에 따른 기계적 물성 변화를 연구하였다. 이들은 해수의 흡수율 증가는 담수의 흡수율 증가보다 빠르게 진행되는 것을 확인하였고, 인장 및 압축 실험을 통해 건조 상태보다 수분 흡수 상태에서 기계적 물성이 50 % 이상 감소한 것을 확인할 수 있었다. Do 등⁹⁾은 CFRP(Carbon Fiber Reinforced Polyamide 6) 섬유강화 복합재료의 PP(Polypropylene)의 함유 및 수분 흡수에 따른 기계적 물성 변화를 연구하였다. 이들은 건조 상태에서는 PP의 함유율이 증가할수록 인장 강도가 감소하지만, 수분 포화 상태에서는 PP의 함유율이 증가할수록 인장강도가 증가하는 것을 보였다. Tanaka 등¹⁰⁾은 Carbon/PA 섬유강화 복합재료에서 PA의 종류 및 수분 흡수에 따른 기계적 물성 변화를 연구하였다. 이들은 수분 흡수가 증가할수록 인장 및 전단강도가 감소하는 것을 확인하였다. 그러나 수분 흡수 이전 상태의 인장강도와 수분 흡수 이후 건조 상태의 인장강도 크기는 PA의 종류에 따라 다른 결과를 나타내었다. Arif 등¹¹⁾은 Glass/PA6 섬유강화 복합재료의 수분 흡수에 따른 기계적 물성 변화를 연구하였다. 수분 흡수가 증가할수록 복합재료의 가소화로 인하여 PA6와 유리섬유 사이의 응집력이 감소하였고, 이로 인하여 굽힘 강도가 낮아지는 것을 보였다. Chaichanawong 등¹²⁾은 Glass/PA6 섬유강화 복합재료의 수분 흡수에 따른 기계적 물성 변화를 연구하였다. 이들은 유리섬유의 함유율이 높아질수록 연신율을 제외한 기계적 물성은 향상되었고, 수분 노출시간이 길어질수록 연신율을 제외한 기계적 물성은 감소하는 것을 확인하였다. 김성민과 김광제¹³⁾는 Glass/PA66 섬유강화 복합재료의 수분 흡수 이후, 건조 온도 및 건조 시간에 따른 기계적 물성 변화를 연구하였다. 이들은 수분 흡수 이후, 건조 온도 및 건조 시간이 증가할수록 인장강도 및 굴곡강도가 모두 증가하는 것을 보였다. 박상철 등¹⁴⁾은 Cloisite 93A/Nylon 66 나노복합체에서 Nylon 66 점도 및 Cloisite 93A 함량에 따른 기계적 물성 변화를 연구하였다. 이 연구에서는 Nylon 66 점도가 증가함에 따라서 인장강도는 증가하나 굴곡강도는 감소하는 것이 확인되었다. 김택기 등¹⁵⁾은 PA66에 Carbon Fiber 및 EMMA의 첨가에 따른 기계적 물성 변화를 연구하였다. 이들은 PA66에 EMMA를 첨가하여 인장강도는 유지하면서 연신율만 증가시킬 수 있음을 보였다.

본 연구에서는 세 제조 회사로부터 공급받은 PA6 시편의 수분 흡수율을 측정하였다. 또한 초기에 측정한 수분 흡수율 결과와 확산의 법칙을 이용하여, 포화 상태에 도달할 때까지 시간에 따른 PA6의 수분 흡수율을 예측하였다. 총 8개의 실험 온도(-60, -40, 0, 20, 40, 50, 85 및 95 °C)에서 건조 상태 및 상온의 담수에 3일과 16일 동안 담근 PA6 시편에 대해서 인장 실험을 수행하였다. 이를 통하여 실험 온도와 수분 흡수율이 PA6의 탄성계수에 미치는 영향을 살펴보았다. 또한 수분을 흡수한 PA6가 영하의 저온 환경에 놓일 때, 이를 얼음과 PA6로 구성된 복합재료로 가정하였다. 얼음과 PA6로 구성된 복합재료의 탄성계수를 예측하기 위해서 혼합법칙(Rule of Mixture)를 적용하였다. 실험으로 측정한 탄성계수와 혼합법칙으로 예측한 탄성계수 사이에서 발생하는 차이를 살펴보고 그 원인을 분석하였다.

2. 실 험

2.1 재료

세 제조 회사에서 공급받은 PA6의 시편을 사용하였다. ASTM(American Society for Testing and Materials) D638¹⁶⁾에서 명시한 Type I과 동일한 형상 및 크기를 갖도록 두께가 3.2 mm로 균일한 시편을 금형에 사출하여 제작하였으며(Fig. 1(a)), 이 시편을 사용하여 수분 흡수율을 측정하고 인장 실험을 수행하였다.

Fig. 1

Specimens and test system

3. 수분 흡수율 및 저온 탄성계수 예측

3.1 PA6의 수분 흡수율 변화 예측

상온의 담수에 담긴 PA6 시편에서 시간에 따른 수분 흡수율은 식 (1)을 통해 포화 상태에 도달할 때까지 주기적으로 시편의 질량을 측정하여 구할 수 있다. 식 (1)에서 w_absorbed는 수분 흡수율이고, M_t와 M₀는 각각 임의의 시간 t일 때 수분을 흡수한 PA6 시편의 질량과 건조 상태일 때 PA6 시편의 질량이다. 그러나 측정을 통하여 수분 흡수율을 구하기 위해서는, 포화 상태에 도달할 때까지 오랜 시간 동안 시편의 질량을 측정하여야 한다.

$\[ w_{absorbed}=\left(M_t-M_0\right)/M_0\times 100\left(\%\right) \]$

(1)

확산의 제2법칙을 사용하면, 시편의 질량 변화를 지속적으로 측정하지 않고 초기의 일정 시간 동안과 수분 흡수율이 포화 상태에서의 시편의 질량을 측정하여 임의의 시간에서의 수분 흡수율을 예측할 수 있다.

확산은 농도가 상대적으로 더 높은 곳에서 더 낮은 곳으로 입자가 이동하는 현상이다.¹⁸⁾ Adolf Eugen Fick은 확산 현상을 최초로 정량적으로 설명하였다. 이를 확산의 법칙(Fick’s Law of Diffusion)이라고 부른다. Fick은 확산의 법칙을 시간에 따라서 농도의 변화가 없는 정상 상태의 확산과 농도의 변화가 있는 비정상 상태의 확산으로 구분하여 설명하였다. 이들을 각각 확산의 제 1법칙과 제 2법칙이라고 한다.

비정상 상태의 확산을 설명하는 확산의 제 2법칙은 식 (2)와 같이 편미분 방정식으로 표현된다. 식 (2)에서 C는 물질의 농도이다.

$\[ \frac{\partial C}{\partial t}=D\frac{{\partial }^{2}C}{{\partial x}^2} \]$

(2)

위 식에 Laplace 변환을 적용하면 시간 변수를 제거할 수가 있게 되어, 비정상 상태의 확산의 법칙은 공간 변수만을 포함한 상미분 방정식으로 표현이 된다.¹⁹⁾ 이 상미분 방정식의 해는 쌍곡선 함수를 포함하게 된다. 이를 지수 함수를 이용하여 급수전개를 한 다음에 이를 초기에 균일한 농도를 갖는 얇은 시편 속으로의 비정상 상태의 확산 현상에 적용하면 식 (3)을 얻을 수 있다.

$\[ \frac{m_t}{m_{\infty }}=1-\frac{8}{{\pi }^2}\sum _{i=0}^{\infty }\frac{1}{{\left(2i+1\right)}^2}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{D{\left(2i+1\right)}^2{\pi }^{2}t}{h^2}\right) \]$

(3)

식 (3)에서 m_t와 m_∞는 각각 임의의 시간 t와 수분 흡수율이 포화 상태일 때 PA6에 흡수된 수분의 질량이다(건조 상태의 PA6의 질량을 제외한 흡수된 수분만의 질량). 식 (3)에서 t는 임의의 시간, h는 시편의 두께, 그리고 D는 확산계수(Diffusivity)이다.

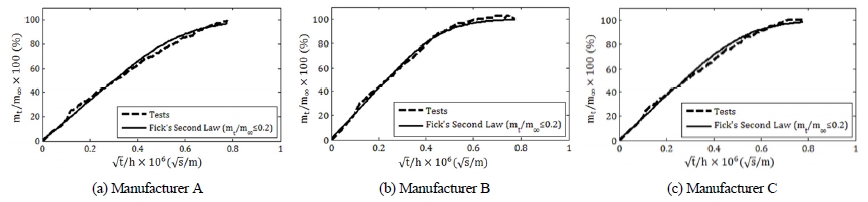
임의의 시간 t에서 PA6에 흡수된 수분의 질량 m_t와 수분 흡수율이 포화 상태일 때 PA6에 흡수된 수분의 질량 m_∞의 비(m_t/m_∞)는 시간의 제곱근과 시편 두께의 비($$ \sqrt{t}/h$$)와 서로 비선형 관계를 갖는다(Fig. 2). 그러나 m_t/m_∞ < 0.5인 초기 구간에서는, m_t/m_∞와 $$ \sqrt{t}/h$$는 서로 직선의 관계를 갖는 것으로 근사화할 수 있다. 이 초기 구간에서 직선의 관계식은 식 (4)로 표현될 수 있다.^2,8)

Fig. 2

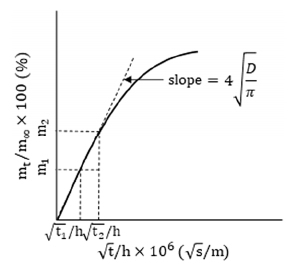
Ratio of mass of absorbed water at arbitrary time t to mass of absorbed water when substantially saturated as a function of the ratio of square root of time to specimen thickness

$\[ \frac{m_t}{m_{\infty }}=4\sqrt{\frac{D}{\pi }}\bullet \frac{\sqrt{t}}{h} \]$

(4)

담수에 담긴 PA6 시편에서, 초기 일정 시간 동안에 흡수된 수분의 질량과 수분 흡수율이 포화 상태일 때 흡수된 수분의 질량을 측정한 다음에 식 (4)를 이용한 선형회 귀분석으로 확산계수 D 값을 구할 수 있다. 이렇게 구한 확산계수의 값을 식 (3)에 대입하여, 임의의 시간에서의 수분 흡수율을 예측할 수 있다.

4. 결과 및 토론

4.1 수분 흡수율 측정

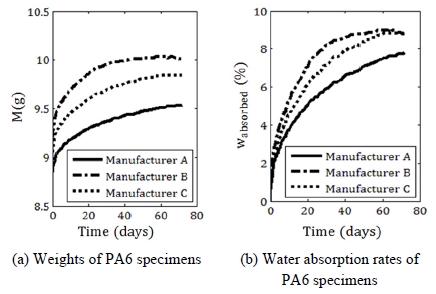
제조 회사 A, B 및 C로부터 공급받은 시편이 담수에 담긴 시간에 따른 시편의 질량(M_t)와 식 (1)의 수분 흡수율(w_absorbed)의 평균을 Fig. 3에 정리하였다.

Fig. 3

Weights of PA6 specimens and their water absorption rates as functions of immersion time

ASTM D570에서는, 2주 간격으로 시편의 질량 변화를 측정할 때 연속된 3회의 질량 증가가 1 % 미만이 되는 시점을 수분 흡수율의 포화 상태(Substantial saturation)로 정의한다.¹⁷⁾ 세 제조 회사 A, B 및 C의 시편이 수분 흡수율의 포화 상태에 도달하는 데에는 각각 69, 52 및 60일이 소요되었다. 또한 세 제조 회사 A, B 및 C의 시편이 포화 상태에서 흡수한 수분의 질량 (m_∞)은 각각 0.69, 0.81 및 0.80 g이었다. Table 1에 수분을 흡수한 PA6의 질량 (M), 수분 흡수율(w_absorbed), 포화 상태에 도달할 때까지의 시간 및 포화 상태에서 흡수된 수분의 질량(m_∞) 등을 정리하였다.

Table 1

Properties related to water absorption of PA6 specimens

4.2 PA6의 수분 흡수율 변화 예측

식 (4)를 이용하여, m_t/m_∞를 종속변수로 하고 $$ \sqrt{t}/h$$를 독립변수로 하여 질량의 비 m_t/m_∞가 0.2가 될 때가지 측정한 데이터를 사용하여 선형회귀분석으로 확산계수 D를 구하였다. 그 결과 제조 회사 A, B 및 C의 순으로 각각 D_A = 5.471 × 10^-13, D_B = 8.998 × 10^-13 및 D_C = 6.659 × 10^-13m²/s의 확산계수 값을 구할 수 있었다. 선형회귀분석에서 구한 확산계수의 값과 식 (3)을 이용하여, 포화 상태가 될 때까지 임의의 시간에서 흡수된 수분의 질량과 포화 상태에서 흡수된 수분의 질량의 비를 구하였다. 이 과정에서 식 (3)의 급수 전개에서는 11개의 항을 사용하였다(i = 0, 1, ..., 10). 식 (3)을 이용하여 구한 질량의 비와 담수 속에 담긴 PA6 시편의 질량을 지속적으로 측정하여 구한 질량의 비를 Fig. 4에 함께 도시하였다. 실험으로 측정한 수분 흡수율과 식 (3)을 이용하여 예측한 수분 흡수율의 평균 차이는 제조 회사 A, B, C의 순으로 각각 4.06, 2.84 및 3.63 %로 나타났다. 즉 시편을 담수에 담근 초기의 30시간(제조 회사 A 및 C) 또는 24시간(제조 회사 B) 동안의 시편 질량과 포화 상태에 도달했을 때의 시편 질량을 측정하여 임의의 시간에서 시편이 흡수한 수분의 질량을 잘 예측할 수 있음을 알 수 있다.

Fig. 4

Ratio of mass of absorbed water at arbitrary time t to mass of absorbed water when substantially saturated, measured and predicted using Fick’s second law of diffusion

4.3 탄성계수 측정

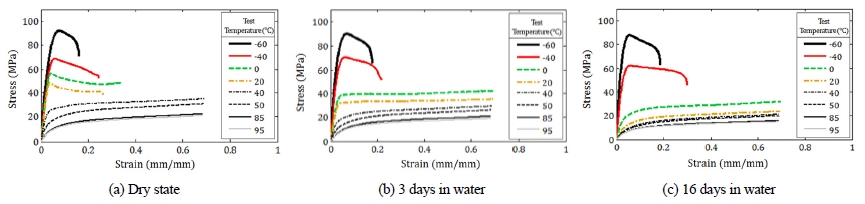
세 제조 회사로부터 공급받는 시편을 건조 상태 및 상온의 담수에 3일과 16일 동안 담근 상태에서, 총 8가지 실험 온도에서 인장실험을 수행하였다. 제조 회사 A의 시편에 대하여 인장실험의 결과로 획득한 응력-변형률 선도를 Fig. 5에서 도시하였다. 다른 두 제조 회사의 시편을 사용하여 획득한 응력-변형률 선도도 이와 유사한 형태를 나타내었다.

Fig. 5

Stress-strain curves of PA6 at different test temperatures, manufacturer A

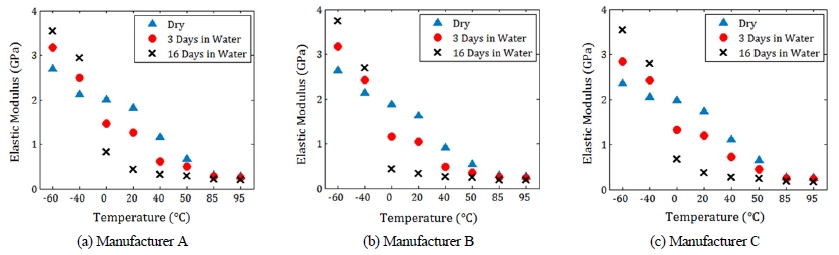
응력-변형률 선도의 초기 구간의 기울기인 탄성계수 값을 구하여, Fig. 6과 Table 2에서 정리하였다. 모든 제조회사 및 모든 수분 흡수율(또는 물에 담근 시간)의 시편에서 실험 온도가 증가할수록 탄성계수 값이 감소하였다.

Fig. 6

Measured elastic modulus of PA6 with different immersion time at different test temperatures

Table 2

Measured elastic modulus of PA6 (GPa)

모든 제조 회사의 시편에서 실험 온도가 빙점(0 °C) 이상의 온도(0, 20, 40, 50, 85 및 95 °C)일 때, 수분 흡수율(또는 물에 담근 시간)이 증가할수록 탄성계수가 감소하였다. 그러나 실험 온도가 빙점보다 낮은 저온(-60 및 -40°C)일 때에는, 수분 흡수율(또는 물에 담근 시간)이 증가할수록 탄성계수가 오히려 증가하였다. 예를 들면 제조회사 A의 시편이 담수에 16일 동안 담겨서 수분 흡수율이 4.63 %인 시편의 경우 -40과 -60 °C에서의 탄성계수는 각각 2.95과 3.54 GPa이다. 동일한 온도에서 건조 상태 시편의 경우, -40과 -60 °C에서의 탄성계수는 각각 2.14와 2.71 GPa이다. 수분 흡수율(또는 물에 담근 시간)이 증가할수록 탄성계수가 증가하는 이유는, 빙점 이하의 온도(-40과 -60 °C)에서는 PA6에 흡수된 수분이 모두 얼음으로 변경되며 얼음의 탄성계수가 6.50 ~ 10.39 GPa로²¹⁾ 건조 상태의 PA6의 탄성계수인 2.14와 2.71 GPa 보다 더 큰 값을 갖기 때문이다. 모든 제조 회사의 시편에서 동일한 경향이 관측되었다.

4.4 수분을 흡수한 PA6의 저온 탄성계수 예측

영하의 온도(-60 및 -40 °C)에서 식 (5)와 (6)의 혼합법칙을 사용하여 수분을 흡수한 PA6의 탄성계수를 예측해 보았다. 식 (5)와 (6)을 사용할 때, Table 2로부터 해당 온도에서 건조 상태(담수에 담근 시간이 0) PA6의 탄성계수를 이용하였다. 얼음은 그 결정 구조 등에 따라서 재료 물성의 산포가 매우 크다. 따라서 어떤 특정 온도에서 얼음의 탄성계수를 정확하게 구하는 것이 어려우므로, 본 연구에서는 온도와 관계없이 얼음의 탄성계수가 일정하다고 가정하였으며, 탄성계수 값으로 8.45 GPa을 사용하였다.²¹⁾

영하의 온도(-60 및 -40 °C)에서 수분 흡수율(또는 물에 담근 시간)의 변화에 따라서 측정한 탄성계수와 혼합법칙을 사용하여 예측한 탄성계수를 Fig. 7에서 정리하였다.

Fig. 7

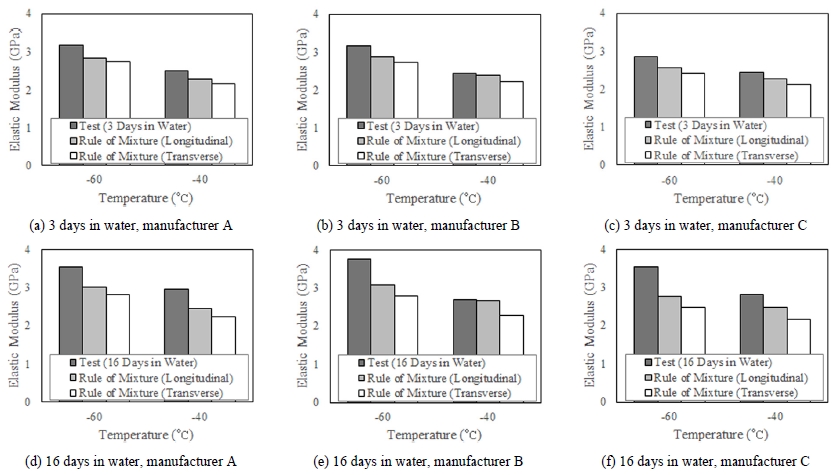
Measured and predicted elastic moduli. Predicted elastic modulus was found using rule of mixture (ROM)

온도가 감소함에 따라서, 실험에서 측정한 탄성계수와 혼합 법칙을 사용하여 예측한 탄성계수는 모두 증가하는 경향을 보였다. 얼음의 탄성계수가 온도와 관계없이 일정한 값을 갖는 것으로 가정하였기 때문에, 온도가 감소함에 따라서 혼합 법칙을 사용하여 예측한 탄성계수가 증가하는 이유는 온도가 감소함에 따라서 건조 상태의 PA6의 탄성계수가 증가하기 때문이다.

얼음이 PA6 내부에서 입자의 형태로 존재하므로, 실험으로 측정한 탄성계수는 혼합 법칙으로 예측한 섬유방향의 탄성계수(식 (5)의 E_x)와 섬유에 수직한 방향의 탄성계수(식 (6)의 E_y) 사이의 값을 가질 것으로 예측이 되었다.

그러나 실험으로 측정한 탄성계수는 저온(-40 및 -60°C)에서 혼합법칙으로 예측한 E_x와 E_y보다 더 큰 값을 갖는 것으로 나타났다.

Fig. 7(a)에 의하면, 담수에 3일 동안 담겨 있던 제조 회사 A의 시편의 경우에 -60 °C에서 혼합 법칙으로 예측한 섬유와 평행한 방향의 탄성계수가 2.85 GPa이었으나 실제 실험으로 측정한 탄성계수는 3.18 GPa로 약 11.58 % 더 큰 값을 갖는 것으로 나타났다. 이 차이를 Fig. 8에 나타내었다. 담수에 담긴 기간이 길수록 이 차이는 더 커지는 경향을 갖는다. Fig. 7(d)에 의하면 담수에 16일 동안 담겨 있던 제조 회사 A의 시편의 경우에 -60 °C에서 혼합법칙으로 예측한 섬유와 평행한 방향의 탄성계수가 3.00 GPa이었으나 실제 실험으로 측정한 탄성계수는 3.54 GPa로 약 18.00 % 더 큰 값을 갖는 것으로 나타났다(Fig. 8). 이러한 경향은 세 제조 회사의 시편에서 모두 동일하게 나타났다.

Fig. 8

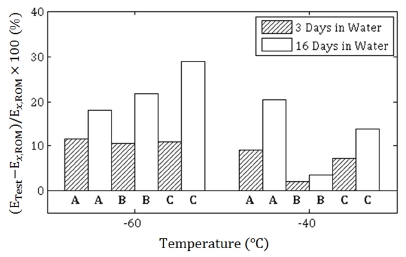
Difference between measured and predicted elastic moduli with specimens of manufacturers A, B and C. The predicted elastic modulus was calculated using Eq. (5)

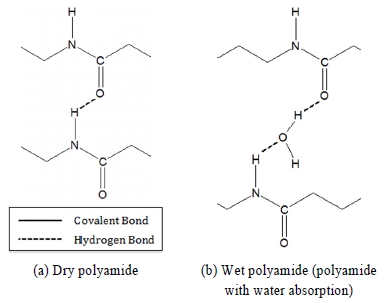
혼합 법칙으로 탄성계수를 예측할 때에는, 구성 요소들의 탄성계수와 체적분율(Volume Fractions)만을 고려한다. 그러나 PA6가 수분을 흡수했을 때에는, 흡수된 물 분자와 PA6가 각각 별도로 존재하기 않고 물 분자가 PA6의 사슬구조에 결합된 형태로 존재한다. PA와 수분 분자의 결합된 모습을 Fig. 9에 나타내었다. 이 상태에서 온도가 -40 또는 -60 °C 정도로 크게 낮아지게 되면 수분이 얼음으로 변경되고, 얼음과 PA6의 사슬구조 사이의 결합력이 매우 강해지게 된다. 이 때문에 수분을 흡수한 PA6 시편을 사용하여 저온에서 실험으로 측정한 탄성계수가 동일 온도에서 혼합 법칙으로 예측된 탄성계수보다 더 큰 값을 갖는다. 이러한 경향은 수분의 흡수량이 많아질수록 더 커지게 된다(Fig. 8). Fig. 8에 의하면, -40와 -60 °C 온도의 모든 제조 회사의 시편에서 16일 동안 담수에 담긴 시편이 3일 동안 담수에 담긴 시편보다 혼합법칙으로 예측한 섬유와 평행한 방향의 탄성계수(식 (5)의 E_x)와 실험으로 측정한 탄성계수의 차이가 더 큰 것을 확인할 수 있다.

Fig. 9

Interaction of polyamide structure with water molecules14)

5. 결 론

세 제조 회사로부터 공급받은 PA6 시편의 수분 흡수율을 확산의 제2법칙을 사용하여 예측하였으며, 건조 상태 및 상온의 담수에 3일과 16일 동안 담근 시편을 사용하여 인장실험을 수행하여 탄성계수를 획득하여 다음과 같은 결론을 얻을 수 있었다.

PA6 시편에서 초기의 수분 흡수율을 측정하여 선형회귀분석으로 확산계수를 구하였다. 이 확산계수를 사용하여 장기간 동안의 수분 흡수율을 정확하게 예측할 수 있음을 확인할 수 있었다.

실험 온도가 증가할수록 PA6시편의 탄성계수가 감소함을 확인하였다.

빙점(0 °C) 이상의 실험온도에서는 수분 흡수율이 증가할수록 탄성계수가 감소하였다. 이는 흡수된 수분이 가소제(Plasticizer)역할을 하기 때문이다. 빙점 이하의 온도에서는, 수분 흡수율이 증가할수록 탄성계수가 증가하였다. 이는 흡수된 수분이 얼음 결정으로 변화하며, 얼음의 높은 탄성계수가 수분을 흡수한 PA6의 탄성계수를 증가시키기 때문이다.

빙점 이하의 온도에서 혼합법칙으로 수분을 흡수한 PA6의 탄성계수를 예측하였다. 실험으로 측정한 탄성계수가 혼합 법칙을 사용하여 예측한 탄성계수보다 더 큰 값을 가졌다. 또한 이 차이는 수분 흡수율이 증가할수록 더 커졌다. 그 이유는 PA6에 흡수된 물 분자들이 PA6의 사슬구조에 결합된 형태로 존재하는데, 빙점 이하의 온도에서는 수분이 얼음으로 변화되면서 얼음과 PA6의 사슬구조 사이에 결합력이 강해지기 때문이다.

Acknowledgments

이 논문은 2018년도 한국기술교육대학교 교수연구제 파견연구비 지원 및 산업통상자원부와 한국산업기술진흥원의 수소연료전지차 부품실용화 및 산업기반육성사업(과제번호 R0006462)으로 수행된 연구 결과입니다.

References

• C. C. Ibeh, Thermoplastic Materials, Chap.16, CRC Press, Boca Raton, (2013).
• M. Arhant, P. -Y. Le Gac, M. Le Gall, C. Burtin, C. Briançon, and P. Davies, “Modelling the Non Fickian Water Absorption in Polyamide 6”, Polymer Degradation and Stability, 133, p404-412, (2016). [https://doi.org/10.1016/j.polymdegradstab.2016.09.001]
• P. -Y. Le Gac, M. Arhant, M. Le Gall, and P. Davies, “Yield Stress Changes Induced by Water in Polyamide 6: Characterization and Modeling”, Polymer Degradation and Stability, 137, p272-280, (2017). [https://doi.org/10.1016/j.polymdegradstab.2017.02.003]
• S. St. Lawrence, J. L. Willett, and C. J. Carriere, “Effect of Moisture on the Tensile Properties of Poly(hydroxy ester ether)”, Polymer, 42(13), p5643-5650, (2001). [https://doi.org/10.1016/s0032-3861(00)00836-3]
• R. Taktak, N. Guermazi, J. Derbeli, and N. Haddar, “Effect of Hygrothermal Aging on the Mechanical Properties and Ductile Fracture of Polyamide 6: Experimental and Numerical Approaches”, Engineering Fracture Mechanics, 148, p122-133, (2015). [https://doi.org/10.1016/j.engfracmech.2015.09.001]
• V. Miri, O. Persyn, J. -M. Lefebvre, and R. Seguela, “Effect of Water Absorption on the Plastic Deformation Behavior of Nylon 6”, European Polymer Journal, 45(3), p757-762, (2009). [https://doi.org/10.1016/j.eurpolymj.2008.12.008]
• T. Kim, and H. Ahn, “Wear and Water Absorption Characteristic of PA66/Polyolefin-polyblends Using Worm Gear of C-EPS System”, KSAE Annual Conference Proceedings, p949-955, (2011).
• M. Arhant, P. -Y. Le Gac, M. Le Gall, C. Burtin, C. Briançon, and P. Davies, “Effect of Sea Water and Humidity on the Tensile and Compressive Properties of Carbon-polyamide 6 Laminates”, Composites Part A: Applied Science and Manufacturing, 91, p250-261, (2016). [https://doi.org/10.1016/j.compositesa.2016.10.012]
• V. -T. Do, H. -D. Nguyen-Tran, and D. -M. Chun, “Effect of Polypropylene on the Mechanical Properties and Water Absorption of Carbon-fiber-reinforced-polyamide-6/ Polypropylene Composite”, Composite Structures, 150, p240-245, (2016). [https://doi.org/10.1016/j.compstruct.2016.05.011]
• K. Tanaka, S. Mizuno, H. Honda, T. Katayama, and S. Enoki, “Effect of Water Absorption on the Mechanical Properties of Carbon Fiber/Polyamide Composites”, Journal of Solid Mechanics and Materials Engineering, 7(5), p303-304, (2013). [https://doi.org/10.1299/jmmp.7.520]
• M. F. Arif, F. Meraghni, Y. Chemisky, N. Despringre, and G. Robert, “In Situ Damage Mechanisms Investigation of PA66/GF30 Composite: Effect of Relative Humidity”, Composites Part B: Engineering, 58, p487-495, (2014). [https://doi.org/10.1016/j.compositesb.2013.11.001]
• J. Chaichanawong, C. Thongchuea, and S. Areerat, “Effect of Moisture on the Mechanical Properties of Glass Fiber Reinforced Polyamide Composites”, Advanced Powder Technology, 27(3), p898-902, (2016). [https://doi.org/10.1016/j.apt.2016.02.006]
• S. M. Kim, and K. J. Kim, “Effects of Moisture and Temperature on Recrystallization and Mechanical Property Improvement of PA66/GF Composite”, Polymer Korea, 39(6), p880-888, (2015). [https://doi.org/10.7317/pk.2015.39.6.880]
• S. C. Park, H. G. Kim, and K. E. Min, “Nylon 66 Viscosity Effect on Mechanical Properties of Nylon 66/Cloisite 93A Nanocomposite”, Polymer Korea, 37(1), p100-112, (2013). [https://doi.org/10.7317/pk.2013.37.1.100]
• T. Kim, D. Ha, and S. Kim, “Rigidity and Oil Resistance Characteristic of Carbon Fiber Reinforced Using Lip Seal of ABS System”, KSAE Annual Conference Proceedings, p2125-2128, (2012).
• ASTM Standards: D638 Test Method for Tensile Properties of Plastics. ASTM Book of Standards, 08.01, (2002).
• ASTM Standards: D570 Test Method for Water Absorption of Plastics. ASTM Book of Standards, 08.01, (1998).
• J. Schaffer, A. Saxena, T. Sanders, S. Antolovich, and S. Warner, The Science and Design of Engineering Materials, Chap.4, McGraw-Hill Education, New York, (2000).
• J. Crank, The Mathematics of Diffusion, Chap.2 and 4, Oxford University Press, London, (1975).
• N. E. Dowling, Mechanical Behavior of Materials, Pearson, Edinburgh Gate, p219-221, (2013).
• L. W. Gold, “On the Elasticity of Ice Plates”, Canadian Journal of Civil Engineering, 15(6), p1080-1084, (1988). [https://doi.org/10.1139/l88-140]