[ Article ]

Transactions of The Korean Society of Automotive Engineers - Vol. 27, No. 4, pp.267-272

ISSN: 1225-6382 (Print) 2234-0149 (Online)

Print publication date 01 Apr 2019

Received 05 Nov 2018 Revised 07 Dec 2018 Accepted 10 Dec 2018

DOI: https://doi.org/10.7467/KSAE.2019.27.4.267

고강도강에 적용된 경량 차체부품의 정적 및 동적 강성에 관한 연구

이현철^*^{, 1)}

; 김민근¹⁾

; 고건영¹⁾

; 한승남²⁾

1)자동차부품연구원 소재융합연구센터
2)현성테크노 기술팀

A Study on the Static and Dynamic Stiffness of Lightweight Vehicle Body Part Applied to High Strength Steel

Hyun-chul Lee^*^{, 1)}

; Min-geun Kim¹⁾

; Gun-young Go¹⁾

; Seung-nam Han²⁾

1)Material Convergence Center, Gwangju-Jeonnam Division, Korea Automotive Technology Institute, 55 Jingoksandanjungang-ro, Gwangsan-gu, Gwangju 62465, Korea
2)Research Center, Hyunsung Techno Co, Ltd, 30 Cheomdanyeonsin-ro, 398beon-gil, Buk-gu, Gwangju 61088, Korea

Correspondence to: ^*E-mail: hclee@katech.re.kr

Copyright Ⓒ 2019 KSAE / 161-04
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.

Abstract

In order to cope with the recent fuel efficiency and exhaust emission regulation of vehicles, vehicle weight reduction has become an indispensable item rather than an option. Domestic and overseas automakers are continuously conducting research to address these lightweight issues. Among these methods for weight reduction, the application of high-strength steel with a relatively low price and lightweight effect is increased. Strength is improved when the material is replaced with high-strength steel; however, it is difficult to expect stiffness improvement to enhance the driving safety required for the automobile. In this paper, the study on stiffness improvement through the finite element analysis and the test evaluation of stiffness according to the application of high-strength steel body part are carried out. It is also confirmed that the stiffness improvement according to the application of high-strength steel is only possible through structural optimization.

Keywords:

Lightweight, High strength steel, Vehicle body parts, Static stiffness, Dynamic stiffness

키워드:

경량화, 고강도강, 차체부품, 정강성, 동강성

1. 서 론

최근 자동차 연비규제 강화와 안전편의 장비 적용 확대에 따라 차량 중량 증가에 대응하기 위한 방안으로 자동차 경량화가 주목 받고 있다. 자동차 경량화는 소재의 치환, 구조 최적화 및 공법 적용을 통하여 다양하게 적용되고 있다. 국내외 글로벌 완성차업체에서는 이러한 차체 경량화를 위해 가격상승을 최소화하면서 경량화 효과가 높은 고강도강을 차체에 두루 적용하고 있다.^1,2) 고강도강은 기존의 일반강을 대비 강도를 강하게 만든 소재로 부품 두께를 줄일 수 있어 차량의 경량화와 더불어 강도(Strength)향상에 크게 기여하고 있는 소재이다. 이러한 소재의 강도는 차량 충돌 등의 특성 즉, 탄성변형 영역을 넘어 영구변형이 발생하는 소성변형 영역에서 강도의 특성이 향상된다. 하지만 자동차에서 강성(Stiffness)향상은 조금 다른 얘기이다. 자동차에서 요구하는 강성(Stiffness)은 주행성능 및 주행안정성, 진동, 소음 등에 기여하는 특성으로 소성변형이 일어나기 이전인 탄성변형 영역에서 하중에 의한 변형의 저항정도를 의미한다.

따라서 본 논문에서 경량화 및 강도향상에 기여하는 고강도강 차체부품이 형상에 대한 변경없이 소재 치환에 따른 강성에는 어떠한 영향을 미치는지에 대한 평가를 수행하였다. 이를 위해 차체부품의 정동강성해석 및 실험평가를 통해 강성에 대한 평가를 수행하였으며 이에 따른 강성 향상 방안에 대한 연구를 수행하였다.

2. 본 론

2.1 정/동강성 실험 및 해석모델

정/동강성 해석 및 실험을 위해 강도향상용 차체부품인 크로스크로스멤버를 선정하였다. 경량화를 위해 인장강도 440 MPa, 두께 1.6 mm 소재를 형상변경없이 인장강도 780 MPa, 두께 1.2 mm의 고강도강 소재로 변경 적용한 부품의 정동강성 해석 및 실험을 수행하였으며 인장강도 440 MPa, 두께 1.6 mm의 크로스멤버는 정/동강성 해석방법을 통해 고강도강 적용품과 강성에 대한 비교평가를 수행하였다.

2.2 실험 및 해석조건

2.2.1 정강성실험 및 해석조건

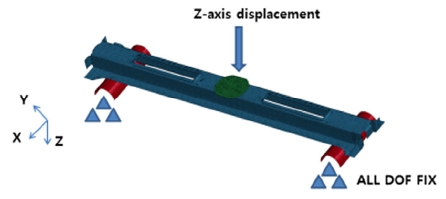
정강성실험을 위하여 실험 대상품인 크로스멤버의 중앙부에서 양쪽으로 350 mm 지점의 지름 25 mm의 지지대에 놓고 크로스멤버 중앙부에 지름 90 mm 원형 판재형상의 하중지그로 약 100 ~ 700 N까지 약 100 N간격으로 크로스멤버에 수직한 방향으로 하중을 부여하여 하중에 따른 변형량을 다이얼게이지를 통해 측정하였다.

정강성해석은 기본적으로 정강성실험 상의 경계조건과 동일하게 모사하였다. 지지대의 경계조건은 모든 방향을 고정조건으로 부여하였으며 하중지그는 방향에 수직방향으로 하중이 부여되게 변위제어 방식을 적용하였다. 또한 해석방법은 동적인 거동을 모사할 수 있는 Dynamic Implicit Analysis 방법을 사용하였다. 해석모델은 2D Shell Mid-surface 형태로 모델링하였으며 격자는 Quad 형상 및 3 mm사이즈로 설정하였다.

해석에 사용된 SW는 LS-DYNA를 사용하였으며 적용된 물성카드는 MAT-24 PIECEWISE_ LINEAR_PLASTIC을 적용하였으며 해당 물성치는 아래 표와 같다.

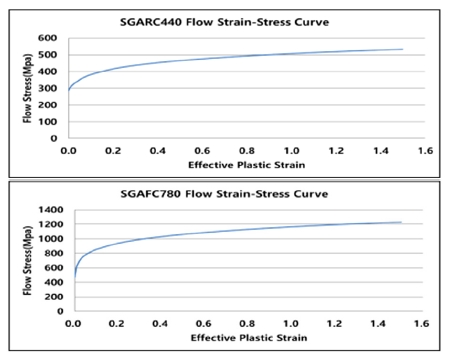
해석 적용 물성값 도출을 위하여 인장실험을 통해 Stain-Stress Curve 선도를 도출하였으며 해당 선도는 아래 Fig. 4와 같다.

Fig. 1

Static & Dynamic stiffness test parts

Fig. 2

Static stiffness test configuration

Fig. 3

Static stiffness FEM analysis condition

Fig. 4

Flow strain-stress curve

2.2.2 동강성시험 및 해석조건

동강성의 경우, Modal Test 통해 도출한 1차 고유진동수로 판단하는 경우가 많으며, 해당 고유진동수는 구조 강성과 연관되어 있으며 이러한 고유진동수 파악을 위하여 Modal Test를 진행하였다.^3,4) 크로스멤버 부품 자체의 고유진동수를 파악하기 위한 실험의 경계조건은 와이어 형태로 봉에 매달아 자유단 형태 모사하였다. 해당 경계조건에서 IMPact Hammer가진을 통해 입력신호를 부여하고 입력신호에 대한 고유진동수의 출력신호는 총 8개의 가속도센서를 통해 획득하였으며 가속도 센서 부착위치의 Geometry정보를 분석소프트웨어에 입력하여 Mode 형상을 분석하였다. 이러한 입출력신호를 LMS Test. lap_IMPact Testing 장비의 Frequency Response Function 신호분석 프로그램을 통해 1st mode의 고유진동수 범위 및 1st mode 형상을 분석하였다.

동강성 해석은 Modal Anlysis를 통해 강체변형 특성을 제외한 1st mode의 고유진동수에 대한 해석을 수행하였다.

해석에 사용된 소트트웨어는 정강성해석에 사용한 LS-Dyna를 사용하였고 적용된 물성카드는 MAT-3 PLASTIC_KINEMATIC을 적용하였으며 해당 물성치는 위의 Table 1과 같다.

Table 1

Material properties

모델 및 격자조건 또한 정강성 해석과 동일하게 설정하였으며, 경계조건만 자유단 형태로 설정하여 Modal 해석을 수행하였다.

2.3 실험 및 해석결과

2.3.1 정강성실험 결과

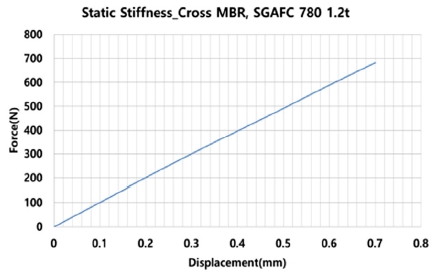
경량화 고강도강 적용품인 인장강도 780 MPa, 두께 1.2 mm인 크로스멤버를 약 100 ~ 700 N범위에서 약 100 N 간격으로 하중을 부여하여 굽힘정강성실험을 수행한 결과값은 Fig. 6과 같다.

Fig. 5

Dynamic stiffness test configuration

Fig. 6

Static stiffness test result

2.3.2 정강성해석 결과

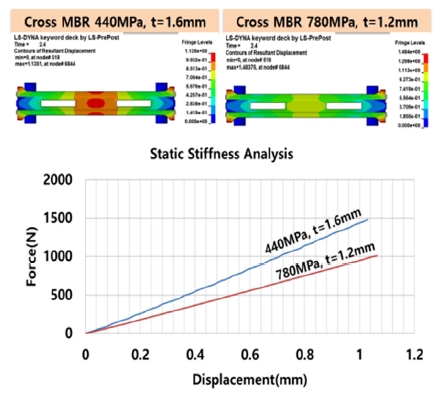
인장강도 440 MPa, 두께 1.6 mm와 경량화 고강도강 적용품인 인장강도 780 MPa, 두께 1.2 mm의 크로스멤버의 정강성 해석결과는 Fig. 7과 같다.

Fig. 7

Static stiffness FEA results

강성값은 하중을 변위량으로 나눈 값, 즉 위 Fig. 7의 그래프선도에서 기울기값이 강성을 나타내는 수치이므로 경량화하기 전인 인장강도 440 MPa, 두께 1.6 mm의 크로스멤버가 경량 고강도강 적용품인 인장강도 780 MPa, 두께 1.2 mm의 크로스멤버보다 강성값이 크다는 것을 알 수 있다.

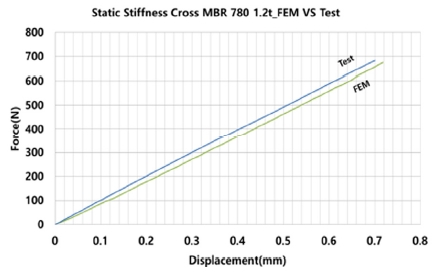
정강성해석에 대한 정확도를 검증하기 위하여 경량 고강도강 실험값과 해석값을 비교한 결과를 Fig. 8에 나타내었다. Fig. 8에서 보는 바와 같이 실험값과 해석값이 거의 일치함을 확인하였으며 이러한 실험과 해석간 상관관계 분석을 통해 해석에 대한 신뢰도를 확보할 수 있었다.

Fig. 8

Static stiffness test VS FEA results

2.3.3 동강성실험 결과

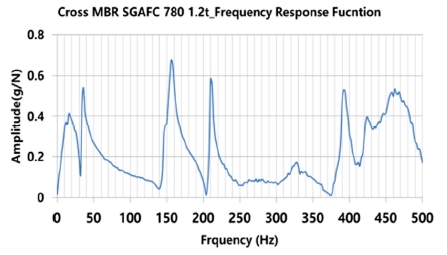
경량 고강도강 적용품인 인장강도 780 MPa, t=1.2 mm인 크로스멤버의 Modal Test를 통해 1st mode 고유진동수를 분석한 주파수 응답 특성 결과를 Fig. 9에 나타내었으며 강체 거동을 제외한 경량 고강도강 적용품의 1st mode 고유진동수는 34.3 Hz 나타내었다.

Fig. 9

Dynamic stiffness test result

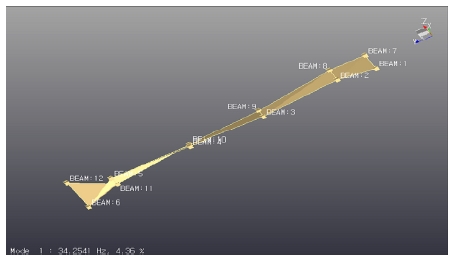
또한 동강성시험 시 Mode형상 분석을 위해 실험 대상품에 장착한 가속도센서의 Geometry정보를 분석소프트웨어 입력하여 1st mode의 모드 형상을 분석한 결과를 Fig. 10에 나타내었다. Fig. 10에서 보는 바와 같이 1st mode의 모드 형상은 비틀림 변형이 발생하였다. 일반적으로 1st mode변형인 굽힘 변형모드가 아닌 비틀림 변형이 발생한 이유는 크로스멤버의 형상에서 보여지는 바와 같이 비틀림 변형에 더욱 취악한 구조이므로 1st mode의 변형이 비틀림이 발생한 것으로 판단된다.

Fig. 10

Cross MBR 780 1st mode shape

2.3.4 동강성해석 결과

실험과 마찬가지로 인장강도 440 MPa, 두께 1.6 mm와 경량 고강도강 적용품인 인장강도 780 MPa, 두께 1.2 mm인 크로스멤버의 Modal 해석한 결과값은 각각 44.3 Hz와 34.0 Hz로 나타났으며 이에 대한 해석 결과는 Fig. 11에 나타내었다.

Fig. 11

Dynamic stiffness analysis results

위 해석결과로부터 인장강도 440 MPa, 두께1.6 mm인 크로스멤버가 경량화 고강도강 적용품인 인장강도 780 MPa, 두께 1.2 mm인 크로스멤버보다 1st mode 고유진동수 주파수 범위가 높다. 이 주파수의 범위는 강성값에 비례하므로 경량화된 고강도강 적용품의 크로스멤버가 경량화 전 적용품보다 강성값이 낮다는 것을 알 수 있다.

동강성해석에 대한 정확도를 검증하기 위하여 경량 고강도강 실험값과 해석값을 비교한 결과, 각각 34.3 Hz와 34.0 Hz의 값을 나타내었으며, 오차가 거의 발생하지 않음을 알 수 있으며 이러한 실험과 해석간 상관관계 분석을 통해 해석에 대한 신뢰도를 확보할 수 있었다.

3. 고 찰

3.1 강성실험 및 해석결과 고찰

3.1.1 정동강성실험 및 해석결과 고찰

앞서 언급한 바와 같이 강성은 탄성변형 영역에서 외력에 의한 변형에 대한 저항정도를 의미하며 변형의 종류에 관계없이 비강성값은 탄성계수와 밀도와의 함수로 정의되어 진다.^5-7) 정/동강성값이 탄성계수와 밀도와의 함수로 정의된다는 것을 아래와 같은 수식으로 표현하였다.

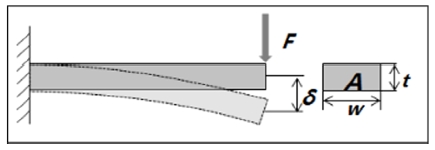
강성은 변형을 최소화하는 정도이기 때문에 차량에서 발생할 수 있는 변형의 종류인 인장, 압축, 굽힘, 비틀림에 따라 외력-변위 관계가 존재함에 따라서 변형에 대한 비강성(Specific stiffness)을 먼저 정의할 필요가 있다. 예를 들어 판재 혹은 빔형태의 차체부품이 굽힘을 받는다는 전제하에 비강성에 수식을 분석해 보면 아래 수식 (1), (2)와 같이 정의된다.

Fig. 12

Static bending stiffness of a panel shape

m = A L ρ = W t L ρ, I = W t 3 12 K = F δ = c E I L 3 ≥ K * c E I L 3 = c E L 3 W t 3 12 = c 12 E L 3 W t l ρ 3 W 2 L 3 ρ 3 = c 12 E L 3 m 3 W 2 L 3 ρ 3 ≥ K *

(1)

m 3 ≥ K * 12 c W W 3 L 6 ρ 3 E m ≥ K * 12 c W 1 / 3 W L 2 ρ E 1 / 3 K * m ∝ E 1 / 3 ρ

(2)

위 수식과 같이 판재가 굽힘을 받는 경우, 비강성은 탄성계수 1/3승에 비례하고 밀도에 반비례하는 관계를 보인다. Table 2는 판재 및 빔형태의 차체 구조물의 차량에서 발생 가능한 변형의 종류에 따른 비강성과 비강도와 의 관계를 나타내었다.

Table 2

Specific stiffness correlation according to shape type

위 표에서와 같이 차체에서 발생할 수 있는 변형의 조건에 관계없이 비강성은 탄성계수(또는 전단계수) 및 밀도와의 함수로 정의될 수 있다.

3.1.2 동강성실험 및 해석결과 고찰

마찬가지로 차체부품이 진동 등의 동적인 변형이 발생한 경우에도 비강성은 탄성계수(또는 전단계수) 및 밀도와의 함수로 정의될 수 있다.⁸⁾

Fig. 13

In case of vibration for the panel

구조물이 빔이나 판넬 등의 형상에서 진동모드는 굽힘이나 비틀림 모드가 먼저 발생하고 인장/압축 모드는 그 후에 발생하므로 동강성의 하중조건이 굽힘이라고 가정했을 때의 수식을 분석해 보면 수식 (3), (4)와 같은 관계를 알 수 있으며, 이는 동강성 또한 탄성계수와 밀도와의 함수로 정의됨을 알 수 있다.

ω = K m K = F δ = c E I L 3, m = ρ L 2 t, I = L t 3 12 ω = c E I L 3 1 ρ L 2 t = c 12 E ρ t 2 L 4 = c 12 E ρ 1 L 4 t 2 = c 12 E ρ 1 L 4 m 2 ρ 2 L 4 ≥ ω * m ≥ ω * 12 c ρ 3 E L 3 = ω 3 12 c L 4 ρ 3 / 2 E 1 / 2

(3)

ω * ∝ E 1 / 2 ρ 3 / 2

(4)

대부분의 강재에서 강성에 영향을 미치는 이러한 탄성계수와 밀도의 물성은 변화없이 일정한 값을 갖는다. 강재의 열처리나 가공방법 등에 따라서 변하지 않는 성질이다. 자동차 차체의 경량화를 위해 일반 강재에서 고강도강으로 소재를 치환할 경우에도 마찬가지로 탄성계수와 밀도의 물성변화는 특수한 경우를 제외하고는 거의 변화 없다. 즉 동일한 형상조건에서 일반강재에서 고강도강으로 치환 시 비강성의 변화는 없으며 경량화를 위한 소재의 두께를 얇게 적용하므로써 비강성은 오히려 감소하게 된다는 것을 수식 (5)와 같이 나타낼 수 있다.

K m i l d s t e e l K h i g h S t r e n g t h s t e e l = E m 1 / q ρ m m m E h 1 / q ρ h m h E m = E h, ρ m = ρ h, m m > m h ∴ K m i l d s t e e l K h i g h S t r e n g t h s t e e l = m m m h ≥ 1

(5)

4. 결 론

본 연구에서는 경량화를 위하여 자동차 차체부품을 일반강에서 고강도강소재로 치환함에 따라 경량화 부품의 강성에 어떠한 영향을 미치는지에 대한 검토를 수행하였다. 정강성 실험 및 해석결과, 인장강도 440 MPa, 두께 1.6 mm와 경량 고강도강 적용품인 인장강도 780 MPa, 두께 1.2 mm인 크로스멤버 강성은 각각 1,424 N/mm, 942 N/mm이며, 고유진동수 주파수 범위와 강성 간의 비례관계인 동강성 실험 및 해석의 1st mode 고유진동수 범위는 각각 44 Hz, 34 Hz 범위였다. 차체부품의 경량화 및 강도향상을 위한 고강도강의 적용 시 형상이 동일한 조건에서는 일반강에서 두께감소를 통한 경량화 고강도강으로 치환 시 강성은 감소함을 알 수 있었다. 이는 강재의 경우, 강성에 영향을 미치는 인자인 탄성계수, 밀도값의 변화없이 경량화를 위한 소재의 두께가 얇아짐에 따라 그만큼의 강성이 감소한 결과로 볼 수 있다.

따라서 동일한 형상으로 일반강재에서 두께가 감소한 경량화된 고강도강 소재로의 치환에 따른 차체부품의 강성의 향상은 어려우며, 경량화와 동시에 형상 최적화를 통해 차량이 요구하는 강성 확보가 가능할 것으로 판단된다.

또한 단위 차체부품 상태가 아닌 모듈화된 부품의 관계에서 강성의 향상은 접합부 성능향상 및 차체부품 요구하는 성능인자 파악을 통해 적재적소에 배치함으로써 가능할 것이다.

Nomenclature


A :	mass, Kg
B :	area, mm²
C :	natural frequency, Hz
D :	density, kg/m³
E :	stiffness, N/mm
F :	force, N
G :	displacement, mm
H :	constant
I :	modulus of elasticity, GPa
J :	moment of inertia, mm⁴

Subscripts


DOF :	degree of freedom

Acknowledgments

본 연구는 산업통상자원부와 한국산업기술진흥원이 지원하는 경제협력권산업 육성사업으로 수행된 연구결과입니다(A0128 00158).

References

R. Koehr, “Ulsac-lightweight Steel Automotive Closures”, SAE 2001-01-0076, (2001). [https://doi.org/10.4271/2001-01-0076]
Y. Li, Z. Lin, A. Jiang, and G. Chen, “Use of High Strength Steel Sheet for Lightweight and Crashworthy Car Body”, Materials and Design, 24(2), p177-182, (2003). [https://doi.org/10.1016/s0261-3069(03)00021-9]
B. L. Choi, and S. J. Kang, “Stiffness and Fatigue Strength Anlaysis of Fuel Cell Vehicle Body Frame”, Transactions of KSAE, 19(4), p47-53, (2011).
H. J. Kim, H. Kim, J. S. Kim, Y. K. Kim, and Y. E. Seo, “A Study on Dynamic Stiffness of HVAC”, KSAE Spring Conference Proceedings, p1137-1143, (2015).
F. A. Michael, Material Selection in Mechanical Design, Chapter 5.2 The selection Strategy, 4th edn., Butterworth-Heinnemaann, Oxford, p106-124, (2010).
X. Cui, H. Zhang, S. Wang, L. Zhang, and J. Ko., “Design of Lightweight Multi-material Automotive Bodies Using New Material Performance Indices of Thin-walled Beams for the Material Selection with Crashworthiness Consideration”, Material & Design, 32(2), p815-821, (2011). [https://doi.org/10.1016/j.matdes.2010.07.018]
T. Filetin, “Bending Stiffness of Aluminium Foams”, Technical Sciences, 15, p103-112, (2012).
M. F. Ashby, H. Shercliff, and D. Cebon, Materials Engineering Science Processing and Design, Chapter 5.2 Standard Solution to Elastic Design, Butterworth-Heinnemaann, Oxford, p88, (2007).

Table 1

Material properties

	440 MPa Steel	780 MPa Steel
Density	7850 kgf/mm²	7850 kgf/mm²
Young’s modulus	207 GPa	207 GPa
Poisson’s ratio	0.3	0.3
Yield stress	286.4 MPa	468.4 MPa

Table 2

Specific stiffness correlation according to shape type

Shape type	Specific stiffness	Specific strength	Remarks
Panel, Beam tensile	$E ρ$	$σ f ρ$	fix length / area changeable
Panel bending	$E 1 / 3 ρ$	$σ f 1 / 2 ρ$	fix length / fix width / thickness-changeable
Beam bending	$E 1 / 2 ρ$	$σ f 2 / 3 ρ$	fix length / area changeable
Beam torsion	$G 1 / 2 ρ$	$σ f 2 / 3 ρ$	fix length / area changeable