차량용 리튬이온 배터리 모듈의 간접 공랭식 시스템 냉각 특성 분석

1. 서 론

전 세계 자동차 생산 업체는 에너지 고갈과 환경문제로 인해 강화되고 있는 연비와 배기가스 규제에 대응하고 있다. 이에 따라 하이브리드 자동차(HEV: Hybrid Electric Vehicle), 플러그인 하이브리드 자동차(PHEV: Plug-in Hybrid Electric Vehicle), 전기 자동차(EV: Electric Vehicle)와 같은 친환경 자동차에 대한 연구가 활발히 진행되고 있다.^1-4) 이러한 친환경 자동차는 기존의 내연 기관 자동차보다 동력의 상당 부분을 배터리의 전기 에너지를 쓴다. 따라서 배터리의 용량이 커야 하기 때문에 배터리 시스템 탑재 용량은 하이브리드 차량은 1~2 kWh, 플러그인 하이브리드 차량은 4~16 kWh, 전기자동차는 20~100 kWh로 설계된다. 또한, 기존 내연기관 차량에서 사용하던 납축전지를 대신하여 에너지밀도가 높은 리튬이온 전지, 니켈수소 전지 등의 배터리가 사용된다. 특히, 리튬이온 전지는 출력 전압과 에너지 밀도가 높고 충･방전 특성이 우수하며, 수명이 길고 자가 방전율이 낮기 때문에 HEV/EV 등에서 많이 사용된다.^5-7)

차량용 리튬이온 배터리는 팩 단위로 사용되며, 팩 내 셀들의 평균온도를 적절히 유지하고, 셀 간 온도편차를 줄이는 것이 중요하다. 충･방전 시, 배터리를 적절한 온도로 유지하지 못하면 높은 온도로 인한 화재 및 폭발할 가능성이 있기 때문이다. 그뿐만 아니라 전기 화학 반응, 충･방전 효율, 전하 수용성 등에 악영향을 끼치며 결국에는 배터리 수명을 감소시킨다.^8-10) 또한, 셀 간 온도편차로 인해 셀 간 내부저항의 불균형이 생기면 사용 가능한 배터리 셀이 많이 남아있음에도 불구하고, 배터리 모듈을 교체해야하는 문제가 발생한다. 따라서 다양한 운전조건과 과도적인 출력 상황에서도 배터리를 적절한 온도로 유지하며, 셀 간 온도편차를 줄일 수 있는 배터리 냉각시스템이 필요하다.⁴⁾

배터리 냉각은 냉각 유체를 이용하며, 수랭식과 공랭식이 있다. 수랭식의 경우, 배터리의 발열량이 큰 경우에 사용된다. 냉각수의 열용량이 크기 때문에 냉각성능이 우수하지만, 냉각 유로를 설치해야 하는 부담이 있다. 반면에 공랭식의 경우, A/C 칠러를 통해 냉각된 공기나 외기 공기를 사용한다. 공랭식은 수랭식보다 시스템이 비교적 단순하며, 생산단가가 저렴하고 유지보수가 쉽다. 또한 공랭식에서 사용하는 공기는 열용량이 작아 온도를 쉽게 조절할 수 있다.⁴⁾

공랭식 배터리에 대한 다양한 연구가 진행되고 있다. 장호선 등¹¹⁾ 원통형 배터리 셀의 배열이 셀 간의 온도편차, 냉각성능, 냉각 유체 소모동력에 끼치는 영향을 연구하였다. 박성진 등¹²⁾은 배터리 셀 간의 온도편차를 최소화하기 위해 냉각 유체의 유동 방향을 시간에 따라 바꾸며 셀의 온도편차를 분석하였다. 백승기와 박성진¹³⁾은 알루미늄 냉각 판의 두께, 형태, 개수가 냉각성능에 중요 인자임을 확인하였다. Mohammadian 등¹⁴⁾은 하이브리드 자동차용 공랭식 배터리 팩의 Pin-fin 히트싱크의 배열, 공기 유량, 공기 온도가 배터리 냉각에 끼치는 영향을 연구하였다. Teng 등¹⁵⁾은 배터리 냉각용 알루미늄 판의 다양한 형태가 배터리 온도에 미치는 영향을 분석하였다. 또한, 냉각시스템은 성능, 조립, 무게, 부피효율을 고려하며 상호 간 최적의 설계를 하는 것이 중요하다.

본 연구에서는 각형 3원계 리튬이온 배터리(NMC) 셀로 구성된 PHEV용 배터리 팩의 하나의 모듈의 냉각시스템 모델을 개발하였다. 배터리 냉각 시스템은 간접 공랭식이고 MATLAB/Simulink 환경에서 1-D 모델로 개발하였다. 본 논문에서 개발된 1-D 모델은 CFD에 비해 신속하게 셀의 온도편차를 예측할 수 있다. 모델은 CFD 결과를 바탕으로 검증하였으며, 모델을 통해 냉각시스템 운전조건과 디자인 변화에 따른 셀의 최고･최저온도, 셀 간 최대 온도편차, 배터리 모듈의 온도분포 및 열전달률 등의 냉각특성을 비교분석 하였다.

2. 배터리 모듈 냉각 성능 예측 모델 개발

2.2 모델링 방법

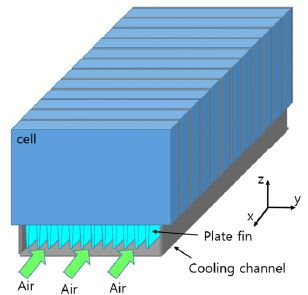
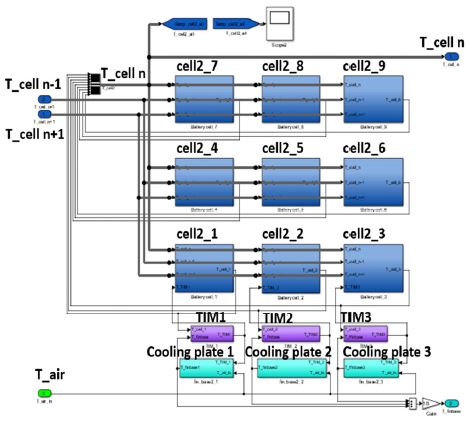
본 연구에서는 각형 3원계 리튬이온 배터리(NMC) 셀로 구성된 PHEV용 배터리 팩의 하나의 모듈의 냉각 시스템 모델을 개발하였다. Fig. 1은 연구대상인 간접 공랭식 배터리 모듈의 구조를 나타낸다. 모듈은 12개의 각형 셀로 구성되며, 셀 하단에는 냉각성능을 높이기 위한 핀형 공기 채널이 있다. 이 채널을 지나는 냉각공기가 대류와 전도를 통해 배터리를 방열시키는 구조이다.

Fig. 1

Schematic of indirect air cooling battery module

따라서 냉각 예측 모델은 배터리 셀, 냉각채널, 냉각공기로 구성된다. 배터리 모듈의 열 해석을 위해 연속체인 구조물을 유한개의 ‘요소’로 나누어 각기 영역에 대해 에너지 방정식을 통해 근사해를 구하는 방법인 유한요소법을 사용하였다. 따라서 배터리 모듈의 각 컴포넌트는 여러 개의 요소로 나뉘며 냉각공기도 그에 맞는 검사체적으로 나뉘어 에너지 방정식을 푸는 데 사용된다. 또한, 냉각 예측 모델은 기본적으로 배터리 모듈의 기하학적 수치나 각 컴포넌트의 밀도, 비열, 열전도도와 같은 물성치가 입력되어, 각 요소의 질량, 열전달 면적, 열저항 등이 에너지 방정식을 푸는 데 반영된다.

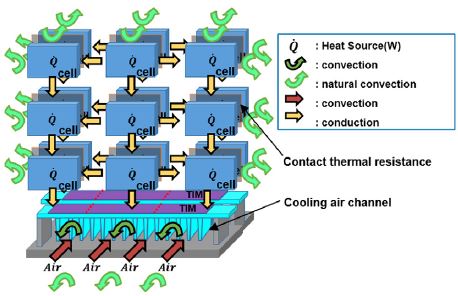
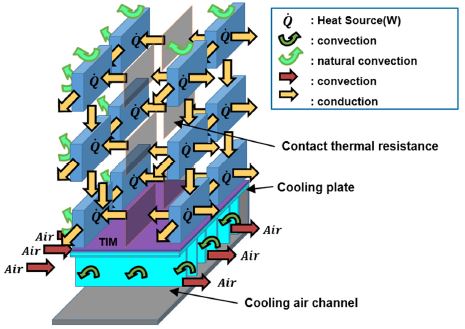
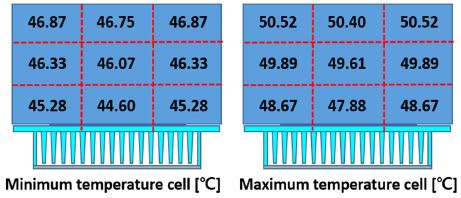
배터리 모듈의 열 해석을 위해 셀은 CFD 온도분포 결과를 토대로 하나의 셀을 Fig. 2와 같이 상하로 3개 좌우로 3개, 총 9개의 셀 요소(직육면체 형태)로 나누었으며, 셀 요소 내의 온도구배는 없다고 가정하였다. 셀 요소는 상, 하, 좌, 우, 앞, 뒤로 6방향의 열전달과 셀 자체의 내부 발열을 포함하여 Fig. 3, Fig. 4와 같이 총 7개의 열전달로 구성된다. 식 (1)은 분할된 셀 요소의 온도 변화를 나타내며 식 (2)는 셀 요소의 총 열전달률이다.

Fig. 2

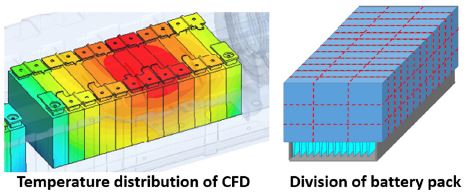
Temperature distribution of battery module in CFD and division of battery module for multi - dimensional heat transfer model

Fig. 3

Schematic of heat transfer of battery module (front view)

Fig. 4

Schematic of heat transfer of battery module (side view)

$\[ \frac{d{T}_{cell}}{dt}=\frac{{\dot{Q}}_{total}}{m_{cell}C{p}_{cell}} \]$

(1)

$\[ {\dot{Q}}_{total}={\dot{Q}}_{cell,heat}+{\dot{Q}}_{front}+{\dot{Q}}_{back}+{\dot{Q}}_{left}+{\dot{Q}}_{right}+{\dot{Q}}_{up}+{\dot{Q}}_{down} \]$

(2)

여기서, $$ {\dot{Q}}_{total}$$은 셀 요소의 총 열전달률, m_cell은 셀 요소의 질량, Cp_cell은 셀의 비열이다. $$ {\dot{Q}}_{cell,heat}$$은 셀 요소의 발열량이며, 발열이 셀 전체에 골고루 퍼져있다고 가정하여 셀 당 발열량을 해당하는 부피만큼 나눠 계산된다. $$ {\dot{Q}}_{front}$$, $$ {\dot{Q}}_{back}$$, $$ {\dot{Q}}_{left}$$, $$ {\dot{Q}}_{right}$$, $$ {\dot{Q}}_{up}$$, $$ {\dot{Q}}_{down}$$은 셀 요소의 앞, 뒤, 좌, 우, 위, 아래 방향 열전달률을 나타낸다. 분할된 셀의 위치에 따라 하나의 셀 내부에서 분할된 셀 요소 간의 전도, 이웃한 셀 간의 전도, TIM(Thermal interface material)과의 전도, 외기와의 자연대류 열전달로 구성된다. 배터리 셀과 외기의 자연대류 열전달률은 식 (3)과 같으며, 배터리 셀 요소 사이의 전도 열전달률은 식 (4)와 같이 나타낸다.

$\[ {\dot{Q}}_{conv,natural}=h_{natural}A\left(T_{ambi}-T_{cell}\right) \]$

(3)

$\[ {\dot{Q}}_{cond}=\frac{\left(T_{cell,1}-T_{cell,2}\right)}{R_{total}} \]$

(4)

여기서, $$ {\dot{Q}}_{conv,natural}$$은 셀과 외기의 자연대류 열전달률이며, h_natural은 자연대류 열전달계수, A는 외기와 셀의 열전달 면적, T_ambi는 외기온도, T_cell은 셀 요소의 온도이다. $$ {\dot{Q}}_{cond}$$는 셀 요소 사이의 전도 열전달률, T_cell,1과 T_cell,2는 각 셀 요소의 온도, R_total은 총 합 열저항이다.

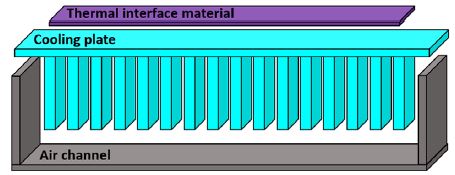
냉각채널은 Fig. 5와 같이 TIM, 냉각판(Cooling plate), 공기채널(Air channel)로 구성된다. TIM은 열전달 물질로 셀과 냉각판의 접촉 열 저항을 최소화하는 역할을 하며 위쪽 셀과 아래쪽 냉각판과 전도열전달을 한다. 냉각판에는 열전달 효율을 증가하기 위한 냉각핀이 있다.

Fig. 5

Schematic of cooling channel of battery module

냉각공기를 통한 열전달률은 채널 형상, 운전조건 등에 따라 누셀트수(Nusselt number)와 대류 열전달 계수 등을 통해 계산된다. 먼저, 식 (5)는 냉각공기의 레이놀즈수(Reynolds number)를 나타낸다.

$\[ Re=\frac{\rho V{D}_h}{\mu } \]$

(5)

여기서, ρ는 냉각공기의 밀도, V는 냉각공기의 유속, D_h는 냉각채널의 수력지름이며, μ는 냉각공기의 점성계수를 나타낸다.

누셀트수는, 냉각공기가 층류일 때는 일정 표면 온도, 완전발달 조건으로 가정하여 상수인 3.66을 사용했으며,¹⁶⁾ 난류일 때는 Dittus-Boelter의 상관식인¹⁷⁾ 식 (6)으로 계산된다. Nu는 냉각공기의 누셀트 수 이며, Pr은 냉각공기의 프란틀수이다.

$\[ Nu=0.023R{e}^{4/5}\text{P}{\text{r}}^{\text{0.3}} \]$

(6)

h는 대류 열전달 계수로 식 (7)과 같이 계산되며 k는 냉각핀의 열전도도이다.

$\[ Nu\equiv \frac{h{D}_h}{k} \]$

(7)

냉각핀의 대류열전달은 식 (8)과 (9)를 이용하여 계산한다.

$\[ h\theta \left(L\right)=-{kd\theta ∕dx|}_{x=L} \]$

(8)

$\[ {\dot{q}}_{fin}=M\frac{\sinh mL+\left(h/mk\right)\cosh mL}{\cosh mL+\left(h/mk\right)\sinh mL} \]$

(9)

여기서, θ는 초과온도, P는 접수 길이, A_c는 핀의 단면적, m과 M은 식 (10), 식 (11)과 같다.

$\[ m^2\equiv hP/k{A}_c \]$

(10)

$\[ M\equiv \sqrt{hPk{A}_c}{\theta }_b \]$

(11)

또한, 채널에 흐르는 냉각공기는 각 검사 체적을 지나며 에너지 방정식을 통해 온도가 계산된다. 냉각공기의 총 열전달률을 $$ {\dot{Q}}_{air,total}$$이라고 하면 검사 체적을 지나는 냉각공기는 식 (12)와 같은 에너지 방정식을 성립한다.

$\[ {\dot{m}}_{air}C{p}_{air}\left(T_{air,out}-T_{in,air}\right)={\dot{Q}}_{air,total} \]$

(12)

여기서, $$ {\dot{m}}_{air}$$은 냉각공기 질량유량, Cp_air는 냉각공기 비열, T_air,out, T_air,in는 검사체적 출구, 입구의 냉각공기 온도이다.

또한, 채널을 지나는 냉각공기의 압력강하는 식 (13)을 이용하여 계산한다.

$\[ ∆P=f\frac{l}{D_h}\frac{\rho V^2}{2} \]$

(13)

여기서, f는 유체의 점성에 의한 마찰계수로 냉각공기가 층류일 때는 식 (14)로 계산되고, 난류일 때는 식 (15)와 같은 Haaland의 식으로 계산된다.¹⁸⁾ l은 채널의 길이, ε는 표면 거칠기를 나타낸다.

$\[ f=\frac{64}{Re} \]$

(14)

$\[ \frac{1}{\sqrt{f}}=-1.8\log \left[{\left(\frac{\epsilon {/D}_h}{3.7}\right)}^{1.11}+\frac{6.9}{Re}\right] \]$

(15)

위와 같은 열전달과 유체역학 식을 바탕으로 배터리 모듈 냉각성능 예측모델을 Matlab/Simulink를 이용해 구현하였다. Fig. 6은 배터리 모듈의 Matlab/Simulink 모델로 12개의 셀 블록과 12개의 검사체적을 갖는 냉각공기 블록, 대류열전달계수 계산 블록으로 구성된다. Fig. 7은 9개의 요소로 분할된 셀과 각 3개의 요소로 분할된 TIM, 냉각판의 블록이다. 각 컴포넌트의 온도, 열전달률 등은 Time step마다 각각의 블록이 온도나 유량 등의 정보를 주고받으며 계산된다.

Fig. 6

Heat transfer model of indirect air cooling battery module in Matlab/Simulink

Fig. 7

Heat transfer model of Cell, TIM, Cooling plate in Matlab/Simulink

2.3 모델 검증

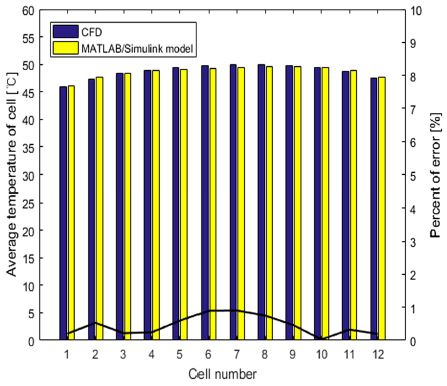
모델 검증은 정상상태를 기준으로 CFD 결과와 MATLAB/Simulink 모델의 결과를 비교하였다. 배터리 사양 및 냉각판의 재질은 Table 1과 같으며 검증 시뮬레이션 조건은 Table 2와 같다. Fig. 8은 CFD와 MATLAB/Simulink 모델의 12개 셀 온도와 오차율을 나타내며 오차율은 1 % 이내이다.

Table 1

Specification of cell and cooling plate

Table 2

Condition of simulation (case 1)

Fig. 8

Comparison of battery cell temperature between CFD model and MATLAB/Simulink model in case 1

Fig. 9와 같이, 배터리의 열전달은 크게 3가지이며 셀의 발열, 셀과 외기의 자연대류열전달, 셀과 TIM의 전도 열전달로 구분된다. 여기서 간접 공랭식 배터리 모듈의 셀과 냉각공기사이에 열전달은 TIM을 통해 이루어진다. Table 3은 배터리 모듈 내 셀의 총 발열량, 배터리 모듈에서 냉각공기로의 총 열전달률, 배터리 모듈에서 외기로의 총 열전달률을 나타낸다. 셀의 총 발열량은 39.3 W이며 그 중 35.8 W는 냉각공기로, 3.5 W는 외기를 통해 냉각된다. 즉 배터리 모듈을 냉각시키는 열전달 중 91 % 이상이 냉각공기를 통해 이뤄진다. Fig. 10은 12개 셀 중 최저온도인 첫 번째 셀과 최고온도인 아홉 번째 셀의 온도 분포이다. Fig. 10에서 볼 수 있듯이, 냉각공기와 가까운 셀 요소는 상대적으로 낮은 온도이다.

Fig. 9

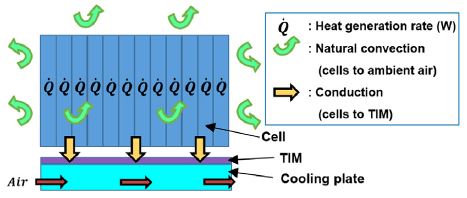
Schematic of heat generation rate of cells, natural convection heat transfer and conduction heat transfer between cells and TIM

Table 3

Heat transfer of cells and pressure drop of cooling air in case 1

Fig. 10

Temperature distribution of maximum and minimum temperature cells in battery module

3. 시뮬레이션 및 결과

시뮬레이션은 Table 4를 기본 조건으로 하여 외기 온도, 전류, 냉각공기 유량, 냉각공기 온도 및 냉각핀 개수를 변경하며 진행하였다. 각 값의 변경범위는 Table 5와 같다.

또한, 시뮬레이션을 통해 정상상태에서 배터리 모듈 내의 최고･최저 셀 온도, 셀 간 최대 온도편차 등을 분석하였다. 본 연구에서, 하나의 셀 온도는 9개로 나뉜 셀 요소들의 평균온도로 사용했으며, 셀 간 최대 온도편차는 모듈 내 최고･최저온도의 셀의 온도차이이다. 또한 전류는 셀 당 흐르는 전류의 크기이다.

3.1 운전 조건의 영향

3.1.1 외기온에 따른 영향

Table 4와 같은 기본 조건에서 외기온을 30 °C에서 55 °C까지 변경하며 시뮬레이션 한 결과를 Fig. 11에 나타냈다. Fig. 11(a)는 외기온에 따른 배터리 모듈 내의 최고･최저 셀 온도, 셀 간 최대 온도편차이며, Fig. 11(b)는 12개 셀의 총 발열량, 셀의 냉각공기와 외기로의 열전달률이다. 외기온도가 높을수록 셀의 최고･최저 온도가 높아진다. 이는 Fig. 11(b)와 같이 외기온이 높을수록 셀에서 외기로의 열전달률이 줄어들며, 외기온이 50 °C 이상이 되면 오히려 외기에서 셀로 열전달이 생기기 때문이다.

Table 4

Base condition of simulation

Table 5

Value range of various parameters

Fig. 11

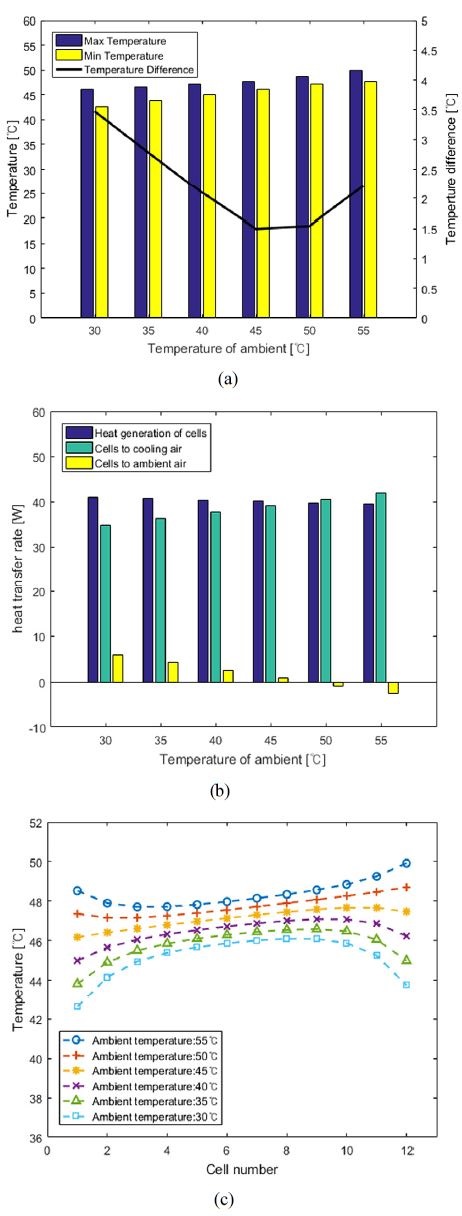
Simulation result according to ambient temperature (Current:60 A) (a) Maximum, minimum temperature and maximum temperature difference of cells, (b) Heat transfer rate of total cells, (c) Temperature of each cell in battery module

또한, 셀 간 최대 온도편차도 외기온에 영향을 받는다. 냉각공기가 30 °C, 60 CMH이고 전류가 60 A인 기본 조건에서 모듈의 가운데 셀의 온도는 외기온에 따라 45~48 °C 수준으로 나타난다. 반면, 자연 대류 열전달 면적이 넓은 첫 번째, 마지막 셀은 외기의 영향을 많이 받아, 외기온에 따라 43~49 °C의 온도를 갖는다. 따라서 외기온이 30 °C 혹은 55 °C일 때 Fig. 11(c)와 같이 셀의 온도분포가 위로 볼록하거나 아래로 오목한 형태를 띠며 셀 간 온도편차가 커진다.

Fig. 12(a)는 전류가 30 A일 때 외기온도에 따른 시뮬레이션 결과이다. 낮은 전류로 인해 Fig. 12(b)와 같이 셀의 발열량이 줄어 전류 60 A 조건보다 최고･최저 셀 온도가 낮다. 또한, 60 A 조건과는 다르게 셀 간 최고온도편차는 외기온도가 35 °C일 때 가장 작아진다. 그 이유는 전류 30 A 조건에서 외기온도가 35 °C일 때 셀의 외기로 방열량이 최저가 되어 12개셀의 온도 분포가 Fig. 12(c)와 같이 균일해지기 때문이다.

Fig. 12

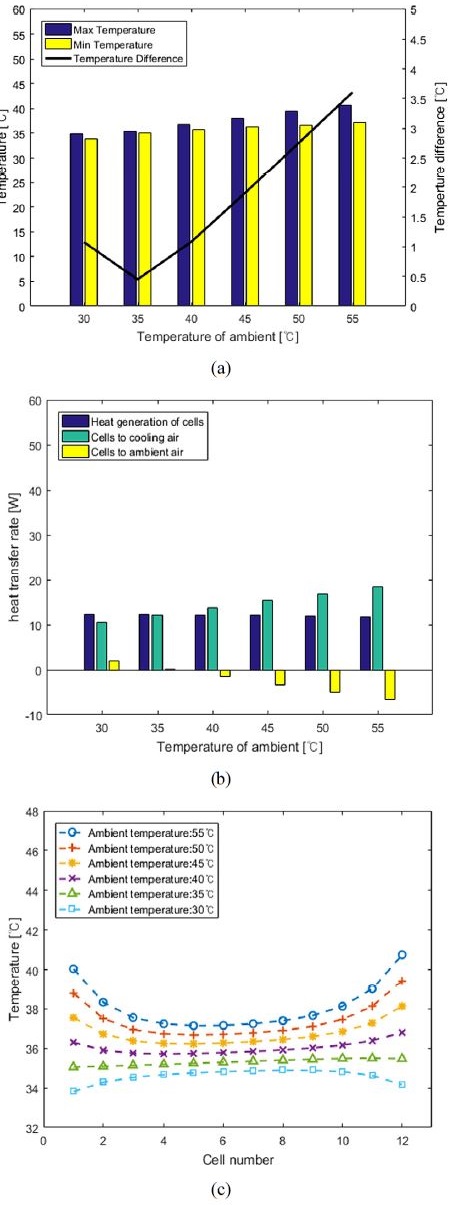
Simulation result according to ambient temperature (Current:30 A) (a) Maximum, minimum temperature and maximum temperature difference of cells, (b) Heat transfer rate of total cells, (c) Temperature of each cell in battery module

외기온도가 높을수록 셀 온도가 증가한다. 또한, 외기온도와 셀의 온도 차이에 따라 배터리 모듈 내 셀의 온도분포가 결정되며 차이가 작을수록 셀 간 최대 온도편차는 줄어든다.

3.1.2 전류(발열량)에 따른 영향

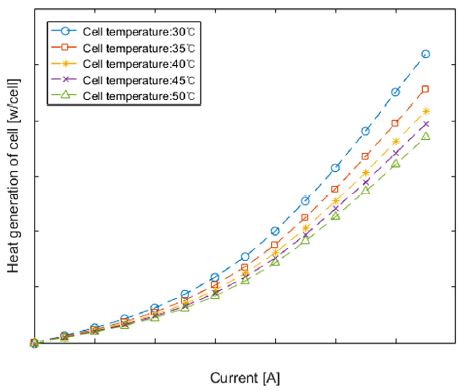
배터리 셀의 발열량은 전류와 셀 온도에 따른 맵데이터를 사용하였다. Fig. 13은 전류 크기와 셀 온도에 따른 셀의 발열량을 나타낸다. 셀의 발열량은 전류의 제곱에 비례하며, 셀 온도가 낮을수록 셀의 내부저항이 높아져서 발열량이 증가한다. Table 4와 같은 기본 조건에서 전류를 0 A ~ 80 A로 변경하며 시뮬레이션 한 결과는 Fig. 14와 같다. 전류에 따른 배터리 모듈 내의 최고･최저 셀 온도, 셀 간 최대 온도편차는 Fig. 14(a)이며, Fig. 14(b)는 12개 셀의 총 발열량, 셀의 냉각공기와 외기로의 열전달률이다. Fig. 14(b)와 같이 전류가 증가할수록 발열량이 전류의 제곱에 비례하여 증가하므로 Fig. 14(a)와 같이 최고 셀 온도, 최저 셀 온도가 증가한다. 또한, 셀의 온도 증가로 인해 셀과 냉각공기의 온도차이가 커져 셀에서 냉각공기로의 열전달률도 증가한다. 셀에서 외기로의 열전달은 Fig. 14(b)와 같이 셀 온도가 외기온도(45 °C)보다 낮으면 외기에서 셀로 열전달, 높으면 셀에서 외기로 열전달이 된다. 50 A 조건일 때, 셀에서 외기로의 방열량은 최소가 되어 Fig. 14(c)와 같이 12개 셀은 균일한 온도 분포를 갖기 때문에 셀 간 최대 온도편차가 최소가 된다.

Fig. 13

Heat generation of cell according to current and temperature of cell

Fig. 14

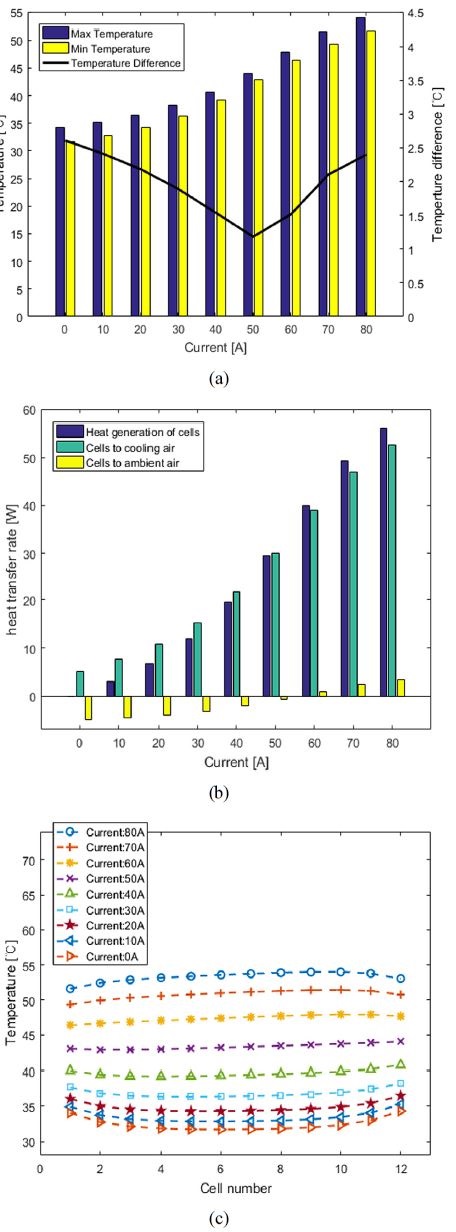
Simulation result according to current (a) Maximum, minimum temperature and maximum temperature difference of cells, (b) Heat transfer rate of total cells, (c) Temperature of each cell in battery module

셀의 발열량은 전류, 셀 온도와 관계되며 전류의 제곱에 비례한다. Table 4와 같은 기본조건에서 전류가 0 A ~ 80 A가 되면 12개의 셀의 총 발열량은 0 W ~ 56 W가 된다. 또한, 셀의 발열량과 셀 온도는 선형적으로 비례한다.

3.1.3 냉각공기 유량에 따른 영향

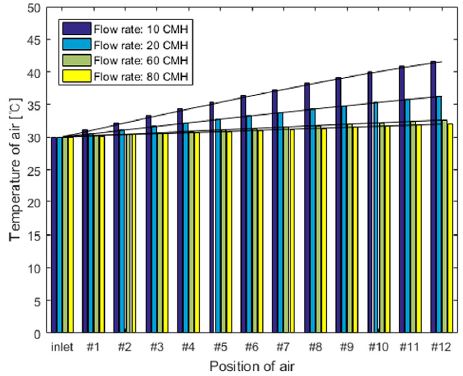
Table 4와 같은 기본 조건에서 냉각공기의 유량을 10 CMH ~ 100 CMH로 변경하며 시뮬레이션 한 결과는 Fig. 15, Fig. 16과 같다. Fig. 15는 셀 밑을 지나는 냉각공기의 온도를 나타낸다. 냉각공기의 유량에 따른 배터리 모듈 내의 최고･최저 셀 온도, 셀 간 최대 온도편차는 Fig. 16(a)와 같다. 유량이 증가함에 따라 셀의 최고･최저 온도가 줄어드는 것을 알 수 있다. 이는 크게 두 가지 영향으로 나눌 수 있다. 첫째, 유량이 적으면 레이놀즈수가 작은 층류영역에 속하여 누셀트수가 상수로 일정해 대류 열전달 계수가 난류에 비해 낮다. 반면에 레이놀즈수가 높으면 냉각공기는 난류유동을 형성하여 누셀트수가 레이놀즈수와 비례한다. 따라서 대류 열전달 계수가 층류 유동에 비해 커져 냉각성능이 향상한다. 둘째로 냉각공기의 유량이 많아질수록 냉각공기의 열용량이 커져, Fig. 15와 같이 냉각공기가 채널을 지나며 셀을 냉각해도 냉각공기의 온도 변화가 작아진다. 따라서 첫 번째 셀부터 마지막 셀을 냉각시킬 때까지 냉각성능을 유지할 수 있다. 반면에 유량이 적은 조건(10 CMH)에서는 냉각공기가 채널을 지나며 온도가 높아져 Fig. 16(c)와 같이 뒤쪽 셀은 충분히 냉각되지 못한다. 따라서 모듈 내 셀 간 온도편차를 줄이기 위해, 첫 번째 셀부터 마지막 셀까지 일정하게 냉각할 수 있을 만큼의 냉각공기 유량이 필요하다.

Fig. 15

Temperature of cooling air under the cells according to flow rate of cooling air

Fig. 16

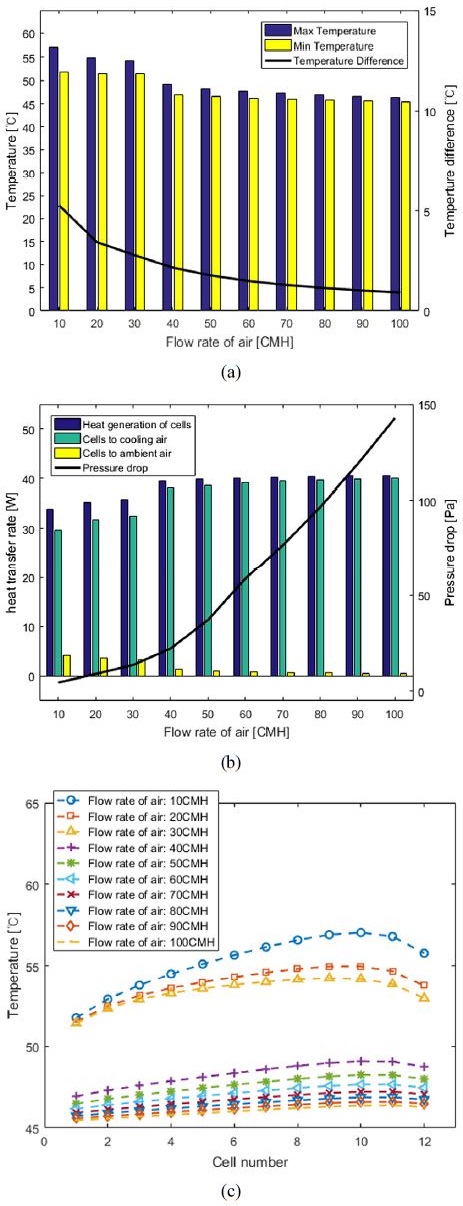
Simulation result according to flow rate of cooling air (a) Maximum, minimum temperature and maximum temperature difference of cells, (b) Heat transfer rate of total cells and pressure drop of cooling air, (c) Temperature of each cell in battery module

Fig. 16(b)는 셀의 발열량과 배터리 셀의 냉각공기와 외기로의 열전달률 그리고 채널을 지나는 냉각공기와 외기로의 열전달률 그리고 채널을 지나는 냉각공기의 압력강하를 나타낸다. 냉각공기의 유량이 낮을 때 전류가 60 A임에도 불구하고 배터리의 발열량이 낮다. 그 이유는 냉각공기의 유량이 적을 때 셀의 온도가 높아지며 셀의 내부저항이 낮아져 발열량이 줄어들기 때문이다.

또한, Fig. 16(b)와 같이 셀에서 냉각공기로의 열전달률은 일정 유량 이상이 되면 거의 일정하지만 냉각공기의 유량이 증가할수록 압력강하는 유량의 제곱에 비례하며 증가한다.

3.1.4 냉각공기 온도에 따른 영향

Table 4와 같은 기본 조건에서 냉각공기의 온도를 10 °C ~ 45 °C로 변경하며 시뮬레이션한 결과는 Fig. 17과 같다. Fig. 17(a)는 냉각공기의 온도에 따른 배터리 모듈 내의 최고･최저 셀 온도, 셀 간 최대 온도편차이다. 냉각공기 온도가 높아지면 셀의 최고･최저 온도가 선형적으로 증가함을 나타낸다. 그 이유는 냉각공기의 온도가 높아질수록 냉각공기와 셀의 온도 차이가 작아져 Fig. 17(b)와 같이 냉각공기를 통한 대류 열전달률이 줄어들기 때문이다. 셀에서 냉각공기로의 열전달률은 냉각공기의 온도가 10 °C 일 때 54 W, 45 °C일 때 27 W이다.

Fig. 17

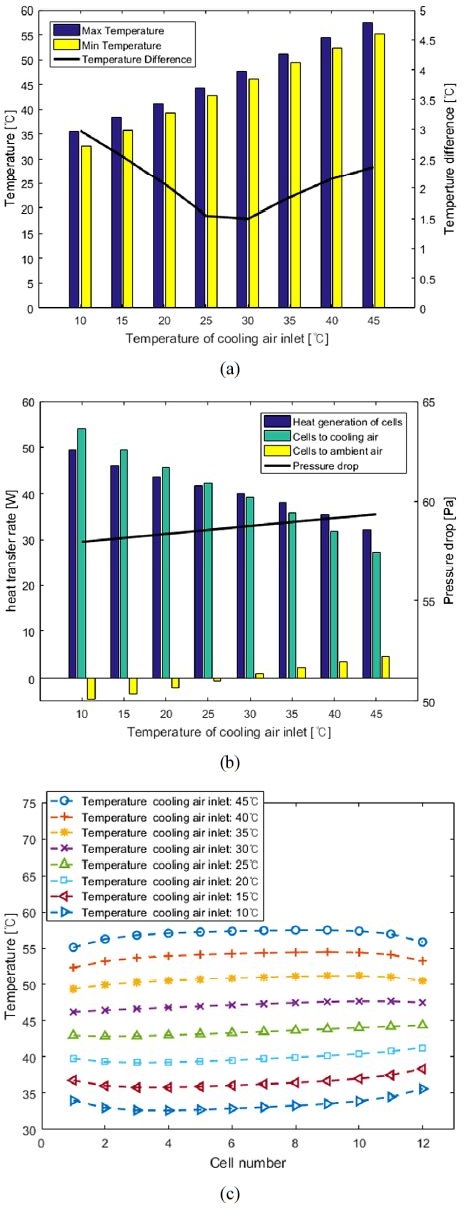
Simulation result according to temperature of cooling air inlet (a) Maximum, minimum temperature and maximum temperature difference of cells, (b) Heat transfer rate of total cells and pressure drop of cooling air, (c) Temperature of each cell in battery module

또한, 냉각공기 온도가 높을수록 셀 온도가 증가하며 전체 셀의 온도가 외기온도(45 °C)보다 낮을 때는 외기에서 셀로 열전달, 외기온도(45 °C)보다 높을 때는 셀에서 외기로 열전달된다. 또한, 냉각공기의 온도가 25 °C ~ 30 °C 일 때 셀과 외기의 온도차이가 최소가 되어 외기의 영향이 가장 작아진다. 이 때 Fig. 17(c)와 같이 12개 셀은 균일한 온도 분포를 띄며 셀 간 최대 온도편차가 최소가 된다.

냉각공기의 온도가 낮을 때 전류가 60 A임에도 불구하고 배터리의 발열량이 높다. 그 이유는 냉각공기의 온도가 낮을 때 셀의 온도가 낮아, 셀의 내부저항이 높아져 발열량이 증가하기 때문이다.

Fig. 17(b)와 같이 냉각공기의 온도가 10 °C ~ 45 °C로 증가할수록 채널을 지나는 공기의 압력강하는 2 Pa 증가한다. 공기의 온도가 증가하면 공기의 점성계수 μ가 커져서 마찰계수가 증가하기 때문이다.

3.2 냉각핀 개수의 영향

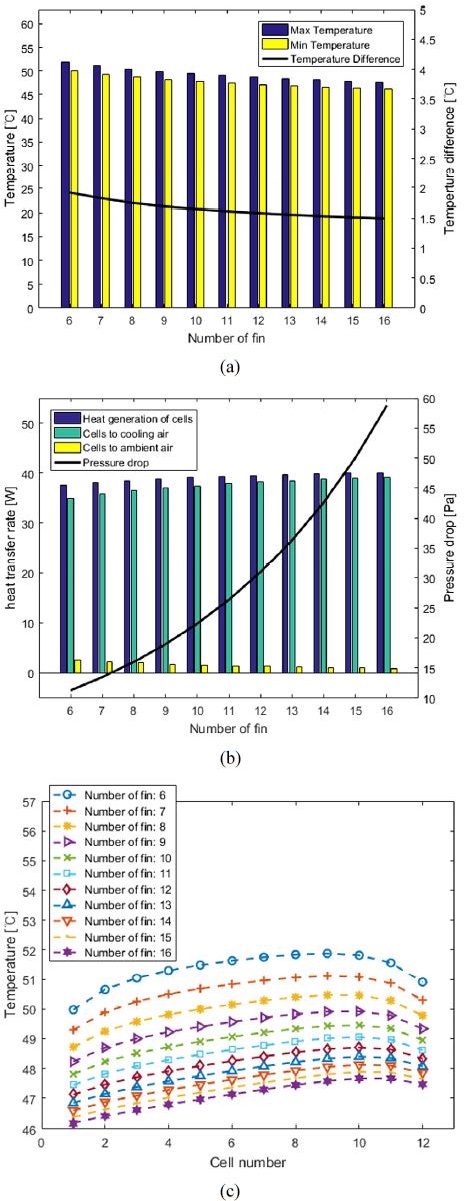
Table 4와 같은 기본 조건에서 냉각채널의 냉각핀 개수를 6개에서 16개로 변경하며 시뮬레이션 한 결과는 Fig. 18과 같다. 냉각핀 개수에 따른 배터리 모듈 내의 최고･최저 셀 온도, 셀 간 최대 온도편차는 Fig. 18(a)과 같으며 Fig. 18(b)은 셀의 발열량과 배터리 셀의 냉각공기와 외기로의 열전달률 그리고 채널을 지나는 냉각공기의 압력강하를 나타낸다. 냉각핀의 개수가 증가함에 따라 최고･최저 셀 온도가 줄어든다. 이는 냉각핀의 수가 증가함에 따라 냉각공기와 대류가 일어나는 열전달 면적이 증가해, 대류 열전달률이 증가하기 때문이다. 또한, 냉각공기의 유량이 일정하고 냉각채널의 단면적이 일정할 때 핀의 개수가 늘면 실제 공기가 지나는 단면적이 줄어, 공기의 유속이 커져 대류 열전달계수가 커지기 때문이다. 하지만 냉각핀의 개수가 많아질수록 냉각공기로 빠져나가는 열전달률의 증가 폭은 줄어든다. 반면에 냉각공기의 압력강하는 유속의 제곱에 비례하며 늘어난다. 따라서 냉각유체를 구동하기 위한 소모동력이 증가한다. 또한, 냉각핀 개수가 증가하면 배터리 모듈의 무게, 가격도 증가한다. 따라서 냉각성능과 소모동력, 무게, 가격 등을 고려하여 냉각핀의 개수를 선정해야 한다.

Fig. 18

Simulation result according to number of fin (a) Maximum, minimum temperature and maximum temperature difference of cells, (b) Heat transfer rate of total cells and pressure drop of cooling air, (c) Temperature of each cell in battery module

3.3 운전 조건에 따른 배터리 모듈 내의 최고 셀 온도, 셀 간 최대 온도편차

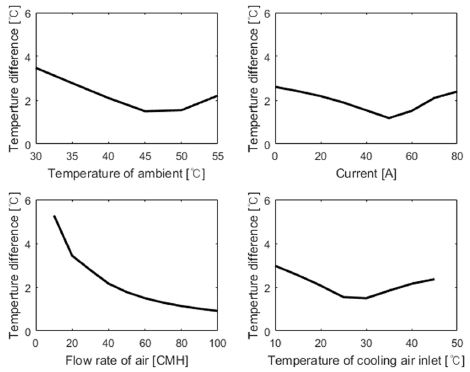
다양한 운전 조건에서 배터리 모듈 내의 최고 셀 온도는 Fig. 19와 같다. 셀의 최고 온도는 외기온도, 전류, 냉각공기 온도에 비례하며, 외기온도보다 전류, 냉각공기 온도에 더 민감하게 변화된다. 한편 냉각공기 유량이 많을수록 최고 셀 온도가 감소하며, 특히 유량이 40 CMH 이상이 되면 냉각공기의 유동은 난류가 되어 냉각공기를 통한 셀의 냉각량이 증가하고 최고 셀 온도가 낮아진다.

Fig. 19

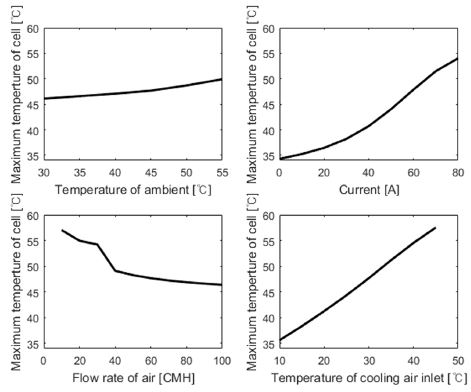
Maximum temperature of cells in battery module under various conditions (temperature of ambient, current, flow rate of air and temperature of cooling air inlet)

다양한 운전 조건에서 배터리 모듈 내의 셀 간 최대 온도편차는 Fig. 20과 같다. 셀 간 온도편차는 냉각공기의 유량이 많을수록 줄어든다. 유량이 많아지면, 채널을 지나는 냉각공기의 온도 증가량이 적어, 모듈 내의 뒤쪽 셀까지 충분히 냉각할 수 있다. 따라서 앞, 뒤 셀 온도편차가 줄어 셀 간 최대 온도편차가 줄어든다. 또한, 셀과 외기의 자연대류 열전달에 의한 셀 간 온도편차가 존재하는데 이는 모듈 내에서 셀의 위치에 따라 외기와의 열전달 면적이 다르기 때문이다. 첫 번째 셀과 마지막 셀은 외기와의 열전달 면적이 크기 때문에, 외기와 온도 차이가 크면 열전달률이 커져서 전체 셀의 평균 온도와 차이가 커지게 된다. 따라서 Fig. 20과 같이 다양한 조건에서 온도편차가 최저가 되는 지점이 존재하며, 이는 셀의 전체적인 온도와 외기온도 차이가 최소가 되는 운전조건이다.

Fig. 20

Maximum temperature difference of cells in battery module under various conditions (temperature of ambient, current, flow rate of air and temperature of cooling air inlet)

4. 결 론

본 논문에서는 MATLAB/Simulink를 이용해 각형셀로 구성된 간접 공랭식 리튬이온 배터리 모듈의 냉각 예측 모델을 구성하고 CFD 시뮬레이션 결과와 비교를 통해 검증하였다. 그 후 MATLAB/Simulink 모델을 이용해 다양한 운전조건이나 설계요소에 따른 배터리 모듈 냉각특성을 비교분석 하였다. 이를 통해 간접 공랭식 배터리 냉각시스템의 특성에 대해 다음과 같은 결론을 내릴 수 있었다.

• 1) 외기온도가 높을수록 셀에서 외기로의 방열량이 줄어들어 셀의 최고･최저 온도가 증가한다.
• 2) 외기온도와 셀의 온도 차이에 따라 배터리 모듈 내 셀의 온도분포가 결정되며, 셀과 외기온도 차이가 작을수록 배터리 모듈 내 셀 간 최대 온도편차는 줄어든다.
• 3) 냉각핀의 개수가 늘어나면 열전달 면적이 커져 열전달률이 증가하지만, 냉각 유체의 유량이 일정할 때 냉각 유체 통로 단면적이 줄어들어 압력강하가 커진다.
• 4) 배터리 모듈 내의 최고 셀 온도는 외기온도, 전류, 냉각공기 온도에 비례하며 냉각공기의 유량이 증가하면 감소한다.

Acknowledgments

본 연구는 방위사업청과 국방과학연구소의 지원으로 수행되었습니다(계약번호 : UC150014ID).

References

• J. H. Lee, K. H. Lee, and J. H. Choi, “Design of Charge and Discharge Monitoring System for Secondary Batteries of Hybrid Electric Vehicle”, Journal of the Korea Society of Computer and Information, 15(8), p157-161, (2010). [https://doi.org/10.9708/jksci.2010.15.8.157]
• S. E. Yoo, and D. H. Shin, “Electric Vehicle Market and Technology Trend”, Auto Journal, KSAE, 32(8), p22-27, (2010).
• Q. Wang, Z. Rao, Y. Huo, and S. Wang, “Thermal Performance of Phase Change Material/Oscillating Heat Pipe-based Battery Thermal Management System”, International Journal of Thermal Sciences, 102, p9-16, (2016). [https://doi.org/10.1016/j.ijthermalsci.2015.11.005]
• T. W. Kim, and S. J. Park, “Battery Thermal Management System for Electric Vehicles”, Magazine of the SAREK, 44(11), p28-38, (2015).
• M. Wakihara, “Recent Developments in Lithium Ion Batteries”, Materials Science and Engineering, 33(4), p109-134, (2001).
• K. Zaghib, M. Dontigny, A. Guerfi, P. Charest, I. Rodrigues, A. Mauger, and C. M. Julien, “Safe and Fast-charging Li-ion Battery with Long Shelf Life for Power Applications”, Journal of Power Sources, 196(8), p3949-3954, (2011). [https://doi.org/10.1016/j.jpowsour.2010.11.093]
• K. Adachi, H. Tajima, T. Hashimoto, and K. Kobayashi, “Development of 16 kWh Power Storage System Applying Li-ion Batteries”, Journal of Power Sources, 119-121, p897-901, (2003).
• A. A. Pesaran, “Battery Thermal Management in EVs and HEVs: Issues and Solutions”, Proceedings of the Advanced Automotive Battery Conference, Las Vegas, (2001).
• G. Karimi, and X. Li, “Thermal Management of Lithium-ion Batteries for Electric Vehicles”, International Journal of Energy Research, 37, p13-24, (2013). [https://doi.org/10.1002/er.1956]
• I. Hadjipaschalis, A. Poullikkas, and V. Efthimiou, “Overview of Current and Future Energy Storage Technologies for Electric Power Applications”, Renewable and Sustainable Energy Reviews, 13(6), p1513-1522, (2009). [https://doi.org/10.1016/j.rser.2008.09.028]
• H. S. Jang, M. G. Park, J. H. Jeon, S. S. Park, T. W. Kim, and S. J. Park, “Experimental Study on Bi-directional Air Cooling System for 18650 Li-ion Battery Module to Minimize Cell-to-Cell Temperature Variation”, Transactions of Korean Hydrogen and New Energy Society, 28(4), p407-418, (2017).
• S. J. Park, and D. H. Jung, “Battery Cell Arrangement and Heat Transfer Fluid Effects on the Parasitic Power Consumption and the Cell Temperature Distribution in a Hybrid Electric Vehicle”, Journal of Power Sources, 227, p191-198, (2013). [https://doi.org/10.1016/j.jpowsour.2012.11.039]
• S. G. Baek, and S. J. Park, “Thermal Analysis of a Battery Cooling System with Aluminum Cooling Plates for Hybrid Electric Vehicles and Electric Vehicles”, Transactions of KSAE, 22(3), p60-67, (2014). [https://doi.org/10.7467/ksae.2014.22.3.060]
• S. K. Mohammadian, and Y. Zhang, “Thermal Management Optimization of an Air-cooled Li-ion Battery Module Using Pin-fin Heat Sinks for Hybrid Electric Vehicles”, Journal of Power Sources, 273, p431-439, (2015). [https://doi.org/10.1016/j.jpowsour.2014.09.110]
• H. Teng, Y. Ma, Y. Kim, and M. Thelliez, “An Analysis of a Lithium-ion Battery System with Indirect Air Cooling and Warm-Up”, SAE International Journal of Passenger Cars - Mechanical Systems, 4(3), p1343-1357, (2011). [https://doi.org/10.4271/2011-01-2249]
• W. M. Kays, M. E. Crawford, and B. Weigand, Convective Heat and Mass Transfer, 4th Edn., McGraw-hill Higher Education, Boston, (2005).
• R. H. S. Winterton, Int. J. Heat Mass Transfer, 2nd Edn., Wiley Hoboken, New Jersey, (1993).
• S. E. Haaland, “Simple and Explicit Formulas for the Friction-Factor in Turbulent Pipe Flow”, Journal of Fluids Engineering, 105, p89-90, (1983). [https://doi.org/10.1115/1.3240948]