GPS와 차량용 센서의 오차와 지연을 고려한 차량용 자세 및 위치 추정 시스템 개발
*This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.
Abstract
In recent years, a high-level driver safety system, such as an autonomous driving system, has been gradually introduced to production vehicles, leading to increasing research on using GPS to control the motion of a vehicle. On the other hand, GPS modules used in production vehicles have a long output period, unlike expensive GPS receivers. Also, precision is relatively low due to the absence of separate devices for correcting errors. To solve these problems, an estimation algorithm was proposed to reduce uncertainty in the location information from GPS, and to obtain a high frequency data rate that would be suitable to control the vehicle. Unlike existing position estimation methods, the proposed algorithm considered both the error in the in-vehicle sensor and the delay in the output signal of the GPS to improve accuracy while still using a simple and effective tracking algorithm. This was verified through a real car experiment with in-vehicle sensor signals and a low-cost GPS receiver.
Keywords:
GPS, Estimation, Latency, In-vehicle sensor, Localization키워드:
전지구위성항법시스템, 추정, 지연, 차량내부센서, 위치추정1. Introduction
자율주행 기술 및 관련된 운전자 보조 시스템에 관한 연구가 진행되면서 점차 차량 내부 센서의 장착 범위가 확대되고 있다. 기존의 차선 이탈 경고와 같은 단일 비전 센서 중심의 어플리케이션에서 시작하여 점차 전방 레이더와 퓨전을 통한 향상된 전방 차로 추종 및 보조 기술이 등장하였다. 뿐만 아니라 위성항법 시스템인 GPS정보를 활용하여 제한속도 적응형 고속도로 자율주행 기술이 이미 양산되는 등 GPS정보를 활용한 연구 범위가 점점 확대되고 있다.21)
GPS는 GNSS 기법 중 하나로 1994년 이후 민간에 공개되면서 다양한 수신기 모듈이 등장하였다. 안테나를 통해 수신한 위성 신호에서 시간을 계측하여 수신기와 위성 사이의 거리를 알아내는 것이 위치의 정확도에 큰 영향을 준다. 따라서 위성 통신에 제약이 있는 구간에서는 위치 정보의 활용이 불가능하다. 한편, 고가의 GPS 수신기는 다양한 밴드의 주파수를 수신할 수 있고, 부가적인 보정신호 처리장치가 장착되어 있어 cm급의 위치 정보를 최소 20 Hz 이상의 주기로 제공 가능하다. 그러나 이러한 수신기는 대체로 고성능의 Active 안테나 뿐만 아니라 보정신호 수신을 위한 모뎀 장비 일체가 포함되기 때문에 승용 차량에 장착하는데 공간적, 비용적 한계가 있다. 반면에 제한된 주파수를 수신할 수 있는 소형의 안테나가 장착된 저가형 GPS 모듈은 차량에 장착할 수 있을 정도로 가격이 저렴하고 소형이지만, 데이터 출력 주기가 1-5 Hz 수준에 상대적인 낮은 위치 정밀도를 가지고 있다.10) 이러한 이유로 처음에는 Navigation과 같이 성능에 영향을 받지 않는 제한적인 용도로 독립적으로 사용이 되던 GPS가 지속적인 연구를 통해 점차 추가적인 정보와의 융합을 통해 저가형 GPS의 성능 한계를 극복하고, 음영지역을 주행하더라도 연속적인 위치 정보를 제공할 수 있게 되었다.
초기의 연구들은 일반 혹은 확장 칼만 필터를 이용하여 차량 내부 Odometer 정보 등을 이용한 필터 기법이 제안되었다.1,7,9) 이후 점차 정밀한 추정 알고리즘8,12,14)이나 상세한 모델이나 복합 모델을 도입하여 성능을 향상시킨 연구11,13)가 진행되어 왔다. 그리고 GPS 정보를 이용해 차량 파라미터를 추정4,5,16) 하거나 차량에 탑재된 오차를 보정하기 위한 연구들이 최근 진행되어 왔다.2,3,6,15,22)
그러나 기존의 연구는 복잡한 모델이나 필터 기법을 사용하여 연산 능력, 시스템의 복잡도가 증가하고 각 모듈 간 의존성이 커 양산 차량에 탑재하기가 현실적으로 어렵다. 한편, GPS에서 출력되는 정보는 이미 내부에 포함된 1차 필터 알고리즘을 거치고, 통신 등을 통해서 정보가 전송되기 때문에 실제 위치나 속도, 방향각과 출력된 정보와는 시간 지연이 존재한다. 기존의 다른 연구18)에서 이를 해결하기 위한 별도의 Buffer에 지연 정보를 모두 저장하는 기법을 제안하였지만, 이로 인하여 저장에 필요한 메모리가 많이 소요되고, 사전 실험을 통해 미리 지연시간을 계측해야 하는 단계가 필요하다.
따라서 본 논문에서는 양산 차량에 탑재가 가능할 수준으로 구조와 연산이 간단하고, 차량 내부 정보만을 이용하여 위치를 추정하는 알고리즘을 제안한다. 뿐만 아니라 각 차량마다 존재하는 센서의 오차와 GPS에 존재하는 지연 요소를 함께 추정함으로써 더 높은 정밀도의 위치와 자세를 지연 없이 제공할 수 있도록 시스템을 구성 하였다. 이어지는 장에서 각 GPS와 차량 내부 센서의 특징을 알아본 후 이어지는 Estimator 설계 파트에서는 방향각이 나타내는 Pose와 Position을 추정하기 위한 필터를 설계한다. 마지막으로 제안된 알고리즘의 성능과 타당성을 검증하기 위하여 실 도로 주행 데이터 기반의 실차 시험을 통한 검증을 수행하였다.
2. GPS 수신 신호의 특징
GPS는 지상의 수신기에 연결된 위성들의 방위각과 거리를 통해 현재 위치를 알아내는 GNSS 시스템 중 하나이다.10) 최초에 GPS는 군사용으로 개발 되었지만 점차 민간에 개방이 되어 실질적인 Navigation이 가능할 정도로 민수용 수신기의 정밀도가 향상되었다. 이러한 GPS 측위의 정확도를 더 높이기 위해 별도의 기준국 보정신호를 수신하여 위치를 보정하는 Differential 방식의 측위 기법도 토목, 해양부문에서 시작하여 점차 확대 적용되고 있다. 이 기준 신호를 수신하는 방법 중 고정 궤도 위성으로부터 정보를 수신하는 Satellite based argumentation system(SBAS) 시스템은 부가적인 수신기의 설치 없이 Standalone GPS 모듈에서 활용 가능한 방식으로 저가형 수신기에서도 활용 가능한 보정 기법이다. 따라서 본 논문에서 사용하는 GPS는 GPS 위성뿐만 아니라 SBAS에 의한 보정 기법이 적용된 신호를 사용한다. 본 논문에서 사용한 자세한 GPS 모듈의 사양은 Table 1과 같다.17)
그리고 GPS에서 계측된 현재의 위치 및 방향각, 속도 등의 정보는 각각 NMEA-0183 포로토콜의 GGA, VTG 메시지에 포함되어 5 Hz의 주기로 출력된다. 각 메시지는 Table 2와 같은 내용을 포함하고 있다.10,17)
이 메시지를 통해서 현재의 위치 뿐만 아니라 진북 방위각(True heading), 속도, 그리고 현재 GPS의 수신 상태를 알 수 있는 신뢰도 정보를 얻을 수 있다. 그러나 GPS의 모든 주파수 대역이 공개되어 있지 않고, 저가형 GPS모듈에서 수신하기 어려운 신호도 존재한다. 또한 위성 궤도는 전리층 바깥에 존재하기 때문에 전파가 전리층을 굴절하며 통과하는 과정에서 전파 도달 시간에 영향을 받는 등의 오차를 항상 수반하게 된다. 뿐만 아니라 동일한 위성이라고 하더라도 항상 궤도를 공전하므로 시간에 따라 전리층을 통과하는 각도가 변하므로 동일한 위치에서도 측위 결과가 변하는 현상이 발생한다.10) 따라서 이러한 위치 오차를 다른 센서의 정보로 Filtering해야 한다.
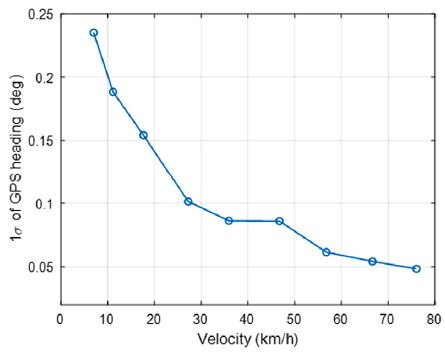
한편 GPS수신기는 위성과의 통신을 통해 추정한 위치를 기반으로 모듈이 장착된 차량의 진행 방향을 계산하여 제공한다. Table 2에서 알 수 있듯이 주어진 상황에서 Heading의 정밀도는 위치의 정밀도에 비해 비교적 높다. 이는 위치 측위 결과에 포함된 오차는 대체로 천천히 변하기 때문에 속도나 방향각을 구하기 위해 위치를 차분 했을 때 오차 성분들이 대부분 Cancel 되기 때문이다. 따라서 이동 속도가 측위 오차가 변하는 속도보다 지배적인 상황에서는 GPS의 속도나 방향각이 정밀하게 측정된다. Fig. 1에서는 이 연구에서 사용하는 실제 GPS 모듈을 차량에 장착하고 5 km/h부터 80 km/h까지 정속 직진 주행을 했을 때 방향각 오차의 표준편차 결과를 보여주고 있다.
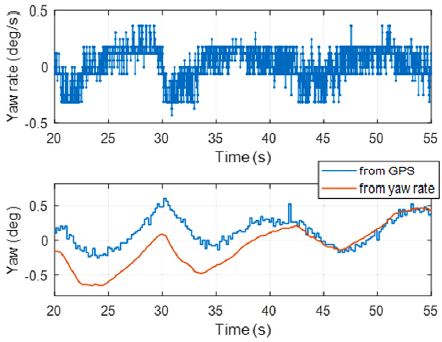
결과에서 저속에서 고속으로 속도가 높아짐에 따라 Heading 표준편차가 점차 지수적으로 감소하여 일반적인 주행상황에서도 0.1도 이내의 표준편차를 가지는 측정 결과를 얻을 수 있다. 다음 Fig. 2는 GPS의 Heading이 얼마나 지연되어 출력되는지 알아보기 위해 GPS에서 출력되는 Heading과 차량 내부 센서인 Yaw rate를 적분하여 비교한 결과를 보여주고 있다.
그림의 상단은 실제 차량에서 계측된 Yaw rate를 보여주고 있다. 그리고 하단의 파란색 선은 GPS에서 출력된 방향각이고, 붉은색 선은 Yaw rate 센서 결과를 수치 적분하여 얻은 방향각을 보여주고 있다. 이를 통해 Peak 지점에서 실제 방향각 보다 GPS의 방향각이 평균적으로 약 300 ms 지연되어 출력되는 것을 확인할 수 있다.
3. In-vehicle 센서의 특성
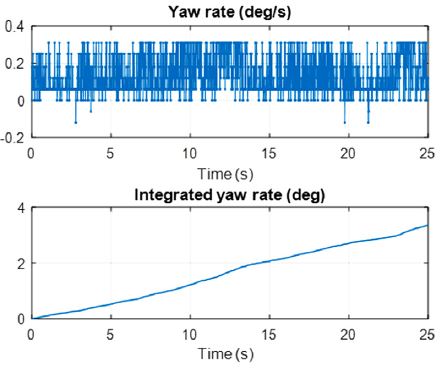
최근 차량의 안전을 위하여 Electric stability control(ESC)의 장착 비율이 지속적으로 증가하고 있으며, 이로 인하여 활용 가능한 차량 내부 정보들이 점차 다양해지고 있다. 따라서 각 휠에 엔코더가 장착되어 각 차륜의 회전 속도를 감지할 수 있고 Yaw rate 센서가 기본으로 장착되어 있다.19) 이 센서들은 차량의 상태를 수시로 감지하고 제어해야 하므로 데이터 출력 주기가 10 ms 이하로, GPS에 비해 빠르다. 따라서 이를 이용해 GPS의 느린 출력 주기를 해결하고 GPS 신호가 수신되지 않는 음영지역에서 Dead reckoning을 수행한다. 먼저 Yaw rate 센서 특성을 파악하기 위하여 다음과 같이 Yaw 운동이 발생하지 않는 정지상태에서 센서 신호를 적분하여 Heading을 생성하는 실험을 Fig. 3에서 보여주고 있다.
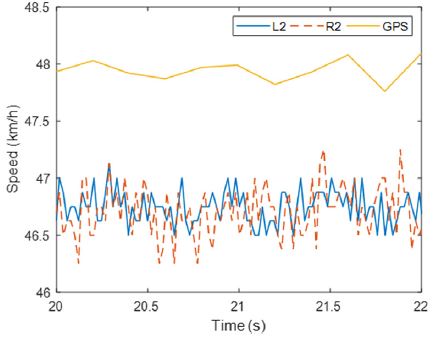
그림의 상단은 실제 차량에 장착된 Yaw rate 센서의 출력값이고, 하단은 이를 이용하여 Heading을 계산한 결과다. 이때 실제로 차량이 회전을 하고 있지 않음에도 불구하고 Yaw rate 센서의 오차에 의해 한쪽 방향으로 점차 발산하고 있는 것을 확인할 수 있다. 이는 차량마다 Yaw rate 센서에서 출력되는 아날로그 전위차의 영점이 미세하기 잘못 설정되어 있기 때문이다. 다음 Fig. 4에는 직선 도로를 등속으로 주행하는 차량의 실험 데이터를 보여주고 있다.
여기서 실선은 후륜 왼쪽의 휠 속도를, 점선은 후륜 오른쪽의 휠 속도를 나타내고, 가장 윗쪽의 실선은 GPS에서 출력된 결과를 나타내고 있다. 이때 정속 주행을 하고 있음에도 불구하고 측정되는 속도에 차이가 발생함을 확인할 수 있다. 실험에서 GPS 속도와 휠의 평균 속도는 약 2 % 정도 오차를 보이고 있다. 이는 차량용 휠 엔코더가 속도가 아닌 각속도를 측정하는데, 실제 타이어의 등가 반지름이 오랜 주행으로 인해 편마모나 공기압의 차이, 혹은 각 휠에 작용하는 수직하중의 차이에 의해 실제와 다를 수 있으므로 GPS 정보와 융합을 할 때 이 점을 고려하였다.
4. 전체 Pose-Position Estimator의 구조
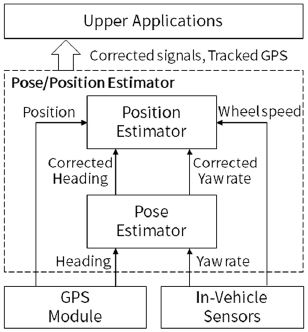
앞서 다룬 GPS와 차량 내부정보의 특성을 고려하여 추정기를 설계하였다. 다음 Fig. 5를 통해 제안하는 추정기의 전체 구조를 보여주고 있다.
그림의 점선으로 표시된 부분이 본 논문에서 제안하는 전체 알고리즘의 범위이다. 하위 레이어인 차량용 센서 모듈 정보와 GPS 모듈 정보를 받아서 상위 알고리즘이 활용할 수 있도록 앞 장에서 살펴본 각 센서들의 문제를 해결하고, 개선된 위치와 Heading을 높은 Date rate로 활용할 수 있도록 추정하는 역할을 수행한다. 제안하는 알고리즘은 크게 2가지 파트로 나뉘어져 있다. 먼저 GPS의 Heading 측정 정보와 차량 내부 센서의 Yaw rate 센서 정보로부터 Heading을 추정하는 Pose estimator가 있다. 더불어 이 블럭에서는 Yaw rate 센서에 포함된 Bias 성분과 GPS heading 정보에 포함된 지연을 함께 추정하여 보정하는 역할도 함께 하고 있다. 두번째 파트는 GPS의 위치 측정 정보와 차량의 휠 속도, 보정된 Heading을 이용해서 현재 차량의 위치 추정을 수행한다. 그리고 각 휠 속도 성분을 GPS 속도 정보를 이용해서 보정하는 역할도 같이 수행한다. 또한 GPS 정보에 포함된 위치정보와 속도 정보의 지연을 함께 State에 포함하여 추정을 한다.
5. Pose Estimator
본 장에서는 진행 방향의 Heading을 추정하는 필터의 설계에 대해서 소개한다. 앞서 실험 데이터를 통해 확인한 바와 같이 Heading 추정을 위해서 Yaw rate 센서 정보를 사용한다. 그러나 센서 자체의 Bias가 존재할 뿐만 아니라 GPS에서 출력되는 Heading 측정값은 표준편차가 0.3도 미만 임에도 약 300 ms 안팎의 지연을 가지고 있다. 이러한 점을 고려하여 확장 칼만 필터(Extended Kalman Filter; EKF) 기법을 활용하여 추정기에 적용 하였다.20) 이때 현재 상태벡터에서 다음 시점의 상태 벡터를 예측하는 Process model은 다음과 같이 정의하였다.
| (1) |
이때 State variable은 xh,k = [ψgps,k ψk γb,k τ-1h,k]T 로, GPS에서 출력된 지연된 Heading, 실제 차량의 Heading, Yaw rate 센서의 Bias, 그리고 지연 시상수의 역수를 의미한다.
여기서 T는 알고리즘의 Sampling time, γyrs는 Yaw rate 센서의 계측 값을 의미한다. Rh,k는 Process model에 대한 노이즈 모델로, yaw rate 센서 성분에 정규분포 형태의 노이즈가 존재한다고 모델링하였다. 그리고 GPS에서 발생하는 지연을 1차 선형 지연으로 가정을 하고 그 시상수를 τh로 모델링하였다. 그러나 위 식의 ψ, ψgps은 각도이기 때문에 2π의 주기를 갖는 Cyclic variable이다. 따라서 이를 고려하여 Process model을 다시 전개하면 다음과 같이 나타낼 수 있다.
| (2) |
여기서 mod(p,q) 함수는 값 p를 q로 Modulo를 취한 결과를 나타내고, ∠(⋅)함수는 입력된 각도의 크기를 [- π,π)범위로 출력하는 역할을 한다. 그리고 확장 칼만 필터에 의해 예측된 다음 상태의 공분산은 다음 식과 같다.20)
| (3) |
예측한 모델을 업데이트 하기 위한 Measurement model은 다음과 같이 GPS에서 출력되는 Heading으로 정의하였다. 여기서 Qh,k는 계측값의 노이즈로, 정규분포를 따른다고 가정을 하였다.
| (4) |
최종적으로 위 Measurement model을 포함한 전체 EKF 업데이트는 다음과 같이 계산한다. 마찬가지로 Cyclic variable을 고려한 Update를 하기 위하여 ∠(⋅)함수를 이용하여 개선된 Update 기법을 제안하였다.
| (5) |
이를 통해 GPS의 Heading의 출력에 지연이 존재한다고 하더라도 이를 개선하고, Yaw rate 센서에 존재하는 Bias와 지연 시상수를 함께 추정이 가능하도록 하였다.
6. Position Estimator
Position estimation 모듈은 앞서 추정한 Heading과 Bias가 제거된 Yaw rate, 그리고 GPS 모듈로부터 현재의 위도, 경도, 속도를 받아서 현재의 위치와 휠속 보정계수를 추정하는 역할을 한다. 먼저 GPS의 위치 및 속도 정보도 앞서 Heading의 경우와 같이 시간 지연이 발생하는 것을 고려하기 위해 각각 1차 지연 모델을 도입 하였다. 그리고 휠 속도의 오차를 표현하기 위해 각각의 휠 속에 곱해지는 보정 계수를 도입 하였다. 상태 변수를 xp,k = [Xk Yk Xgps,k Ygps,k υgps,k τ-1g,kτ-1υ,k αl2,k αr2,k]T로 정의했을 때, x, y는 각각 경도와 위도를, υ는 속도를 나타낸다. τg-1와 τυ-1는 각각 GPS의 위치와 속도 지연을 나타내는 시상수의 역수이고, α는 해당 차륜의 Scale factor를 나타낸다. 만약 휠 속도가 실제 속도와 동일하다면 α = 1을 만족한다. 경도와 위도를 각각 (x, y)와 (xgps, ygps)로 구분한 것은 실제 현재 위치와 GPS 모듈에서 출력되는 지연된 위치를 모델링 하기 위해서이다. 위와 같이 정의한 상태변수를 이용하여 Process model을 표현하면 다음 식과 같다.
| (6) |
여기서 Rp,k는 Process model로 다음 상태를 예측할 때 발생하는 노이즈를 나타내며, 본 논문에서는 정규분포를 따른다고 가정 하였다. 마찬가지로 예측 단계에서 Covariance matrix는 다음과 같이 전이된다.
| (7) |
여기서 Gp는 Process model의 Jacobian matrix이다. 그리고 예측한 위치와 속도 등을 보정하기 위한 계측 값으로, GPS에서 출력되는 경도, 위도, 속도, 그리고 앞서 Bias가 제거된 Yaw rate 센서 정보를 사용한다. 이를 Measurement model로 표현을 하면 다음 수식과 같다.
| (8) |
여기서 γ*yrs는 앞서 추정된 Yaw rate로, γyrs + γb와 같다. 그리고 t는 양쪽 타이어 사이의 간격으로, 양쪽 휠 속도의 차이는 Yaw rate와 휠 간격을 곱한 값과 동일하기 때문에 위 수식과 같이 나타낼 수 있다. 여기서 Qp는 Measurement noise를 나타내며 각각의 원소들은 정규분포 노이즈를 따른다. 이때, Extended kalman filter를 적용하면 다음 수식과 같이 관측값을 이용하여 예측한 State를 업데이트 할 수 있다.
| (9) |
여기서 Kp는 Position estimator를 위한 Kalman gain을 의미한다. 최종적으로 앞 장의 Pose estimator와 본 Position estimator를 통해 GPS 음영지역에서도 연속적으로 위치 정보를 활용할 수 있을 뿐만 아니라 높은 Date rate로 상위 응용 레이어에 정보를 제공할 수 있다. 그리고 차량 내부 센서인 Yaw rate와 후륜 양 휠 속도의 오차를 보정하여 더 정확하게 위치 및 자세를 얻을 수 있다.
7. Experiment Results
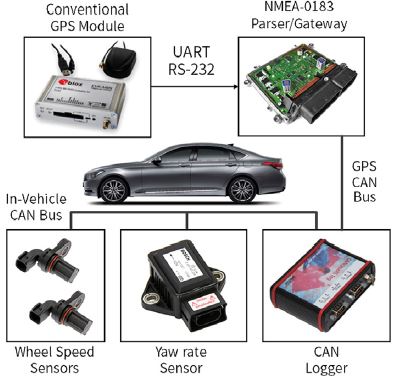
제안된 알고리즘을 검증하기 위해서 실험을 수행하였다. 실제로 양산되는 차량에 저가형 GPS를 탑재하여 일반 도로를 주행하여 얻은 데이터를 기반으로 검증을 수행 하였다. Fig. 6에서 데이터 취득을 위한 실험 구성을 보여주고 있다.
차량에서 사용하는 CAN 통신 내용을 기록하기 위한 CAN Logger가 설치되어 있고, 각 채널 별로 휠 속도와 Yaw rate 정보가 포함된 In-vehicle CAN 버스와 GPS 정보가 출력되는 GPS CAN을 동기화해서 Logging을 수행한다. 여기서 GPS 모듈은 시리얼 통신(UART)를 통해 출력되기 때문에 프로토콜을 해석하고 CAN으로 변환하는 게이트웨이가 함께 장착되었다. 이때 GPS 수신기는 후륜의 차축 중앙에 해당하는 위치의 천장에 설치 되었다. 이때 차량의 센서 정보는 10 ms마다, 그리고 GPS 정보는 200 ms마다 출력되는 환경에서 검증을 진행하였다.
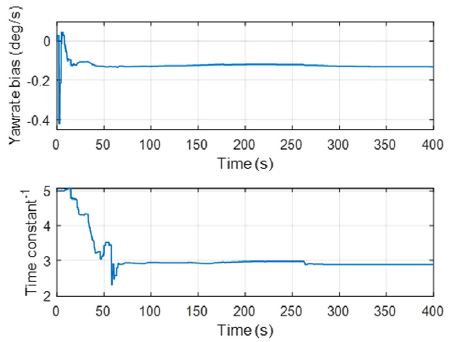
다음 Fig. 7은 주행 중 실시간으로 Pose estimation 모듈에서 Heading bias와 시상수의 역수를 추정하는 결과를 각각 상단과 하단의 그래프에 나눠서 보여주고 있다.
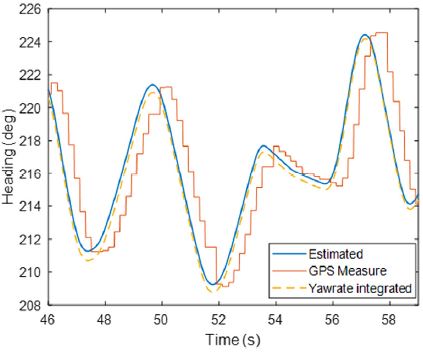
그림에서 확인할 수 있듯이 시간에 따라서 점차 Yaw rate bias의 경우 약 -0.13 deg/s, Heading 출력 지연의 시상수의 경우 약 360 ms 수준으로 추정됨을 확인할 수 있다. GPS 신호 지연의 보상 결과는 다음 Fig. 8에서도 확인 가능하다.
그림의 파란색 실선은 제안된 추정기에 의해 추정된 Heading이고, 빨간색의 계단형 실선은 GPS에서, 그리고 노란색 점선은 위상 지연 여부를 확인하기 위하여 차량의 Yaw rate 센서를 적분하여 얻은 Heading이다. 그림과 같이 GPS에서 낮은 Rate로 나오는 출력을 차량 내부정보를 통해 10 ms마다 Tracking을 하고 있을 뿐만 아니라 GPS의 지연된 Heading 출력을 보완하고 있음을 확인할 수 있다. 다음은 Position estimation 모듈을 실험을 통해 검증한 결과이다. 먼저 해당 추정기에서 후륜 휠 속도 계수와 각 정보의 지연을 추정한 결과를 다음 Fig. 9를 통해 확인할 수 있다.
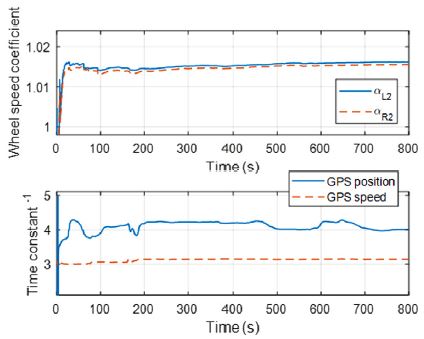
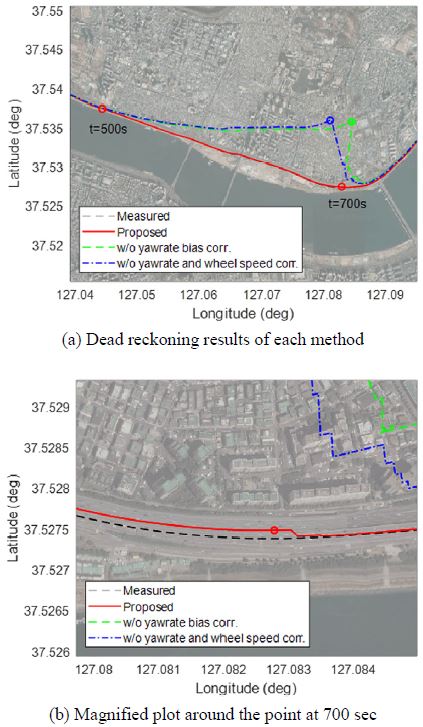
먼저 그림의 상단은 휠 속도의 계수이다. 각 타이어의 마모도 및 수직 하중 등의 영향을 받아 경미하게 다르지만 양측 모두 대체로 약 1.7 %의 오차를 보이고 있다. 그리고 하단의 그림은 각 신호 별 시상수의 역수를 추정한 결과를 보여주고 있다. 여기서 실선과 점선은 GPS 위치정보와 GPS 속도정보의 시상수로 각각 250 ms, 300 ms로 추정됨을 확인할 수 있다. 다음 Fig. 10은 제안된 알고리즘의 성능을 검증하기 위하여 추정된 위치를 위성 사진과 겹친 결과를 보여주고 있다. 그림의 자동차 도로를 좌측에서 우측으로 동쪽을 향해서 주행을 하였다.
차량 내부정보를 보정하는 알고리즘의 영향을 확인하기 위하여 오직 Yaw rate 센서만 보정한 결과를 녹색 파선으로, Yaw rate 센서 및 휠 속 어떤 것도 보정하지 않은 결과를 파란색 점선으로, 그리고 제안된 기법의 결과는 빨간색 실선으로 그려져 있다. 그리고 참고를 위해 정상적인 상황에서 계측한 실제 위치는 검정색 파선으로 그려져 있다. 실험 중 의도적으로 500에서 700초 구간인 200초 동안 GPS에서 입력되는 정보를 차단하고 Dead reckoning만 수행하였고, 700초부터 다시 GPS 정보가 수신되도록 하였다. 여기서 GPS 수신이 끊어지기 시작한 500초의 위치가 상단 그림 왼쪽의 ‘o’ 형태의 마커로 표현되어 있고, 각각 Dead reckoning을 수행하다가 GPS가 다시 계측되기 시작하기 직전인 700초의 위치를 각선의 색상인 ‘o’ 형태의 마커로 표시를 하였다. 먼저 아무것도 보정하지 않고 Dead reckoning을 한 결과인 파란색 선 결과와 오직 휠 센서만 보정을 한 초록색 선 결과를 살펴보면, 두 결과 모두 편향된 Yaw rate 센서 정보로 인하여 점차 실제 주행한 위치에서 잘못된 방향으로 위치가 추정되고 있음을 확인할 수 있다. 그리고 휠 속도 보정을 하지 않은 파란색 파선의 결과는 휠 속도 보정이 되지 않아 종방향으로 실제 주행 거리보다 짧게 추정이 되고 있다가 GPS가 업데이트 되면서 점차 원래 위치로 수렴해가고 있다. 이에 반해 제안된 알고리즘의 결과인 빨간색 실선은 200초 동안 Dead reckoning을 수행하더라도 실제 주행한 검정색 파선과 겹쳐져 큰 차이를 보이지 않고 있다. 이를 비교하기 위하여 하단의 그림에서 Update가 일어나는 700초 구간을 확대하여 보여주고 있다. 여기서 제안된 알고리즘은 200초의 Dead reckoning 이후 Update될 때 횡방향으로 약 10.8 m, 종방향으로 약 8 m의 오차를 보여 기존의 차량 내부정보를 보정하지 않는 기법 대비 높은 정확도를 보여주고 있다.
8. Conclusions
- 1) 본 논문에서는 저가형 GPS와 차량 내부정보만 을 활용한 위치 추정 알고리즘을 제안
- 2) 차량 내부 센서에 포함된 오차들을 제거하고, 저가형 GPS모듈에서 발생한 시간 지연을 반영하여 향상된 위치 추정 및 Dead reckoning 성능을 확보
- 3) 제안된 알고리즘은 Pose와 Position을 각각 나누어 추정하는 Cascade 구조로 구성함으로써 전체적인 시스템의 복잡도를 분산하고, 사용되는 모델 행렬의 크기를 줄여 연산 부담을 줄임
- 4) GPS를 실 차량에 탑재하여 취득한 데이터를 기반으로 검증을 수행 하였고, 제안된 기법과 제안된 기법이 포함되어 있지 않은 기존 알고리즘과 비교를 하여 개선된 성능을 검증함
Nomenclature
| G : | jacobian matrix of process model |
| H : | jacobian matrix of measurement model |
| P : | covariance matrix |
| Q : | noise of measurement model |
| R : | noise of process model |
| T : | sampling time, sec |
| K : | kalman gain |
| X : | longitude, deg |
| Y : | latitude, deg |
| g : | process model |
| h : | measurement model |
| v : | velocity, m/s |
| x : | state variable vector |
| z : | measurement state variable |
| α : | coefficient of velocity error |
| γ : | yaw rate, rad/s |
| τ : | time constant, sec |
| ψ : | yaw, heading, rad |
Subscripts
| b : | bias |
| gps : | information from the GPS module |
| h : | heading/pose related states/matrices |
| k : | current time step |
| l2, r2 : | left or right side of rear axle |
| p : | position related states/matrices |
| yrs : | information from yaw rate sensor |
Acknowledgments
본 연구는 국토교통부/국토교통과학기술진흥원의 지원으로 수행되었음(과제번호: 18TLRP-B101406-04).
References
-
E. Abbott, and D. Powell, “Land-vehicle Navigation Using GPS”, Proceedings of the IEEE, 87(1), p145-162, (1999).
[https://doi.org/10.1109/5.736347]

-
M. F. Abdel-Hafez, “On the GPS/IMU Sensors' Noise Estimation for Enhanced Navigation Integrity”, Mathematics and Computers in Simulation, 86, p101-117, (2012).
[https://doi.org/10.1016/j.matcom.2010.03.005]

- M. F. Abdel-Hafez, K. Saadeddin, and M. Amin Jarrah, “Constrained Low-cost GPS/INS Filter with Encoder bias Estimation for Ground Vehicles Applications”, Mechanical Systems and Signal Processing, 58, p285-297, (2015).
-
K. Berntorp, “Joint Wheel-Slip and Vehicle-Motion Estimation Based on Inertial, GPS, and Wheel-Speed Sensors”, IEEE Transactions on Control System Technology, 24(3), p1020-1027, (2016).
[https://doi.org/10.1109/tcst.2015.2470636]

-
D. M. Bevly, “Global Positioning System (GPS): A Low-Cost Velocity Sensor for Correcting Inertial Sensor Errors on Ground Vehicles”, Journal of Dynamic Systems, Measurement, and Control, 126, p255, (2004).
[https://doi.org/10.1115/1.1766027]

-
D. M. Bevly, and B. Parkinson, “Cascaded Kalman Filters for Accurate Estimation of Multiple Biases, Dead-reckoning Navigation, and Full State Feedback Control of Ground Vehicles”, IEEE Transactions on Control Systems Technology, 15, p199-208, (2007).
[https://doi.org/10.1109/tcst.2006.883311]

-
P. Bonnifait, P. Bouron, P. Crubillc, and D. Meizel, “Data Fusion of Four ABS Sensors and GPS for an Enhanced Localization of Car-like Vehicles”, Proceedings 2001 ICRA, p1597-1602, (2001).
[https://doi.org/10.1109/robot.2001.932839]

-
L. Chang, K. Li, and B. Hu, “Huber's M-estimation-based Process Uncertainty Robust Filter for Integrated INS/GPS”, IEEE Sensors Journal, 15(6), p3367-3374, (2015).
[https://doi.org/10.1109/jsen.2014.2384492]

- J. Gao, M. G. Petovello, and M. E. Cannon, “Development of Precise GPS/INS/Wheel Speed Sensor/Yaw Rate Sensor Integrated Vehicular Positioning System”, Proceedings of the 2006 National Technical Meeting of the Institute of Navigation, p780-792, (2006).
- B. Hofmann-Wellenhof, H. Lichtenegger, and E. Wasle, GNSS - Global Navigation Satellite Systems - GPS, GLONASS, Galileo, and More, Springer Science, New York, (2008).
-
K. Jo, K. Chu, and M. Sunwoo, “Interacting Multiple Model Filter-Based Sensor Fusion of GPS With In-Vehicle Sensors for Real-Time Vehicle Positioning”, IEEE Transactions on Intelligent Transportation Systems, 13(1), p329-343, (2012).
[https://doi.org/10.1109/tits.2011.2171033]

-
T. A. Johansen, T. I. Fossen, and G. C. Goodwin, “Three-stage Filter for Position Estimation Using Pseudorange Measurements”, IEEE Transactions on Aerospace and Electronic Systems, 52, p1631-1643, (2016).
[https://doi.org/10.1109/taes.2016.150362]

-
K. T. Leung, J. F. Whidborne, D. Purdy, and P. Barber, “Road Vehicle State Estimation Using Low-cost GPS/INS”, Mechanical Systems and Signal Processing, 25, p1988-2004, (2011).
[https://doi.org/10.1016/j.ymssp.2010.08.003]

-
Y. Liu, X. Fan, C. Lv, J. Wu, L. Li, and D. Ding, “An Innovative Information Fusion Method with Adaptive Kalman Filter for Integrated INS/GPS Navigation of Autonomous Vehicles”, Mechanical Systems and Signal Processing, 100, p605-616, (2018).
[https://doi.org/10.1016/j.ymssp.2017.07.051]

-
J. Ryan, and D. Bevly, “Tire Radius Determination and Pressure Loss Detection Using GPS and Vehicle Stability Control Sensors”, IFAC Proceedings, 45(20), p1203-1208, (2012).
[https://doi.org/10.3182/20120829-3-mx-2028.00090]

- J. Ryu, E. J. Rossetter, and J. C. Gerdes, “Vehicle Sideslip and Roll Parameter Estimation using GPS”, Proceedings of the AVEC, p373-380, (2002).
- U-blox, NEO-M8 Concurrent GNSS Modules, U-blox Data Sheet (2015).
-
S. Weiss, M. W. Achtelik, M. Chli, and R. Siegwart, “Versatile Distributed Pose Estimation and Sensor Self-calibration for an Autonomous MAV”, IEEE International Conference on Robotics and Automation, p31-38, (2012).
[https://doi.org/10.1109/icra.2012.6225002]

- K. Rief, and K. H. Dietsche, Bosch Automotive Handbook, 9th Edn., Wiley, New Jersey, (2011).
-
C. K. Chui, and G. Chen, Kalman Filtering with Real-Time Applications, Springer International Publishing, New York, (2017).
[https://doi.org/10.1007/978-3-662-02508-6]

-
K. Lee, J. Bak, and C. Lee, “A Study on DGPS/GIS-based Vehicle Control for Safe Driving”, “A Study on DGPS/GIS-based Vehicle Control for Safe Driving,”, 21(5), p54-58, (2013).
[https://doi.org/10.7467/ksae.2013.21.5.054]

-
J. Yee, T. Kim, and H. Kim, “Vehicle Position Estimation Using Low-cost RTK Module, Wheelpulse, and IMU Sensor”, Transactions of KSAE, 26(3), p407-415, (2018).
[https://doi.org/10.7467/ksae.2018.26.3.407]