[ Article ]

Transactions of The Korean Society of Automotive Engineers - Vol. 26, No. 2, pp.174-186

ISSN: 1225-6382 (Print) 2234-0149 (Online)

Print publication date 01 Mar 2018

Received 30 Nov 2017 Revised 13 Dec 2017 Accepted 21 Dec 2017

DOI: https://doi.org/10.7467/KSAE.2018.26.2.174

정상유동 장치에서 유동 특성 평가 방법에 대한 연구(6) : 축 방향 속도의 영향

양철호¹⁾

; 엄인용^*^{, 2)}

1)서울과학기술대학교 에너지환경전문대학원
2)서울과학기술대학교 기계･자동차공학과

Study on Evaluation Method of Flow Characteristics in Steady Flow Bench(6) : Effect of Axial Velocity

Cheolho Yang¹⁾

; Inyong Ohm^*^{, 2)}

1)Graduate school of Energy & Environment, Seoul National University of Science and Technology, Seoul 01811, Korea
2)Department of Mechanical & Automotive Engineering, Seoul National University of Science and Technology, Seoul 01811, Korea

Correspondence to: ^*E-mail: iyohm@seoultech.ac.kr

* This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.

Abstract

In the previous studies, the assumption of the solid rotation, the velocity profiles, the evaluation position, and the eccentricities were discussed. In addition, the swirl coefficient and swirl ratio were assessed and compared via measurement of the conventional impulse swirl meter(ISM) and calculation based on the velocity by particle image velocimetry(PIV) from 1.75B position, which was 1.75 times bore position apart from the cylinder head, to the 6.00B position. In this study, the influence of the axial flow on the flow evaluation was examined from 1.75B position to the 6.00B position in order to check the constant axial velocity assumption. For this purpose, the evaluation was performed under the assumption that the axial velocity is proportional to the tangential velocity, and the results were compared with the previous ones. The results showed that the influence of the axial velocity was larger than the effect of the evaluation center setting. Also, the swirl coefficient increased because the increase in momentum around the cylinder wall was much larger than the decrease of the one around the evaluation center when the axial velocity was considered. Furthermore, the tangential and axial velocity distributions were quite similar, but there was also a backflow by recirculation in the axial direction, thereby distorting the measured values. On the other hand, when the momentum was conserved, the swirl coefficient measured by the ISM changed according to the measurement plane position due to the momentum conversion caused by the flow structure change. In the ISM evaluation before 5B, the effects of the change of the flow structure and the backflow were significant. After 5B, the effect of friction increased because the structural change was reduced by the flow development. Finally, despite the angle of attack variation due to the flow progression, its effect was not observed because the influences of tangential and axial flows were offset against each other, and the evaluation value increased as the structure of the flow gradually turned to the ideal form in the evaluation of the PIV.

Keywords:

Steady flow bench, Swirl, ISM, PIV, Velocity profile, Axial velocity, Intake valve angle, Momentum, Eccentricity

키워드:

정상유동장치, 스월, 충격식 스월 측정기, 입자영상유속계, 속도분포, 축 방향 속도, 흡기밸브각도, 운동량, 편심

1. 서 론

지금까지 내연기관 내부유동 평가에서 발생하는 여러 문제점에 밸브각도(V/A, valve angle)를 변경하면서, 대표적인 정상유동 평가방법인 충격식 스월 측정기(ISM, impulse swirl meter)와 입자영상유속계(PIV, particle image velocimetry) 결과를 비교하였다. 이전 연구 결과를 용약하여 제시하면 다음과 같다.

현행 방법에서 스월의 강체 회전 가정이 가장 큰 오차를 발생시키고, 스월 중심이 편심되어 있으면 편심도는 실제 토크에 큰 영향을 주지만 충격식 스월 측정기로는 편심의 효과를 확인할 수 없으며, 스월 속도분포뿐만 아니라 축 방향 속도분포도 실제 토크에 큰 영향을 준다.¹⁾ 또한 현재 측정 방법을 사용하면 스월의 편심과 속도 분포는 모두 유동 특성을 왜곡시키지만 편심은 과소평가 쪽으로 그리고속도분포는 과대평가 쪽으로 작용하고, 속도분포의 영향이 편심보다 훨씬 크고 지배적이다.²⁾ 아울러 현재 통상적으로 사용하는 측정 위치에서 실제 속도분포 특성은 충격식 스월 측정기 평가의 가정과 매우 다르다는 것을 관찰하였다.³⁾

측정 위치가 하류로 가면 속도 분포는 개선되지만 편심은 여전히 크게 존재한다.⁴⁾ 마지막으로 SM 평가에서, 측정위치가 하류로 갈수록 꾸준히 스월계수는 감소하고 리프트 변화에 따른 변화의 형태가 단순해지며 직선적 증가의 경향이 두드러지고, 반면 PIV 기반 평가에서는 측정위치가 하류로 갈수록 스월계수는 증가하고 증가폭은 리프트가 높을수록 크다.⁵⁾ 이를 통하여 축 방향 속도 분포의 영향과 운동량 변환에 대한 검토가 필요하다는 결론에 도달하였다.

본 연구에서는 축 방향 속도를 고려한 평가 결과를 제시하고, 이를 실린더 중심 평가와 비교하며 운동량 변환에 대해 논의하기로 한다.

2. 실험 장치 및 방법

Fig. 1에 본 연구에서 사용된 흡기밸브각도가 서로 다른 4개 헤드의 개략도를 제시하였는데, 유동평가 시 2개 흡기밸브 중 후측(Rear) 밸브만 개방하여 스월 유동이 형성되도록 하였다.

Fig. 1

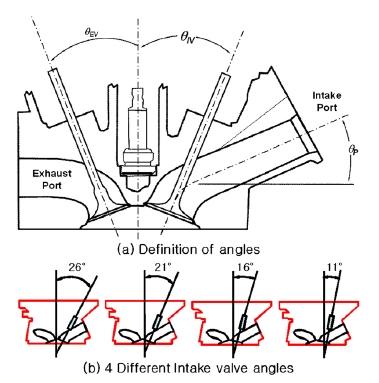
(a) Definition of angles (θIV : intake valve angle, θEV : exhaust valve angle and θP : intake port angle) and (b) Schematics of 4 head with different intake valve angle

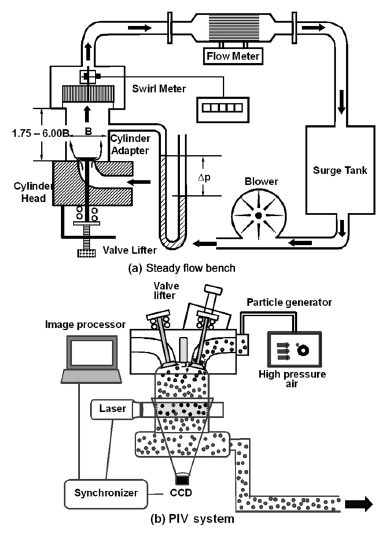
Fig. 2는 실험장치의 개략도이며, ISM(G. Cusson사 P7300/200)은 통상적인 ISM 측정위치인 1.75B(실린더 하면에서 보어의 1.75배 하류)를 포함하여 3.00, 4.50, 6.00B에 장착하였고, 동일 위치에서 PIV 측정도 병행하였다. 실험 조건과 기타 PIV 시스템의 사양은 Table 1에 나타내었으며, ISM의 경우 밸브 리프트를 1 ~ 10 mm까지 1 mm 간격으로 변화시켰고, PIV에서는 밸브 리프트 2, 3, 6, 8, 10 mm에서 실시하였다. 자세한 장치의 설명과 실험방법은 이전 논문^1-5)에서 다루었기 때문에 생략한다.

Fig. 2

Schematics of (a) Steady flow bench and (b) PIV system

Table 1

Experimental conditions and specifications of PIV

PIV로 측정한 속도로 토크(Moment of momentum flux)와 반경 방향의 각종 운동량을 구하는 방법은 다음과 같다.^6,7)

T = ∫ 0 B / 2 ∫ 0 2 π ρ υ z r, θ υ θ r, θ r 2 d r d θ

(1)

한편 본 연구에서는 축 방향 속도를 측정하지 않았으므로 이전 연구^3,4)에서 언급한 바와 같이 축 방향 속도가 평면 속도에 비례한다고 가정하면

υ z, i = υ z ∙ υ i / υ ¯

식 (1)의 좌표계를 PIV 측정에서 사용한 직교 좌표계로 변환하고 구분구적법을 적용하면

T = ∑ i ρ i υ z, i r i υ θ, i ∆ x ∆ y

(2)

= ∑ i ρ i υ z, i r i υ y, i cos ⁡ θ - υ x, i sin ⁡ θ ∆ x ∆ y

여기서 $υ ¯$ 는 평균 평면속도이고 $υ z$ 는 체적 유량을 실린더 단면적으로 나눈 값을 사용하였다.

전체 평면에 걸쳐 밀도(ρ)가 동일하면

T = ρ ∑ i r i υ z, i υ y, i C O S θ - υ x, i s i n θ ∆ x ∆ y

(3)

측정 속도를 기반으로 토크를 계산할 때, 요소면적(Element area)까지의 거리 r_i의 설정 및 축 방향속도의 고려 방법에 따른 차이를 Table 2에 제시하였다. 제시된 네 가지 방법 중 원리적으로는 실린더 중심을 기준으로 축 방향 속도를 고려한 C_CA가 ISM 측정에 상응한다.

Table 2

Momentum according to evaluation method

스월계수(N_r)와 스월비(R_s)는 다음과 같이 구하였다.^6,7)

N r = ω c ∙ B ∙ m ̇ υ 0 ∙ m ̇ = 8 T m ̇ υ 0 B

(4)

R s = ω c ω e = B S π n D 2 ∫ α 1 α 2 C f N r d α ∫ α 1 α 2 C f d α 2

(5)

3. 결과 및 검토

Fig. 3에 V/A 11°일 때, PIV 측정을 기반으로 Table 2에 제시한 네 개의 방법을 적용하여 스월 계수를 평가한 결과를 측정위치 별로 제시하였다. ISM과 PIV 평가와의 차이 및 평가 위치에 따른 변화는 이전 연구⁵⁾에서 논의하였고 서론에 제시하였으므로 간략히 하고, 축 방향 속도의 영향에 주목하여 논의하면 다음과 같다.

Fig. 3

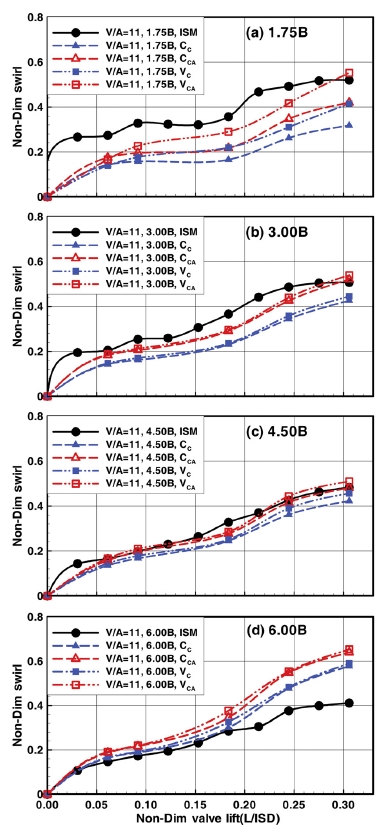
Non-dimensional rig swirl as a function of non-dimensional valve lift according to evaluation position when V/A=11°

측정위치 1.75B에서 PIV 평가는 ISM 보다 낮지만 예외적으로 리프트 10 mm(무차원 리프트 0.3058)에서 V_CA 평가가 ISM 보다 높다. PIV 평가 내에서는 중심 설정에 관계없이 축 방향 속도를 고려한 경우가 높으며 동시에 스월 중심의 평가가 높다. 그리고 ISM에 상응하는 C_CA는 ISM의 50 ~ 80 % 수준이다.

3.00B에서는 중심 설정에 따른 차이가 거의 나타나지 않고, 축 방향 속도에 따른 차이만 뚜렷이 나타나서 C_CA와 V_CA가 거의 같고 C_C와 V_C도 대체로 일치한다. ISM과 C_CA는 1.75B보다 상대적 차이가 줄어들어 ISM의 80 % 이상이고, 1.75B에서와 같이 리프트 10 mm에서는 ISM보다 조금 높다.

4.50B에서는 3.00B에서 줄어들었던 중심 설정에 따른 차이가 다시 소폭 커지지만, 축 방향 속도에 따른 차이는 줄어든다. 아울러 축 방향 속도를 고려한 경우 ISM의 평가와 거의 일치하며, V_CA 평가에서는 리프트 8 mm(무차원 리프트 0.2752) 이상에서 ISM 평가보다 높다.

마지막으로 6.00B에 도달하면 PIV 평가 값이 대폭 증가하면서 모든 평가 값이 ISM 보다 높다. 그리고 4.50B에서 줄어들었던 축 방향 속도에 의한 차이가 다시 증가하고, 중심 설정에 따른 차이는 거의 나타나지 않는다.

이러한 PIV 평가방법 및 위치에 따른 변화를 Fig. 4에 나타낸 운동량 유속(Momentum flux) 분포의 변화를 참조하며 논의하기로 한다. 여기서 리프트에 따라 정량적 변화만 있고 정성적으로는 동일하며, 리프트 10 mm에서 이러한 변화가 가장 극명하게 나타나므로 10 mm에 대해서만 제시하였다.

Fig. 4

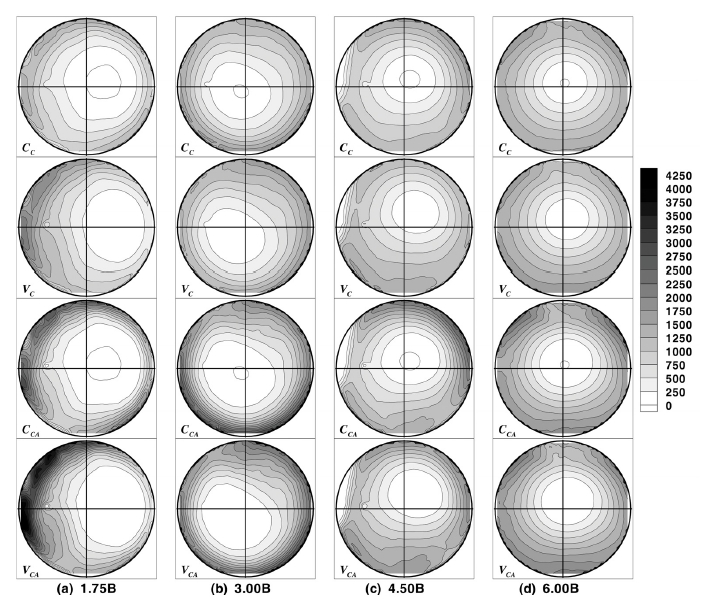
Momentum flux distribution of V/A 11° port according to evaluation position and method at 10 mm valve lift

평가위치에 따른 운동량 분포는 하류로 갈수록 평가 방법에 무관하게 이상적 분포 즉 실린더 중심을 기준으로 한 동심원 형태의 분포에 가까워진다. 이는 이전연구에서 살펴보았듯이 하류로 갈수록 속도 분포가 이상적 형태로 변하기 때문에 나타나는 자명한 결과이다.⁴⁾

먼저 1.75B에서 운동량은 일정 영역에만 집중되어 있는데, 이러한 경향은 축 방향 속도를 고려하는 경우 및 스월 중심으로 평가할 때 더 뚜렷이 나타난다. 중심 설정에 의한 차이가 가장 두드러지는 것은, 이전 연구³⁾에서도 지적했듯이 이 위치에서 편심이 크기 때문에 스월 중심의 경우 속도 분포가 한쪽으로 치우쳐져 있어 운동량 분포도 달라지기 때문이다. 즉 스월 중심과 가까운 실린더 벽 주변의 운동량은 실린더 중심의 경우보다 감소하지만, 스월 중심과 먼 실린더 벽 주변의 운동량은 증가한다. 그리고 운동량이 증가한 영역의 면적이 감소한 영역보다 훨씬 크기 때문에 편심에 의해 전체적으로 스월 계수가 증가한다.

3.00B에서는 축 방향 속도를 고려한 경우에만 운동량 집중에 차이가 나기 때문에, 중심 설정에 의한 차이는 줄어들고 축 방향 속도의 영향이 크게 나타난다. 다른 평가 위치에서도 절대량의 차이는 있지만 이와 동일한 기구 즉 편심에 의한 운동량 분포 차이가 중심 설정에 따른 차이의 원인이다. 구체적으로 4.50B에서 중심 설정에 의한 차이가 소폭이지만 다시 증가하는 것도 역시 이 위치에서의 편심이 3.00B와 6.00B보다 큰 것이 원인이다.

동일 위치에서 평가방법에 따른 변화를 보면, 축 방향 속도를 고려하면 평가 중심에 가까운 운동량이 작은 영역의 면적이 확대된다. 이것은 이 영역의 축 방향 속도가 평균 속도보다 낮기 때문이다. 이후 중심 부근의 낮은 운동량 영역을 벗어나면, 축 방향 속도는 평균 속도 보다 높고 바깥쪽으로 갈수록 크기 때문에 운동량 구배가 증가하여 등고선 간격이 좁아진다. 이 때 중심 주변의 운동량 감소보다 실린더 벽 주변의 증가가 훨씬 크기 때문에 축 방향 속도를 고려하면 스월 계수가 증가한다.

추가로 축 방향 속도를 고려할 때, 중심 설정에 따라 운동량이 집중되는 영역이 달리 나타나는데, 이는 편심에 의해 중심에서의 거리가 달라지기 때문이지만 전체 스월 계수에 미치는 영향은 적다.

Fig. 5에는 V/A 16°의 스월 계수를 도시하였는데, 이를 11°와 비교하면, 리프트 변화에 따른 스월 계수의 세밀한 변화에는 차이가 있지만, 전체적인 변화의 경향은 11°와 매우 유사하다. 즉 1.75B에서는 PIV 평가가 ISM 보다 항상 낮고 중심 설정과 축 방향 속도에 따라 평가 값에 차이가 난다. 그러나 3.00B에서는 축 방향 속도에 의한 차이는 존재하지만 중심 설정에 따른 차이는 거의 없다. 4.50B에서 축 방향 속도에 의한 차이가 소폭 증가하지만 6.00B에서 다시 차이가 감소한다.

Fig. 5

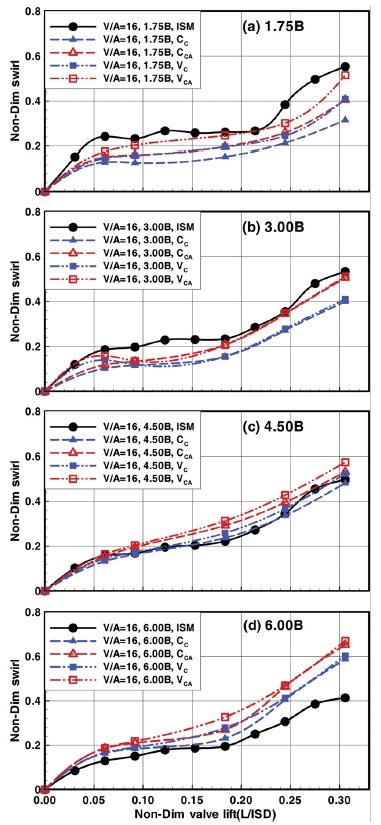
Non-dimensional rig swirl as a function of non-dimensional valve lift according to evaluation position when V/A=16°

11°와 차이가 나는 부분은 평가위치에 따른 ISM과 PIV의 상대적인 크기인데, 11°는 4.50B에서 ISM과 PIV 평가가 근접하고 6.00B에서 PIV가 높아지는데 반해, 16°에서는 PIV 평가가 높아지는 위치가 4.50B로 약간 상류로 이동한다.

이러한 V/A 16°에서의 변화는 11°에서의 변화와 동일한 기구에 의한 것이고, 실제 운동량 분포의 경향도 11°와 매우 유사하므로 제시하지 않고, 관련된 논의도 11°의 경우로 갈음한다.

Fig. 6에는 V/A 21°의 경우를 도시하였다. 이를 앞에서 논의한 V/A 11° 및 16°와 비교하면, 평가위치와 방법에 따른 전체적인 변화의 경향은 일치하지만 몇 가지 미세한 차이점을 발견할 수 있다.

Fig. 6

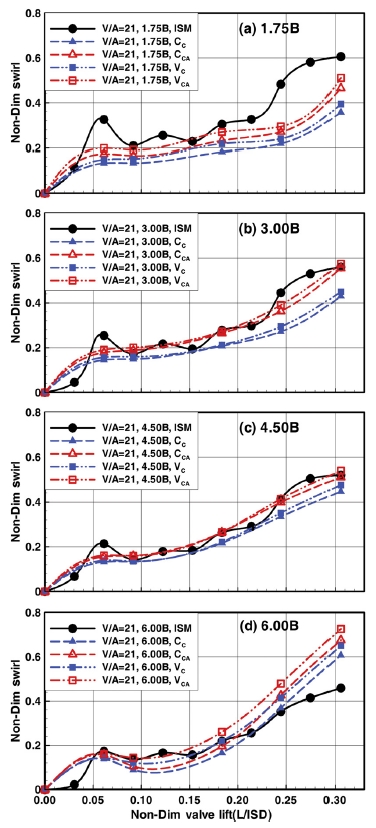
Non-dimensional rig swirl as a function of non-dimensional valve lift according to evaluation position when V/A=21°

먼저 V/A 11° 및 16°에서는 1.75B 이후의 평가위치에서 중심 설정에 의한 차이가 없는 경우가 있지만, 21°에서는 모든 위치에서 중심 설정에 의한 차이가 작지만 비교적 분명히 나타난다. 또한 1.75B에서 축 방향 속도 가정에 따른 차이는 이전에 비해 줄어들고, 리프트 10 mm에서 V_CA에 의한 평가가 ISM보다 상당히 낮다. 마지막으로 1.75B에서 ISM과 PIV와의 차이가 상당히 크지만, 3.00B와 4.50B에서는 리프트에 따라 다소 변동이 있지만 대체로 일치한다.

여기서 평가위치 및 방법에 따라 스월 계수의 변화에서 여러 구체적인 차이가 관찰되지만, 이전의 경우와 같이 평가위치 및 방법의 변화가 운동량 분포의 변화에 미치는 기구는 Fig. 7에서 관찰할 수 있는 바와 같이 본질적으로 동일하기 때문에 제시만 하고 논의는 생략한다.

Fig. 7

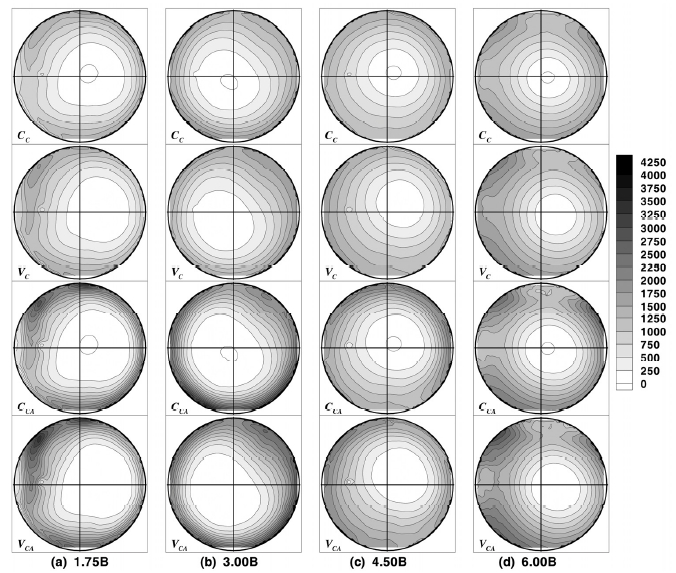
Momentum flux distribution of V/A 21° port according to evaluation position and method at 10 mm valve lift

Fig. 8에는 V/A 26°의 경우를 도시하였는데, 이 경우 이전 연구에서와 같이^3-5) 다른 밸브 각도와 매우 다른 경향을 나타낸다.

Fig. 8

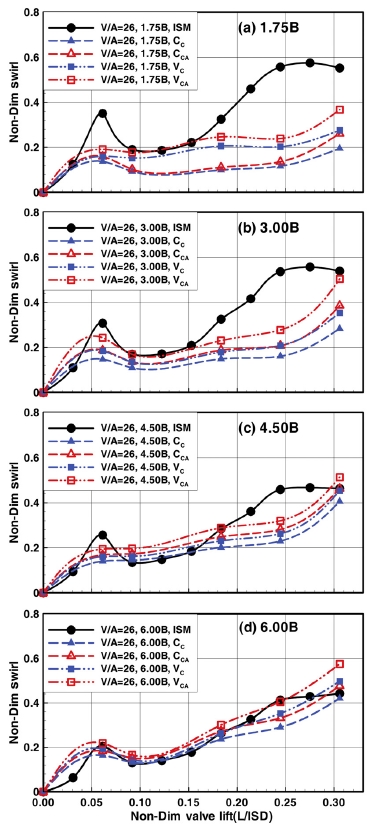
Non-dimensional rig swirl as a function of non-dimensional valve lift according to evaluation position when V/A=26°

앞의 경우에서는, 축 방향 속도를 고려하면 모든 평가위치에서 스월 값이 크게 나오는데 비해, V/A 26°일 때는 이러한 경향이 나타나지 않는다.

1.75B에서는 스월 중심의 평가가 높고, 리프트 8 mm까지는 축 방향 속도의 영향을 받지 않다가 리프트 10 mm에서만 V_CA와 C_CA가 V_C 및 C_CA보다 유의미하게 높다. 3.00B와 4.50B에서는 C_CA가 C_CA와 거의 같으며 6.00B에서는 미세하지만 오히려 V_C가 C_CA보다 높게 나온다.

이 각도의 운동량 분포를 Fig. 9에 제시하였는데, 앞에서는 리프트 10 mm가 모든 변화를 설명할 수 있는 대표적 경우인데 반해, V/A 26°에서는 리프트에 따른 변화도 크기 때문에 리프트 6 ~ 10 mm를 제시하고 측정 평면은 1.75B와 6.00B만 제시하였다.

Fig. 9

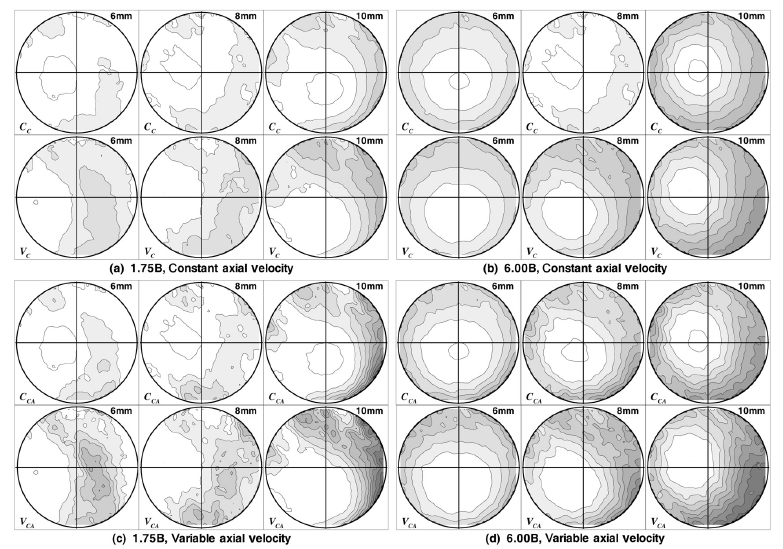
Momentum distribution of V/A 26° port according to evaluation method at high valve lift when 1.75B and 6.00B position

그림에서 관찰할 수 있듯이 속도분포의 영향으로 운동량 분포도 매우 복잡한 형태를 보여주고 동시에 거시적 분포 상태도 매우 다르다.

먼저 1.75B에서, 다른 밸브 각도와 달리 리프트 10 mm에서만 스월 거동에 가까운 형태가 관찰된다. 6 mm와 8 mm일 때 C_CA가 V_C보다 스월이 낮은 이유는, C_CA에서는 편심이 크기 때문에 축 방향 속도가 빠른 영역이 실린더 중심에 가까워 운동량이 낮게 평가되고 반면에 V_C는 편심에 의한 거리 증가의 효과로 운동량이 높게 평가되기 때문이다. 10 mm에서는 다른 각도에 비해 왜곡은 심하지만 스월 거동이 존재하여, 실린더 중심에서 먼 벽면 근처의 운동량이 증가하여 C_CA가 급격히 증가하지만, 이 영역의 면적이 충분치 않아 V_C보다는 낮다.

6.00B에서는 여전히 복잡한 분포를 보여주지만 1.75B에 비해서는 비교적 스월 거동의 형태가 뚜렷이 나타난다. 그럼에도 1.75B의 10 mm와 마찬가지로 C_CA 평가에서 실린더 벽 부근의 운동량은 V_C보다 증가하지만 전체적으로 그 면적이 크지 않아 V_C보다 낮게 평가된다.

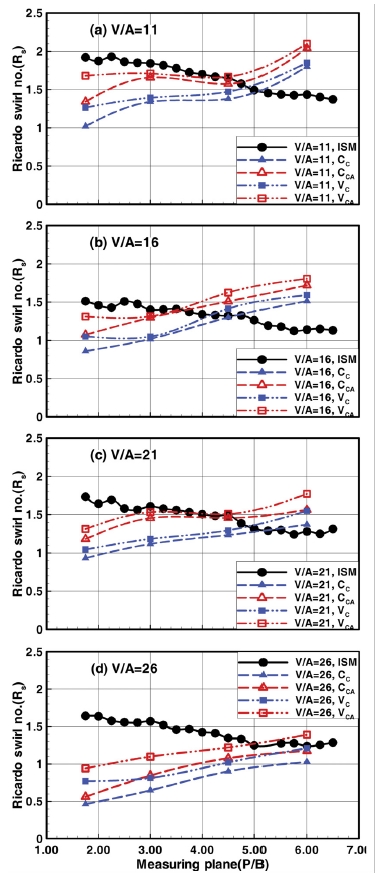
Fig. 10은 식 (5)를 이용해 각각의 평가 방법에 따라 정상유동평가의 최종 도출 값인 스월 비(R_s)를 밸브각도 별로 평가위치에 따라 나타낸 것이다.

Fig. 10

Swirl ratio as a function of evaluation position according to evaluation method

평가 위치에 따른 변화는 역시 이전 연구⁵⁾에서 자세히 논의하였으므로, 축 방향 속도가 평가에 미치는 영향에 주목하여 논의하면 다음과 같다.

전체적으로 축 방향 속도의 영향은, 예외적인 경향을 나타내는 V/A 26°를 제외하면 비교적 단순하게 나타난다. 즉 중심 설정이 동일한 경우 평가 위치에 따른 변화의 경향은 동일하고 다만 축 방향 속도를 고려할 때 일정 수준 높은 값을 유지한다. 따라서 ISM 평가 값보다 더 높게 평가되는 위치가 V/A 11°~ 21°는 축 방향 속도가 일정한 경우보다 더 상류에서 나타나며, 26°의 경우에도 6.00B에서는 V_CA 평가가 ISM보다 높다.

밸브 각도별로 살펴보면, 11°의 경우 3.00B에서 C_CA가 급격히 증가하여 V_CA와 거의 같아지고, 이후 4.50B에서 C_CA와 V_CA가 모두 소폭 감소하여 ISM 평가와 매우 근접한 경향을 보이다가 6.00B에서 급격히 증가한다.

16°에서, 스월 중심인 V_C와 V_CA는 3.00B로 이동하며 거의 값에 차이가 없지만, 실린더 중심인 C_C와 C_CA는 증가하여 축 방향 속도에 의한 차이만 존재한다. 이후 하류로 갈수록 PIV 기반 평가는 직선적으로 증가하여 4.50B 이후에는 ISM 보다 높으며 또한 중심 설정에 따른 차이가 다시 나타난다.

21°의 경우 4.50B까지 중심 설정에 따른 차이가 근소하게 유지되며 주로 축 방향 속도의 차이만 관찰된다. 또한 11°에서와 같이 3.00 ~ 4.50B 사이에서 축 방향 속도를 고려한 경우 ISM과 매우 잘 일치한다. 6.00B로 가면서 PIV 평가는 증가하지만 예외적으로 C_C의 증가가 적다.

26°의 PIV 평가는 대체로 하류로 가면서 직선적으로 증가하는 경향이 있고, ISM과 PIV 평가의 차이가 가장 크게 나타난다. 그리고 앞서 언급한 바와 같이 6.00B에서는 V_CA 평가만 ISM보다 높다.

현재까지 중심 설정과 축 방향 속도 분포 가정이 스월의 평가에 미치는 영향을 검토하면서, 일부 예외적인 경우를 제외하면 축 방향 속도의 영향이 중심 설정보다 크게 나타나고, 3.00 ~ 4.50B 구간에서 ISM과 PIV의 평가가 교차한다.

한편, 축 방향 유동이 본 연구에서 가정한 두 가지 형태에 가깝다면, 평가위치에 따른 ISM 평가는 C_C또는 C_CA와 매우 유사한 값과 형태를 보여주어야 한다. 그러나 실제로는 평가위치가 하류로 갈수록 ISM 평가는 지속적으로 감소하고 반면 PIV 평가는 증가하는데, 이러한 것은 실제 축 방향 속도분포가 본 연구의 가정에서 벗어나는 부분이 있음을 의미한다. 이러한 관점에서 속도 분포, 운동량 및 스월계수와의 관계를 종합적으로 검토할 필요가 있다.

일단, 개별 유동 요소는 일정 기준 단면에서 서로 다른 운동량을 가지고 있지만, 큰 규모의 유동이 존재하여 전개될 때 각 미세요소 사이의 운동량 교환은 제한적이므로 특정 요소의 운동량은 대체로 유지된다고 볼 수 있다. 따라서 밀도에 차이가 없는 한 특정 요소의 속도는 위치에 따라 변화가 거의 없다. 이러한 조건하에서 흡입유동이 실린더 내에서 진행할 때 여러 가지 상황이 발생할 수 있다.

이를 Fig. 11에 제시한 V/A 11°와 26°에서 축 방향속도를 측정한 결과와 , Fig. 12에 제시한 CI 기관을 대상으로 한 해석 결과를 참조하며 논의하면 다음과 같다.

Fig. 11

Velocity profile of vertical plane from 0 to 1.00B

Fig. 12

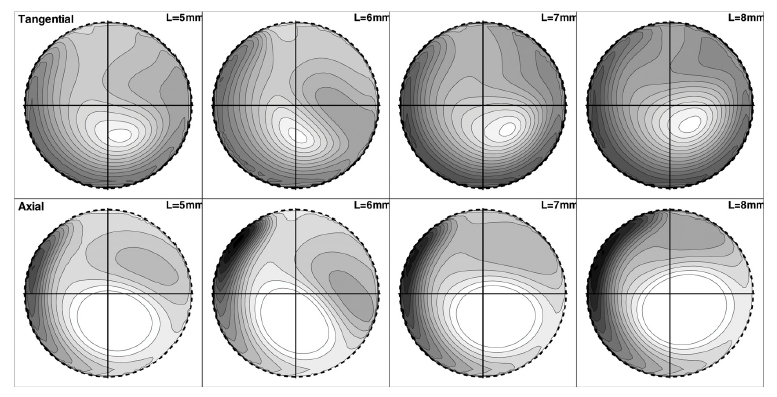
Tangential and axial velocity distribution of CI port at 1.75B position (Numerical analysis, Inner area of first contour line in axial velocity is reverse flow region)

먼저 전체적인 속도 분포를 보면, 접선과 축 방향속도 분포는 Fig. 12에서 볼 수 있듯이 상당히 유사하며, 두 방향의 속도가 비례한다는 본 연구의 가정에서 크게 벗어나지는 않는다.

그러나 운동량이 보존되는 특정 유동 요소가 실린더 내에서 진행하면서 다른 위치에 도달한 경우에는 또 다른 측면을 고려해야 한다. 구체적으로, Fig. 11에서 관찰되듯이 유동은 실린더 벽과 접촉하며 진행하면서 방향이 크게 변한다. 이 때 운동량이 보존되어 특정 유동 요소의 절대 속도가 변하지 않는다면 받음각에 따라 접선속도와 축 방향 속도 사이에는 멱함수 관계가 성립된다(Fig. 13).

Fig. 13

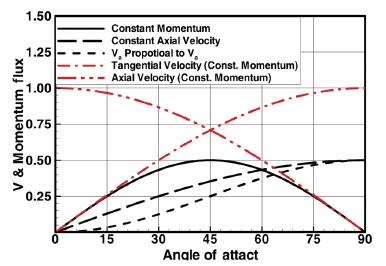
Momentum flux evaluation of flow element and velocity fractions as a function of attack angle to measuring plane under momentum conservation

한편, 스월 계수는 운동량의 비로 정의되지만, ISM으로 운동량의 직접 측정은 불가능하므로 유동의 토크 즉 접선 방향 운동량 모멘트의 유속(Moment of momentum flux)을 측정하여 각운동량(Angular momentum)을 추정한다. Fig. 13(a)에서 운동량이 보존되는 경우 받음각 또는 접선속도 비율에 따른 축 방향 속도와 운동량 유속과의 관계를 볼 수 있다.

마지막으로 Fig. 11의 전후 평면의 중심 단면(Front-rear plane center)에서 재순환류가 관찰되고, Fig. 12의 축 방향 속도 분포에 대한 그림 설명에 나타내었듯이 유동 중심에서부터 첫 번째 등고선 안쪽도 축 방향 속도가 상류를 향하는 역류인데, 이 역시 재순환류에 의한 것으로 판단된다.

이러한 운동량 보존 조건 하에서 실린더 내 유동이 전개될 때, 속도분포 변화 및 운동량 변환이 ISM 측정과 스월 계수에 미치는 영향을 검토해 본다.

만일 측정 평면이 이동하여 유동 전개에 따라 측정 평면에 진입하는 특정 요소의 받음각이 변하는 경우 유동이 가진 전체 운동량에는 변함이 없어도 접선 방향의 운동량은 변화한다. 즉 운동량 변환에 의하여 ISM으로 측정되는 토크는 달라지고 스월 계수는 변하게 된다.

두 번째로 역류가 발생하는 경우, 역류에 의해 접선 유동의 방향은 바뀌지 않으므로 이에 의한 반대 방향의 토크는 발생하지 않는다. 그러나 역류가 발생하면 실린더 벽에 가까운 유동의 축 방향 속도는 역류가 없을 때 보다 상대적으로 더 커져야 한다. 따라서 역류도 ISM 측정 값 증가에 기여하고 동시에 실린더 벽 주위의 축 방향 속도 증가도 역시 ISM 측정 값 증가를 야기한다.

이러한 현상은 지금까지 이전연구를 통해 논의해 온, ISM 평가에서 유동의 강체회전과 이에 포함된 축 방향 속도가 일정하다고 가정한 것과 관련되어 있다. 이전 연구에서는 주로 실제 속도분포는 ISM에서 가정한 이상적 분포와 상당히 다르고, 동시에 평가위치가 하류로 갈수록 어느 정도 이상적 분포에 근접해 간다는 것을 관찰되었다.

한편 본 연구에서와 같이 축 방향 속도를 고려하면, 실제 유동구조는 ISM에서 가정한 유동구조보다 훨씬 더 복잡하며 동시에 평가 위치에 따라 변화가 발생하면 각운동량도 상당히 달라지고, 각운동량의 합도 변화한다. 이때 유동은 하류로 진행하면서 전개하므로, 하류로 갈수록 받음각에 의한 변동이 감소하며 동시에 역류도 감소하여 ISM 측정값은 감소한다. 이를 Fig. 10에 제시한 ISM 및 PIV 측정값의 변동과 연관하여 추론하면 다음과 같다.

ISM의 경우 5B 근방까지는 측정위치가 하류로 가면서 측정값의 감소와 변동이 비교적 크게 나타나고, 5B 이후에는 비교적 감소와 변동이 적게 나타난다. 이는 5B 이전에는 유동구조 변화에 의한 운동량 변환과 역류의 효과가 크게 나타나고 ,이후유동 전개에 의해 운동량 변환 효과가 줄어들면서 주로 마찰 등에 의한 영향이 나타난 것으로 판단된다.

PIV의 평가에서는, 접선방향의 유동이 크고 축 방향 유동이 없는 경우 실제로 운동량 모멘트 유속은 없지만, 본 연구의 가정에 의해 평가하면 Fig. 13에서와 같이 이 부분이 과도하게 평가된다.

그러나 이러한 극단적 유동은 상류에서 두드러지고, 하류로 가면서 유동 구조 변화에 의해 접선 또는 축 방향 속도 속도가 감소하고 대신 축 방향 속도가 증가하면 이 유동 요소의 운동량 모멘트 유속은 감소하지만, 반대로 축 방향 속도만 가진 유동 요소도 접선 방향 속도를 가지게 되어 이러한 감소를 상쇄한다. 동시에 이전 연구에서 고찰하였듯이 유동의 구조가 점차 이상적인 형태로 바뀌어, 실린더 중심에서 먼 벽 주위에 운동량이 큰 부분의 면적이 넓어지면서 추가로 평가 값은 증가한다.

이후 후속 연구에서는 반경 방향을 따른 운동량과 누적 운동량 등의 분석을 통해 편심과 속도 분포 그리고 축 방향 속도의 영향에 대해 정량적 분석을 하겠다.

4. 결 론

밸브각도가 다른 네 가지 헤드를 대상으로 PIV측정을 기반으로 축 방향 속도가 스월에 미치는 영향을 고찰한 결과 다음과 같은 결론을 얻었다.

1) 축 방향 속도의 영향이 평가중심 설정의 영향보다 크다
2) 축 방향 속도를 고려하면 중심 주변의 운동량 감소보다 실린더 벽 주변의 증가가 훨씬 크기 때문에 스월 계수가 증가한다.
3) 접선과 축 방향 속도 분포는 상당히 유사하지만, 축 방향으로는 재순환에 의한 역류도 존재하여 측정값을 왜곡시킨다.
4) 운동량이 보존되는 유동인 경우, 유동구조 변화에 의한 운동량 변환에 의해 측정평면 위치에 따라 ISM으로 측정되는 스월 계수는 변하게 된다.
5) ISM 평가에서 5B 이전에는 유동구조의 변화와 역류의 효과가 크게 나타나고 이후에서 유동전개에 의해 구조 변화가 줄어들면서 주로 마찰 등에 의한 효과가 지배적 역할을 한다.
6) PIV의 평가에서는, 하류로 진행하면서 받음각 변화 효과는 접선 및 축 방향 유동이 서로 상쇄하여 나타나지 않고 유동의 구조가 점차 이상적인 형태로 바뀌어 평가 값이 증가한다.

Nomenclature


B :	cylinder bore, m
C_f :	flow coefficient
ISD :	inner seat diameter
D :	inner valve seat diameter
M :	momentum
$m ̇$ :	mass flow rate through port, kg/sec
N_r :	non-dimensional rig swirl
n :	number of intake valve
R_s :	swirl ratio
r :	distance from center to element area
S :	engine stroke
T :	moment of momentum flux, N․m
$υ ̅$ :	average planar velocity
υ₀ :	theoretical velocity through port, m/sec
υ_θ :	tangential velocity, m/sec
υ_z :	axial velocity, m/sec
υ_x :	velocity(cartesian coordinate), m/sec
υ_y :	velocity(cartesian coordinate), m/sec
α₁ :	crank angle intake valve opening, rad
α₂ :	crank angle intake valve closing, rad
ρ :	density of air, kg/m³

Acknowledgments

이 연구는 서울과학기술대학교 교내연구비의 지원으로 수행되었습니다.

References

C. J. Park, and I. Y. Ohm, “Study on Evaluation Method of Flow Characteristics in Steady Flow Bench(1)-Raising Issue”, Transactions of KSAE, 23(1), p88-96, (2015).
C. J. Park, and I. Y. Ohm, “Study on Evaluation Method of Flow Characteristics in Steady Flow Bench(2)-Comparison of ISM and PIV Measurement”, Transactions of KSAE, 23(1), p139-147, (2015).
C. J. Park, J. Y. Sung, and I. Y. Ohm, “Study on Evaluation Method of Flow Characteristics in Steady Flow Bench(3)-Velocity Profile(1)”, Transactions of KSAE, 24(2), p169-182, (2016).
C. J. Park, J. Y. Sung, and I. Y. Ohm, “Study on Evaluation Method of Flow Characteristics in Steady Flow Bench(4)-Velocity Profile(2)”, Transactions of KSAE, 24(2), p242-254, (2016).
S. H. Cho, and I. Y. Ohm, “Study on Evaluation Method of Flow Characteristics in Steady Flow Bench(5)-Effect of Evaluation Position”, Transactions of KSAE, 25(2), p179-189, (2017). [https://doi.org/10.7467/ksae.2017.25.2.179]
J. B. Heywood, Heywood, Internal Combustion Engine Fundamentals, Int. edn., McGraw-Hill, Singapore, p343-345, (1988).
R. Stone, Introduction to Internal Combustion Engine, 2nd edn., McGraw-Hill, Hong Kong, p183-185, (1992).

Common
Valve angle (°)		11, 16, 21, 26
Bore (mm)		86
Valve lift (mm)	ISM	1~10, 1 mm increment
Valve lift (mm)	PIV	2, 3, 6, 8, 10 mm
Measuring position		1.75, 3.00, 4.50, 6.00 B
Pressure drop		15" H₂O (383 mmH₂O )
PIV
Laser pulse	Separation	25 μsec
Laser pulse	Frequency	5 Hz
Width		≪100 μm
Raw Data No.		200
CCD Camera		KODAK Megaplus ES 1.0
Lens		85 mm PC-E Micro Nikkor
Processing		50 % Overlap,16 ×16 pixel
Atomizer		TSI_SIX-JET 9306
Particle	Size	≪1 μm
Particle	No. Density	107 particle/cm³
Stokes No.		≪1
Software		TSI_Insight

Method	Center	Axial velocity assumption
C_C	Cylinder	$C o n s t a n t υ z, i = υ ¯ = Q υ / A$
C_CA	Cylinder	$υ z, i = υ z ∙ υ i / υ ¯$
V_C	Swirl	$C o n s t a n t υ z, i = υ ¯$
V_CA	Swirl	$υ z, i = υ z ∙ υ i / υ ¯$