[ Article ]

Transactions of The Korean Society of Automotive Engineers - Vol. 26, No. 1, pp.120-130

ISSN: 1225-6382 (Print) 2234-0149 (Online)

Print publication date 01 Jan 2018

Received 17 Jul 2017 Revised 13 Nov 2017 Accepted 28 Nov 2017

DOI: https://doi.org/10.7467/KSAE.2018.26.1.120

평행축 기어트레인을 갖는 변속기의 마찰 및 쳐닝 동력 손실 예측

박기종^*^{, 1)}

; 강마루¹⁾ ; 이승호¹⁾ ; 손우철¹⁾ ; 권여현²⁾ ; 아멧 칼만³⁾

1)현대자동차 선행변속기개발팀
2)현대자동차 수동변속기설계팀
3)오하이오주립대학교 기계항공공학과

Prediction of Mechanical and Spin Power Losses of a Parallel-Axis Geartrain in an Automobile Transmission

Kijong Park^*^{, 1)}

; Maru Kang¹⁾ ; Sueng Ho Lee¹⁾ ; Woochurl Son¹⁾ ; Yeo Hyeon Kwon²⁾ ; Ahmet Kahraman³⁾

1)Advanced Transmission Development Team, Hyundai Motor Company, 150 Hyundaiyeonguso-ro, Hwaseong-si, Gyeonggi 18280, Korea
2)Manual Transmission Engineering Design Team, Hyundai Motor Company, 150 Hyundaiyeonguso-ro, Hwaseong-si, Gyeonggi 18280, Korea
3)Department of Mechanical and Aerospace Engineering, The Ohio State University, OH 43210, USA

Correspondence to: ^*E-mail: ecjeon@sejong.ac.kr

* This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium provided the original work is properly cited.

Abstract

The automotive industry is currently focusing on the development of a highly efficient gearbox to reduce the fuel consumption of vehicles. A transmission system with a parallel-axis geartrain has higher efficiency than the one with a planetary geartrain. Power losses of the transmission with a parallel-axis geartrain are mainly generated by the gears and bearings. In this study, a process was developed to analyze the efficiency of an entire parallel-axis gearbox, considering the power losses of all the components, such as the gear mesh, gear spin, bearings, and synchronizer. The analytical models that were used were based on the component power loss models developed in previous studies and published in many papers. The process included the power flow analysis of a parallel geartrain. The power losses and transmission efficiency of a few automotive gearboxes with a parallel geartrain were estimated through the process. The results were compared with the experiment data.

Keywords:

Power loss, Mechanical, load-dependent, loss, Spin, load-independent, loss, Parallel-axis geartrain, Gear friction, Gear churning, Bearing power loss

키워드:

동력손실, 마찰 (하중관련) 손실, 회전(하중무관) 손실, 평행축 기어트레인, 기어 마찰, 기어 쳐닝, 베어링 동력 손실

1. 서 론

변속기의 전달효율은 차량의 연비와 직접적으로 관련되어 있어 차량의 연료소모를 줄이기 위하여 변속기 효율을 개선하고 향상시키는 필요성이 대두되고 있다. 최근 연비규제나 환경규제로 인하여 자동차 산업 전반에 걸쳐 연비관련 기술 개발이 이슈로 떠오르고 있다. 변속기 측면에서도 전달효율관련 문제가 주요 관심사가 되었다. 각 회사들은 시스템의 동력손실을 예측하고 계산하여 향상된 전달효율을 갖는 시스템을 개발하고 설계하는데 집중하고 있다. 따라서 변속기 개발 프로세스에서 변속기 전달효율 예측과 해석은 매우 중요한 전략기술이 되고 있다.^1-8)

기존의 수동변속기에서 외접 기어쌍의 조합으로 기어비를 만드는 외접기어트레인이라고도 불리는 평행축 기어트레인(Parallel-axis geartrain)은 기존의 자동변속기에서 유성기어의 조합으로 기어비를 만드는 유성 기어트레인(Planetary geartrain)과 같이 승용차용 변속기 기어트레인 구조로 널리 사용되고 있다. 최근 들어 자동변속기 시장에서도 전달효율측면에서 유리한 수동변속기 구조를 개량하고 이를 자동화한 DCT(Double Clutch Transmission)나 AMT(Automated Manual Transmission)를 도입하는 사례가 늘어나고 있다. 전기차 등에서도 유성기어 트레인에 비해 간단하면서도 효율이 좋은 평행축 구조의 기어트레인이 널리 사용되고 있다. 평행축 구조의 기어트레인에서의 전달효율은 대부분 기어나 베어링에 의한 손실로 나타난다.

과거에는 변속기 전달효율이나 부품 동력손실에 대해서 시험 결과를 바탕으로 한 시험식이나, 회기분석을 통한 동력손실 예측 기법들이 많이 사용되어 왔다.^6,7,9) 최근에는 컴퓨터 처리기술이나 시뮬레이션의 발전으로 많은 시험 결과 데이터나 CFD 등의 대형 시뮬레이션을 통한 수학적 모델을 개발하여 다양한 오일특성이나 오일 온도, 부품의 제원 등에 대해 적용해서 변속기 시스템의 전달효율을 개선하고, 더 나아가 최적화하려는 노력도 보이고 있다.^3-5,7) 기어쌍의 미끄럼 손실이나 구름 손실은 시험환경이나 기어 제원에 한정된 시험결과를 바탕으로 한 과거의 시험식에서 벗어나 Li와 Kahraman¹⁰⁾은 EHL(Elasto-hydrodynamic lubrication) 기법을 이용한 기어 Mechanical efficiency 모델을 발표하였다. Seetharaman과 Kahraman¹¹⁾은 기어 오일 쳐닝에 의한 회전손실(Spin losses)에 대하여 발표하였다.

본 연구에서는 평행축 기어트레인의 부품별 최신동력손실 해석 기법 이론^8-14)을 소개한다. 해석기법의 신뢰성을 검증하기 위하여 전달효율이 기어트레인의 동력손실에 의해서만 계산되는 수동변속기, DCT 및 전기차용 감속기에 적용한 사례에 대하여 보이고 논의한다.

2. 변속기 전달효율과 기어트레인 부품 동력손실

2.1 변속기 전달효율

변속기에서 동력손실을 줄임으로써 변속기 효율증대를 꾀할 수 있다. 일반적으로 승용차에서 많이 사용되고 있는 변속기의 효율은 수동변속기에서 92 ~ 97 %, 자동변속기에서 90 ~ 95 %, CVT에서 약 80 ~ 93 % 정도로 알려져 있다.³⁾ 기존에 많은 경우 변속기 효율은 운전 속도나 하중에 따라 동력손실이 차이가 남에도 불구하고 이러한 참고를 통하여 일정하게 가정하여 사용되어 왔다. 이는 변속기가 차량의 운전조건에서 내연기관과 비교하여 매우 높은 효율을 보이기 때문에 큰 문제는 없었다. 그러나 최근의 개발환경에서 변속기의 적은 손실 또한 개선하고 최소화하려는 노력이 나타나고 있다.^4,8)

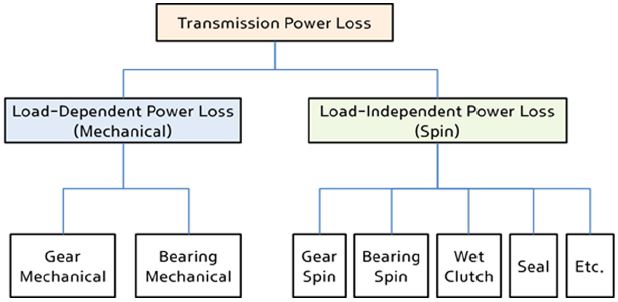
보통 수동변속기나 자동변속기의 동력 손실은 기어의 마찰, 쳐닝, 베어링, 습식클러치, 씰, 오일펌프 등 다양한 경로를 통하여 나타난다. Fig. 1에 나타낸 것처럼 이러한 손실 경로는 크게 하중 즉 토크에 관련된 손실과 토크에는 무관하고 속도에만 관련된 손실로 파악할 수 있다. 일반적으로 전자를 하중관련 손실(Load-dependent power losses) 또는 기계적 손실(Mechanical power losses)이라 하고, 후자를 하중에 무관한 손실(Load-independent power losses) 또는 회전 손실(Spin losses)라고 한다. 하중관련 손실은 기어나 베어링과 같이 압력 하에 있는 두 표면이 서로 상대운동을 할 때 발생되며, 하중이나 미끄럼 속도, 오일 유막에 관련된 마찰계수에 관련되어 있다. 반면 하중에 무관한 회전손실의 경우 기어의 쳐닝뿐만 아니라 클러치나 씰 등과 같이 변속기의 하중경로 상의 토크가 없음에도 불구하고 물체의 회전에 의해서만 발생된다. 기어나 베어링의 경우 마찰손실과 회전손실를 동시에 가지며 기타 나머지 대부분의 부품들은 회전에만 관련된 회전손실을 갖는다.

Fig. 1

Power losses in an automobile transmission

본 연구에서 다루는 평행축 기어트레인을 갖는 변속기 총 동력 손실[W]은 다음과 같이 나타낼 수 있다.

P L = P g m + P g s + P b m + P b s + P j s + P m i

(1)

여기서 P_gm 은 기어 마찰 손실(Mechanical loss), P_gs는 기어 회전 손실(Spin loss), P_bm 는 베어링 마찰 손실, P_bs 는 베어링 회전손실, P_js 는 저널베어링 또는 싱크로나이저 손실을 나타내고, P_mi는 회전마찰이나 기타 손실을 나타낸다. 전체 변속기에서의 전달효율은 다음과 같이 정의할 수 있다.

η = P o u t p u t P i n p u t × 100 = P i n p u t - P L P i n p u t × 100

(2)

여기서 P_input [W] 은 변속기로 입력되는 동력, P_output [W] 은 변속기에서 출력되는 동력이며 전달 효율 η[%] 는 주로 백분율로 표시한다.

2.2 평행축 기어트레인 부품 동력 손실

2.2.1 기어 마찰 동력 손실(Mechanical power loss)

가장 일반적인 기어 효율에 관한 기존의 오래된 모델들⁸⁾은 일정하거나 평균적인 마찰계수 하에서 기어접촉 선상에 균일한 하중이 작용한다고 가정한 이론에 기초하고 있다. 이들 모델들은 대부분 시험식을 바탕으로 손실을 계산하고 있어 시험에서의 기어제원이나 당시 사용한 오일의 특성에 한정된 경우로 좁은 구간에서의 정확성을 보인다. 기어에서 고효율이나 기어 효율의 정확한 효율계산이 필요하지 않았던 과거의 경우에는 상당부분 유용한 모델로 인정받아 왔으나, 현재의 기어 개발 상황에서는 보다 더 정확한 기어효율 예측을 통한 고효율 기어의 개발 필요성이 대두되었다.⁸⁾ 따라서 기어의 물림위치에 따른 하중분포나 마찰계수의 분포를 구하는 것이 보다 정확한 기어 손실을 예측하는데 필요하다.

하중에 의한 기어 손실은 한 피치 내의 기어의 물림점에서 마찰계수, 하중, 속도의 변화로 인해 변하게 된다. 이때 평균 기어 동력손실은 평균 기어 미끄럼 손실(P_gS)과 평균 구름 손실(P_gR)의 합으로 표현할 수 있고 이를 수식으로 나타내면 다음과 같다.

P g m = P g S + P g R

(3)

P g S = 1 L a ∫ 0 L a ∑ i μ l F N l i V s l d l

(4)

P g R = 1 L a ∫ 0 L a P R l b L l d l

(5)

여기서, L_a는 접촉길이 [m] , μ(l) 는 접촉경로(l ≤ L_a) 상의 마찰계수, F_N (l)_i는 접촉경로상의 i번째 물림치에 작용하는 법선 하중 [N] , V_s(l)은 미끄럼 속도[m/s] 이고, P_R (l)은 접촉경로상의 구름 손실 밀도[W/m² ] , bL(l)은 접촉경로(L(l))에 치폭(b)를 곱한 모든 유효한 물림치를 위한 접촉면적 [m² ]이다. 기어 물림위치에 따른 하중분포나 마찰계수, 구름 손실 밀도 등의 보다 정확한 수식이나 수치적 계산 방법은 참고문헌[8]을 통하여 알 수 있다.

2.2.2 기어 회전 동력 손실(Spin power loss)

기어의 회전손실은 Windage 손실, Churning 손실, Pocketing 손실 등의 3가지의 주요 요인이 있다. Windage 손실은 오일에 잠겨 있지 않는 기어가 회전하면서 공기나 공기 중에 비산된 오일 Mist에 의해 나타나는 손실이다. Churning 손실은 변속기 내부의 오일 속에 잠겨있는 기어의 회전을 방해하는 손실이다. Pocket 손실은 고속의 기어 물림에서 오일이 기어치 사이에 압축상태로 끼어서 기어 회전을 방해하는 손실로 주로 평치차(Spur gear)에서 나타나고 구조상 헬리컬 기어에서는 아주 미미한 값을 갖는다.

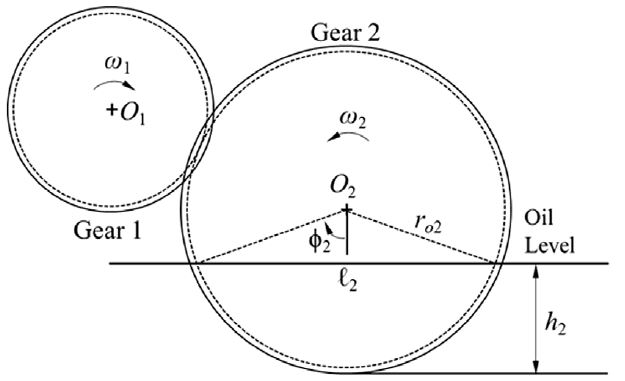
최근 Seetharaman과 Kahraman¹¹⁾은 기어에서의 무부하 회전 동력손실에 관한 연구를 발표하였다. 그들은 Fig. 2와 같이 부분적 또는 완전히 오일에 잠겨있는 기어에서 드래그 손실은 다음과 같이 세개의 개별 손실의 합으로 나타내었다.

Fig. 2

Parameters of a gear pair immersed in the oil

P g s = P d p + P d f + P r f

(6)

P_dp [W] 는 기어의 외주(Periphery)에 작용하는 오일이나 공기의 드래그 토크에 의한 동력손실로 기어 속도, 오일점도, 기어경의 크기, 치폭 및 잠김율에 의해 나타난다. 기어 i의 외주에서의 드래그에 의한 동력 손실은 다음과 같다.

P d p i = 4 μ 0 b i r o i 2 ω i 2 ϕ i

(7)

여기서, ϕ_i = cos^-1 [(r_oi - h_i )/r_oi ] 은 기어 잠김각이다.

P_df [W] 는 기어의 옆면(Face)에 작용하는 드래그 토크에 의한 동력손실로 오일의 특성, 기어속도, 반경에 의한 레이놀즈 수(Re = 2ρω_ir_oi² /μ₀ )에 따라 층류(Laminar flow)와 난류(Turbulent flow) 모델로 각각 다음과 같이 나타낼 수 있다.

P d p i L = 0.41 ρ μ k 0.5 ω i 2.5 r o i 2 A d f i sin ⁡ ϕ i R e ≤ 2 × 105

(8)

P d p i T = 0.025 ρ μ k 0.14 ω i 2.86 r o i 2.72 A d f i sin ⁡ ϕ i 0.14 R e ≤ 2 × 105

(9)

여기서, A_dfi = ϕ_ir_oi² - (r_oi - h_i )r_oisinϕ_i 는 기어 측면 잠김 면적[m²]이다.

마지막으로 P_rf[W] 는 기어치가 오일을 쓸고 가는 것에 의해 작용하는 드래그 토크에 의한 동력 손실이다. 기어가 부분적으로 오일 속에 잠겨있을 때, 인접한 치사이의 공간은 오일에 잠긴 잇수 만큼 오일이 채워진다. 이런 공간은 빠른 속도로 기어가 회전할 때, 오일 온도가 높으면 즉 오일 점도가 낮으면 완전히 채워지고, 오일온도가 낮으면 오일의 점도로 인해 부분적으로 채워지는 현상을 볼 수 있다. 이를 미분방정식으로 모델링하고 경계조건을 적용하여 풀면 다음 식과 같은 동력 손실 식을 얻을 수 있다.

P r f i = 2 n i μ 0 A c ω i r o i - r r i C 1 i r o i r r i - C 2 i

(10)

여기서, 오일에 잠겨있는 치의 개수는 n_i = int(Z_iϕ_i/π)이고, 기어 치사이의 공간의 면적은 A_c =π/2Z_i (r_oi² - r_ri²)[m² ]이다. 적분계수는 C_1i =- -2ω_ir_oi²r_ri²(r_oi² - r_ri2)(ln r_oi - ln r_ri)/[4r_oi²r_ri² (ln r_oi - ln r_ri )² ] 와 C_2i =- ω_i (r_oi² - r_ri²)²/[(r_oi² - r_ri²)² - 4r_oi²r_ri²(ln r_oi - ln r_ri)²]로 나타낼 수 있다.

기어가 회전할 때, 기어 쳐닝에 의해 오일은 공기중으로 비산되어 안개처럼 비산된다. Fig. 2에서 Gear 1과 같이 오일에 잠겨 있지 않은 기어들은 이러한 공기-오일에 의해 드래그가 발생하게 된다. 비산된 오일에 의한 공기-오일 Mist 모델은 혼합유처럼 오일 특성을 변화시켜 표현할 수 있다. 공기-오일 Mist의 밀도는 다음과 같이 나타낼 수 있다.¹²⁾

ρ m i s t = ψ ρ o i l + 1 - ψ ρ a i r

(11)

여기서, ψ = V_oil/(V_oil +V_air ) 는 공기-오일 Mist의 부피비이다. 혼합 Mist의 절대 점도는 다음과 같다.

μ 0, m i s t = χ μ 0, a i r + 1 - χ μ 0, o i l

(12)

여기서, χ = (1/ρ_mist - 1/ρ_oil )/(1/ρ_air - 1/ρ_oil ) 로 나타낼 수 있고, 동점도는 μ_k,mist = μ_0,mist/ρ_mist 로부터 구할 수 있다. 이렇게 변화된 물성을 이용하여 기어의 외주와 측면에서의 동력 손실을 식 (7)과 식 (8)로부터 구할 수 있다.

2.2.3 베어링 동력 손실

일반적으로 자동차용 변속기의 축지지용 베어링은 볼베어링, 롤러베어링, 테이퍼롤러베어링 등이 주로 사용되고 있으며, 축과 축, 기어와 축사이에 니들롤러베어링이 사용되고 있다. 베어링의 손실은 기어에서 작용하는 하중을 축을 통해 지지하므로 하중에 관련된 마찰 토크 손실로 나타나고, 유체나 그리스내에서 축이나 케이스에 대해 회전 저항을 발생시키고 이는 회전 손실로 나타나게 된다.¹³⁾ 따라서 베어링 토크 손실(T_b,[Nm] )은 보통 시험식을 통하여 일반화되고, 다음식과 같이 경방향 하중에 의한 토크 손실(T_radialL,[Nm] )과 축방향 하중에 의한 토크 손실(T_axialL,[Nm] ), 오일에 의한 토크 손실(T_oil,[Nm] )로 나타낼 수 있다.¹⁴⁾

T b = T o i l + T r a d i a l L + T a x i a l L

(13)

오일에 의한 토크 손실은 오일특성과 속도에 의한 유동에 의해 다음과 같이 표현된다.

T o i l = f 0 d m 3 μ k ω 2 / 3 9.78 × 10 - 2

(14)

여기서, f₀는 베어링 타입과 윤활 방법에 따른 상수이며, 층류와 난류의 유동 특성을 나타내는 μ_kω ≤ 2000의 값을 갖는다.

하중에 의한 베어링 손실은 경방향 하중과 축방향 하중의 조합에 의한 손실(T_radialL)과 롤러베어링이나 테이퍼 롤러베어링 등에서의 베어링 립(Lip)에서 발생하는 손실(T_axialL)로 다음과 같이 나타낼 수 있다.

T r a d i a l L = f 1 P 0 + P 1 d m

(15)

T a x i a l L = f 2 F a d m

(16)

여기서, f₁ 과 f₂ 는 베어링 하중 상수, P₀는 등가예하중(Equivalent static preload), P₁은 등가동하중(Equivalent dynamic load)으로 축방향 하중(F_a,[N] )과 경방향 하중(F_r,[N])의 비로 주어진다.

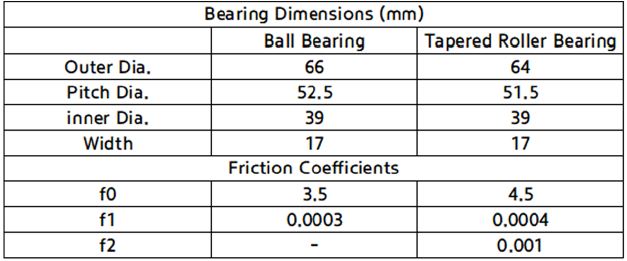
베어링 동력손실을 변속기 내부 작동조건에서 예측하는 것은 실제로 매우 어렵다. 앞서 설명한 일반적인 베어링 토크손실 식인 식 (14) ~ 식 (16)을 이용하면 베어링 상수인 f₀ , f₁와 f₂가 여전히 미지수로 남는다. 일반적으로 베어링 회사에서는 카탈로그 등을 통해 베어링의 타입과 치수별로 각 상수 값들을 제공하고 있지만, 보다 정확한 값의 예측을 위해서는 단품 시험 결과로부터 구하는 것이 필요하다. Fig. 3은 Table 1에 나타낸 볼 베어링과 테이퍼 롤러베어링에 대한 단품시험 결과와 식 (14) ~ 식 (16)의 결과가 시험결과와 일치하도록 베어링 상수를 찾았을 때의 해석 결과를 나타내고 있다. Table 1에 그 때 얻은 베어링 상수를 볼 베어링과 테이퍼 롤러 베어링에 대해서 각각 나타내었다.

Fig. 3

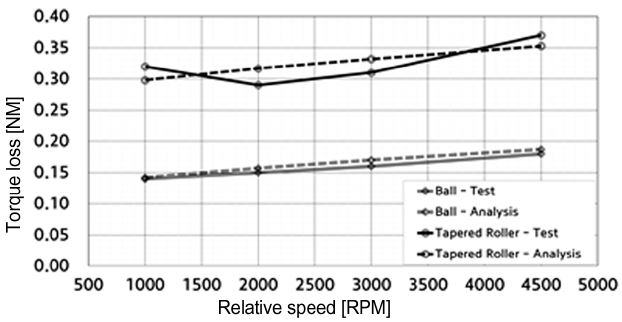
Bearing torque loss correlation between test and analysis results to find the coefficients f0 , f1 and f2

Table 1

Bearing dimensions and friction coefficients obtained by test-analysis correlation

2.2.4 싱크로나이저 동력 손실

평행축 기어트레인에서 선택적 동력흐름의 변화, 즉 변속단을 형성하는 요소로 싱크로나이저가 흔히 사용된다. 일반적인 평행축 기어트레인인 수동변속기나 DCT에서 차량 관성이 연결된 출력축의 회전속도와 클러치를 포함한 입력축과의 상대 속도를 일치시키는 장치를 싱크로나이저라고 한다. 따라서 비개합(Open) 상태에 있는 싱크로나이저는 마찰재가 붙어 있는 허브측의 링과 아이들 기어측의 마찰면 사이에 유막이 형성되고 양단의 속도차이에 의해 드래그 손실로 작용하게 된다.

싱크로나이저 링과 아이들 기어의 마찰면 사이의 토크손실은 저널베어링의 손실처럼 다음과 같이 계산된다.¹⁴⁾

T j s = f r i n g 2 π μ 0 r i n g 3 l r i n g h r i n g

(17)

여기서, 마찰면에 직각인 간극은 링과 아이들 기어 사이의 축방향 간극(h_axis)과 링의 개수(n_ring ), 싱크로나이저 콘 반각(Cone haf angle, θ)을 이용하여 h_ring = h_axis/n_ringsin (θ) 로 나타낼 수 있다. f_ring은 실제 저널 내부의 그루브 등으로 인한 접촉면의 비를 나타낸다.

싱크로나이저 링과 아이들 기어의 마찰면 사이의 상대 속도 Δω 에 대해 동력손실은 다음과 같다.

P j s = T j s ⋅ ∆ ω

(18)

2.3 평행축 기어트레인 Power Flow 해석

2.3.1 기어트레인 속도

평행축 구조 기어트레인은 평행한 두 축상에 다수의 외접 기어쌍을 배열한 구조로 피니언(G1)과 기어(G2)로 구성된 한쌍의 기어에서 1개의 기어물림(Gear mesh)를 갖는다. 한쌍의 외접기어의 속도방정식은 다음과 같다.

ω G 1 Z G 1 + ω G 2 Z G 2 = 0

(19)

여기서, ω는 각 요소의 절대 속도이고, Z는 기어 잇수이다.

한쌍의 외접 기어물림은 식 (19)에 나타낸 것처럼 1개의 방정식과 2개의 미지수를 갖는다. 따라서 속도 관계식을 풀기 위해서는 추가적인 관계식이 필요하다. 일반적으로 기어트레인 파워플로우(Power flow) 상에 기어와 기어사이에 축으로 연결된 고정연결요소로 표현하거나, 싱크로나이저 등을 통해 선택적으로 연결요소를 사용하여 두 요소 i와 j가 동일한 속도(ω_i - ω_j = 0 )를 갖게 하는 방법을 사용한다. 일반적으로 1자유도 평행축 기어트레인은 N_e개의 외접물림, N_r 개의 강체연결, N_s개의 선택연결요소를 갖고 1개의 입력요소를 갖는다. 기어트레인의 미지수의 개수는 N = N_e +N_r +N_s + 1 로 나타낼 수 있다. 이러한 관계식들을 사용하여 연립방정식을 구성하면 다음과 같이 표현할 수 있다.

A Ω ¯ = B ¯

(20)

여기서, Ω = [ω₁ω₂ω₃ ⋯ ω_n]^T 는 미지수인 속도 벡터이고, $A$ 는 기어물림, 연결요소, 입력 등의 정보를 갖는 N 차원의 정방행렬, B 는 입력 속도를 표현하는 하나 이상의 0이 아닌 요소를 갖는 벡터이다.

2.3.2 기어트레인 토크 및 기어 물림 하중

각 기어쌍에서의 물림하중과 베어링에 가해지는 하중을 구하기 위하여 각 요소들에 걸리는 토크를 계산해야만 한다. 각 요소의 토크는 변속기로 들어오는 입력 토크의 함수로 표현된다. 파워손실이 없다고 가정할 때, 계산된 기어들의 속도를 이용하여 기어쌍 j (Deck j )에서의 동력 평형 방정식은 다음과 같이 나타낼 수 있다.

T G 1 j ω G 1 j + T G 2 j ω G 2 j + ∑ i = 1 i ≠ j N t ∑ k ∑ m T k i / m j ω M j = 0

(21)

여기서, T_G1j와 T_G2j는 j번째 기어쌍에서 각각 피니언과 기어의 외력토크를 나타고, N_t 는 시스템에서 기어쌍(Deck)의 총개수, T_ki/mj는 Deck i의 k요소에 의해 Deck j의 m요소에 가해지는 토크이다.

연결요소를 위한 평형 방정식은 다음과 같다.

T k j / m i + T m i / k j = 0

(22)

피니언과 기어가 입력이나 출력이 아닐 경우 외력토크는 0이어야 한다. 즉 기어쌍 j의 요소 i가 입력이나 출력이 아닌 경우 T_ij = 0 이다. 기어쌍 j의 요소 i가 입력 요소일 때, 입력토크는 T_ij = T_in으로 주어진다. 식 (21) ~ 식 (22)와 입출력을 고려하면, N_ex개의 외접 기어쌍을 갖고 N_conn개의 연결요소를 갖는 기어트레인 시스템은 총 N = 2N_ex + 2N_conn 개의 미지수를 갖고 N개의 연립방정식으로 구성된다.

기어트레인에서 각 기어에 작용하는 외력과 각 연결요소의 토크를 계산하면 각 기어쌍에 작용하는 물림하중을 정적 평형 방정식을 이용하여 구할 수 있다. 기어쌍 j의 개별 요소 k는 정적 평형을 만족해야 하고 회전축에 대하여 벡터형식으로 모멘트 평형식을 나타내면 다음과 같이 표현된다.

T k j + T c o n / k j + r k j × F o j / k j = 0

(23)

여기서, T_mj(m = G1,G2) 는 기어쌍 j의 요소 m에 작용하는 외력토크 벡터, T_con/mj는 기어쌍 j의 요소 m에 작용하는 연결요소의 총합 토크벡터, F_lj/mj는 기어쌍 j에서 기어 m에 물림 상대 기어 l에 의해서 작용하는 축직각 접선 물림 하중벡터이다. r_mj는 기어쌍 j의 기어 m의 중심에서부터 피치점까지의 반경벡터이다.

3. 기어트레인 동력 손실을 고려한 변속기 전달효율 해석

2장에서 설명한 기어트레인 동력손실 수식을 적용하여 평행축 기어트레인인 1단 전기차용 감속기, 5단 수동변속기, 7단 DCT에 대하여 동력손실과 전달효율 해석을 수행하였다.

3.1 전기차용 감속기

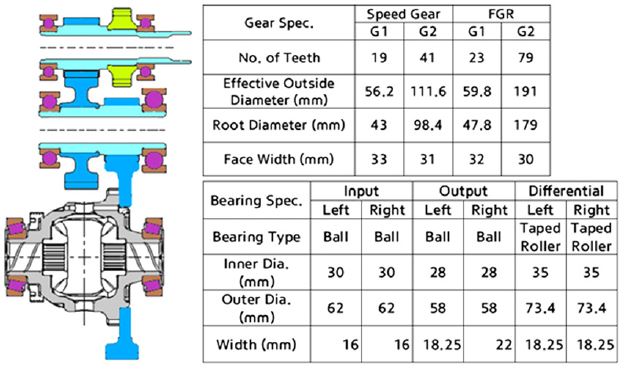
Fig. 4에 나타낸 전기차용 감속기에 대하여 동력손실 및 전달효율 해석을 수행하였다. 감속기는 1단 감속 기어쌍과 종감속 기어쌍으로 구성되어 있다. 기어 제원과 베어링 제원은 Fig. 4와 같다.

Fig. 4

Schematic diagram of a reducer of an EV and the specifications of gears and bearings

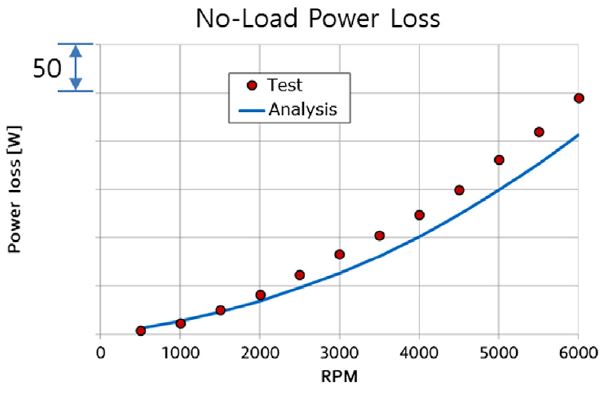
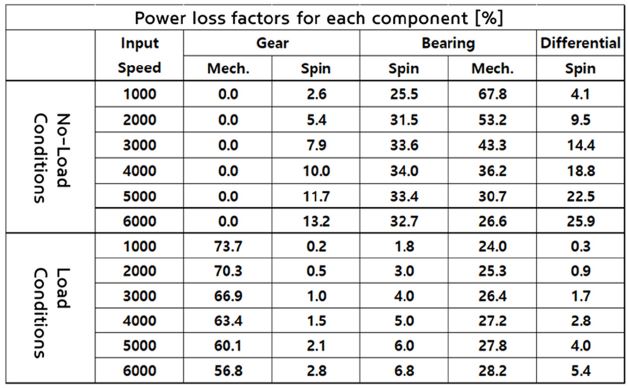
Fig. 5에 70 °C일 때 무부하 동력손실의 시험결과와 해석결과를 비교하였다. 입력 회전속도가 증가함에 따라 무부하 손실이 대략 2차 함수로 증가하는 것을 확인 할 수 있다. Table 2에 나타낸 것 과 같이 무부하 상태에서의 동력손실은 저속일 때, 베어링의 예압의 영향으로 베어링의 마찰 손실이 절대적이며 고속으로 갈수록 베어링과 기어의 회전손실과 차동장치(Differential)의 쳐닝이 매우 커진다.

Fig. 5

Test and analysis results of no-load power loss of the EV gear box

Table 2

The component portion of power losses under no-load and load conditions for the EV gear box

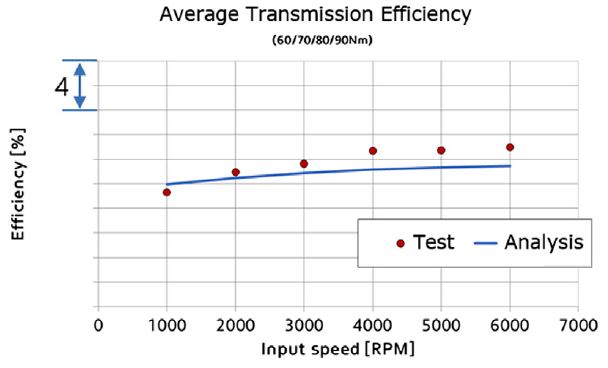
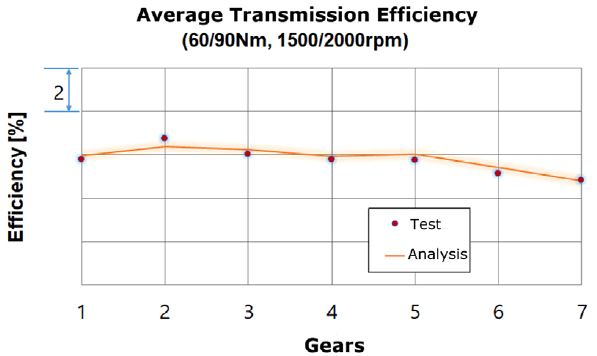
Fig. 6에 70 °C일 때 전달효율 해석 결과와 시험결과를 비교하였다. 입력 토크 60/70/80/90 Nm에서 입력하중에 대한 시험과 해석의 전달효율 결과는 최대 약 0.38 %p 차이로 매우 잘 일치하는 것을 알 수 있다. 이때 전달효율에 영향을 주는 동력손실은 Table 2에서와 같이 기어에서의 마찰 손실이 57~74 %로 가장 크며, 입력 속도가 증가함에 따라 기어의 마찰손실은 줄어들며 베어링에서의 Spin 손실이 24~28 %로 증가하는 것을 알 수 있다. 즉 기어 마찰손실에 대한 최적화가 중요하며, 회전손실을 줄이기 위해서는 베어링의 사이즈와 오일의 점도가 가장 중요하다.

Fig. 6

Comparison of test and analysis results of average transmission efficiency

3.2 전륜 5속 수동변속기

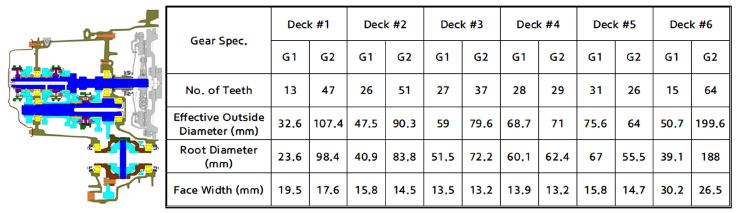
Fig. 7에 나타낸 5속 전륜 수동변속기의 전달효율해석을 수행하였다. 5속 수동변속기의 Speed단의 5개의 기어쌍과 종감속 기어쌍으로 6개의 기어쌍으로 이루어져 있고, Fig. 7에서와 같은 기어제원을 갖는다. 입력축에 2개의 볼베어링(베어링 피치경 dm=45/45 mm), 출력축과 차동축에 각각 2개씩 테이퍼 롤러 베어링(dm=45/42.5/54.2/54.2 mm), 5개의 니들 롤러 베어링(dm=36.5/ 38.3/35/35/35 mm)으로 구성된다.

Fig. 7

Schematic diagram of a 5 speed manual transmission and the specification of gears

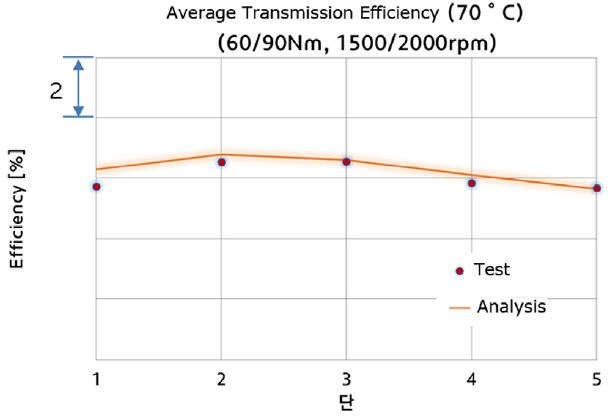
70 °C에서 입력토크 60과 90 Nm, 입력속도 1500과 2000 rpm에 대한 평균 전달효율 해석 결과와 시험결과를 Fig. 8에서 비교하였다. 시험과 해석결과의 오차는 1단에서 최대 오차 0.6 %이고 전단평균과 최고단 전달효율의 55대 45의 조화평균을 취하면, 전달효율 시험과 해석과의 오차는 약 0.1 %p로 매우 잘 일치하는 결과를 얻을 수 있었다. 동력손실 요인으로는 기어의 마찰손실이 가장 크고, 베어링 회전손실 순이었다.

Fig. 8

Comparison of test and analysis results of the 5 speed manual transmission

3.3 전륜 7속 건식 DCT

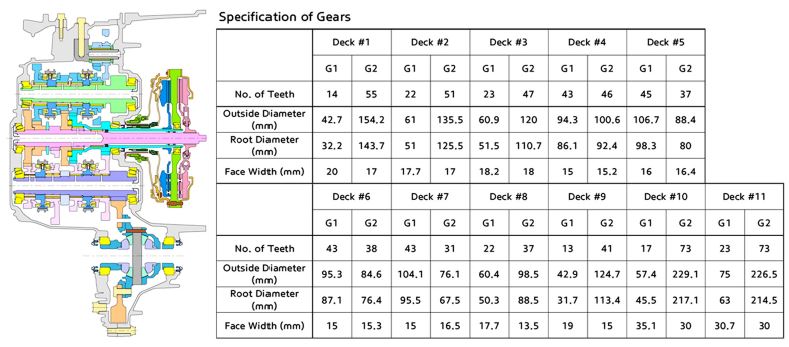
Fig. 9에 나타낸 것과 같이 총 11개의 기어쌍으로 이루어진 건식 전륜 7속 DCT의 전달효율 해석을 수행하였다. Fig. 9에 각 기어들의 제원을 나타내었다. 테이프롤러 베어링 8개, 쓰러스트베어링 1개, 니들롤러베어링 12개, 싱크로나이저를 표현하는 저널베어링 12개를 적용하였다.

Fig. 9

Schematic diagram of a 7 speed DCT and it's gear specifications

70 °C에서 입력토크 60과 90 Nm, 입력속도 1500과 2000 rpm에 대한 평균 전달효율해석 결과와 시험결과를 Fig. 10에서 비교하였다. 각 단별 평균전달효율은 2단에서 최대 0.4 %p, 7단에서 0 %p의 오차를 갖는다. 전단 평균 전달효율로 나타내면 시험과 해석의 차이는 0.1 %p, 고속에 주로 사용되는 최고단의 평균 전달효율로 보면 시험과해석 차이가 0.0 %p, 전단 평균과 최고단 평균 전달효율의 55대 45조화 평균을 취할 경우 시험과해석의 차이는 0.2 %p로 해석 신뢰성을 확보할 수 있었다. 특히 각 단별시험과 해석의 그래프 개형이 거의 일치하는 결과를 얻을 수 있었다.

Fig. 10

Average transmission efficiency of the 7 DCT (Comparison of test and analysis results)

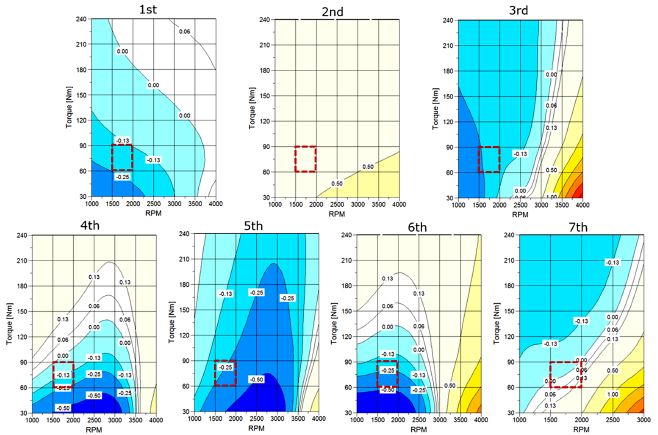
Fig. 11에 입력토크 30 ~ 240 Nm, 입력속도 1000 ~ 4000 rpm에 대한 각 단별 시험 및 해석 결과의 오차를 도시하였다. 전영역 최대 약 3 %의 오차를 보이고, 3단/6단/7단의 저토크, 고RPM영역에서 다소 큰 오차를 보이고 있다. 이는 토크에 의한 기어 마찰손실에 대한 손실계산 식보다 기어나 베어링의 회전손실에 대한 계산 식의 정확성이 다소 미흡한 것으로 판단된다.

Fig. 11

Difference maps between analysis and test results of the transmission efficiency for the 7 speed DCT in the domain of the input torque and speed

4. 결 론

연비규제가 점점 강화되고 있는 상황에서 전달효율 향상을 위한 변속기 설계는 매우 중요하다. 특히 전달효율의 이점을 갖는 평행축 기어트레인을 사용하는 수동변속기나 DCT, AMT 등은 기어나 베어링 등의 기어트레인에서의 동력 손실을 줄이는 설계가 필요하다.

본 논문에서는 기어의 물림에 의한 동력손실, 기어의 쳐닝 등에 의한 회전손실 및 베어링, 싱크로나이저 등의 동력손실을 계산하는 최신의 방법을 소개하였다. 전반적인 내용을 요약하고 결과를 설명하면 다음과 같다.

1) 외접 기어트레인(Parallel-Axis Geartrain)의 동력 손실을 계산하는 최신의 방법
- 기어 접촉 및 마찰계수 해석적 모델 고려
- 기어 회전손실 모델 적용
- 베어링 동력손실 모델 적용
2) 변속기 동력흐름(Power Flow) 해석을 통한 부품 속도 및 토크 해석
3) 감속기/수동변속기/DCT의 동력손실 및 전달효율 계산하고 시험결과와 비교
- 각 단별 평균 전달효율은 감속기에서 0.38 %p, 5속 수동변속기 모델은 약 0.1 %p, 7속 DCT 모델에서 약 0.2 %p의 최대 오차를 보인다.
- 각 단별 전반적인 그래프의 개형이나 결과 값에서 추세가 잘 일치한다.

향후 이러한 이론을 바탕으로 동력 손실의 계산 뿐만 아니라 각 부품의 효율을 최적화하는 설계가 가능할 것이다.

Nomenclature


*P and P_L* :**	power or power loss and total power loss, W
T :	torque or torque loss, Nm
ω or Δω :	relative speed, rad/s
η :	efficiency, %
μ₀ :	absolute viscosity, kg/ms
μ_k :	kinematic viscosity, m²/s
ρ :	density, kg/m³
r_o and r_r :	outside and root radius of a gear, m
b :	face width of a gear, m
Z :	number of teeth of a gear, -
d_m :	pitch diameter of a bearing, m
r_ring, l_ring :	effective radius, width of a sychro. ring, m
h_ring :	gap between synchro. ring and fric. surface, m

Subscripts


S, R :	slip, rolling
g, b, j, mi :	gear, bearing, journal, miscellaneous
m, s :	mechanical, spin

References

K. Park, M. Kang, S. H. Lee, W. Son, J. Harianto, and A. Kahraman, “Prediction of Mechanical and Spin Power Losses of Parallel-Axis Geartrain in Automobile Transmission”, KSAE Spring Conference Proceedings, p121, (2017).
G. Jung, H. Kim, and J. Kim, “Performance and Transmission Efficiency Analysis of 2-Mode Hydro Mechanical Transmission”, Transactions of KSAE, 13(1), p90-98, (2005).
C. Schlegel, A. Hosl, and S. Diel, “Detailed Loss Modeling of Vehicle Gearboxes”, Proceedings 7th Modelica Conference, p434-443, (2009).
B. Hohn, K. Michaelis, and M. Hinterstoiber, “Optimization of Gearbox Efficiency”, Goriva i Maziva(Fuels and Lubricants), 48(4), p441-480, (2009).
F. J. Joachim, J. Borner, and N. Kurz, “How to Minimizer Power Losses in Transmissions, Axles and Steering Systems”, VDI International Conference on Gears, p58-66, (2010).
D. H. Park, T. S. Seo, D. G. Lim, and H. B. Cho, “Theoretical Investigation on Automatic Transmission Efficiency”, SAE 960426, (1996).
M. Kluger, and J. J. Greenbaum, “Automatic Transmission Efficiency Characteristics and Gearbox Torque Loss Data Regression Techniques”, SAE 930907, (1993).
K. Park, J. Harianto, and A. Kahraman, “Prediction and Minimization of Mechanical Power Loss of Gear Pair via Analytical Approach”, Transactions of KSAE, 25(4), p498-507, (2017). [https://doi.org/10.7467/KSAE.2017.25.4.498]
B. Wang, Z. J. Lu, X. B. Chen, P. Wang, W. Luo, and H. Xu, “Modeling and Analysis of the Dynamic Efficiency of Manual Transmission/ Reducer”, Int. J. Automotive Technology, 16(3), p417-426, (2015). [https://doi.org/10.1007/s12239-015-0043-0]
S. Li, and A. Kahraman, “A Method to Derive Friction and Rolling Power Loss Formulae for Mixed Elastohydrodynamic Lubrication”, Journal of Advanced Mechanical Design, Systems, and Manufactureing, 5(4), p252-263, (2011). [https://doi.org/10.1299/jamdsm.5.252]
S. Seetharaman, and A. Kahraman, “Load- Independent Spin Power Losses of a Spur Gear Pair: Model Formulation”, Journal of Tribology, 131(2), p022201-11, (2009). [https://doi.org/10.1115/1.3085943]
S. Seetharaman, and A. Kahraman, “A Windage Power Loss Model for Spur Gear Pairs”, Tribology Transactions, 53(4), p473-484, (2010). [https://doi.org/10.1080/10402000903452848]
T. A. Harris, and M. N. Kotzalas, Rolling Bearing Analysis - Essential Concepts of Bearing Technology, 5th Edn., Taylor & Francis, Boca Raton, (2007).
LMS Imagine.Lab AMESim, AMESim Reference Manual, Siemens PLM Software, (2016).