슬라이딩 모드 관측기를 이용한 자율주행 자동차의 모델 기반 고장 검출 및 강건 조향 제어 알고리즘
Copyright Ⓒ 2017 KSAE
Abstract
This paper describes a model-based fault detection and robust steering control algorithm for autonomous vehicles using sliding mode observers. The proposed fault detection and robust steering control algorithm is based on a bicycle model and design of sliding mode observers. The steering input that includes a fault signal has been reconstructed based on the sliding mode observer in order to detect the fault signal component with the fault signal having been reconstructed for robust control. Use of the sliding mode observer can bring not only good fault reconstruction performance but also sound robust control performance. Moreover, it is shown that the reconstructed fault and actual fault are nearly the same shape. To evaluate the performance of the proposed algorithm, path tracking simulation studies with the model predictive control algorithm have been conducted under various driving conditions. The simulation results show that the proposed model-based fault detection and robust control algorithm indeed results in both good fault detection and sound robust control performance.
Keywords:
Bicycle model, Fault detection, Autonomous vehicle, Sliding mode observer, Fault reconstruction, Robust control키워드:
자전거모델, 고장 검출 및 분리, 자율주행 자동차, 슬라이딩 모드 관측기, 고장재건, 강건제어1. 서 론
자율주행 자동차는 운전자의 조작 없이 스스로 주행환경을 인지하고 판단된 주행목적에 맞게 제어를 수행하는 자동차이다. 통계적으로 주행 중 생명을 위협하는 치명적 사고 중 약 93 %가 운전자의 실수임을 고려하였을 때 사고예방을 위한 자율주행 기술은 필수라 할 수 있다. 또한 이동 시 운전에 대한 편의성 제공과 또 하나의 생활공간으로써 활용되기 위한 자동차 기술로써의 자율주행 기술은 우리에게 다가오고 있는 미래기술 중 하나이다. 이러한 자율주행 기술은 크게 인지, 판단, 제어 세 단계로 구분될 수 있다. 인지 단계에서는 라이다, 레이더, 초음파 센서, 관성 측정장치 등 다양한 센서들을 이용하여 주행상황을 인지한다. 판단 단계에서는 인지된 주행상황을 기반으로 어떻게 주행할 것인지를 결정하는 단계로서 판단된 주행목적을 위한 요구 가속도 및 조향각을 도출하는 단계이다. 마지막으로 제어 단계에서는 실제 차량의 가속도와 조향각을 도출된 요구 가속도과 조향각이 될 수 있도록 제어가 수행된다. 이러한 인지, 판단, 제어 단계 중 한 단계에서라도 고장이 발생하면 치명적 사고가 발생할 수 있다. 그러므로 시스템의 안전성 확보를 위한 고장신호 검출 및 고립 그리고 허용제어와 관련된 다양한 연구가 수행되고 있다.
Loureiro 등1)은 대형 자율주행 자동차의 Bondgraph-model 기반 고장진단 및 고장허용 제어를 동시에 고려하여 적용할 수 있는 알고리즘을 제안하였다. 정용환 등2)은 다양한 조합의 관측기 구조를 제안하고 이를 이용하여 조향각, 요레이트, 휠스피드 센서 그리고 조향, 스로틀, 브레이크 구동기의 고장진단 시스템을 설계하고 검증하였다. 정승환 등3)은 Electronic wedge brake 클램핑 힘 센서의 수학적 수식, 모델링, 그리고 고장안전 제어 알고리즘을 연구하고 시뮬레이션 기반 검증하였다. 그리고 Tan과 Edwards4)은 슬라이딩 모드 관측기 기반 센서의 고장 신호를 검출하고 재건하는 두 가지 새로운 방법을 제시하였으며 Yin과 Huang5)은 고장검출 및 고립을 위해 요소 분석 기반 클러스터 확인, Fuzzy positivistic C-means clustering을 이용한 차량 현가장치의 고장검출 방법을 제안하였다. 문일기 등6)은 Finite state machine(FSM)방법을 이용하여 고장 발생 시 적절한 고장대처로직을 수행하는 알고리즘을 개발하고 차량주행 시스템에 적용하였다. 또한 김영준 등7)은 전기자동차의 독립 인휠모터의 전류센서 및 위치센서의 고장검출 및 고립이 가능한 모델기반의 알고리즘을 개발하였다.
기존 연구들은 일반적으로 특정 센서의 신호를 신뢰할 수 있다는 가정 하에 다른 센서의 고장신호를 검출하거나 다양한 추정이론을 통해 대체 가능한 센서를 이용하여 고장 허용 제어를 수행하였다. 하지만 본 연구에서는 자전거 모델을 기반으로 특정 센서정보를 신뢰하되 내부에서 발생할 수 있는 고장신호를 검출하고 재건함으로써 고장 강건 조향 제어를 수행할 수 있는 알고리즘을 제안하였다. 고장검출 및 강건 제어를 위해 두 가지 슬라이딩 모드 관측기를 적용하였으며 다음과 같다. 첫 번째 관측기는 강건 조향 제어에 의해 입력된 조향각을 재건하고, 두 번째 관측기는 내부에서 발생된 고장신호를 재건한다. 재건된 내부 고장신호를 이용하여 발생된 고장신호를 상쇄시키고 고장신호가 상쇄된 정상 조향신호를 제어입력으로 인가한다. 재건된 조향각은 발생할 수 있는 불확실성 정보를 이용하여 고장검출을 위한 영역을 만들고, 이를 기반으로 고장을 검출한다. 합리적인 성능평가를 위해 Matlab/Simulink 환경에서 시뮬레이션 기반 관측정보의 잡음을 고려하여 평가를 수행하였으며 평가결과 다양한 신호 및 주행조건에 대해 합리적인 고장신호와 조향각 재건 그리고 강건 제어 성능을 보여주었다. 본 논문의 나머지는 다음과 같이 구성되었다.
2장에서는 고장 검출 및 강건 조향 제어 알고리즘에 대해 기술하고, 3장에서는 시뮬레이션 기반 성능평가에 대해 기술한다. 마지막 4장에서는 본 연구의 향후계획과 함께 결론에 대해 기술한다.
2. 고장 검출 및 강건 조향 제어 알고리즘
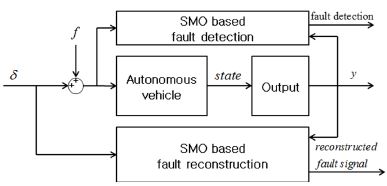
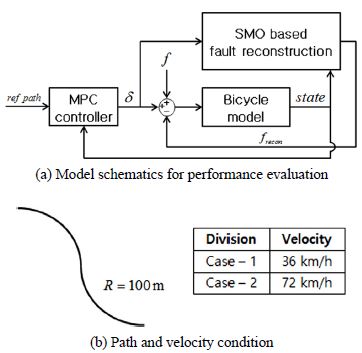
본 연구에서 제안하는 고장 강건 조향 제어 알고리즘은 크게 세 가지로 구분된다. 첫 번째는 자전거 모델을 이용하여 차량의 요 변화율과 횡방향 속도 기반 조향각을 도출하여 계측된 조향각과 비교하는 것이고, 두 번째는 비교된 조향각 신호를 기반으로 내부에서 발생된 고장신호를 재건함으로써 정상신호를 도출하는 것이다. 마지막 세 번째는 재건된 고장신호를 이용하여 정상신호를 도출하는 알고리즘이다. Fig. 1은 개발된 고장 검출 및 분리 알고리즘의 모델 개략도이다.
Fig. 1의 SMO based fault detection 블럭에서는 조향각 신호의 고장을 검출하고, SMO based fault reconstruction 블럭은 고장신호(f)를 재건한다. 다음 절에서는 슬라이딩 모드 관측기 기반 조향각 신호의 고장 검출에 대해 기술한다.
2.1 조향각 신호 고장 검출
조향각 신호의 고장을 검출하기 위해 요 변화율과 횡방향 속도를 상태변수로 갖는 자전거 모델을 이용하였으며 아래처럼 상태공간 방정식으로 표현된다.
| (1) |
| (2) |
where,
x : state vector ()
A : system matrix
B : input matrix
δ : steering angle
y : output
C : output matrix
슬라이딩 모드 관측기에 적용하기 위해 정의된 식 (1)과 (2)를 선형 좌표변환 행렬(Tc)을 이용하여 다음과 같이 변환할 수 있다.
| (3) |
| (4) |
where,
xc : transformed state vector
Tc : transformation matrix (Tc=[nullspace(C) C]T )
관측기 수식은 아래와 같이 정의되었으며 행렬 G 는 자전거 모델의 Bc 와 같도록 정의되었다.
| (5) |
where,
G=Bc
v: discontinuous injection term
슬라이딩 모드 관측기를 이용하여 차량의 조향신호 입력을 재건하기 위해 식 (3)의 Bc를 0으로 간주하여 Error dynamics를 도출하였다.
| (6) |
where,
앞서 정의된 선형 좌표변환 행렬을 이용하여 도출된 Error dynamics는 다음과 같이 상태변수(e1)와 출력(ey)에 관련된 수식으로 구분된다.
| (7) |
| (8) |
where, A11,A12,A21,A22: elements of the matrix Ac
출력오차와 상태변수 오차의 수렴 안정성을 확보하기 위해 먼저 출력오차 ey를 유한 시간 내 정의된 슬라이딩 서피스 S={ey:ey=0}로 수렴시킬 수 있게 Eta-reachability condition 기반 ρ의 범위를 도출하고 Injection term(v)을 아래와 같이 계산될 수 있도록 하였다.8)
| (9) |
유한시간 내 ey는 0으로 수렴하기 때문에 식 (8)의 veq을 도출하면 아래와 같다.
| (10) |
where, veq : equivalent injection term
도출된 veq를 식 (7)에 대입하면 아래와 같은 수식을 도출할 수 있다.
| (11) |
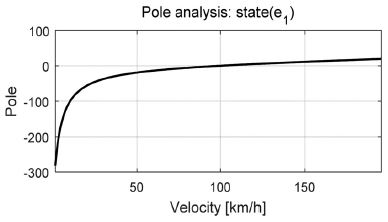
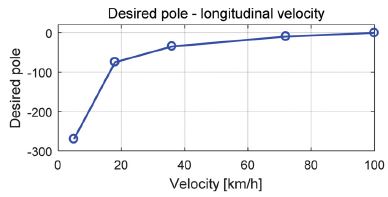
상태변수에 대한 오차 e1을 0으로 수렴시키기 위해서는 수식 내 pole 이 항상 음의 값을 가져야한다. 하지만 차량의 물성치와 속도에 따라 달라지기 때문에 속도에 따른 부호 확인이 필요하며 물성치는 실제 차량의 값이 적용되었다. Fig. 2는 차량의 속도에 따른 Pole을 나타낸다.
차량의 속도가 약 0 km/h ~ 98 km/h 구간에서 Pole의 모든 값이 음수이기 때문에 대상 차량은 상태변수에 대한 오차 수렴 안정성이 약 100 km/h 내에서 확보될 수 있음을 확인할 수 있었다. 앞서 정의된 행렬 G 는 변환된 자전거모델의 행렬 Bc와 같기 때문에 관측기의 Equivalent injection term(veq)은 차량의 조향각 신호를 의미한다. 하지만 계측된 조향각 신호와의 비교를 위해서는 자전거 모델과 실제 차량과의 오차와 계측된 신호들의 잡음으로 인해 다음과 같이 불확실성(vun)을 고려해야한다.
| (12) |
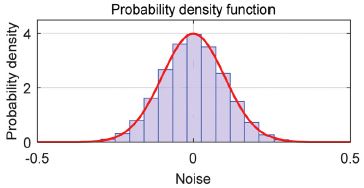
정의된 불확실성은 평균 0, 표준편차 0.005인 정규분포로 가정하였으며 향후 불확실성에 대한 수학적 분석 및 실험 데이터 분석을 통해 정확도를 높일 계획이다. 아래 수식은 재건된 조향각 신호를 이용한 고장검출 조건을 보여준다.
| (13) |
| (14) |
where,
δrecon,max : maximum value of δrecon
δrecon,min : maximum value of δrecon
조향각의 최대 및 최소값은 정의된 불확실성의 3σv 값을 이용하여 도출하였으며 아래와 같다.
| (15) |
| (16) |
횡방향 속도와 요 변화율을 이용한 조향각 신호의 재건 성능에 따른 고장검출은 다음 장의 알고리즘 성능평가 시 조향입력 신호 재건을 통한 고장신호 검출 수행을 통해 평가되었다. 식 (15)와 (16)에서 정의된 고장검출을 위한 최대값 및 최소값을 이용하여 계측된 조향각 신호가 최대/최소 영역 내 있으면 정상, 영역 밖에 있으면 고장으로 진단되도록 알고리즘을 구성하였다. 다음 절은 슬라이딩 모드 관측기 기반 조향각 고장신호 재건 및 분리 알고리즘에 대해 기술한다.
2.2 고장신호 재건 알고리즘
조향각 고장신호를 재건하기 위해 아래와 같이 고장신호를 포함하는 자전거 모델과 슬라이딩 모드 관측기 수식을 정의하였다.9)
| (17) |
| (18) |
where, D : fault distribution matrix (D=Bc)
위 수식을 이용하여 아래와 같이 고장신호와 관측기의 Injection term(veq)으로 구성된 Error dynamics를 도출할 수 있다.
| (19) |
Error dynamics의 구분된 출력오차에 대한 수렴성능을 확보하기 위해 2.1절에서 정의된 Eta-reachability condition을 이용하여 Injection term을 정의하였다. 그리고 상태변수에 대한 수렴성능 확보를 위해 설계변수 L 을 이용하여 Gr을 아래와 같이 정의하였다.
| (20) |
식 (2)에서 정의된 Gr을 이용하여 도출된 상태변수 오차에 대한 수식은 아래와 같다.
| (21) |
차량의 종방향 속도에 따라 변하는 pole의 부호가 항상 음의 값이 되도록 설계변수 L을 정의함으로써 수렴안정성이 확보될 수 있다. 이를 기반으로 오차 e를 0으로 간주하면 고장신호 f는 아래와 같이 Pseudo inverse를 이용하여 재건될 수 있다.
| (22) |
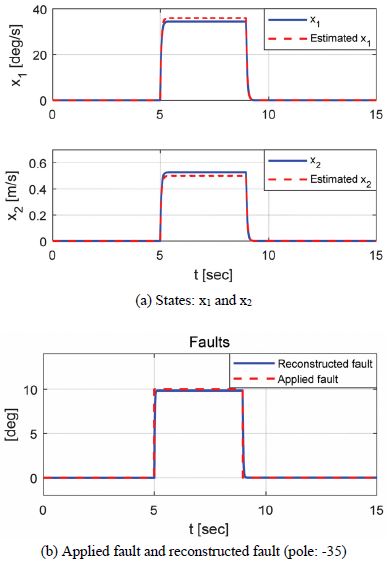
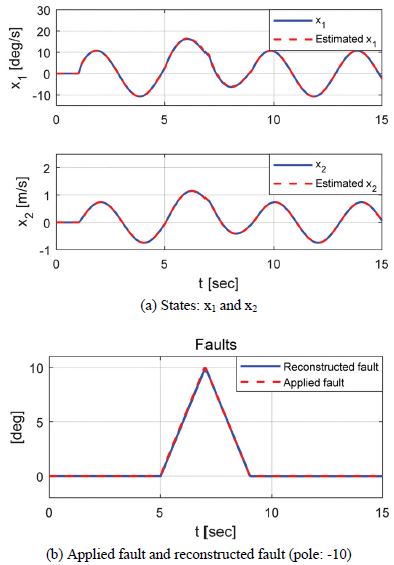
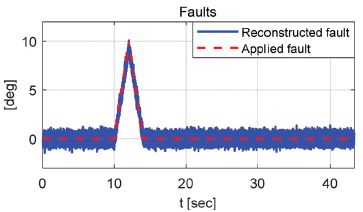
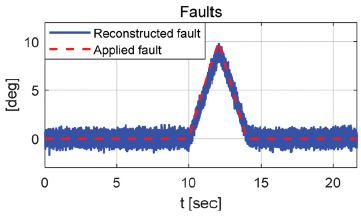
Fig. 3과 4는 자전거 모델 기반 임의의 고장신호에 대해 제안된 알고리즘을 이용하여 재건된 고장신호를 다양한 속도와 조향입력 조건에 따라 비교한 결과를 보여준다.
Fig. 3에서 36 km/h, 조향이 없고 사각파형의고장신호가 인가되었을 때 변화율이 큰 고장신호의 시작점에서는 정확하게 사각파형을 재건하지는 못했지만 Pole의 값이 -35의 값일 때 합리적인 고장신호의 재건성능을 확인할 수 있었다.
고장신호의 재건 결과를 보면 설계변수로써 정의된 Desired pole의 값이 속도에 따라 적절한 값이 정의되어야 정확한 고장신호의 재건이 가능함을 확인할 수 있다. 이러한 현상은 차량의 속도에 따라 조향에 따른 반응성이 달라지기 때문이다. 하지만 조향입력의 유무 조건에도 강건한 재건성능을 확인할 수 있었다. 그러므로 다음 절에서는 속도에 따른 Desired pole의 최적 값 도출과 함께 고장 강건 조향제어 알고리즘에 대해 기술한다.
2.3 고장 강건 조향 제어 알고리즘
재건된 고장신호의 정확도는 차량의 속도에 따라 변하기 때문에 속도에 따른 L 값이 정의되어야 한다. 차량의 관성과 전/후장 값에 따라 달라질 수 있지만 본 연구에서는 차량의 고정된 전/후장 값이 적용되어 속도만 변한다고 가정하였다. 정의된 가정을 통해 대상 차량의 속도와 최적 L값에 따른 Desired pole을 시뮬레이션 기반 경험적으로 도출함으로써 고장 강건 조향 제어 알고리즘을 설계하기 위한 규칙을 도출하였다. Fig. 5는 종방향 속도에 따라 도출된 최적 Desired pole의 값 보여준다.
Fig. 5에서 볼 수 있듯이 Desired pole은 차량의 속도가 증가할수록 0에 가까워지는 것을 확인할 수 있다. 이는 변환된 행렬(Ac)에 의해 구성되는 식 (7)과 (8)은 차량의 종방향 속도가 포함되어 있고, 오차를 0으로 수렴시키기 위한 veq의 결정에 영향을 준다. 그러므로 veq를 이용하여 합리적으로 고장신호를 재건하기 위해서는 Time-varying parameter인 속도에 따른 최적 Desired pole의 도출이 필요하다.
고장신호에 대한 강건한 조향각 입력 신호를 도출하기 위해 아래와 같이 재건된 고장신호를 이용하여 정상신호를 도출하였다.
| (23) |
재건된 고장신호는 δrecon≈f이기 때문에 Fig. 1과 같이 고장신호가 발생하더라도 δc,normal≈δ이 되어 계산된 정상신호로 제어가 가능하다. 다음 장에서는 제안된 강건 제어 알고리즘의 성능평가 결과를 보여준다.
3. 시뮬레이션 기반 성능평가
본 연구에서는 제안된 고장 강건 알고리즘의 합리적 성능평가를 위해 차량동역학 모델 기반 단순화된 자전거 모델을 이용하였으며 다양한 속도 조건 하에 곡선주행 시나리오가 적용되었다. 그리고 관측 잡음의 고장신호 재건 및 강건 제어 성능에 대한 영향도를 평가하기 위해 임의의 Gaussian noise를 인가함으로써 성능평가를 수행하였다. Fig. 6은 성능평가를 위해 사용된 모델개략도와 곡선로 그리고 속도 조건을 보여준다.
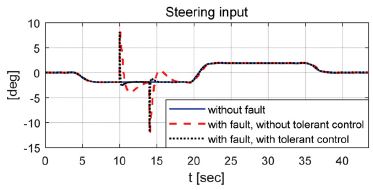
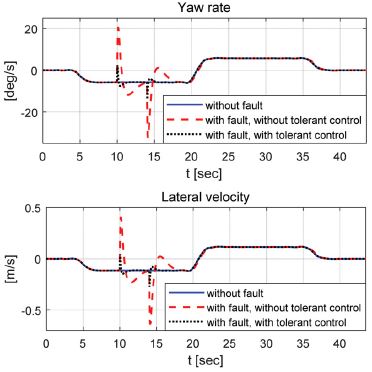
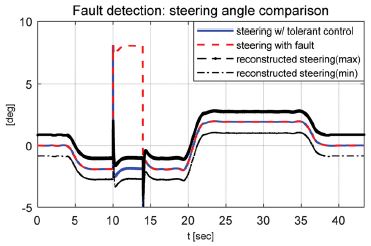
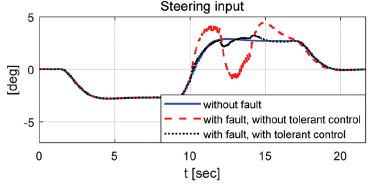
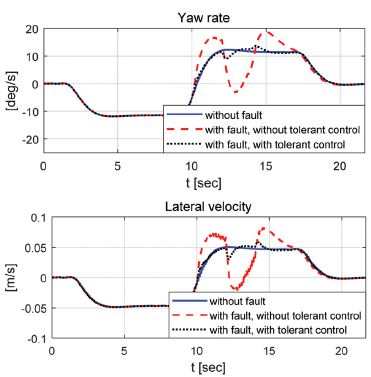
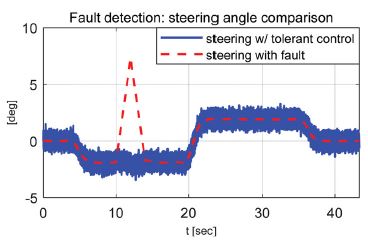
성능평가는 36 km/h와 72 km/h 속도조건에서 수행되었으며 MPC(Model predictive control) 제어 알고리즘을 이용하여 회전반경 90 m인 곡선경로를 추종하도록 모델을 구성하였다. 강건 제어 알고리즘의 성능평가를 위해 경로추종 중 임의의 고장신호를 인가하여 강건 제어가 적용된 경우와 적용되지 않은 경우 그리고 고장신호가 인가되지 않은 경우에 대해 조향각과 동적거동 그리고 주행경로를 비교 / 분석 하였다. 적용된 임의의 고장신호는 Fig. 3과 Fig. 4에서 적용된 사각파와 삼각파가 적용되었으며 10초 ~ 14초 사이에 인가되었다. Fig. 7 ~ 14는 성능평가 결과를 보여준다. Case -1의 경우 36 km/h 조건에서 사각 고장신호가 인가되었으며 강건 제어 결과 내부에서 발생된 고장신호의 합리적 재건에 따라 고장신호가 없을 때와 같은 조향제어 성능이 확보되었음을 확인할 수 있었다.
Case - 1) Velocity - 36 km/h, square fault
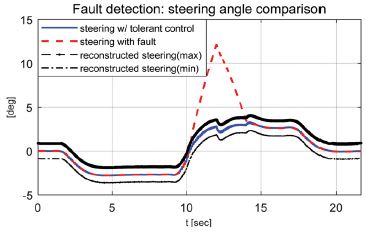
강건 제어가 적용되어 재건된 조향각과 불확실성을 고려해 도출된 영역을 이용하여 고장신호가 포함된 조향각 신호가 확실히 구분될 수 있음을 확인할 수 있었다. 그리고 고장신호가 상쇄되어 정상상태의 제어성능을 확보할 수 있었다.
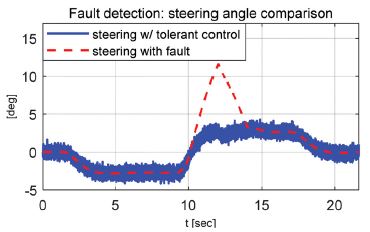
Case - 2) Velocity - 72 km/h, triangular fault
고장신호 재건을 위해 사용된 관측값에 임의의 잡음을 적용하여 제어 성능을 확인하였다. Case - 3는 잡음 조건 하의 성능평가 결과를 나타낸다.
Case - 3) Velocity - 36 and 72 km/h, triangular fault, with Gaussian noise
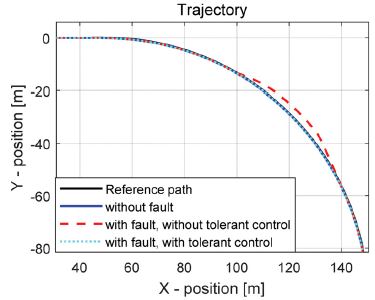
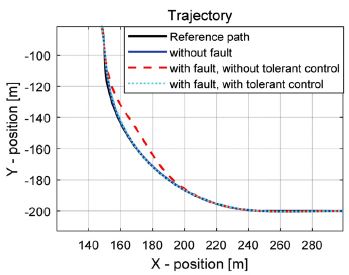
강건 제어 결과 정상상태의 조향입력에 비해 고장신호가 완벽히 재건되지 못하기 때문에 작은 오차가 발생하는 것을 확인할 수 있었다. 하지만 합리적인 제어성능이 확보되어 경로추종의 오차가 고장신호가 없는 정상상태와 크게 다르지 않다는 것을 경로추종 오차의 실효값 분석을 통해 확인할 수 있었다. 주행경로 분석 결과를 보면 강건 제어가 적용되지 않은 경우 경로추종 제어기에 의해 고장신호가 없어진 이후 경로를 합리적으로 추종하였지만 고장신호가 인가된 구간에서는 경로를 이탈하는 것을 확인할 수 있었다. 그리고 관측값에 평균 0, 표준편차 0.0999의 Gaussian noise가 적용된 경우에도 합리적인 고장신호의 재건 및 강건 조향제어 성능을 확인하였다. 다음 장은 본 연구의 향후계획을 포함하는 결론에 대해 기술한다.
4. 결 론
본 연구에서는 슬라이딩 모드 관측기를 이용하여 자율주행 자동차를 위한 자전거 모델 기반 고장 검출 및 강건 조향 제어 알고리즘을 제안하였다. 차량의 요 변화율과 횡방향 속도를 계측 가능하다고 가정하였으며 이를 기반으로 조향각에 대한 내부 고장신호를 재건하였다. 하지만 현실적으로 횡방향 속도의 계측 및 추정에 따른 적용은 어렵기 때문에 향후 횡방향 속도를 포함하지 않는 기구학 모델을 이용한 알고리즘의 개발을 계획하고 있다. 재건된 내부 고장신호를 이용하여 정상 조향신호를 도출하여 강건 제어 알고리즘을 구성하였고, 횡방향 속도와 요 변화율을 이용하여 조향입력 신호를 재건하고 고장신호를 포함하는 조향각 신호와 비교함으로써 고장 검출을 수행할 수 있었다. 합리적인 성능평가를 위해 다양한 속도조건과 고장신호에 대해 곡선주행 시나리오가 적용되었으며 모든 조건에 대해 좋은 강건 제어 성능이 확보될 수 있음을 확인하였다. 하지만 본 연구에서 제안하는 고장검출 및 강건 제어 알고리즘은 차량의 횡방향 속도와 요 변화율의 정보를 신뢰하고 있고, 오직 조향각의 내부 고장신호에 대한 강건 제어를 수행하고 있다는 점 그리고 시속 100 km/h 이상에서는 조향각 신호 재건을 위한 관측기의 수렴 성능이 확보될 수 없다는 한계점들이 있다. 그러므로 향후 차량의 속도 전 구간에서 Pole이 음의 값이 될 수 있도록 관측기의 좌표변환 행렬(Tc)을 설계하고, 고장신호의 재건성능을 확보할 계획이다. 또한 개별 센서의 고장신호를 검출 및 재건할 수 있도록 알고리즘의 고도화를 계획하고 있다. 또한 잡음이 존재하는 경우 고장신호의 재건 및 고립 시 고주파영역의 잡음에 의한 제어성능 저하를 방지할 수 있도록 필터링 기법을 적용할 것을 고려하고 있다. 그럼에도 불구하고 제안된 알고리즘은 조향각 내부 고장신호에 대한 좋은 강건 제어성능을 보여주었기 때문에 향후 자율주행 자동차의 고장안전 시스템으로 적용될 수 있을 것이라 기대한다.
Nomenclature
| : | yaw rate, rad/s |
| vy : | lateral velocity, m/s |
| f : | fault signal, rad |
| δrecon : | reconstructed steering angle, rad |
| vvn : | steering uncertainty, rad |
| δc,normal : | computed normal steering angle, rad |
| e1 : | state error |
| ey : | output error |
| Tc : | transformation matrix |
| v : | discontinuous injection |
| A : | system matrix |
| B : | input matrix |
Subscripts
| y : | lateral direction |
| recon : | reconstructed |
| un : | uncertainty |
| c,normal : | computed normal |
| c : | transformed |
| eq : | equivalent |
Acknowledgments
A part of this paper was presented at the KSAE 2017 Spring Conference
본 연구는 정부(미래창조과학부)의 재원(NRF-2016 R1E1A1A01943543)으로 한국연구재단의 지원을 받아 수행된 사업임.
References
-
R. Loureiro, S. Benmoussa, Y. Touati, R. Merzouki, and B. Bouamama, “Integration of Fault Diagnosis and Fault-Tolerant Control for Health Monitoring of a Class of MIMO Intelligent Autonomous Vehicles”, IEEE Transactions on Vehicular Technology, Vol.63(No.1), p30-39, (2014).
[https://doi.org/10.1109/tvt.2013.2274289]

-
Y. Jeong, K. Kim, B. Kim, J. Yoon, H. Chong, B. Ko, and K. Yi, “Vehicle Sensor and Actuator Fault Detection Algorithm for Automated Vehicles”, IEEE Intelligent Vehicles Symposium (IV), p927-932, (2015).
[https://doi.org/10.1109/ivs.2015.7225803]

-
S. Chung, and H. Lee, “A study on the Clamping Force Estimation and Failsafe Control Algorithm Design of the Electronic Wedge Brake System”, Transactions of KSAE, Vol.24(No.1), p16-23, (2016).
[https://doi.org/10.7467/ksae.2016.24.1.016]

-
C. Tan, and C. Edwards, “Sliding Mode Observer for Detection and Reconstruction of Sensor Faults”, Automatica, Vol.38, p1815-1821, (2002).
[https://doi.org/10.1016/s0005-1098(02)00098-5]

-
S. Yin, and Z. Huang, “Performance Monitoring for Vehicle Suspension System via Fuzzy Positivistic C-Means Clustering Based on Accelerometer Measurements”, IEEE/ASME Transactions On Mechatronics, Vol.20(Issue 5), p2613-2620, (2015).
[https://doi.org/10.1109/tmech.2014.2358674]

- I. Moon, J. Ahn, and K. Yi, “A Fault Diagnosis and Fault Handling Algorithm for a Vehicle Cruise Control System”, Transactions of KSAE, Vol.12(No.1), p216-221, (2004).
- Y. Kim, N. Jeon, and H. Lee, “Model based Fault Detection and Isolation for Driving Motors of a Ground Vehicle”, Sensors & Transducers, Vol. 199(Issue 4), p67-72, (2016).
-
Y. Shtessel, C. Edwards, L. Fridman, and A. Levant, Sliding Mode Control and Observation, Springer, New York, (2014).
[https://doi.org/10.1007/978-0-8176-4893-0]

- K. Oh, and K. Yi, “Model-based Fault Detection Algorithm for Steering System in Autonomous Vehicle using Sliding Mode Observer”, KSAE Spring Conference Proceedings, p874-875, (2017).