현가장치의 예견 제어를 위한 초음파 센서 모듈
Copyright Ⓒ 2017 KSAE
Abstract
Lidars and stereo cameras are used as preview sensors for advanced suspension systems. However, there are circumstances where these sensors are not able to recognize the road surface well due to physical or algorithmic issues. Sensor modules with a high-performance processor and high-capacity memory are very expensive, making mass production very challenging. To overcome this challenge, this paper introduces ultrasonic sensors as a cost-efficient tool to build sensor modules. Aside from being cost-efficient, the ultrasonic sensor module has a relatively simple algorithm that makes it possible to retrieve road surface data with micro controller units. This paper also suggests methods to obtain real-time road surface information from the environment with high noise level. To test the suggested methods, simulations and road tests were performed.
Keywords:
Preview control sensor, Ultrasonic sensor, Road surface estimation, Road surface mapping, Time-of-flight키워드:
예견 제어용 센서, 초음파 센서, 노면 추정, 노면 매핑, 비행시간1. 서 론
승차감과 핸들링 성능은 차량을 평가할 때 매우 중요한 부분이다. 그러나 이 둘은 현가장치 시스템 세팅에서 서로 상충 관계에 있다. 따라서 이 두 성능을 모두 개선하기 위한 다양한 연구가 이루어져왔으며, 이와 함께 현가장치 시스템이 개선되어왔다.1,2) 과거에는 스프링과 댐퍼의 고정된 특성으로만 휠에서 차체로의 외력 변화의 전달을 억제하였다. 그러나 최근에는 현가장치 내의 댐퍼 감쇠 계수를 바꾸거나 모터의 힘을 차량 상태에 따라 능동적으로 제어함으로써 차체의 자세를 보다 안정시킬 수 있고 진동을 억제 시킬 수 있다.3,4) 기존의 수동 현가장치 시스템과는 달리, 이러한 시스템은 능동적으로 혹은 반 능동적으로 외란을 억제하기 때문에 능동 또는 반 능동 현가장치라고 한다.
그러나 새로운 현가장치 시스템의 개발에도 불구하고 다른 한계가 있었다. 위의 새로운 현가장치 시스템은 모든 도로 조건에 대하여 최적화 될 수 없기 때문에 평균적인 도로 표면에서만 잘 작동하도록 제어기가 세팅된다. 즉, 미래의 다가올 노면을 미리 알 수 없기 때문에 현가장치 제어에 제약이 생긴다. 또한, 현가장치 시스템의 느린 작동 속도, 즉 제한된 시스템 제어 대역폭으로 인해 실시간으로 대응하기가 어렵다. 이러한 하드웨어적 제약을 극복하기 위해 다가올 노면을 미리보기위한 예견 센서가 적용되기 시작했다.5-7)
예견 센서는 가까운 미래에 다가올 도로 표면 정보를 전송하여 현가장치 시스템을 적절히 제어하는 데 사용된다. 현가장치는 이를 통해 다양한 노면 조건에서 성능을 극대화 시킬 수 있다. 지금까지는 스테레오 카메라와 라이다가 예견 센서로 널리 사용되었다.8,9) 두 센서 모두 측정을 위해 빛을 사용하므로 상대적으로 장거리를 측정 할 수 있다. 특히, 스테레오 카메라는 고해상도 이미지에서 다양한 정보를 얻을 수 있는 수동 센서 중 하나로, 샘플링 속도는 비교적 낮다. 두 개 이상의 영상을 합성함으로써 노면의 높이 정보를 고정밀로 얻을 수 있다. 반면 라이다는 능동 센서 중 하나이며 높은 샘플링 속도로 노면 정보를 신속하게 수신 할 수 있다. 또한 지나갈 노면에 레이저를 직접 조사함으로써 제어에 효율적인 노면 측정이 가능하다.
그러나 상기 두 개의 센서는 일반적인 차량에 적용하기에는 너무 고가이다. 또한 센서에서 출력으로 나온 대용량의 데이터를 처리하기 위해서는 고성능의 프로세서와 대용량의 메모리를 사용해야한다. 그리고 정보원으로 빛을 이용하기 때문에, 반사된 빛이 비정상적인 상황에서는 센서가 오작동 할 가능성이 높다. 예를 들어, 카메라에 입사되는 빛의 양이 매우 많거나 낮으면 주변 환경을 인식하는 것이 거의 불가능하다. 특히 라이다의 경우 레이저 시스템을 차량 외부에 노출시켜야만 제대로 된 측정이 가능하며, 측정 대상물의 반사량에 따라 오차가 발생할 수 있다. 그리고 카메라처럼 눈, 비, 먼지와 같은 작은 장애물에도 직접적인 영향을 받는다.
이러한 한계점을 낮은 비용으로 해결하기 위해, 본 논문에서는 초음파 센서를 예견 센서로 제안한다. 저렴한 가격과 낮은 계산량으로 다양한 분야에서 초음파 센서가 사용되고 있다. 특히 로봇이나 차량 분야에서 비행시간(Time of flight)을 사용하여 주변 환경을 인지하는데 사용된다.10-12) 특히, 차량 분야에서 주차 보조시스템이나 저속에서의 적응형 크루즈 컨트롤(Adaptive cruise control)을 위해 사용되고 있다.17) 이러한 초음파 센서를 지면에 수직으로 송수신함으로 차량과 노면의 거리를 측정할 수 있다. 즉, 이동체가 지나갈 노면과 이동체 사이의 거리를 연속적으로 측정 할 수 있고, 능동 또는 반 능동 현가장치의 제어기에 예견 정보를 제공함으로써, 로봇이나 차량의 흔들림을 억제 할 수 있다.
그러나 초음파는 주변 잡음에 영향을 받기 쉽고 측정 대상으로부터의 거리가 증가함에 따라서 신호의 신뢰성이 감소한다.13) 또한 다른 센서보다 시야각이 넓기 때문에 주변 환경의 세밀한 매핑(Mapping)이 불가능하다. 본 논문에서는 이러한 단점을 극복하기 위해 송신기와 수신기를 따로 두고, 수신기의 수를 늘릴 뿐만 아니라, 초음파 센서 모듈을 휠 축과 비슷한 높이에 장착한다.12) 또한, 저성능 마이크로 컨트롤러(Micro control unit)에서도 처리 가능한 측정치 보정 및 간단한 신호 처리가 수행되어 전술한 신호의 결함을 보완한다. 제안된 방법을 검증하기 위해서 노면 매핑 시뮬레이션뿐만 아니라, 개발된 센서 모듈을 실차에 장착하여 노면 높이 추정 실험을 수행하였다.
본 논문은 2장에서 노면 높이를 측정하기 위한 센서 모듈의 하드웨어 구성 및 비행시간 결정에 대해 설명하고, 3장에서 노면의 높이를 추정하기 위한 알고리즘을 제시한다. 알고리즘은 도로면 높이 추정을 위한 모델링 및 길이 방향 변위 보상을 포함한다. 또한 4장은 측정한 위치에 대해 종방향 변위를 추정하고, 5장과 6장은 실험과 결론을 기술한다.
2. 센서 모듈 구성
2.1 하드웨어 설명 및 초음파 인식
초음파 센서 모듈은 하나의 송신기와 하나 이상의 수신기로 구성된다. 또한 CAN 버스가 장착 된 저가의 16 MHz MCU를 사용하여 센서의 신호를 처리하고, 현가장치 컨트롤러에 도로 표면 정보를 전달한다. 여기서 현가장치 제어기는 이 노면 높이를 목표치와 비교하고, 높이 방향의 가속도와 저크를 함께 고려하여 제어하게 된다.
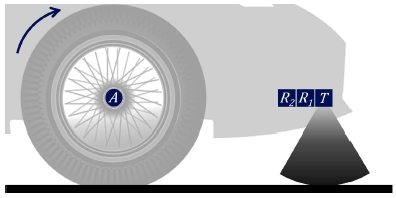
예견 센서 모듈은 Fig. 1처럼 차량의 전방 범퍼와 타이어 사이에 센서를 장착하여 다가오는 노면의 높이를 측정한다. Fig. 1에서 A는 바퀴 축을 나타내고 T와 R은 센서 모듈의 송신기와 수신기를 나타낸다. 송신기에서 초음파는 부채꼴 형태로 방사되기 때문에 모듈이 바퀴 축의 높이와 비슷한 높이에 설치 될 때 초음파가 도로 표면에 처음 닿는 모양은 타이어가 지나가는 노면에 접촉하는 형태와 비슷하게 된다. 차량의 휠과 타이어는 고주파 레벨의 울퉁불퉁 한 노면에 대해서 필터 효과를 가지므로, 센서 모듈의 높이를 Fig. 1에 표시 된 바와 같이 휠 축과 비슷한 높이로 설치하면 휠 축이 통과하는 노면의 높이가 보다 정확하고 효과적으로 측정될 수 있다.
초음파 송신기는 MCU로부터 송신 신호를 명령받으면 압전 소자를 진동시켜 초음파를 발생시킨다. 발생된 파장이 목표물에서 반사되면 초음파 수신기는 MCU에 응답 신호를 보내게 된다. MCU는 초음파를 전달 한 시각과 응답이 수신 된 시각 간의 차이인 비행시간을 이용하여 노면에서부터 센서 모듈까지의 거리를 얻을 수 있게 된다. 즉, 아래의 비행시간 이용 거리 측정식을 사용하여 거리를 계산한다.
| (1) |
여기서 d는 음파가 이동 한 거리, v는 그 당시 환경에서의 음파의 속도이며, ttof는 비행시간이다.
2.2 초음파 인식 방법
비행시간을 측정하려면 대상물로부터 반사된 초음파를 인식해야한다. 이 인식 방법에는 엔빌로프(Envelope) 방법, 상호 상관(Cross correlation) 방법, 모델 기반 방법, 임계값(Threshold) 방법을 포함하는 방법들이 있다.14,15) 임계값 방법을 제외한 모든 방법은 초음파의 주파수보다 훨씬 높은 샘플링 속도로 원시 신호(Raw Signal)를 측정해야하며 많은 양의 샘플링된 데이터를 처리해야하기 때문에 큰 메모리와 고성능 프로세서도 요구된다. 따라서 하드웨어로 쉽게 구성할 수 있고 저렴한 MCU에서 사용가능하며 외부 노이즈에 강인한 임계값 인식 방법을 사용하기로 한다.
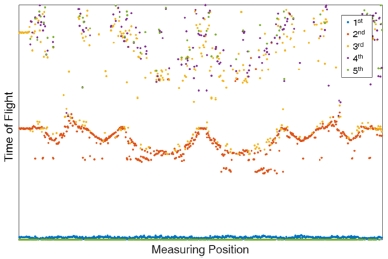
이 때 임계값은 특정 값으로 설정되어야한다. 임계값이 낮아지면, Fig. 2에 도시 된 바와 같이 노면 및 차체로부터의 다회 반사 된 신호가 수신 될 수 있다. Fig. 2는 관측 위치를 변화시켜가며 한번 초음파 송신 시 수신되는 신호들을 나타낸 것이며, 노면 정보뿐만 아니라 주변 환경으로부터 많은 잡음이 초음파 수신기로부터 수신되고 있고, 노면 정보를 포함하여 최대 5회 수신된다. 따라서 송신기에서 수신기로 바로 전달되는 신호 하나, 그리고 가장 가까운 노면에서 반사된 신호 하나, 총 2개의 신호가 수신되도록 수신기의 임계값을 조절한다.
3. 노면 높이 추정
3.1 노면 높이 추정 알고리즘 선정
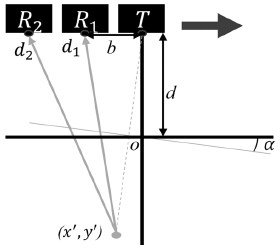
모델링의 간소화를 위해 하나의 송신기와 2개의 수신기가 있고, 도로 표면이 평평하다고 가정한다. 즉 Fig. 3에 도시된 바와 같이, 노면은 경사가 있는 평탄한 도로와 노면 위를 움직이는 센서와의 거리에 의해서 정의 될 수 있다. d는 센서 모듈에서부터 도로 표면까지의 거리이고, α는 평평한 도로 표면의 기울기이다. 그리고 b는 센서 사이의 거리이고 d보다 10배 이상 작다. 또한, d1 및 d2는 송신된 신호가 수신기 R1 및 R2에 도달 할 때까지 초음파가 이동한 거리이다.
가장 가까운 목표물이 검출되는 초음파 센서의 특성을 고려하면, Fig. 3에서 거리 d와 기울기 α에 따라 (x′,y′)=(-dsin2α,-dcos2α)에서 초음파가 송신된 것과 같다고 할 수 있다. 따라서 초음파의 이동거리 d1 및 d2는 다음과 같이 표현될 수 있다.
| (2) |
초음파 수신기로부터 얻게 되는 d1 및 d2를 이용하여, 노면으로부터 센서 모듈까지의 거리 d는 (2)로부터 아래의 식으로 얻어 질 수 있다.
| (3) |
여기서 dm은 모델 기반의 센서와 노면 사이의 거리이다. 이 식은 복잡한 제곱근과 제곱근을 가지므로 거리 dm을 얻으려면 많은 계산량이 필요하다. 그러므로 초음파 수신기들의 출력이 비슷하다는 점과 센서간의 거리는 매우 짧다는 점을 이용하여 d1 ≈ d2와 b ≈ 0로 (3)을 근사시키면 다음과 같은 간단한 식을 얻을 수 있다.
| (4) |
여기서 da는 가정이 포함된 모델의 노면으로부터의 거리이다.
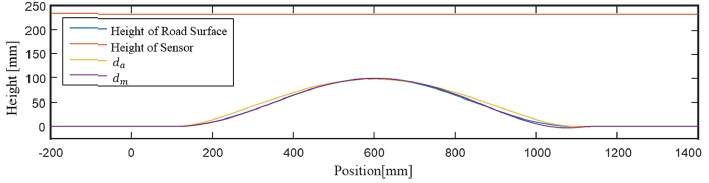
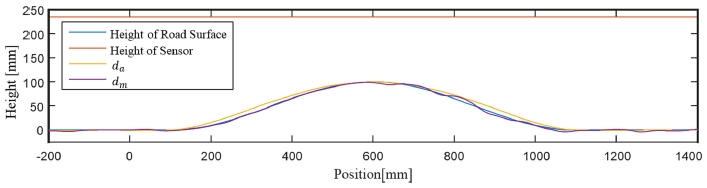
위의 (3)과 (4)를 비교하기 위해, 100 mm 높이의 범프 표면에서의 추정 성능을 시뮬레이션으로 평가하였다. 주변 잡음이 없는 환경에서 시뮬레이션한 결과는 Table 1과 Fig. 4에 나타내었다.
표에서 RMSE는 평균 제곱근 오차를 의미한다.
Fig. 4에서 dm의 경우, 범프를 통과 할 때까지 오차가 매우 작으며 범프의 끝에서 가정의 왜곡으로 인해 약간의 오차가 나타난다. 한편, da의 경우, 노면이 평탄하지 않은 부분, 즉 가정이 어긋나는 부분에서 오차가 커지는 것을 확인할 수 있다.
표에 나타난 것처럼 da의의 성능은 dm의 성능보다 약간 낮다. 그러나 da의 오차는 범프의 높이에 비해 4 % 내외이며, dm식의 제곱 및 제곱근을 제거하여 계산의 복잡성을 크게 줄일 수 있다. 또한, da는 각각의 수신기에 대해 독립적으로 사용될 수 있다. 따라서 수신기의 수가 증가하면 노면의 정보량이 증가하므로 주변 잡음이 많은 차량 환경에서도 보다 강인한 도로 노면 추정이 가능해진다.
이 점을 확인하기 위해 위의 시뮬레이션을 수신 정보에 대해 5 %의 무작위 잡음을 추가하여 반복하였으며 그 결과를 Table 2와 Fig. 5에 나타내었다.
적절한 저역 통과 필터를 사용하면 da는 주변 잡음이 없을 때와 거의 비슷하게 추정되지만 dm은 부드러운 노면 높이의 변화에도 추정치가 많이 흔들리는 것을 확인 할 수 있다. 주변 잡음을 10 % 이상으로 시뮬레이션하면 추정된 dm 중 많은 부분이 복소수 영역에 있음을 확인하였기 때문에 실제 차량에 적용하기 힘들다는 것을 알 수 있다. 그러므로 주변 잡음에 강인한 da를 실차의 도로 표면 높이 추정에 사용하기로 한다.
3.2 비행시간 결정 및 도로 표면의 매핑
초음파 센서 모듈이 물체로부터의 거리를 측정하도록 명령을 받으면 송신기의 압전 소자는 수 us 동안 진동 진폭이 증가하다가 감소된다. 따라서 수신 신호의 강도도 점차적으로 증가하다가 감소한다.
임계 값 인식 방법을 사용하는 경우, 신호 세기가 반사파의 초기 도달로부터 임계값에 도달 할 때까지 시간 편차가 존재하게 된다. 그러나 노면과의 거리가 대략적으로 정해져있고, 검출 신호의 임계값이 특정되면, 수신 된 초음파 신호는 소정 시간 후에 인식된다. 이 사실을 바탕으로 센서 오프셋, MCU 오프셋 및 센서 장착 위치에 따른 오프셋을 고려하면 식 (1)과 식 (4)에서 다음 식 (5)가 유도된다.
| (5) |
여기서, t1은 송신 된 신호가 처음으로 첫 번째 수신기에 도달한 시간이고, to,1은 초음파가 지정된 임계값을 초과하는 시간이다. 또한, tb,1은 t1과 to,1 사이의 시간차이고, db,1은 첫 번째 수신기에 대해 거리 관련 편차이다.
위 식은 두 번째 수신기에 대해서도 식 (6)과 같은 식을 얻을 수 있고, 식 (5)과 식 (6)을 일반화하면 식 (7)과 식 (8)로 표현 할 수 있다.
| (6) |
| (7) |
| (8) |
여기서 a1,x 및 a2,x는 수신기 출력으로부터 거리를 추정하기 위한 계수이며, 각 수신기 출력에 대해 1차 선형 방정식으로 근사되므로 2개의 알려진 거리를 통해 계수를 얻을 수 있다. 이 계수를 적용하여, 센서 모듈과 노면 사이의 거리는 초음파 송신시마다 수신기의 정보를 통합함으로써 얻어 질 수 있다.
마지막으로 노면과의 거리 d는 da,1와 da,2로부터 간단한 저역 통과 필터와 가중치 함수를 적용하여 추정 할 수 있다.
4. 종방향 위치차 추정
현가장치 제어를 위한 예견 센서로서 초음파 센서 모듈을 사용하기 위해서는, 센서에 의해 측정 된 노면의 높이 정보뿐만 아니라 종방향 내에서 측정된 부분과 휠 축간의 거리를 알 필요가 있다. 이 길이는 차량이 멈춰 있을 때는 일정하지만 차량이 빨리 달릴수록 줄어들게 된다. 즉, 센서 모듈의 장착 위치, 차량의 진행 방향 및 속도에 따라 달라진다. 따라서 종방향의 위치차를 추정하는 과정은 필수 불가결하다. 상기된 내용을 기초하여 종방향 내에서 노면 높이가 추정되는 지점과 휠 축 사이의 거리에 대한 방정식은 다음과 같이 설정 될 수 있다.
| (9) |
여기서 x는 측정 지점과 휠 축 사이의 거리, vx는 차량의 종방향 속도, b1과 b2는 보정 매개 변수이다.
매개 변수 b1과 b2는 알려진 도로를 통과하거나 고르지 않은 도로에서 다른 속도로 차량을 운전하여 도출 할 수 있다. 그러나 본 연구에서는 고성능 레이저 스캐너와 센서 모듈의 출력을 ICP(Iterative Closest Point)16)로 비교함으로 얻도록 한다. 본 알고리즘으로 두 센서 출력간의 축척과 편차를 얻을 수 있다.
이 모든 알고리즘은 초음파 송신기의 하드웨어적인 반복 송신 한계로 12 ms 주기로 실행되며, 차량과 노면 사이의 거리는 각 주기마다 계산된다. 초음파 수신 후 모든 계산은 1 ms 내로 완료되고, 가공된 노면과의 거리 정보와 종방향 위치차는 현가장치 제어기로 전달된다.
5. 실외 실험과 결과
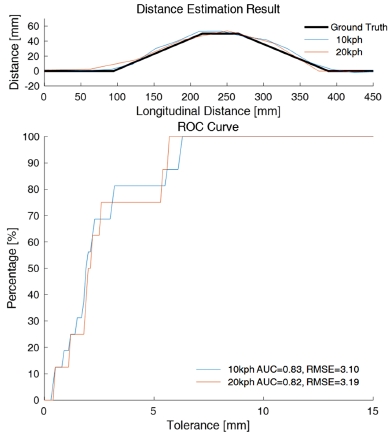
앞에서 제안한 내용들을 검증하기 위해 실외의 실차 환경에서 실험을 수행한다. 실제 노면의 높이를 측정하기 위해 Photo. 1처럼 능동 현가장치가 장착된 대형 세단인 Genesis BH 모델의 앞바퀴 앞에 초음파 센서 모듈뿐만 아니라 고성능 레이저 스캐너도 차량에 장착한다. 본 실험에 사용한 레이저 스캐너의 정확도는 수십 um 이내이며 도로 표면을 초당 수천 번 2차원으로 스캔한다. 차량은 노란색 범프를 일정한 속도로 통과하며 초음파 센서 모듈의 추정치와 레이저 스캐너의 출력을 비교한다. 지나갈 범프의 길이는 290 mm이며, 높이는 50 mm이다.
실외 실험 결과는 Fig. 6과 같다. 그림에서 ROC (Receiver Operating Characteristic)는 해당 허용 오차 내에 있는 추정 점의 총 양에 대한 비율을 나타내므로 100 %에 위치할수록 성능이 좋고, AUC(Area Under Curve)는 ROC로 생성된 면적의 비율이다. 즉, AUC 값이 1에 가까울수록 추정 성능이 좋다고 할 수 있다.
노면의 높이 추정 결과를 보면 평지 부분보다, 가정이 벗어나게 되는 경사 부분이 오차가 다소 큰 것을 확인 할 수 있다. 하지만 평균 제곱근 오차는 3.5 mm 이내로 다소 신뢰할만한 결과를 얻었다.
6. 결 론
본 논문에서는 비용이 비싸고 많은 계산량을 필요로 하는 라이다 및 스테레오 카메라 모듈을 대체하기 위해 초음파 예견 센서 모듈을 제안하였다. 초음파 예견 센서 모듈 개발을 위해 대량생산에 적합한 하드웨어 및 임계 값 기반 노면 추정 알고리즘을 제안하였고 노면과 센서간의 관계를 모델링하고 근사시킴으로 주변 잡음에 강인한 추정 알고리즘을 제안하였다. 또한 시뮬레이션으로 모델링된 식의 성능을 확인하였고, 야외에서의 실차 실험으로 센서 모듈의 사용 가능성을 확인하였다.
실제로 노이즈가 없는 환경에서 근사식인 da의 성능은 모델링 된 dm의 성능보다 약간 낮지만, dm의 경우 모든 초음파 수신기가 정확한 측정을 수행해야 정확한 노면 높이를 추정할 수 있었다. 그러나 da는 각 수신기마다 독립적으로 노면 높이 추정이 가능하여 주변 잡음이 존재하는 상황에서도 후처리를 통해 좋은 성능이 나옴을 확인할 수 있었다.
마지막으로 실외에서의 실차 실험을 통해 센서 모듈 및 알고리즘의 성능을 검증하였다. 실험 결과 실외 환경에서 평균 제곱근 오차는 4 mm 미만의 성능을 보여주었다.
또한 본 실험에서 사용한 초음파 센서 모듈은 측정한 노면이 타이어 중심에 닿기까지 20 km시 9개, 40 km시 5개, 그리고 70 km시 3개의 측정점을 얻을 수 있었다.
현재 추가적으로 본 센서 모듈에 고려가 되어야 하는 부분은 패키징 문제이다. 흙이나 먼지, 눈과 같은 장애물이 초음파 센서의 진동판을 막지 않도록 센서부를 하드웨어적으로 잘 설계해야 한다. 향후 연구는 이러한 부분을 고려한 센서 모듈로 종방향 및 횡방향 노면의 경사도를 추정하도록 한다.
Nomenclature
| d : | distance between sensor and road surface |
| b : | distance between sensors |
| α : | slope of road surface |
| v : | sound velocity |
| ttof : | time-of-flight |
| dm : | model-based distance between sensor and road surface |
| da,n : | distance between sensor and road surface for n-th receiver including assumptions |
| dn : | flight distance from transmitter to n-th receiver |
| tn : | flight time from transmitter to n-th receiver |
| tb,n : | time deviation in n-th receiver |
| db,n : | distance deviation in n-th receiver |
| ax,n : | distance correction parameters for n-th receiver |
| bx : | longitudinal position correction parameter |
Acknowledgments
본 연구는 중소기업청의 기술혁신개발사업(S23 41501, 센서기반 전동형 댐퍼 및 초고강도/초경량 소재를 이용한 승차감향상 20%, 부품 경량화 30% 가능한 차량용 능동 샤시 모듈 개발)과 미래창조과학부 및 정보통신기술진흥센터의 대학ICT연구센터육성 지원사업(IITP-2017-2012-0-00628)의 연구결과로 수행되었음.
References
-
L. Zuo, and P. -S. Zhang, “Energy Harvesting, Ride Comfort, and Road Handling of Regenerative Vehicle Suspensions”, Journal of Vibration and Acoustics, Vol.135(No.1), p011002, (2013).
[https://doi.org/10.1115/1.4007562]

-
S. Shin, and G. Choi, “Driving Performance Analysis of a Rear In-wheel Motor Vehicle with Simultaneous Control of Driving Torque and Semi-active Suspension System”, Transactions of KSAE, Vol.23(No.1), p11-17, (2015).
[https://doi.org/10.7467/ksae.2015.23.1.011]

-
I. S. Han, Y. B. Lee, K. J. Choi, J. Y. Kim, and M. E. Jang, “The NCF Algorithm for the Control of an Electro-mechanical Active Suspension System”, Transactions of KSAE, Vol.20(No.4), p1-9, (2012).
[https://doi.org/10.7467/ksae.2012.20.4.001]

-
B. L. Gysen, J. J. Paulides, J. L. Janssen, and E. A. Lomonova, “Active Electromagnetic Suspension System for Improved Vehicle Dynamics”, IEEE Transactions on Vehicular Technology, Vol.59(No.3), p1156-1163, (2010).
[https://doi.org/10.1109/tvt.2009.2038706]

-
C. Gohrle, A. Schindler, A. Wagner, and O. Sawodny, “Road Profile Estimation and Preview Control for Low-bandwidth Active Suspension Systems”, IEEE/ASME Transactions on Mechatronics, Vol.20(No.5), p2299-2310, (2015).
[https://doi.org/10.1109/tmech.2014.2375336]

- M. -H. Kim, and S. B. Choi, “Scanning Road Surface for Preview System using Ultrasonic Sensors”, KSAE Spring Conference Proceedings, p1215-1217, (2016).
-
S. Ryu, Y. Kim, and Y. Park, “Robust H∞ Preview Control of an Active Suspension System with Norm-bounded Uncertainties”, Int. J. Automotive Technology, Vol.9(No.5), p585-592, (2008).
[https://doi.org/10.1007/s12239-008-0069-7]

-
A. Jaakkola, J. Hyyppa, H. Hyyppa, and A. Kukko, “Retrieval Algorithms for Road Surface Modelling using Laser-based Mobile Mapping”, Sensors, Vol.8(No.9), p5238-5249, (2008).
[https://doi.org/10.3390/s8095238]

-
F. Oniga, and S. Nedevschi, “Processing Dense Stereo Data Using Elevation Maps: Road Surface, Traffic Isle, and Obstacle Detection”, IEEE Transactions on Vehicular Technology, Vol.59(No.3), p1172-1182, (2010).
[https://doi.org/10.1109/tvt.2009.2039718]

-
I. Maalej, M. Ouali, and N. Derbel, “Modular Ultrasonic Sensor Platform for Mobile Robot”, 2012 First International Conference on Renewable Energies and Vehicular Technology, p477-483, (2012).
[https://doi.org/10.1109/revet.2012.6195316]

- M. Kim, and S. Choi, “Road Surface Height Estimation for Preview System Using Ultrasonic Sensor Array”, FISITA World Automotive Congress, (2016).
- M. Kim, and S. Choi, “Verification of Ultrasonic Preview Sensor Module for Suspension Control”, KSAE Spring Conference Proceedings, p482-484, (2017).
-
L. Kleeman, and R. Kuc, Sonar Sensing, Springer Handbook of Robotics, Springer, p753-782, (2016).
[https://doi.org/10.1007/978-3-319-32552-1_30]

-
D. Marioli, C. Narduzzi, C. Offelli, D. Petri, E. Sardini, and A. Taroni, “Digital Time-of-flight Measurement for Ultrasonic Sensors”, IEEE Transactions on Instrumentation and Measurement, Vol.41(No.1), p93-97, (1992).
[https://doi.org/10.1109/19.126639]

-
R. Demirli, and J. Saniie, “Model-based Estimation of Ultrasonic Echoes. Part i: Analysis and algorithms”, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, Vol.48(No.3), p787-802, (2001).
[https://doi.org/10.1109/58.920713]

-
Z. Zhang, “Iterative Point Matching for Registration of Free-form Curves and Surfaces”, International Journal of Computer Vision, Vol.13(No.2), p119-152, (1994).
[https://doi.org/10.1007/bf01427149]

-
V. Agarwal, N. V. Murali, and C. Chandramouli, “A Cost-effective Ultrasonic Sensorbased Driver-assistance System for Congested Traffic Conditions”, IEEE Transactions on Intelligent Transportation Systems, Vol.10(No.3), p486-498, (2009).
[https://doi.org/10.1109/tits.2009.2026671]